Answers
Answer:
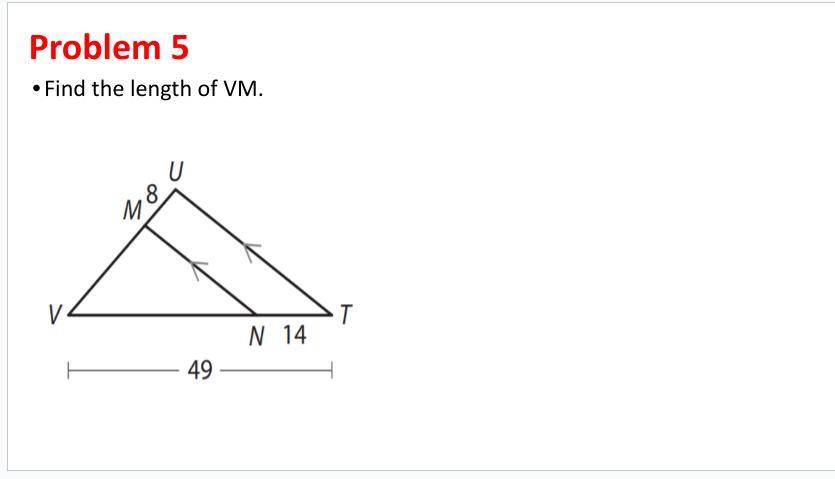
VM = 20
Step-by-step explanation:
Basic proportionality theorem or Thale's theorem:
If a line is drawn parallel to one side of a triangle to intersect the other sides in two side in distinct points, the other two sides are divided in the same ratio.
VN = VT - NT
= 49 - 14
= 35
\(\sf \dfrac{VM}{MU} = \dfrac{VN}{NT}\\\\\\\dfrac{VM}{8}=\dfrac{35}{14}\\\\\\\dfrac{VM}{8}=\dfrac{5}{2} \\\\\\VM = \dfrac{5}{2}*8\\\\VM=5*4\\\\\boxed{\bf VM = 20}\)
Related Questions
Which statement best compares the two functions?
O The minimum of function A occurs 1 unit higher than
the minimum of function B.
O The minimum of function A occurs 3 units higher
than the minimum of function B.
O The minimum of function A occurs 5 units lower than
the minimum of function B.
O The minimum of function A occurs 7 units lower than
the minimum of function B.
Answers
The two statement that best compares the two functions include the following: D. The minimum of function A occurs 7 units lower than the minimum of function B.
How to determine the true statement?By critically observing the graph of function A shown in the image attached below, we can logically deduce the following minimum value:
Minimum of function A = -2
Based on the equation representing function B, we can logically deduce that the vertex (i.e. minimum) of this function is given by the following:
y = (x + 3)² + 5
Vertex, (h, k) = (-3, 5)
This ultimately implies that, minimum value of function B is equal to 5. So, by comparison, we have:
Minimum of function = 5 - (-2)
Minimum of function = 5 + 2
Minimum of function = 7 (lower)
Read more about function here: https://brainly.com/question/27592986
#SPJ1
Complete Question:
Two different functions are shown.
Function A:
Function B: y = (x + 3)² + 5
Which statement best compares the two functions?
O The minimum of function A occurs 1 unit higher than
the minimum of function B.
O The minimum of function A occurs 3 units higher
than the minimum of function B.
O The minimum of function A occurs 5 units lower than
the minimum of function B.
O The minimum of function A occurs 7 units lower than
the minimum of function B.

Suppose you physically simulate the random process of rolling a single die. (a) After 1010 rolls of the die, you observe a "one" 44 times. What proportion of the rolls resulted in a "one"? (b) After 2020 rolls of the die, you observe a "one" 22 times. What proportion of the rolls resulted in a "one"?
Answers
Answer:
(a) 0.4 or 40%
(b) 0.1 or 10%
Step-by-step explanation:
(a) If you get 4 "ones" after 10 rolls of the die, the proportion of the rolls that resulted in "ones" is:
\(p=\frac{4}{10}\\ p=0.4\)
(b) If you get 2 "ones" after 20 rolls of the die, the proportion of the rolls that resulted in "ones" is:
\(p=\frac{2}{20}\\ p=0.1\)
What is the solution to the equation below?
8-(x+10)=2x-1
Answers
Answer:
x = -1/3
Step-by-step explanation:
1. 8-x-10 = 2x-1
2. 2x-1 = -x-2
3. 3x-1 = -2
4. 3x = -1
5. x = -1/3
8.88=-2.22(x-7)
what is x
Answers
Answer:
x=3Step-by-step explanation:
Let's solve your equation step-by-step.
8.88=−2.22(x−7)
Step 1: Simplify both sides of the equation.
8.88=−2.22(x−7)
8.88=(−2.22)(x)+(−2.22)(−7) (Distribute)
8.88=−2.22x+15.54
Step 2: Flip the equation.
−2.22x+15.54=8.88
Step 3: Subtract 15.54 from both sides.
−2.22x+15.54−15.54=8.88−15.54
−2.22x=−6.66
Step 4: Divide both sides by -2.22.
−2.22x /−2.22
=
−6.66 /−2.22
x=3
find series solution for the following differential equation. your written work should be complete (do not skip steps).y'' 2xy' 2y=0
Answers
To find the series solution for the differential equation y'' + 2xy' + 2y = 0, we can assume a power series solution of the form:
Now, substitute y(x), y'(x), and y''(x) into the differential equation:
∑(n=0 to ∞) aₙn(n-1) xⁿ⁻² + 2x ∑(n=0 to ∞) aₙn xⁿ⁻¹ + 2 ∑(n=0 to ∞) aₙxⁿ = 0
We can simplify this equation by combining the terms with the same powers of x. Let's manipulate the equation step by step:
We can combine the three summations into a single summation:
∑(n=0 to ∞) (aₙ₊₂(n+1)n + 2aₙ₊₁ + 2aₙ) xⁿ = 0
Since this equation holds for all values of x, the coefficients of the terms must be zero. Therefore, we have:
This is the recurrence relation that determines the coefficients of the power series solution To find the series solution, we can start with initial conditions. Let's assume that y(0) = y₀ and y'(0) = y'₀. This gives us the following initial terms:
To know more about a series solution:- https://brainly.com/question/31522450
#SPJ11
What does a higher mean absolute deviation mean?.
Answers
Higher mean absolute deviation is an example of a measure of variability and range. It give us some information about how spread out the data in a data set is. When used together with measures of center like the mean and median, they can give us a useful overview of the data set.
For an example,
A chef wants to hire someone to work in his kitchen. There are two candidates: Sally and Nader. To test their abilities, he times how long it takes them to make each of four meals and records the data in two tables.
He decides to calculate the mean time it took each candidate to make the four meals; he is planning to hire the candidate with the lower (quicker) mean time.
The mean time it takes Sally to make a meal is
= 3+5+7+9 / 4
=24/6
= 6 minutes
The mean time it takes Nader to make a meal is
= 5+6+5+8 / 4
=24/4
= 6 minutes
After having mean times same he doesn't classify which one is best he used their statical graphs.
For Sally, the mean absolute deviation of her times is the mean of the distances,
=4+1+2+3 / 4
=2.5
For Nader, the mean absolute deviation of his times is
= 1+0+1+2 / 4
=1
The chef sees that the mean absolute deviation of Nader’s times is lower than the mean absolute deviation of Sally’s times. This shows that Nader is more consistent in his cooking times and agrees with what we observed from the bar graphs.
Which means that the higher mean absolute deviation occurs less consistency in the mean absolute deviation.
To know more about Absolute mean deviation
https://brainly.com/question/4364130
#SPJ4
What does 3 to the zero power equal?
Answers
Answer:
1
Step-by-step explanation:
any number to the power 0 is equal to 1
Answer: 1
Step-by-step explanation:
n^0 = 1
any number raise to zero is one
Evaluate the following expression when x=2 and y= 3.6
5y2 + 3x
Answers
Answer:
Step-by-step explanation:
can somebody help me plsss

Answers
Answer:19/20
Step-by-step explanation:
a triangle has two sides of length 18 and 3. what is the largest possible whole-number length for the third side?
Answers
Answer:
20
Step-by-step explanation:
Triangle inequality says that the third side can only be 18-3...15, that is bigger than 15.
And 18+3... 21, that is smaller than 21.
If the third side is 21, the 18 and the 3 will just lay right on top of the 21 and not make a triangle. So it has to be 20 in order to be a whole number.

Write one paragraph. (10 points) 2. What is the difference geometrically between y=f(x) and z=f(x,y)? Explain with 2-3 sentences, and use examples.
Answers
Geometrically, the difference between y=f(x) and z=f(x,y) is that y=f(x) represents a two-dimensional function that can be graphed on a two-dimensional coordinate plane. The graph of the function will be a curve or a series of curves that lie on the plane.
On the other hand, z=f(x,y) represents a three-dimensional function that cannot be graphed on a two-dimensional coordinate plane. The graph of the function will be a surface that exists in three-dimensional space. For example, the equation y = x² represents a parabola that lies on the x-y plane, while the equation z = x² + y² represents a paraboloid that exists in three-dimensional space.
In mathematics, the difference between two equations can be subtle, and the same applies to geometric differences. Geometrically, the difference between y = f(x) and z = f(x, y) is that the former represents a two-dimensional function, which can be graphed on a two-dimensional coordinate plane, while the latter represents a three-dimensional function, which can be graphed on a three-dimensional coordinate system.Therefore, the graph of the two-dimensional function will be a curve or a series of curves lying on the plane. On the other hand, the graph of the three-dimensional function will be a surface that exists in three-dimensional space. Moreover, the curve has only one input, which is x, while the surface has two inputs, which are x and y. For instance, y = x² represents a parabola, which is a two-dimensional function, and lies on the x-y plane. On the other hand, z = x² + y² represents a paraboloid, which is a three-dimensional function and exists in three-dimensional space.
To know more about Geometrically visit:
https://brainly.com/question/29170212
#SPJ11
what is the volume of the solid generated when the region in the first quadrant bounded by the graph of y
Answers
The volume of the solid generated when the region in the first quadrant is: V ≈ 183.78
Volume of Solid Revolution:The disc method, the shell method, and Pappus' centroid theorem can all be used to calculate volume. In many academic disciplines, such as engineering, medical imaging, and geometry, revolution volumes are used. Integration can be used to determine the area of a region bounded by a known curve.
Because we are only revolving the region in the first quadrant, the x values range from x = 0 to x = 3.
Because of the rotation is about the vertical line x = -1, the radius of the cylindrical shell at x is r = x + 1.
The height of the cylindrical shell at x is h = \(x^{2}\)
We can now create our integral equation to find the volume:
\(V =2\pi\int\limits^a_b {rh} \, dx =2\pi\int\limits^3_0 {(1+x)x^2} \, dx \\\\V =2\pi\int\limits^3_0 {(x^{2} +x^3)} \, dx\)
We can now integrate and evaluate to find the volume of the solid.
\(V=2\pi(\frac{x^3}{3}+\frac{x^4}{4} )|^3_0\\\\V = 2\pi(\frac{27}{3}+\frac{81}{4} )\\\\V=\frac{117\pi}{2}\)
V ≈ 183.78
Learn more about Volume of the solid at:
https://brainly.com/question/30465757
#SPJ4
The given question is incomplete, complete question is:
Find the volume of the solid generated by revolving the region in the first quadrant bounded above by the curve y =\(x^{2}\), below by the x-axis, and on the right by the line x = 3, about the line x = −1
simultaneous equations
x+y=5
x squared-y squared=15
Answers
Answer:
(4,1)
Step-by-step explanation:
easiest method is to graph each equation and look for point(s) of intersection
Answer: x=4, y=1.
Step-by-step explanation:
\(\left \bigg \{ {\big{x+y=5} \atop\big {x^{2}-y^{2} =15}} \right.\\\\x+y=5\\x+y-y=5-y\\x=5-y\\\\(5-y)^{2} -y^{2} =15\\5^{2} -10y+y^{2} -y^{2}=15\\25-10y=15\\25-10y-25=15-25\\ -10y=-10\\-10y \div (-10)=-10 \div (-10)\\y=1\\\\x+y=5\\x+1=5\\x+1-1=5-1\\x=4\)
Which table of values represents the exponential function f(x) = 0.1" - 4?
a f(x)
1-1 – 14
0 -5
1 6
2 15
-1
z f(x)
-3
0 -3
1 -3.9
2 -3.9
30
- 1
0
f(x)
6
-3
-3.9
-3.99
1
2
.
2 f(a)
-4.1
0 -4
1 -3.9
2
3.99
Answers
Answer:
what did you just ask? if you explain better i can actually answer?
Step-by-step explanation:
if you have a set of data pairs that show the amount of rain for each month of the year, what type of graph would you use?
Answers
Solution
Question: Which type of graph would you use to compare the amount of rainfall each month for one year.
Answer: Line Graph
i.e Bar graph , Histogram, etc
Which function has the given properties below? The domain is the set of all real numbers. One x-intercept is (2 pi, 0). The amplitude is 4. The point (StartFraction pi over 2 EndFraction, negative 4 EndFraction) is on the graph. The y-intercept is (0, 0). Y = –4sin(x) y = –4cos(x) y = 4sin(x) y = 4cos(x).
Answers
The functions y = -4sin (x) and y = 4sin (x) has the given properties.Functions help to define the relationship between the independent and the dependent variable.
What is function?A expressions defining a connection between the independent variable and dependent variable is known as the functions.
A feature that:
The domain is defined as the set of all real numbers.
a single x-intercept
The amplitude is four.
The y-intercept is defined as (0,0)
Because the specified function goes through the functions having "cosine," the functions containing "cosine" can be omitted from the selections (0,0). As a result, we have two options:
Hence y = -4sin (x) and y = 4sin (x) has the given properties.
To learn more about the function refer to the link;
https://brainly.com/question/5245372
Answer:
A) y = -4sin(x)
Step-by-step explanation:
Just took the quiz on edge 2022

One - fourth of a number minus 8 is -23
Answers
Answer:
number is - 60
Step-by-step explanation:
let n be the number , then
\(\frac{1}{4}\) n - 8 = - 23 ( add 8 to both sides )
\(\frac{1}{4}\) n = - 15 ( multiply both sides by 4 to clear the fraction )
n = 4 × - 15 = - 60
the number n is - 60
Answer:
-60
Step-by-step explanation:
1/4x-8=-23 (Add 8 to -8 & -23)
1/4x=-15 (Divide 1/4 by each side)
-15 Divided by 1/4
X=-60
Multiplicative inverse of -3 6/11 ? In fraction form- please and thank you ^^
Answers
Answer:
Step-by-step explanation:
first you have to make this an improper fraction my multiplying -3 by 11 then add the product of that to 6 and put it all over 11
\(-3\frac{6}{11}\) → \(-\frac{39}{11}\)
once you get this you have to do the reciprocal of this to get them to equal 1
\(-\frac{39}{11}\) → \(-\frac{11}{39}\)
then multiply the number by the reciprocal
\(-\frac{39}{11}* -\frac{11}{39}=\frac{429}{429}=1\)
what is the determinant of an elementary row replacement matrix?an elementary nxn row replacement matrix is the same as the nxn identity matrix with of the replaced with some number k. this means it is and so its determinant is the of its diagonal entries. thus, the determinant of an elementary row replacement matrix is
Answers
The determinant of an elementary row replacement matrix is the product of its diagonal entries.
So if we have a matrix E with diagonal entries d1, d2, ..., dn, the determinant of E is:
determinant(E) = d1×d2×...×dn
What is an elementary row replacement matrix?An elementary row replacement matrix is a matrix that is formed by performing an operation on an identity matrix, which is nxn. Row replacement is a basic operation in linear algebra in which a row is multiplied by a scalar and then added to another row. These basic row operations are called elementary row operations.
Let's take an example to understand this more clearly. Consider the matrix given below:
[1, 3, 1][1, 0, 0][2, 2, 2]
We want to replace the third row with the first row multiplied by 2 and subtracted from the third row, the matrix would be:
[1, 3, 1][1, 0, 0][0, -4, 0]
The matrix resulting from this operation is an elementary row replacement matrix. We can see that the matrix has the form of an identity matrix with one nonzero entry. Since the determinant of an identity matrix is 1, we can also say that the determinant of an elementary row replacement matrix is the same as the determinant of the matrix resulting from the operation.To calculate the determinant of an elementary row replacement matrix, we use the formula for the determinant of a matrix. The determinant of a matrix is the sum of the products of the elements in each row and column. The formula for the determinant of an nxn matrix is:
|A| = a11 A11 + a12 A12 + ... + a1n An1
where Aij is the cofactor of the element aij. The determinant of an elementary row replacement matrix is the product of its diagonal entries.
for such more question on matrix
https://brainly.com/question/94574
#SPJ11
let f(x, y) be a function such that • the limit of f(x, y) as x → 0 along the path y = x is 0. • the limit of f(x, y) as x → 0 along the path y = x 2 is 0.
Answers
The function f(x, y) satisfies the conditions that its limit approaches zero as x approaches zero along two different paths: y = x and y = x^2. This implies that as x approaches zero, the function f(x, y) must approach zero regardless of whether y varies linearly or quadratically with x.
The given conditions state that the limit of f(x, y) as x approaches zero along the path y = x is zero. This means that as x gets arbitrarily close to zero, the function f(x, y) approaches zero when y varies linearly with x. Similarly, the second condition states that the limit of f(x, y) as x approaches zero along the path y = x^2 is also zero. This implies that when y varies quadratically with x, the function f(x, y) still approaches zero as x approaches zero. Therefore, the function f(x, y) must satisfy both conditions by converging to zero as x approaches zero along both paths.
To learn more about function click here: brainly.com/question/30721594
#SPJ11
If a ball is thrown into the air with a velocity of 40 ft/s, its height in feet after t seconds is given by y=40t−16t2.a) Find the average velocity for the time period beginning when t=2 and lasting(i) 0.5 seconds(ii) 0.1 second(iii) 0.05 seconds(iv) 0.01 secondb) Find the instantaneous velocity when t=2.
Answers
The average velocities for the given time periods has been calculated and the instantaneous velocity when t = 2 is -24 ft/s.
To find the average velocity for the given time periods, we need to calculate the change in position divided by the change in time. The formula for average velocity is:
Average Velocity = (Δy) / (Δt)
For the time period of 0.5 seconds:
Substituting t = 2 and t = 2.5 into the equation \(y = 40t - 16t^{2}\), we have:
\(y1 = 40(2) - 16(2^{2}) = 80 - 64 = 16 ft\)
\(y2 = 40(2.5) - 16(2.5^2) = 100 - 100 = 0 ft\)
Δy = y2 - y1 = 0 - 16 = -16 ft
Δt = 0.5 seconds
Average Velocity = (Δy) / (Δt) = (-16 ft) / (0.5 s) = -32 ft/s
For the time period of 0.1 seconds:
Substituting t = 2 and t = 2.1, we have:
\(y1 = 40(2) - 16(2^{2}) = 80 - 64 = 16 ft\\ y2 = 40(2.1) - 16(2.1^{2}) = 84 - 72.24 = 11.76 ft\)
Δy = y2 - y1 = 11.76 - 16 = -4.24 ft
Δt = 0.1 seconds
Average Velocity = (Δy) / (Δt) = (-4.24 ft) / (0.1 s) = -42.4 ft/s
For the time period of 0.05 seconds:
Substituting t = 2 and t = 2.05, we have:
\(y1 = 40(2) - 16(2^{2}) = 80 - 64 = 16 ft\\ y2 = 40(2.05) - 16(2.05^{2}) = 81 - 68.56 = 12.44 ft\)
Δy = y2 - y1 = 12.44 - 16 = -3.56 ft
Δt = 0.05 seconds
Average Velocity = (Δy) / (Δt) = (-3.56 ft) / (0.05 s) = -71.2 ft/s
For the time period of 0.01 seconds:
Substituting t = 2 and t = 2.01, we have:
\(y1 = 40(2) - 16(2^2) = 80 - 64 = 16 ft\\ y2 = 40(2.01) - 16(2.01^2) = 80.4 - 64.3216 = 16.0784 ft\)
Δy = y2 - y1 = 16.0784 - 16 = 0.0784 ft
Δt = 0.01 seconds
Average Velocity = (Δy) / (Δt) = (0.0784 ft) / (0.01 s) = 7.84 ft/s
To find the instantaneous velocity when t = 2, we need to calculate the derivative of the position function y(t) with respect to t.
Taking the derivative of \(y = 40t - 16t^{2}\) gives us the velocity function v(t):
\($v(t) = \frac{{d}}{{dt}} (40t - 16t^2) = 40 - 32t$\)
Substituting t = 2 into v(t), we have:
v(2) = 40 - 32(2) = 40 - 64 = -24 ft/s
Therefore, the instantaneous velocity when t = 2 is -24 ft/s.
Learn more about average velocity here:
https://brainly.com/question/28512079
#SPJ11
In Mr. Romero's auto shop class, the ratio
of boys to girls is 5:2. If there are 35 students
in the class, how many are boys?
Answers
Answer:
boys 5:2 girls
add the ratio parts together
5 + 2 = 7
divide the total number of students by the total number of parts
35/7 = 5
now multiply each part of the ratio by 5
boys 25
girls 10
there are 25 boys
4. Car dealer Lisa Kovach paid 82% of a car's options totaling $3,098. She paid 85% on a base price of $15,480.
The destination charge was $890. What is the dealer's cost?
a. $13,158.00
b. $16,588.36
c. $18,020.36
d. $19.001.20
Answers
Part (c) is the correct option i.e. The total dealer's cost is $16588.36.
What is Percentage ?
Percentage, which is a relative figure used to denote hundredths of any quantity. Since one percent (symbolised as 1%) is equal to one hundredth of something, 100 percent stands for everything, and 200 percent refers to twice the amount specified.
Given, Cost paid for car's options = 82 % $3,098 = $2540.36
Cost paid for base price = 85 % $15,480 = $13158.
Destination charge = $890
∴ The total dealer's cost will be :
= Cost paid for car's options + Cost paid for base price + Destination charge
= $2540.36 + $13158 + $890
= $16588.36.
To learn more about Percentage, visit the link given below:
https://brainly.com/question/24877689
#SPJ1
Twelve students in Mrs. Stephenson's class have brown eyes. Twenty students in the class have a lunch box. Of Mrs. Stephenson's $30$ students, what is the least possible number of students who have brown eyes and a lunch box
Answers
Answer:
Step-by-step explanation:
Since 20 students have a lunch box, 10 students don't, so 2 out of those 12 students who have brown eyes have a lunch box.
Therefore, 2 students have both.
Hope I helped :]
PROBLEM SOLVING You are flying in a hot air balloon about 1.2 miles above the ground. Find the measure of the arc that
represents the part of Earth you can see. Round your answer to the nearest tenth. (The radius of Earth is about 4000 miles)
4001.2 mi
Z
W
Y
4000 mi
Not drawn to scale
The arc measures about __
Answers
The arc degree representing the portion of Soil you'll see from the hot air balloon is around 0.0 degrees.
How to Solve the Arc Degree?To discover the degree of the arc that represents the portion of Earth you'll be able to see from the hot air balloon, you'll be able utilize the concept of trigonometry.
To begin with, we got to discover the point shaped at the center of the Soil by drawing lines from the center of the Soil to the two endpoints of the circular segment. This point will be the central point of the bend.
The tallness of the hot discuss swell over the ground shapes a right triangle with the span of the Soil as the hypotenuse and the vertical separate from the center of the Soil to the beat of the hot discuss swell as the inverse side. The radius of the Soil is around 4000 miles, and the stature of the swell is 1.2 miles.
Utilizing trigonometry, able to calculate the point θ (in radians) utilizing the equation:
θ = arcsin(opposite / hypotenuse)
θ = arcsin(1.2 / 4000)
θ ≈ 0.000286478 radians
To discover the degree of the circular segment in degrees, we will change over the point from radians to degrees:
Arc measure (in degrees) = θ * (180 / π)
Arc measure ≈ 0.000286478 * (180 / π)
Arc measure ≈ 0.0164 degrees
Adjusted to the closest tenth, the arc degree representing the portion of Soil you'll see from the hot air balloon is around 0.0 degrees.
Learn more about arc degree here: https://brainly.com/question/15815055
#SPJ1
Find the general solution of the given differential equation. (x + 1) dy + (x + 2)y = 8xe^-x y(x) = __
Give the largest interval over which the general solution is defined. (Think about the implications of any singular points. Enter your answer using interval notation.) ___
Determine whether there are any transient terms in the general solution. (Enter the transient terms as a comma-separated list; if there are none, enter NONE.)
______
Answers
The general solution of the given differential equation is y(x) = C₁e^-x + 4xe^-x. The largest interval over which the general solution is defined is (-∞, ∞). There are no transient terms in the general solution.
The differential equation given can be rearranged into the form dy/dx + (x + 2)/(x + 1)y = 8xe^-x, which is a linear first order differential equation. Using the integrating factor method, an integrating factor of e^(x + 1) can be used to obtain the general solution y(x) = C₁e^-x + 4xe^-x.
The integration constant C₁ can be determined by supplying the appropriate initial conditions. As the equation is a linear first order differential equation, the general solution is valid over the entire domain of x, which is (-∞, ∞). As the equation does not involve any terms that provide a particular value for y at any point in the domain, there are no transient terms in the general solution.
Learn more about the general solutions here:
https://brainly.com/question/2284325
#SPJ4
Diego applied to x colleges. If Nikki applied to 3 times as many colleges as Diego did, how many colleges did Nikki apply to?
3
x + 3
3x
3x + 3
Answers
Nikki applied to 3x colleges.
To determine the number of colleges Nikki applied to, we need to multiply the number of colleges Diego applied to by 3. Hence, the answer is represented by the mathematical expression 3x.
Explanation:In this problem, 'x' represents the number of colleges Diego applied to. Nikki, on the other hand, applied to 3 times as many colleges as Diego did.
So, to find out the total number of colleges Nikki applied to, we multiply the number of colleges Diego applied to ('x') by 3.
Hence, the correct mathematical expression for the number of colleges Nikki applied to would be 3x.
Learn more about Multiplication here:https://brainly.com/question/35502092
#SPJ2
Kim bought 12 boxes of drinks
He paid $15 for each box.
There were 12 drinks in each box.
Kim sold 3/4 of the drinks for $1.50 each.
He sold all of the other drinks at a reduced price.
He made an overall profit of 15%.
Work out how much Kim sold each reduced price drink for.
Answers
Answer:
The amount Kim sold each reduced price drink is $1.25 each
Step-by-step explanation:
The number of boxes of drinks Kim bought = 12 boxes
The amount Kim paid for each box = $15
The number of drinks in each box = 12 drinks
The amount Kim sild 3/4 of the drinks = $1.50 each
The amount Kim sold the remaining drinks = At a reduced rate
The amount of profit Kim made = 15%
Therefore, we have;
The total amount Kim bought the whole drinks = 12 × $15 = $180
The total number of drinks = 12 × 12 = 144 drinks
3/4 of the drinks = 3/4×144 = 108 drinks
The amount Kim sold the 108 drinks = 108 × $1.5 = $162
The amount of profit Kim made = 15%
Therefore;
(((The total amount Kim sold the whole drinks) - (The total amount Kim bought the whole drinks))/(The total amount Kim bought the whole drinks)) × 100 = Percentage profit
(((The total amount Kim sold the whole drinks) - ($180))/($180)) × 100 = 15%
The total amount Kim sold the whole drinks = 0.15×$180 + $180 = $207
The total number of the remainder of the drinks = 144 - 108 = 36 drinks
The amount Kim sold the remainder of the drinks = $207 - $162 = $45
The amount Kim sold each of the remainder of the drinks at reduced price = $45/36 = $1.25
Therefore, the amount Kim sold each reduced price drink = $1.25 each.
Yooooooo somebody answer these please.

Answers
Answer:
1. distribution property
Can somebody help me with this question will mark brainliest.

Answers
Answer: 9/12
Step-by-step explanation: