Solve. \( \frac{x}{5} + 3 = 2\)help pls!!!
Answers
3 is adding on the left, then it will subtract on the right
\(\begin{gathered} \frac{x}{5}=2-3 \\ \frac{x}{5}=-1 \end{gathered}\)5 is dividing on the left, then it will multiply on the right
\(\begin{gathered} x=(-1)\cdot5 \\ x=-5 \end{gathered}\)Related Questions
Five less than twice the sum of a number n and twelve
Answers
How to model using base 10 blocks to multiply 4x16
Answers
Answer:
Step-by-step explanation:
64
Hey can anyone help me understand how to graph this?

Answers
Answer:
Step-by-step explanation:
?
Solve for T.
need help fast please!!!

Answers
Answer:
\( \rm T = \dfrac{6 B + 4}{R} \)
Step-by-step explanation:
\( \rm Solve \: for \: T: \\ \rm \longrightarrow B = \dfrac{R T - 4}{6} \\ \\ \rm B = \dfrac{R T - 4}{6} \: is \: equivalent \: to \: \dfrac{R T - 4}{6} = B : \\ \rm \longrightarrow \dfrac{R T - 4}{6} = B \\ \\ \rm Multiply \: both \: sides \: by \: 6: \\ \rm \longrightarrow R T - 4 = 6 B \\ \\ \rm Add \: 4 \: to \: both \: sides: \\ \rm \longrightarrow R T = 6 B + 4 \\ \\ \rm Divide \: both \: sides \: by \: R: \\
\rm \longrightarrow T = \dfrac{6 B + 4}{R} \)
Factor 4x+16y using the gcf
Answers
2 x 2x=4x
2 x 8y=16y
Find the product of (3x + 4)(x - 1).
O 3x² + 7x-4
O3x² + 7x-3
O3x²-x-4
O3x²+x-4

Answers
Answer:
3x² + x - 4
Step-by-step explanation:
(3x + 4)(x - 1) =
= 3x² - 3x + 4x - 4
= 3x² + x - 4
are of a trapuiezuim
Answers
Answer:
yay girl I like it like that
In the figure below, two secants are drawn to a circle from exterior point V.
Suppose that VZ=30, VW=45, and VX=22.5. Find XY.
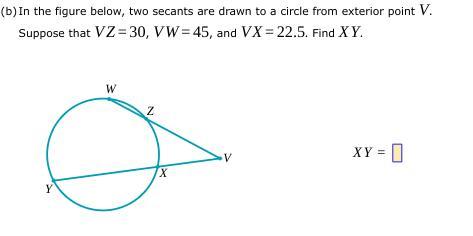
Answers
The value of secant XY is 37.5 units.
How to find the value of secant XY?The Secant-Secant Theorem states that "if two secant segments which share an endpoint outside of the circle, the product of one secant segment and its external segment is equal to the product of the other secant segment and its external segment".
Using the theorem above, we can say:
VZ * VW = VX * VY
30 * 45 = 22.5 * VY
22.5VY = 1350
VY = 1350/22.5
VY = 60 units
Since VY = VX + XY. We have:
60 = 22.5 + XY
XY = 60 - 22.5
XY = 37.5 units
Learn more about Secant-Secant Theorem on:
https://brainly.com/question/30242636
#SPJ1
Find the length of side X in simple radical form with a rational denominator
Answers
The length of side X in simple radical form with a rational denominator is 10/√3.
What is a 30-60-90 triangle?In Mathematics and Geometry, a 30-60-90 triangle is also referred to as a special right-angled triangle and it can be defined as a type of right-angled triangle whose angles are in the ratio 1:2:3 and the side lengths are in the ratio 1:√3:2.
This ultimately implies that, the length of the hypotenuse of a 30-60-90 triangle is double (twice) the length of the shorter leg (adjacent side), and the length of the longer leg (opposite side) of a 30-60-90 triangle is √3 times the length of the shorter leg (adjacent side):
Adjacent side = 5/√3
Hypotenuse, x = 2 × 5/√3
Hypotenuse, x = 10/√3.
Read more on 30-60-90 triangle here: brainly.com/question/30283450
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

what is the tan A
A 4/5
B 3/4
C 4/3
D 3/5

Answers
you can use sohcahtoa formula
sin = opposite/hypotenus
cos = adjacent/hypotenus
tan = opposite/adjacent
based on the triangle
5 = hypotenus
4 = opposite
3 = adjacent
answer : tan = 4/3
(3x + 7)
(10x – 22)
What does x equal?
Answers
Answer:
3x+7=10x-22
We simplify the equation to the form, which is simple to understand
3x+7=10x-22
We move all terms containing x to the left and all other terms to the right.
+3x-10x=-22-7
We simplify left and right side of the equation.
-7x=-29
We divide both sides of the equation by -7 to get x.
x=4.14285714286
Answer:
x=15
Step-by-step explanation:
(10x-22)+(3x+7)=180
A street sign is
73 inches tall. How tall is it in feet and inches?
Answers
Answer: 6 feet and one inch
Step-by-step explanation:
We know there are 12 inches in a foot. The nearest multiple of 12, below 73, is 72.
73 - 72 = 1 inch
72 / 12 = 6 feet
6 feet + 1 inch = 6 feet and one inch
Based on the graph how many bottles will be filled in 80 seconds? 

Answers
Answer:
Below
Step-by-step explanation:
Find unit rate (since it starts at 0,0)
at 45 seconds it is 900 bottles
900 bottles / 45 seconds = 20 bottle / sec
20 bottles / sec * 80 sec = 1600 bottles
Which graph represents the function f(x) = 2x-1 +2

Answers
Answer: Graph A
Step-by-step explanation:
Graph A. If you find the y-intercept by plugging in 0 for x, you get 2.5 = y, so therefore graph A is correct.
Round to the nearest cent 0.2745
Answers
Ten-thousandths: 0.2745
Thousandths: 0.275
hundredths: 0.27
Tenths: 0.3
In which of the following situations would it be appropriate to use a Normal distribution to approximate probabilities for a binomial distribution with the given values of n and p?
(a) n = 10, p = 0.5
(b) n = 40, p = 0.88
(c) n = 100, p = 0.2
(d) n = 100, p = 0.99
(e) n = 1000, p = 0.003
Answers
Answer:
(c) n = 100, p = 0.2
Step-by-step explanation:
To approximate to use the normal distribution for a binomial, we need that:
\(np \geq 10, n(1-p)\geq 10\)
So, for each option
(a) n = 10, p = 0.5
\(np = 10*0.5 = 5 < 10\)
So not appropriate
(b) n = 40, p = 0.88
\(np = 40*0.88 = 35.2 > 10\)
\(n(1-p) = 40*0.12 = 4.8 < 10\)
So not appropriate.
(c) n = 100, p = 0.2
\(np = 100*0.2 = 20 > 10\)
\(n(1-p) = 100*0.8 = 80 > 10\)
So appropriate
(d) n = 100, p = 0.99
\(np = 100*0.99 = 99 > 10\)
\(n(1-p) = 100*0.01 = 1 < 10\)
So not appropriated
(e) n = 1000, p = 0.003
\(np = 1000*0.003 = 3 < 10\)
So not appropriate
A Normal distribution to approximate probabilities for a binomial distribution with the given values of n = 100 and p = 0.2.
Given that,
Normal distribution to approximate probabilities for a binomial distribution with the given values of n and p.
We have to determine,
In which of the following situations would it be appropriate to use a normal distribution to approximate probabilities for a binomial distribution with the given values of n and p.
According to the question,
Probabilities for a binomial distribution with the given values of n and p.
(a) n = 10, p = 0.5
(b) n = 40, p = 0.88
(c) n = 100, p = 0.2
(d) n = 100, p = 0.99
(e) n = 1000, p = 0.003
To approximate to use the normal distribution for a binomial is given as,
\(np\geq 10 , \ n(1-p)\geq 10\)
When n = 10 and p = 0.5,\(= np \geq 10\\\\= 10 \times 0.5 = 5<10\)
The normal distribution is less than 10 so, this not appropriate.
When n = 40 and p = 0.88,\(= n.p \geq 10\\\\= (40).(0.88) \geq 10\\\\= 35.2\geq 10\\\\Then,\\=n(1-p) = 40(1-0.88) \geq 10 \\\\= 40\times 0.12 \geq 10 = 4.8\leq 10\)
The normal distribution is less than 10 so, this not appropriate.
When n = 100 and p =0.2,\(= n.p \geq 10\\\\= (100).(0.2) \geq 10\\\\= 20\geq 10\\\\Then,\\=n(1-p) = 100(1-0.2) \geq 10 \\\\= 100\times 0.8\geq 10 = 80\geq 10\)
The normal distribution is greater than 10 so, this appropriate.
When n = 100 and p = 0.99,\(= n.p \geq 10\\\\= (100).(0.99) \geq 10\\\\= 99\geq 10\\\\Then,\\=n(1-p) = 100(1-0.99) \geq 10 \\\\= 100\times 0.01\geq 10 = 1\leq 10\)
The normal distribution is less than 10 so, this not appropriate.
When n = 1000 and p = 0.003,\(= np \geq 10\\\\= 1000 \times 0.003 = 3<10\)
The normal distribution is less than 10 so, this not appropriate.
Hence, A Normal distribution to approximate probabilities for a binomial distribution with the given values of n = 100 and p = 0.2.
To know more about Binomial Distribution click the link given below.
https://brainly.com/question/16776778
The lengths of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24cm 2
, find the perimeter of the triangle.
Answers
The perimeter of the triangle is 28 cm. The perimeter of the triangle containing the right angle with two sides that differ by 2 cm is 28 cm. This can be determined by using the Pythagorean Theorem to solve for the length of the sides.
Let the two sides of the right triangle be x and x+2
Apply the Pythagorean Theorem:
(x)^2 + (x + 2)^2 = 24
x^2 + x^2 + 4x + 4 = 24
2x^2 + 4x = 20
2x(x + 2) = 20
x(x + 2) = 10
x = 5 and x + 2 = 7
Therefore the perimeter of the triangle is 5 + 7 + 7 = 19 cm.
The perimeter of the triangle is 28 cm.
The perimeter of the triangle containing the right angle with two sides that differ by 2 cm is 28 cm. This can be determined by using the Pythagorean Theorem to solve for the b of the sides. The equation 2x(x + 2) = 20 can be used to solve for x, which is equal to 5. Therefore, the two sides of the triangle are 5 cm and 7 cm. Adding these lengths together, the perimeter of the triangle is 5 + 7 + 7 = 28 cm.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
40% of what number is 36?
Answers
40/100*36
36*100/40
=90
Given below are lease terms at the local dealership. What is the total cash
due at signing?
Terms:
• Length of lease = 18 months
• MSRP of the car = $22,750
• Purchase value of the car after lease = $16,900
• Down payment = $1800
• Monthly payment = $425
• Security deposit = $400
• Acquisition fee = $300
Answers
The total cash due at signing is $3,700 at the local dealership..
What is the addition operation?The addition operation in mathematics adds values on each side of the operator.
For example 4 + 2 = 6
The total cash due is calculated as:
Down payment: $1,800
Security deposit: $400
Acquisition fee: $300
Total: $1,800 + $400 + $300
Apply the addition operation, and we get
= $3,700
Thus, the total cash due at signing is $3,700.
Learn more about Addition operations here:
brainly.com/question/25834626
#SPJ1
Sound is measured in decibels, using the formula d=10log(p/p0) where p is the intensity of the sound and p0 is the weakest sound the human ear can hear. A horn has a decibel warning of 20. how many times more intense is this horn compared to the weakest sound heard to the human ear?
Answers
Solving the given logarithmic equation, it is found that the horn is 100 times more intense compared to the weakest sound heard to the human ear.
What is the equation for the sound in decibels?The equation is given by:
\(d = 10\log{\frac{p}{p_0}}\)
In which:
d is the intensity of the sound in decibels.p is the intensity of the sound.\(p_0\) is the weakest sound that the human ear can hear.In this problem, we have that d = 20, and we have to solve the logarithmic equation for p to find how many times more intense the sound is:
\(d = 10\log{\frac{p}{p_0}}\)
\(20 = 10\log{\frac{p}{p_0}}\)
\(\log{\frac{p}{p_0}} = 2\)
The logarithm is inverse of the function \(10^x\), hence we apply the function to both sides to find the ratio.
\(\frac{p}{p_0} = 10^2\)
\(\frac{p}{p_0} = 100\)
Hence, the horn is 100 times more intense compared to the weakest sound heard to the human ear.
More can be learned about logarithmic equations at https://brainly.com/question/236421
#SPJ1
ASAPPP!!!!
A large pizza costs $12 and each topping costs an additional $2.50.
This situation can be represented by the equation y = 12 + 2.5x, where x represents the number of toppings and y represents the total cost.
What is the total cost for 9 toppings?
-$23.50
-$14.25
-$ 34,50
-$ 22.50
Answers
Answer:
$22.50
Step-by-step explanation:
So if each topping cost 2.50 then just multiply by 9
In rhombus ABCD , m∠EAB=27∘ .
What is m∠EBC ?
Enter your answer in the box.
m∠EBC = °
Rhombus A B C D with diagonals B D and A C intersecting at E.
Answers
Answer:
63°
Step-by-step explanation:
ABCD (rhombus): AC ⊥ BD and bisect at E and same length of 4 sides
∠EBA = 90 - 27 = 63
∠EBC = ∠EAB = 63°

Levy is painting a miniature model of a World War II tank. His figure uses a 1:72 scale and is 22.5 cm
long. How many centimeters long was the actual tank?
cm
Answers
Levy is painting a miniature model of a World War II tank. His figure uses a 1:72 scale and is 22.5 cm long. The actual tank is 1620 cm long.
To determine the length of the actual tank, we need to scale up the length of the miniature model using the given scale of 1:72.
Let's denote the length of the actual tank as "x".
According to the scale, 1 cm on the miniature model represents 72 cm on the actual tank.
So, we can set up the following proportion:
1 cm (miniature model) / 72 cm (actual tank) = 22.5 cm (miniature model) / x cm (actual tank)
Cross-multiplying and solving for x, we get:
x = (72 cm * 22.5 cm) / 1 cmx = 1620 cm
The actual tank is 1620 cm long.
For more such questions on miniature model
https://brainly.com/question/14657504
#SPJ8
The owner of a factory regularly requests a graphical summary of all employees' salaries. The graphical summary of salaries is an example of
a. a sample
b. descriptive statistics
c. statistical inference
d. an experiment
Answers
The graphical summary of salaries is an example of b. descriptive statistics.
Descriptive statistics is the branch of statistics that is used to summarize, organize, and describe data. It is used to present data in a clear and meaningful way, so that patterns, relationships, and trends can be easily understood. A graphical summary of all employees' salaries, such as a histogram or a bar chart, is an example of descriptive statistics.
This graphical summary represents the entire population of employees and not a subset of it, so it's not a sample. The factory owner is not making any inferences about the population based on the data, so it's not an example of statistical inference. And this is not an experiment because no manipulation of the data was made.
Learn more about descriptive statistics here: https://brainly.com/question/10272098
#SPJ4
Which one is bigger and how do you know? 1/8 or 1/9 (Give at least two strategies) i
Answers
Answer:
1/8 is the bigger fraction
Step-by-step explanation:
When comparing fractions with different denominators, and the numerator is one, like 1/8. The one with the smaller number for the denominator is greater.
You could also compare them by finding common denominators, so for 1/8 and 1/9, a common denominator would be /63. So you would take \(\frac{1}{8}\) and multiply that by \(\frac{9}{9}\). You would then get \(\frac{9}{63}\). When you take \(\frac{1}{9}\) times \(\frac{8}{8}\) you get \(\frac{8}{63}\). So when comparing you can see that 1/8 is greater than 1/9.
Sketch an angle θ in standard position such that θ has the least possible positive measure, and the point (0,-2) is on the terminal side of θ. Then find the values of the six trignometric functions for the angle. Rationalize deniminators is applicable. Do not use a calculator.
Find sin θ, cos θ, tan θ, csc θ, sec θ, and cot θ.
If it is undefined, say undefined.
Answers
The values of the six trignometric functions for the angle are
Sinθ = Sin(3π/2) = -1Cosθ = Cos(3π/2) = 0tanθ = tan(3π/2) = undefined Cotθ = Cot(3π/2) = 0Cscθ = Csc(3π/2) = 1Secθ = Sec(3π/2) = undefinedThe above sketch an angle θ in standard position such that θ has the least possible positive measure, and the point (0,-2) is on the terminal side of θ. We have to determine the value of six
triganomertric functions at angle θ. As we see at terminal side point (0,-2) the value of angle θ = 3π/2. The six trigonometric functions are sine, cosine , secant , cosecant , tangent , cotangent .
Now, Sinθ = Sin(3π/2) = Sin( π + π/2)= Sin ( 180° + π/2) = - sin(π/2) ( since, 180° + θ represents 3rd quadrant where sinθ is negative)
=> Sinθ = - 1
Cosθ = Cos(3π/2) = Cos( π + π/2)= Cos( 180° + π/2) = - Cos(π/2) ( since, 180° + θ represents 3rd quadrant where cosθ is negative)
=> Cosθ = Cos(π/2) = 0
tanθ = tan (3π/2) = tan( π + π/2)= tan( 180° + π/2) = - tan(π/2) ( since, 180° + θ represents 3rd quadrant where tanθ is positive)
=> tanθ = - sin(π/2)/cos(π/2) = 1/0
= undefined
Cscθ = Csc(3π/2) = Csc( π + π/2)= Csc( 180° + π/2) = - Csc(π/2) ( since, 180° + θ represents 3rd quadrant where cscθ is negative)
=> Cscθ = - Csc (π/2) = - 1/sin(π/2) = 1
Secθ = Sec(3π/2) = Se( π + π/2)= Sec( 180° + π/2) = - Sec(π/2) ( since, 180° + θ represents 3rd quadrant where secθ is negative)
=> Secθ = -Sec(π/2) = -1/cos(π/2) = - 1/0
= undefined
Cotθ = Cot(3π/2) = Cot( π + π/2)= Cot( 180° + π/2) = Cot(π/2) ( since, 180° + θ represents 3rd quadrant where cotθ is positive)
=> Cotθ = cot(π/2) = Cos(π/2)/sin(π/2) = 0
Hence, we determined all required triganomertric functions value for θ=3π/2.
To learn more about Trigonometric functions, refer:
https://brainly.com/question/25618616
#SPJ4

The six trignometric functions' values for the angle are
Tan = tan(3/2) = undefined, Sin = Sin(3/2) = -1, Cos = Cos(3/2) = 0, and vice versa.
Cot = Cot(3/2), Csc = Csc(3/2), and Sec = Sec(3/2), respectively.
The above drawing shows an angle in standard position with the point (0,-2) on the angle's terminal side and the smallest positive measure achievable. We must calculate the value of six.
Triganomertric operates at an angle. As can be seen, the angle's value is 3/2 at the terminal side point (0,-2). In trigonometry, there are six different functions: sine, cosine, secant, cosecant, tangent, and cotangent.
At this point, Sin = Sin(3/2) = Sin( + /2)
= Sin ( 180° + π/2) Since 180° + denotes the third quadrant, where sin is negative, the expression is equal to - sin(/2).
=> Sinθ = - 1
Cos is equal to Cos(3/2) = Cos(+/2)
because 180 degrees, = Cos(180° + /2) = - Cos(/2)
Since 180° + denotes the third quadrant, where cos is negative, the equation is Cos(180° + /2) = - Cos(/2).
Hence, Cos = Cos(/2) = 0.
Tan is equal to Tan (3/2) = Tan (+/2)
= tan( 180° + π/2) Since 180° + denotes the third quadrant, where tan is positive, the expression is = - tan(/2).
Consequently, tan = - sin(/2)/cos(/2) = 1/0
not defined
Csc is equal to Csc(3/2) = Csc(+/2)
Since 180° + represents the third quadrant, where csc is negative, Csc(180° + /2) = - Csc(/2)
=> 1/sin(/2) = 1 = Csc = - Csc (/2)
Se( + /2) = Se( = Sec(3/2)
Since 180° + represents the third quadrant, where sec is negative, sec(180° + /2) = - Sec(/2)
The formula is: Sec = -Sec(/2) = -1/cos(/2) = -1/0.
not defined
Cot = Cot(3/2), which equals Cot(+/2)
Since 180° + denotes the third quadrant, where cot is positive, the equation is Cot(180° + /2) = Cot(/2).
Consequently, Cot = Cot(2/2) = Cos(2/2)/sin(2/2) = 0
As a result, we calculated the values for all necessary triganomertric functions for 3/2.
For such more question on trignometric
https://brainly.com/question/24349828
#SPJ4
Angles in a Triangle
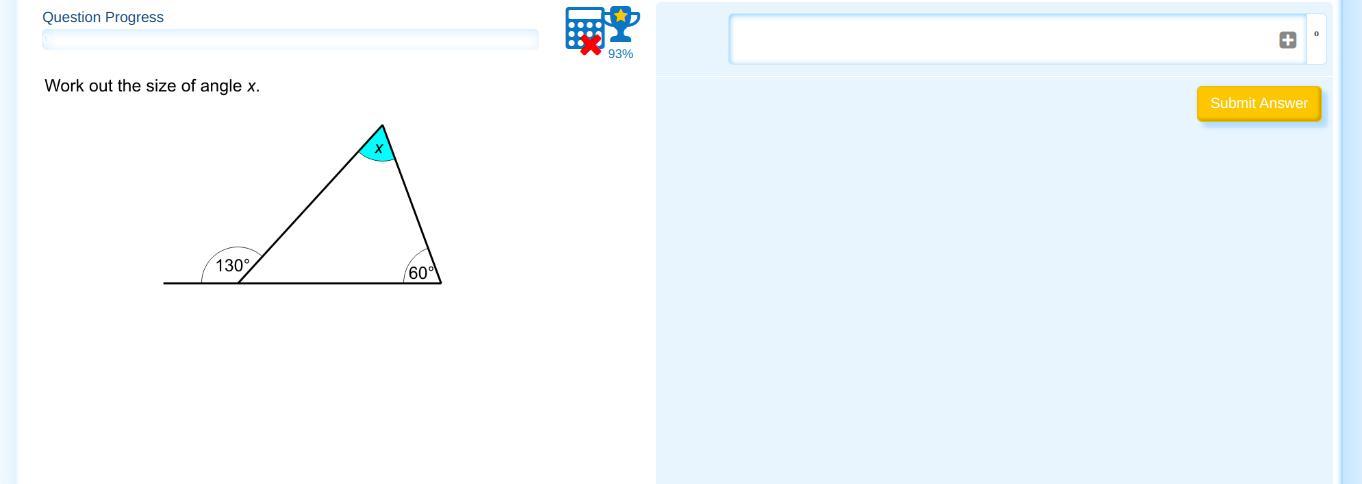
Answers
Answer:
70
Step-by-step explanation:
The non-labeled side (next to 130) has to be supplementary to the angle outside, hence it has to be 50. Since all the sides of an angle must add up to 180, we can subtract 60+50 to get 70. Hope this helps!
Answer:
70°
Step-by-step explanation:
Theorem:
The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
130 = x + 60
x = 70
Answer: 70°
Given f(x) = 52x, evaluate f-1), f(o), and K2).
01/25, 1, 625
Answers
Answer:
\(f(-1) = \frac{5}{2}\)
\(f(0) = 5\)
\(f(2) = 20\)
Step-by-step explanation:
Given
\(f(x) = 5(2^x)\)
Required
Determine f(-1); f(0) and f(2)
Solving f(-1)
In this case, we simply take x as;
\(x = -1\)
Substitute -1 for x in \(f(x) = 5(2^x)\)
\(f(-1) = 5(2^{-1})\)
Apply law of indices
\(f(-1) = 5 * \frac{1}{2}\)
\(f(-1) = \frac{5}{2}\)
Solving f(0)
In this case, we simply take x as;
\(x = 0\)
Substitute 0 for x in \(f(x) = 5(2^x)\)
\(f(0) = 5(2^0)\)
\(f(0) = 5(1)\)
\(f(0) = 5\)
Solving f(2)
In this case, we simply take x as;
\(x = 2\)
Substitute 2 for x in \(f(x) = 5(2^x)\)
\(f(2) = 5(2^2)\)
\(f(2) = 5(4)\)
\(f(2) = 20\)
The parent function for the graph to the right is of the form y = ab*. Write the parent function. Then write a function for the translation indicated
translation: right 9 units, up 3 units
Answers
Are there other rectangles that have an area of 8 cm2 but have different dimensions than the one shown? Explain how you know. Hint: What are the factors of 8?
Answers
Remember that the formula of the area of a rectangle is
\(A=lw\)Where l is the length and w is the width.
Then, we need to find all the possible pairs of numbers l and w such that
\(\begin{gathered} A=8 \\ \Rightarrow lw=8 \end{gathered}\)The case given by the problem is 2*4=8 but there are many more, for example
\(\begin{gathered} l=1 \\ \Rightarrow1\cdot w=8 \\ \Rightarrow w=8 \\ \Rightarrow(l,w)=(1,8) \end{gathered}\)Or even
\(\begin{gathered} l=3 \\ \Rightarrow3w=8 \\ \Rightarrow w=\frac{8}{3}=2.6666\ldots \end{gathered}\)There are infinite rectangles with areas equal to 8cm^2