Answers
Answer:
hope it's helpful for you

Related Questions
How can you prove the triangle sum theorem?
Answers
The sum of angle in a triangle is 180°
What is the sum of angle in a triangle?A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted \triangle ABC.
The sum of angle A, B and C is 180 i.e A+B +C = 180°
Also a triangle is a 3 sided polygon. The sum of of angle in a polygon is( n-2)180
How do we prove that the sum of angle in a triangle is 180°?
Since triangle is 3 sided, n= 3, because n denote the number if sides
therefore the sum of angle = (n-2) 180 = (3-2)×180
= 180°
therefore the sum of angle In a triangle is 180°
learn more about sum of angle In a triangle from
https://brainly.com/question/25215131
#SPJ1
A constant volume of pizza dough is formed into a cylinder with a relatively small height and large radius. The dough is spun and tossed into the air in such a way that the height of the dough decreases as the radius increases, but it retains its cylindrical shape. At time t=k, the height of the dough is 13 inch, the radius of the dough is 12 inches, and the radius of the dough is increasing at a rate of 2 inches per minute.
(a) At time t=k, at what rate is the area of the circular surface of the dough increasing with respect to time? Show the computations that lead to your answer. Indicate units of measure.
(b) At time t=k, at what rate is the height of the dough decreasing with respect to time? Show the computations that lead to your answer. Indicate units of measure. (The volume V of a cylinder with radius r and height h is given by V=πr2h.)
(c) Write an expression for the rate of change of the height of the dough with respect to the radius of the dough in terms of height h and radius r.
Answers
Answer:
a) \(\frac{dA}{dt} = 48 \pi\frac{in^{2}}{min}\)
b) \( \frac{dh}{dt} = - \frac{13}{3} \frac{in}{min}\)
c) \(\frac{dh}{dt} = - 2\frac{h}{r} \frac {dr}{dt}\)
Step-by-step explanation:
In order to solve this problem, we must first picture a cylinder of height h and radius r (see attached picture).
a) So, in order to find the rate at which the area of the circular surface of the dough is increasing with respect to time, we need to start by using the are formula for a circle:
\(A=\pi r^{2}\)
So, to find the rate of change of the area, we can now take the derivative of this formula with respect to the radius r:
\(dA = \pi(2) r dr\)
and divide both sides into dt so we get:
\(\frac{dA}{dr} = 2\pi r \frac{dr}{dt}\)
and now we can substitute:
\(\frac{dA}{dr} = 2\pi(12in)(2\frac{in}{min})\)
\(\frac{dA}{dt} = 48\pi\frac{in^{2}}{min}\)
b) In order to solve part b, we can start with the formula for the volume:
\(V=\pi r^{2} h\)
and solve the equation for h, so we get:
\(h=\frac{V}{\pi r^{2}}\)
So now we can rewrite the equation so we get:
\(h=\frac{V}{\pi}r^{-2}\)
and now we can take its derivative so we get:
\(dh=\frac{V}{\pi} (-2) r^{-3} dr\)
we can rewrite the derivative so we get:
\(\frac{dh}{dt}=-2\frac{V}{\pi r^{3}}\frac{dr}{dt}\)
we can take the original volume formula and substitute it into our current derivative, so we get:
\(\frac{dh}{dt}= -2\frac{\pi r^{2} h}{\pi r^{3}} \frac{dr}{dt}\)
and simplify:
\(\frac{dh}{dt} =-2\frac{h}{r} \frac{dr}{dt}\)
so now we can go ahead and substitute the values provided by the problem:
\(\frac{dh}{dt} =-2\frac{13in}{12in} (2\frac{in}{min})\)
Which simplifies to:
\( \frac{dh}{dt} = - \frac{13}{3} \frac{in}{min}\)
c)
Part c was explained as part of part b where we got the expression for the rate of change of the height of the dough with respect to the radius of the dough in terms of the height h and the radius r:
\(\frac{dh}{dt} =-2\frac{h}{r} \frac{dr}{dt}\)

The rate of change of the height of the pizza with respect to (w.r.t.) time
can be found given that the volume of the pizza is constant.
(a) The rate of increase of the surface area with time is 4·π in.²/min(b) The rate at which the height of the dough is decreasing is \(\underline{4.\overline 3 \ in./min}\)(c) Rate of change the height of the dough with respect to the radius \(\dfrac{dh}{dr}\), is \(\underline{-2 \cdot \dfrac{h}{r}}\)Reasons:
The height of the dough when t = k is 13 inches
Radius of the dough = 12 inches
Rate at which the radius of the dough is increasing, \(\dfrac{dr}{dt}\) = 2 in.²/min
(a) Required: The rate of increase of the surface area with time
Solution:
The circular surface area, A = π·r²
By chain rule of differentiation, we have;
\(\dfrac{dA}{dt} = \mathbf{\dfrac{dA}{dr} \times \dfrac{dr}{dt}}\)
\(\dfrac{dA}{dt} = \dfrac{d ( \pi \cdot r^2)}{dr} \times \dfrac{dr}{dt} = 2 \cdot \pi \times 2 = 4 \cdot \pi\)
The rate of increase of the surface area with time, \(\mathbf{\dfrac{dA}{dt}}\) = 4·π in.²/min.
(b) Required: The rate of decrease of the height with respect to time
The volume of the pizza is constant, given by; V = π·r² ·h
Therefore;
\(h = \mathbf{ \dfrac{V}{\pi \cdot r^2}}\)
\(\dfrac{dh}{dt} = \dfrac{d \left( \dfrac{V}{\pi \cdot r^2} \right)}{dr} \times \dfrac{dr}{dt} = \dfrac{-2 \cdot V}{\pi \cdot r^3} = \dfrac{-2 \cdot \pi \cdot r^2 \cdot h}{\pi \cdot r^3} \times \dfrac{dr}{dt} = \mathbf{-2 \cdot \dfrac{h}{r} \times \dfrac{dr}{dt}}\)
\(\dfrac{dh}{dt} = -2 \cdot \dfrac{h}{r} \times \dfrac{dr}{dt} = -2 \times \dfrac{13}{12} \times 2 = \dfrac{13}{3} = 4. \overline 3\)
The rate at which the height of the dough is decreasing, \(\mathbf{\dfrac{dh}{dt}}\)= \(\underline{4.\overline 3 \ in./min}\)
(c) Required:]The expression for the rate of change the height of the dough with respect to the radius of the cone.
Solution:
\(\dfrac{dh}{dr} = \dfrac{d \left( \dfrac{V}{\pi \cdot r^2} \right)}{dr} = \dfrac{-2 \cdot V}{\pi \cdot r^3} = \dfrac{-2 \cdot \pi \cdot r^2 \cdot h}{\pi \cdot r^3} = -2 \cdot \dfrac{h}{r}\)
\(\dfrac{dh}{dr} = \mathbf{ -2 \cdot \dfrac{h}{r}}\)
The rate of change the height of the dough w.r.t. the radius is \(\underline{\dfrac{dh}{dr} = -2 \cdot \dfrac{h}{r}}\)
Learn more here:
https://brainly.com/question/20489729
Elena is making an open-top box by cutting squares out of the corners of a piece of paper that is 11 inches wide and 17 inches long, and then folding up the sides. If the side lengths of her square cutouts are inches, then the volume of the box is given by V(x)=(11-2x)(17-2x).
There are 4 questions in the bottom! Please solve and explain them for me!
Thank youuu
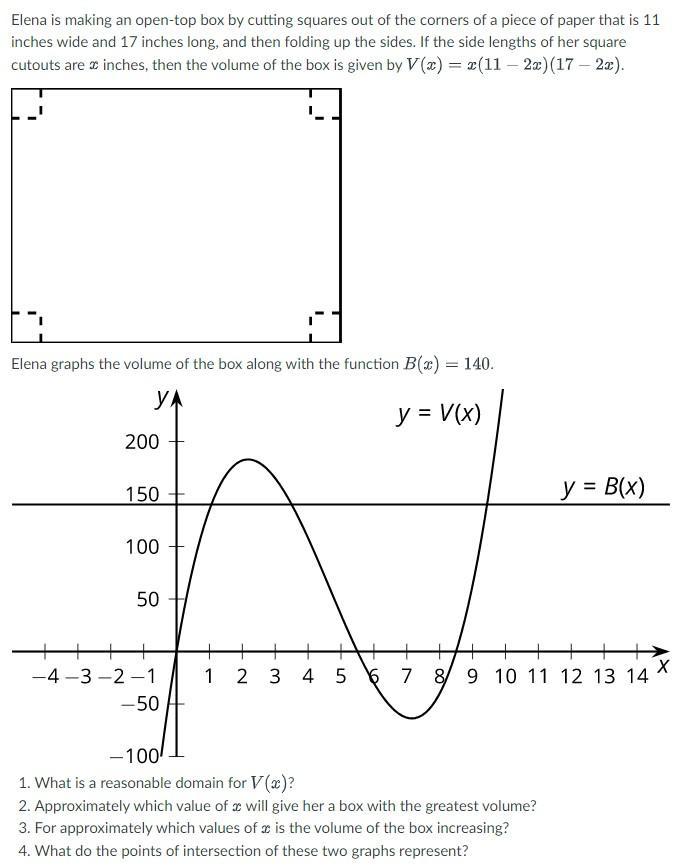
Answers
See below for the solution to each question
The reasonable domain of V(x)From the graph, we can see that:
V(x) have a positive value from x > 0 to x < 5.5
When x = 0 and ≥ 5.5, the values of V(x) are either 0 or negative
Hence, the reasonable domain of V(x) is 0 < x < 5.5
The value of x that gives the maximum volumeFrom the graph, the maximum value of V(x) is at
V(2) = 182
Hence, the approximate value of x that gives the maximum volume is 2
The values of x where the volume increasesThis is the interval where V(x) increase as x increase
From the graph, V(x) increase from x > 0 to x = 2
Hence, the approximate values of x where the volume increases are 0 < x ≤ 2
The interpretation of the point of intersectionThe other function is
B(x) = 140
So, the point of intersection represent where the volume is 140
Read more about volume function at:
https://brainly.com/question/10373132
#SPJ1
-Mutpliy
-combine like terms
-put awnser into form of a trinomial

Answers
Explanation:
1.
(x + 6)(x + 4)
= x^2 + 4x + 6x + 24
= x^2 + 10x + 24
2.
(y - 9)(y+2)
= y^2 + 2y - 9y - 18
= y^2 - 7y - 18
3.
(m + 7)(m - 5)
= m^2 - 5m + 7m - 35
= m^2 + 2m - 35
4.
(2x + 3)(4x + 1)
= 8x^2 + 2x + 12x + 3
= 8x^2 + 14x + 3
5.
(4y - 5)(y + 4)
= 4y^2 + 16y - 5y - 20
= 4y^2 + 11y - 20
50 points for this helpppp plzz

Answers
Answer:
ok
Step-by-step explanation:
Answer:
srry I needed the points hope u don\t mind
Step-by-step explanation:
Find two integers whose sum is 0 and product is -16
Answers
Answer:
the equation is x^2-16
Step-by-step explanation:
sum:0=+4-4
product:-16=+4*-4
(x-4)(x+4)
when you open the brackets the equation you will obtain will be x^2-16
The two integers whose sum is 0 and product is -16 are 4 and -4 and this can be determined by using the arithmetic operations.
Given :
Two integers whose sum is 0 and the product is -16.
The following steps can be used to determine the two unknown integers:
Step 1 - Let the two unknown integers be 'a' and 'b'.
Step 2 - According to the given data, the sum of two integers is 0 that is:
a + b = 0
a = -b --- (1)
Step 3 - Also it is given that the product of the two integers is -16 that is:
ab = -16 --- (2)
Step 4 - Substitute the value of 'a' in equation (2).
\(\rm b^2= 16\)
b = 4
Step 5 - Substitute the value of b in equation (1).
a = -4
The two integers whose sum is 0 and product is -16 are 4 and -4.
For more information, refer to the link given below:
https://brainly.com/question/1957976
Plot the points (-8, 7) and (5, 7) on the coordinate plane below.
What is the distance between these two points?
units
Answers
Therefore, the distance between the two points is 13 units.
What is distance?Distance is the measure of the length between two points or objects. It is the amount of space between two points, or the length of a path traveled by an object. Distance is typically measured in units such as meters, kilometers, miles, feet, or yards. In physics, distance is often used to describe the separation between two objects in space, and it is an important factor in many scientific calculations, such as speed, velocity,
and acceleration.
by the question.
Here is the plot of the two points on the coordinate plane:
The first point (-8, 7) is plotted 8 units to the left of the y-axis and 7 units above the x-axis. The second point (5, 7) is plotted 5 units to the right of the y-axis and 7 units above the x-axis.
To find the distance between these two points, we can use the distance formula:
\(distance =\sqrt((x2 - x1)^2 + (y2 - y1)^2)\)
where?\((x_1, y_1)\)and \((x_2, y_2)\) are the coordinates of the two points.
Plugging in the coordinates, we get:
\(distance = \sqrt((5 - (-8))^2 + (7 - 7)^2)\)
= \(\sqrt((13)^2 + (0)^2)\)
= \(\sqrt(169)\)
= 13
To learn more about distance:
https://brainly.com/question/15172156
#SPJ1

X = odd numbers less than 30
A + 3,9, 15, 21, 27
B = 5, 15, 25
(a) Complete the Venn diagram to represent this information

Answers
numerele care apartin si lui a si lui b sunt:
15
a/b={3,9,21,27}
b/a={5,25}
b)
in total sunt 15 numere impare pana la 30(cazuri posibile)
numai 7 numere apartin lui AUB(cazuri favorabile)
probabilitatea= cazuri favorabile/cazuri posibile
probabilitatea=7/15
crown?
You want to buy dome new books that cost $13 each. Shipping is $5 per order. If you but 9 books, what us the cost of the order
Answers
13(9)+5 = $122 if you buy all of the books in the same order.
$13 per book, 9 books. 13•9=117
Help!! Show your work please!

Answers
Answer:
62 degrees
Step-by-step explanation:
first we find angle C by subtracting 116 from 180
180-116
64 degrees is angle c
Sum of all three angles of a triangle is 180 degrees
(3x-13)+(2x+4)+64=180
5x-9+64=180
5x+55=180
-55. -55
5x=125
/5. /5
x=25
Now we know x we can find angle A
3(25)-13
75-13
62 degrees
Hopes this helps please mark brainliest
The exponential function f with base b is defined by f(x) = ___, b >0, and b≠1. using interval notation, the domain of this function is ____ and the range is ____
Answers
The exponential function f with base b is defined by f(x) = bˣ, b > 0, and b ≠ 1. Using interval notation, the domain of this function is (-∞, ∞) and the range is (0, ∞).
As an exponential function is defined for all real numbers, its domain is all real numbers, which can be written as (-∞, ∞), in interval notation.
Yet, the range of an exponential function is never zero.
This is due to the fact that the outcome of raising any real number to a positive power, as the exponential function does, will always be greater than 0. As a result, the exponential function with base b has a range of (0, ∞).
To learn more about domain visit:
https://brainly.com/question/1045262
#SPJ4
pls help asap!!☹️
.
.
.
.
.
.
.

Answers
Answer:
absolute value function
Step-by-step explanation:
hope this helps
22) Answer the inequality statement relating the two angles. Also please don’t answer if you don’t know it but if you do I’ll mark you as brainiest!
A) <
B) =
C) >
D) None of the above

Answers
Answer:
A) <
angle X is greater .
Step-by-step explanation:
really don't know how to...
Answer:
> im pretty sure mke sure you pay attention in class if im not correct
Step-by-step explanation:
.
Helpp plz
Both of the equations shown have the same solution when solved for x. What is the value of k? Show or explain all your work.
5x + 34 = - 2 ( 1 - 7x) and -3 ( 4x 3 ) + 4 ( 6x + 1) = k
the best answer get brainiest
Answers
Answer:
okay so its K,X (64,4)
Step-by-step explanation:
so we take any x's out that are the same or subtract them so that leaves us with only two x's and the rest are integers so we solve it from there
Find the standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin.
Vertical axis and passes through the point (?3, ?3).
Answers
The standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin is:
\(y=-\frac{1}{3}x^{2}\)
What is the equation of the parabola with a vertex at the origin and a vertical axis, which passes through the point (-3, -3)?
The equation of the parabola in standard form is \(y=-\frac{1}{3}x^{2}\). This equation represents a parabola with a vertex at the origin (0, 0) and a vertical axis. Additionally, it passes through the point (-3, -3), satisfying the given characteristics.
To find the standard form of the equation of a parabola with a vertex at the origin and a vertical axis, we can use the general equation of a parabola:
y=\(a(x-h)^{2}\)+k
where (h, k) = the vertex of the parabola.
Since the vertex is at the origin , the equation becomes:
y=a\(x^{2}\)
Now, we need to find the value of 'a' using the given point on the parabola (-3, -3).
These values are satisfied the equation, we have:
\(-3=a(-3)^2\)
Simplifying:
−3=9a
Dividing both sides by 9:
\(a=-\frac{1}{3}\)
Therefore, the standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin is:
\(y=-\frac{1}{3}x^{2}\)
Hence, the equation in standard form is:\(y=-\frac{1}{3}x^{2}\)
To learn more about the equation of the parabola from the given link
brainly.com/question/30321279
#SPJ4
statistics report that the average successful quitter is able to stop smoking after how many times?
Answers
Statistics report that the average successful quitter is able to stop smoking after multiple attempts, usually between 8 to 10 times. everyone's journey to quitting smoking is unique and may take more or fewer attempts to achieve success.
According to statistics, the average successful quitter is able to stop smoking after attempting to quit 6 to 30 times. This number varies due to individual factors and the methods used for quitting. Remember, persistence is key, and it is never too late to quit smoking for a healthier lifestyle.
learn more about statistics here:https://brainly.com/question/31538429
#SPJ11
Work out the area of the trapezium ABDE.
A
В.
7.5 cm
2.5 cm
С
5 cm
E

Answers
Answer:
Area = 50 cm²
Step-by-step explanation:
Area of a trapezium ABDE = ½(a + b)h
where,
a = BD = 2.5 cm
b = AE = 7.5 cm
h = DE = ?
We need to find DE ti be able to calculate the area.
DE = CE - CD
DE = CE - 5
Since ∆ACE is similar to ∆BCD, therefore:
AE/BD = CE/CD
Plug in the values
7.5/2.5 = CE/5
Cross multiply
CE*2.5 = 7.5*5
CE*2.5 = 37.5
Divide both side any 2.5
CE = 37.5/2.5
CE = 15
Thus, DE = CE - 5 = 15 - 5
DE = 10
✅Area of trapezium = ½(BD + AE)DE
= ½(2.5 + 7.5)*10
= ½(10)10
= 50 cm²
the formula t=((sqrt(h))/(4)) represents the time t in seconds that is takes an object to fall from a height of h feet , if a rock falls from 125 feet , estimate how long it will take the rock to hit the ground , estimate the square root to the nearest integer .
Answers
The time taken by the rock to hit the ground is 3 seconds.
It is given in the question that:-
\(t=\frac{\sqrt{h} }{4}\)
Where,
t represents the time (in seconds) taken by the object to reach the ground, and
h represents the height from which the object is falling
We have to find the time taken by a rock to hit the ground after falling from a height of 125 feet.
Using the formula given in the question, we can write,
\(t=\frac{\sqrt{125} }{4}=\frac{5\sqrt{5} }{4}\)
We know that,
\(\sqrt{5}\) ≈ 2.23
Hence, we can write,
t ≈ (5*2.23)/4 ≈ 2.7875 ≈ 3 seconds (estimated to nearest integer)
Hence, it takes around 3 seconds for the rock to hit the ground after falling from a height of 125 feet.
To learn more about time taken, here:-
https://brainly.com/question/16963199
#SPJ1
When testing the goodness of fit for the logistic regression model, if the obtained chi-square is less than the critical value, one would:None of the aboveAccept the alternative hypothesisAccept the null hypothesisReject the null hypothesis
Answers
When testing the goodness of fit for the logistic regression model, if the obtained chi-square is less than the critical value, one would " Accept the null hypothesis". The correct option is c.
In the goodness of fit test for the logistic regression model, the null hypothesis states that there is no significant difference between the observed and expected values. If the obtained chi-square value is less than the critical value, it means that the difference between the observed and expected values is not significant, and hence, we fail to reject the null hypothesis. Therefore, we accept the null hypothesis and conclude that the model fits the data well. On the other hand, if the obtained chi-square value is greater than the critical value, we reject the null hypothesis and conclude that the model does not fit the data well.
The correct option is c.
You can learn more about null hypothesis at
https://brainly.com/question/4436370
#SPJ11
You are measuring the surface area of a rectangle by measuring height and width with a really good ruler. The height measurement was 10.910 m ± 0.0004 m m. The width measurement was 5.747 m ± 0.004 m m.
What is the absolute uncertainty in the area of the rectangle?
What is the fractional uncertainty in the area of the rectangle?
Answers
The given height of the rectangle is 10.910 m ± 0.0004 m
The given width of the rectangle is 5.747 m ± 0.004 m
To find the absolute uncertainty in the area of the rectangle, first find the area of the rectangle.
The area of the rectangle is given by;
Area (A) = length (l) × breadth (b)
We can use the given measurements to calculate the area of the rectangle as follows;
l = height
= 10.910 m ± 0.0004 m
b = width
= 5.747 m ± 0.004 m
Area (A) = l × b
= (10.910 m ± 0.0004 m) × (5.747 m ± 0.004 m)
Area (A) = (10.910 m × 5.747 m) ± [(0.0004 m/10.910 m + 0.004 m/5.747 m) × (10.910 m × 5.747 m)]
Area (A) = (62.63217 m²) ± (0.0004 m/10.910 m + 0.004 m/5.747 m) × (62.63217 m²)
Area (A) = (62.63217 m²) ± 0.0566 m²
Therefore, the absolute uncertainty in the area of the rectangle is 0.0566 m².
The fractional uncertainty in the area of the rectangle is given by;
Fractional uncertainty = absolute uncertainty/mean value
Fractional uncertainty = 0.0566 m²/62.63217 m²
Fractional uncertainty = 0.000903.
Therefore, the fractional uncertainty in the area of the rectangle is 0.000903.
To know more about rectangle visit:
https://brainly.com/question/15019502
#SPJ11
how many integers from 1 through 999 do not have any repeated digits?
Answers
There are 648 integers from 1 through 999 that do not have any repeated digits.
To solve this problem, we can break it down into three cases:
Case 1: Single-digit numbers
There are 9 single-digit numbers (1, 2, 3, 4, 5, 6, 7, 8, 9), and all of them have no repeated digits.
Case 2: Two-digit numbers
To count the number of two-digit numbers without repeated digits, we can consider the first digit and second digit separately. For the first digit, we have 9 choices (excluding 0 and the digit chosen for the second digit). For the second digit, we have 9 choices (excluding the digit chosen for the first digit). Therefore, there are 9 x 9 = 81 two-digit numbers without repeated digits.
Case 3: Three-digit numbers
To count the number of three-digit numbers without repeated digits, we can again consider each digit separately. For the first digit, we have 9 choices (excluding 0). For the second digit, we have 9 choices (excluding the digit chosen for the first digit), and for the third digit, we have 8 choices (excluding the two digits already chosen). Therefore, there are 9 x 9 x 8 = 648 three-digit numbers without repeated digits.
Adding up the numbers from each case, we get a total of 9 + 81 + 648 = 738 numbers from 1 through 999 without repeated digits. However, we need to exclude the numbers from 100 to 199, 200 to 299, ..., 800 to 899, which each have a repeated digit (namely, the digit 1, 2, ..., or 8). There are 8 such blocks of 100 numbers, so we need to subtract 8 x 9 = 72 from our total count.
Therefore, the final answer is 738 - 72 = 666 integers from 1 through 999 that do not have any repeated digits.
To know more about integers visit:
brainly.com/question/15276410
#SPJ11
If U And V Are Orthogonal, What Is The Magnitude Of U Times V?
Answers
If U and V are orthogonal then the magnitude of U times V will be U.V = 0 or |UxV| = uv.
U and V are two orthogonal vectors.
since the angle between them is θ = 90⁰
let u and v be the magnitudes of the vectors U and V respectively.
so first dot-product: If two non-zero vectors are orthogonal than the dot product of these vectors will be zero. Dot product of two vectors is expressed by:
U.V = uv cosθ
since these vectors are orthogonal so,
U.V = uv cos90⁰ = 0
And Cross-product: Magnitude Cross product of two orthogonal vectors will be equal to product of magnitude of these vectors.
|UxV| = uv sin θ
|UxV| = uv sin 90⁰ = uv
Therefore, U.V = 0, |UxV| = uv.
To learn more about Cross-product:
https://brainly.com/question/29164170
#SPJ4
HELP ME PLEASE I'll give brainless.

Answers
Answer:
<QRP=42 degrees
Step-by-step explanation:
Since the angles are sequential, they are the same. This is because the transversal cuts across parallel lines, creating said sequential angles.
Answer:
42 degrees since QS&TV are parallel
What is the period, phase shift, amplitude, and vertical shift of:
Y=1/2sin(theta/4-2pi/3)+2
Answers
Answer:
Period = 8π
Phase shift = 2π/3
Amplitude = 1/2
Vertical shift = 2
Step-by-step explanation:
y = A sin((2π/T)θ − B) + C
where A is the amplitude,
T is the period,
B is the phase shift,
and C is the vertical shift.
y = ½ sin(¼θ − 2π/3) + 2
So A = 1/2, T = 8π, B = 2π/3, and C = 2.
Find the missing number:
√25 x √25 = 25 x?
(A) 1
(B) 5
(C) 10
(D) 25
Answers
Step-by-step explanation:
since sqrt(25)×sqrt(25) = 25, then x can be any number, because x = x in all cases. and then both sides of the equation are always equal, no matter what value we give x, as long as x is a factor in both sides.
sqrt(25)×x×sqrt(25) = 25x
is always true for every x.
if the question would be
sqrt(25)×x×sqrt(25) = 25
then the answer can only be x = 1. because for every other value of x the equality is destroyed.
A savings account earns 8% interest each year? If my initial deposit is $300, How much will I have at the end of 1 year?
Answers
Answer:
$324
Step-by-step explanation:
it earn 8% interest each year how much at the end of year 1,
to calculate this you multiply 300 by 108% = 300 x 1.08 = 324
The average tuition for a full-time under-
graduate student in a public college in 2002 was $4,790. In
2012 it was $8,240. Using the linear function model, estimate
the cost of tuition in 2018.
Answers
The estimated cost of tuition in 2018 using this linear function model is $726,430
What is the linear function?
A linear function is a mathematical function that describes a straight line. The general form of a linear function is:
y = f(x) = mx + b
To estimate the cost of tuition in 2018 using a linear function model, we can use the two given data points to find the slope and y-intercept of the line.
First, we can find the slope of the line by using the formula:
m = (y2 - y1) / (x2 - x1)
Where (x1, y1) is the data point for 2002 and (x2, y2) is the data point for 2012.
Substituting the values, we get:
m = (8,240 - 4,790) / (2012 - 2002) = 3,450 / 10 = 345
Next, we can use one of the data points and the slope to find the y-intercept of the line. Let's use the data point for 2002:
y = mx + b
4,790 = 345 * 2002 + b
b = 4,790 - 345 * 2002 = -1,015,290
So, the equation of the line is y = 345x - 1,015,290
To estimate the cost of tuition in 2018, we can substitute x = 2018 into the equation:
y = 345(2018) - 1,015,290 = 726,430
Hence, the estimated cost of tuition in 2018 using this linear function model is $726,430
To learn more about linear function, Visit
https://brainly.com/question/2248255
#SPJ1
Let f(x, y) = 1 – ¼ x² − 3y³ + xy. - (i) Find formulas for the partial derivatives fa and fy and use them to compute the equation for the tangent plane to f at the point x = 2, y = 1. (ii) Use the equation for the tangent plane to f from the previous problem to estimate the value of f(2.04, 1.03). Then compare this to the exact answer and determine the number of decimal places to which they agree.
Answers
(i) The equation for the tangent plane f(x, y) ≈ -7y + 8
(ii) The estimate (-1.21301) with the exact value (0.79)
(i) The partial derivatives of f(x, y), we differentiate f(x, y) with respect to each variable while treating the other variable as a constant.
The partial derivative with respect to x, denoted as fa (the subscript "a" represents the partial derivative with respect to x), is found by differentiating the terms involving x and treating y as a constant:
fa = d/dx (1 - 1/4 x² - 3y³ + xy)
= 0 - 1/4 × 2x - 0 + y
= -1/2 x + y
Similarly, the partial derivative with respect to y, denoted as fy, is found by differentiating the terms involving y and treating x as a constant
fy = d/dy (1 - 1/4 x² - 3y³ + xy)
= 0 - 0 - 9y² + x
= x - 9y²
To compute the equation for the tangent plane to f at the point (2, 1), we use the partial derivatives evaluated at this point
fa(2, 1) = -1/2 × 2 + 1 = 0
fy(2, 1) = 2 - 9 × 1² = -7
The equation for the tangent plane is given by:
f(x, y) ≈ f(2, 1) + fa(2, 1)(x - 2) + fy(2, 1)(y - 1)
Substituting the values, we have:
f(x, y) ≈ 1 + 0(x - 2) - 7(y - 1)
≈ 1 - 7(y - 1)
Simplifying, we get the equation for the tangent plane:
f(x, y) ≈ -7y + 8
(ii) To estimate the value of f(2.04, 1.03) using the equation for the tangent plane, we substitute x = 2.04 and y = 1.03:
f(2.04, 1.03) ≈ -7(1.03) + 8
≈ -7.21 + 8
≈ 0.79
To compare this estimate to the exact value, we evaluate f(2.04, 1.03) using the original function:
f(2.04, 1.03) = 1 - 1/4 (2.04)² - 3(1.03)³ + (2.04)(1.03)
≈ 1 - 1/4 (4.1616) - 3(1.09327) + (2.1072)
≈ 1 - 1.0404 - 3.27981 + 2.1072
≈ -1.21301
Comparing the estimate (-1.21301) with the exact value (0.79), we see that they differ significantly. The values do not agree to any decimal places.
To know more about tangent plane click here :
https://brainly.com/question/31428941
#SPJ4
not hard question i just forgot how to do it add the formula as well so i can remember plz thx

Answers
Answer:
15 female students in her sample
Step-by-step explanation:
134/1065 x 120 = 15.1
The cost of purchasing gasoline varies directly with the number of gallons purchased. Kali paid $52.90 for 23 gallons of gas. What is the direct variation equation that relates y, the cost of a gasoline purchase, to x the number of gallons?
Answers
Answer:
y = 2.3x
Step-by-step explanation:
y = kx
52.9 = 23x
52.9 ÷ 23 = x
x = 2.3
