Solve for x.
6(x - 2) = 4
Answers
Answer:
8/3
Step-by-step explanation:
6(x-2)=4
x-2=4/6
x= 8/3
Answer:
x = 8/3
Step-by-step explanation:
Use Distributive Property
6(x-2) = 4
6x -12 = 4
add 12 on both sides
6x = 16
Divide by 6
x = 8/3
In decimal form: 2.667
Related Questions
The demand for a product is given by D(x)=130e^(−0.025x), where x is the number of units sold each week and 0≤x≤90. Step 1 of 2: Find the number of units sold that will yield maximum revenue. Round your answer to the nearest whole unit.Step 2 of 2:Find the price per unit that will yield maximum revenue. Round your answer to the nearest cent.
Answers
(a) 40 unit have to be the number of units sold that will yield maximum revenue.
(b) The price per unit that will yield maximum revenue, will be $1.195.
(a) We have to find the number of units sold that will yield maximum revenue
Given demand function is
D(x)=130e^{-0.025x}
where is the number of units sold each week
Revenue function R(x) = xD(x)
R(x) = x∙130e^{-0.025x}
To find maximum revenue put,
R’(x) = 0
⇒d/dx(x∙130e^{-0.025x}) = 0
⇒130 d/dx(x∙e^{-0.025x}) = 0
⇒130[e^{-0.025x}+xe^{-0.025x} ∙(-0.025x)]=0
⇒130e^{-0.025x} ∙(1-0.025x)=0
⇒1 - 0.025x=0
⇒0.025x = 1
⇒x = 1/0.025
⇒x = 40units
R''(x) = 130d/d[x(e^{-0.025x}-0.025xe^{-0.025x} )]
R''(x) = 130[-0.025e^{-0.025x}-0.025e^{-0.025x}+0.00625xe^{-0.025x}]
R''(x)|x=40 = 130-0.025*40[0.050+0.00625*40]
R''(x)|x=40 = 130/e ∙(-0.025)
R''(x)|x=40 = (130*(-0.025))/e < 0
At x= 40 units, the revenue will maximize.
$0 units will yield maximum revenue.
(2) Now we have to find the price per unit that will yield maximum revenue.
D(x) = 130e-0.025x
D(40) = 130e^{-0.025*40}
D(40) = 130e^{-1}
D(40) = 130/e
D(40) = 47.82(in dollar)
Price per unit = d(40)/40
Price per unit = 47.82/40
Price per unit = $1.195
The price per unit that will yield maximum revenue, will be $1.195.
To learn more about to maximum revenue link is here
brainly.com/question/1332812
#SPJ4
what fraction is bigger -2/4 or -7/12
Answers
-7/12 = -0.583
-7/12 is bigger
Find an equation for the graph sketched below

Answers
The exponential function sketched is defined as follows:
y = 2(0.5)^x - 6.
How to define the exponential function?The standard definition of an exponential function is given as follows:
y = a(b)^x + c.
In which:
a + c is the value of y when x = 0.b is the rate of change.c is the asymptote.From the graph, the horizontal asymptote is of y = -6, hence the parameter c is given as follows:
c = -6.
When x = 0, y = -4, hence the parameter a is given as follows:
-4 = a - 6
a = 2.
Hence:
y = 2(b)^x - 6.
When x = -1, y = -2, hence the parameter b is given as follows:
2(b)^(-1) - 6 = -2
2/b = 4
b = 0.5.
Hence the function is of:
y = 2(0.5)^x - 6.
More can be learned about exponential functions at https://brainly.com/question/30113628
#SPJ1
12 students in a class brought their lunch to school, which was 48% of the students. How many students are in the class?
Answers
Φ1 = ∬S1 (-2u^6cos(v) - 2u^3sin(v)) du dv
= ∫(0->1) ∫(0->2π) (-2u^6cos(v) - 2u^3sin(v)) dv du
Answers
\(\begin{align}\sf\:\Phi_1 &= \iint_{S_1} (-2u^6\cos(v) - 2u^3\sin(v)) \, du \, dv \\ &= \int_{0}^{1} \int_{0}^{2\pi} (-2u^6\cos(v) - 2u^3\sin(v)) \, dv \, du \end{align} \\\)
What is the y-intercept of the quadratic function
f(x)= (- 8)(x +3)?
Answers
Answer:
-24
Step-by-step explanation:
The standard from of equation of a line is expressed as g(x) = mx+c where;
m is the slope
c is the y-intercept of the line.
Given the expression g(x)= (- 8)(x +3), rewriting in standard form first we have;
g(x)= (- 8)(x +3)
gx)= -8x - 24
On Comparing with g(x) mx+ c, we will see that;
c = -24
Hence the y-intercept of the quadratic function is -24
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
Answers
Answer:
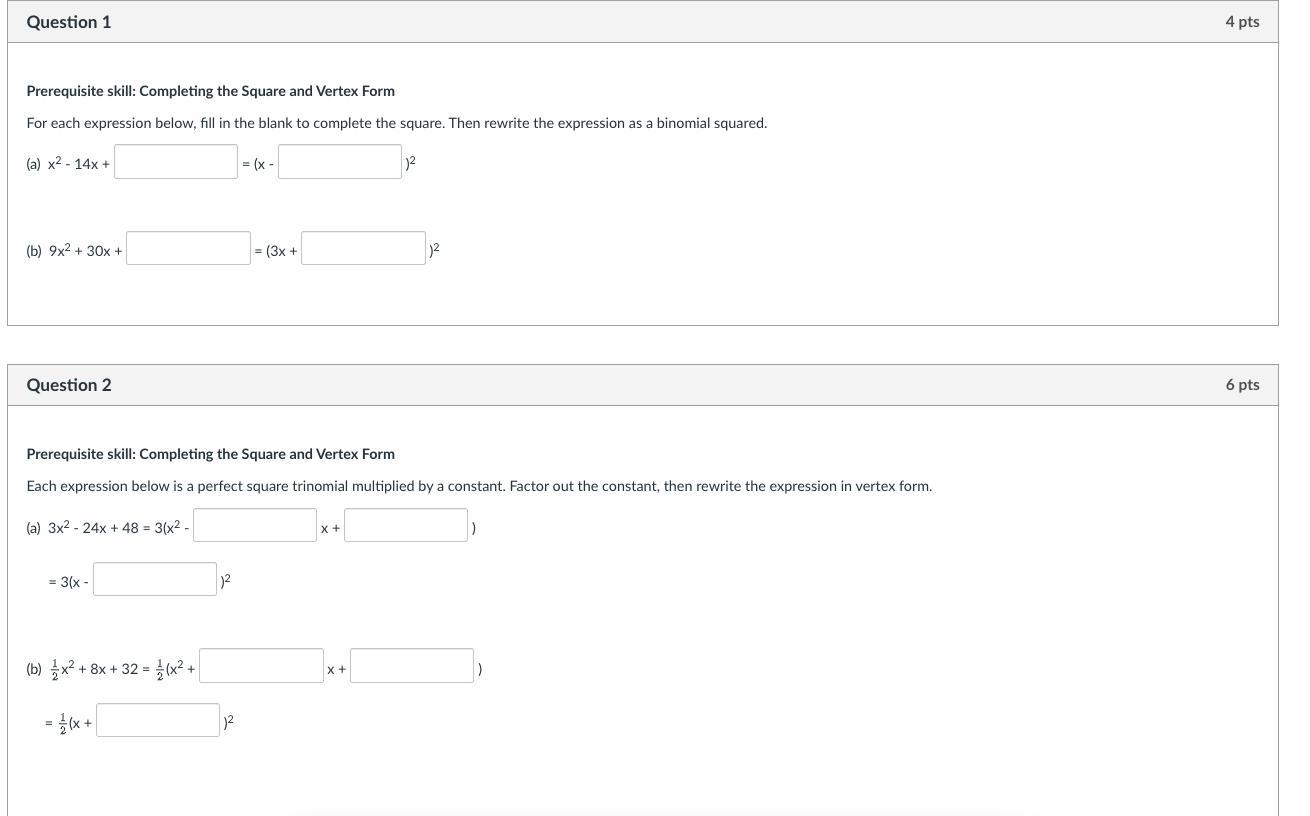
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Solve for x. Assume that lines which appear tangent are tangent.

Answers
75 units are the value of x.
If PAB is a secant to a circle intersecting it at A and B and PT is a tangent then PA.PB = PT².
In the given case,
PA = 48
PT = 60
PB = x
Thus,
60² = 48*x
x = 3600/48
x = 75
Therefore, the value of x is 75 units.
Learn more about secant here:
https://brainly.com/question/23026602
#SPJ1
An insurance office buys paper by the ream, 500 sheets, for use in the copier, fax, and printer. Each ream lasts an average of 4 days, with standard deviation 1 day. The distribution is normal, independent of previous reams. a. Find the probability that the next ream out- lasts the present one by more than 2 days. b. How many reams must be purchased if they are to last at least 60 days with probability at least 80%
Answers
Answer:
a) the probability that the next ream out- lasts the present one by more than 2 days is 0.0787
b) the number of reams that must be purchased is 19
Step-by-step explanation:
Given the data in the question;
Lets X₁ and X₂ be the two random variables that represents the first and second ream lasts
given that both random variables follow normal distribution with mean 4 and standard deviation 1.
a)
Find the probability that the next ream out- lasts the present one by more than 2 days.
P( X₂ - X₁ > 2 ) = P( [(X₂ - X₁ - E(X₂ - X₁)) / √(V(X₂ - X₁)] > [ (2-E(X₂ - X₁))/√(V(X₂ - X₁) ]
= 1 - P( Z ≤ [2-(μ₂ - μ₁)] / [√( V(X₂) + V(X₁) ) ] )
= 1 - P( Z ≤ [2-(4 - 4)] / [√( 1 + 1 )] )
= 1 - P = ( Z ≤ 2 / √2 )
= 1 - p( Z ≤ 1.4142 )
from excel; p( Z ≤ 1.41 ) = 0.9213
P( X₂ - X₁ > 2 ) = 1 - 0.9213
P( X₂ - X₁ > 2 ) = 0.0787
Therefore, the probability that the next ream out- lasts the present one by more than 2 days is 0.0787
b)
How many reams must be purchased if they are to last at least 60 days with probability at least 80%
total value is 4n
standard deviation is nσ
so
P(nX ≥ 60 ) = 0.80
P( nX-nμ /nσ ≥ 60-nμ/nσ) = 0.80
P( Z ≥ 60-4n/n) = 0.80
1 - P( Z ≥ 60-4n/n) = 0.80
P( Z < z ) = 0.20
now since z = 60-4n/n
from standard normal table
critical value of z corresponding to cumulative area of 0.20 is -0.841
so
z = - 0.841
60-4n/n = -0.841
60 - 4n = -0.841n
60 = -0.841n + 4n
60 = 3.159n
n = 60 / 3.159
n = 18.99 ≈ 19
Therefore, the number of reams that must be purchased is 19
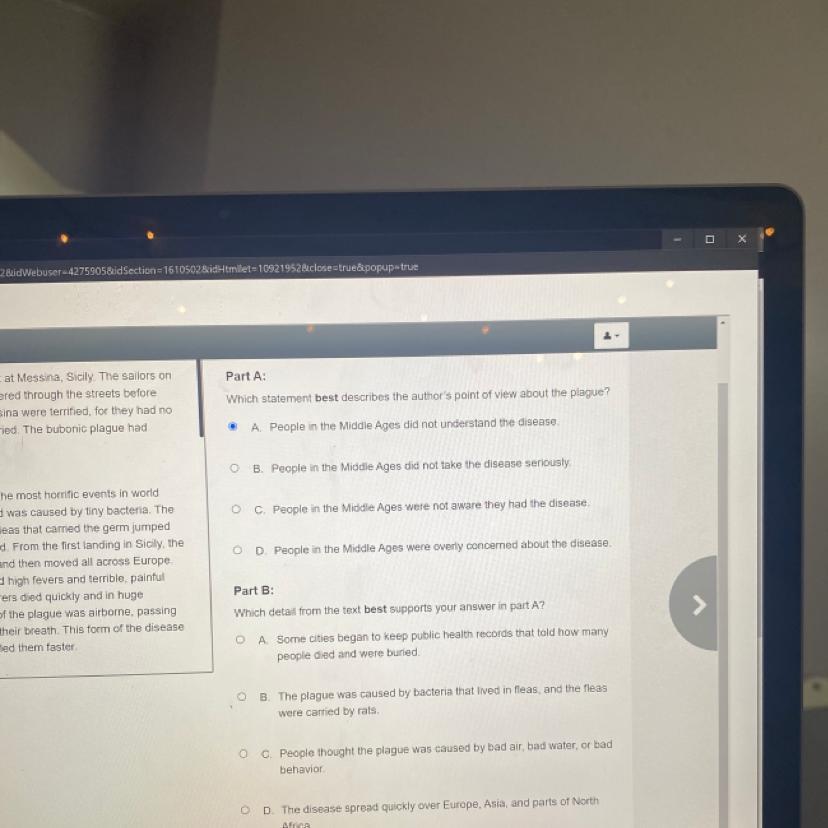
Pls answer part A and part B!!!
Answers
Answer:
22222
Step-by-step explanation:
1.67____16.7
Which is bigger
Answers
Answer:
16.7 would be the bigger
Step-by-step explanation:
Hope this helps :)
Sorry if im wrong :(
Answer:
16.7 is bigger than 1.67.
Step-by-step explanation:
Numbers have a structure, and a part of that is places. (ex. tens place, one's place, hundreds place, etc.) If you look at the numbers above, only one has a tens place. (Think about it this way; you're comparing 0 to 1 for the tens place. 1 is a larger number, so the number containing 1 in the tens place is larger) Therefore, 16.7 is larger than 1.67
Each sandbag holds 27 pounds of sand, and it takes 53 bags to go all the way around Wilma's house. How many pounds of sand does Wilma need to fill the sandbags around her house?
Answers
2.6x 0.47 pls show your work I need help
Answers
Answer:
2.6 x 0.47 = 1.222
Step-by-step explanation:
A survey of licensed drivers inquired about running red lights. One question asked, "Of every 10 motorists who run a red light, about how many do you think will be caught?" The mean result for 880 respondents was
¯x= 1.92. Suppose we know that σ = 1.83. Compute a 95% confidence interval for the mean opinion in the population of all licensed drivers. (Round your answer to the nearest hundredth.)
Answers
Answer: (0.79, 3.05 )
Step-by-step explanation:
Confidence interval for the population mean:
\(\overline{x}\pm z^c\dfrac{\sigma}{\sqrt{n}}\)
, where \(\overline{x}\) = Sample mean
\(\sigma\) = population standard deviation
n= sample size.
\(z^c\) = Critical z value for confidence interval c.
As per given:
n= 10
\(\overline{x}=1.92\)
\(\sigma=1.83\)
Critical z-value for 95% confidence = 1.96
A 95% confidence interval for the mean opinion in the population of all licensed drivers:-
\(1.92\pm (1.96)\dfrac{1.83}{\sqrt{10}}\\\\=1.92\pm1.134\\\\= (1.92-1.134,\ 1.92+1.134)\\\\\approx(0.79,\ 3.05 )\)
Hence, a 95% confidence interval for the mean opinion in the population of all licensed drivers = (0.79, 3.05)
PLEASE HELP FAST!! IT IS URGENT!! Some stores print multiple coupons and advertisements on their receipts, making the receipts unusually long. A curious shopper makes the same purchase at a random sample of 10 stores and measures the length of each receipt (n inches). Here are the results: 8.25, 7.5, 5, 9.5, 12, 5.5, 9, 14, 11.5, 18 Are the conditions for cons tructing at confidence interval met?
O No, the random condition is not met.
O No, the 10% condition is not net.
O No, the Normal/large sanple condition is not met.
O Yes, the conditions for inference are met.
Answers
Answer:
No, the Normal/large sample condition is not met. A confidence interval assumes that the underlying population follows a normal distribution and that the sample size should be at least 30. Since the sample size in this case is only 10, the Normal/Large Sample condition is not met and the conditions for constructing a confidence interval are not met.
from this part ,find the estimated y-intercept .Round your answer to the three decimal places.

Answers
y - incercept = 371.4
The table represents a linear relationship
X—2 0 4
Y-4 3 1
Which equation represents the table
Y=1/2x+5
y=-1/2x+3
Y=2x-3
Y=-4x+2
Answers
The linear relationship illustrated in the provided table can be effectively described by the equation Y = -4x + 2. Option D.
To determine the equation that represents the given table with the values of x and y, we can observe the pattern and find the equation of the line that fits these points.
Given the table:
X: 2 0 4
Y: -4 3 1
We can plot these points on a graph and see that they form a straight line.
Plotting the points (2, -4), (0, 3), and (4, 1), we can see that they lie on a line that has a negative slope.
Based on the given options, we can now evaluate each equation to see which one represents the line:
Y = 1/2x + 5
When we substitute the x-values from the table into this equation, we get the following corresponding y-values: -3, 5, and 6. These values do not match the given table, so this equation does not represent the table.
Y = -1/2x + 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: 4, 3, and 2. These values also do not match the given table, so this equation does not represent the table.
Y = 2x - 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -4, -3, and 5. These values do not match the given table, so this equation does not represent the table.
Y = -4x + 2
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -6, 2, and -14. Interestingly, these values match the y-values in the given table. Therefore, the equation Y = -4x + 2 represents the table.
In conclusion, the equation Y = -4x + 2 represents the linear relationship described by the given table. So Option D is correct.
For more question on equation visit:
https://brainly.com/question/29174899
#SPJ8
find x.
8
2radius3
8
8radius3
(hurry plz, will give brainliest) -15pts-

Answers
Answer:
Answere is X= 8
Step-by-step explanation:
Use sine law
Sin(angle) = Opposite/ Hypotenuse
Sin (30) = 4 /X
X = 4 / sin (30)
X = 8
pls help due at 11:59

Answers

Which of the following conditions are sufficient to show that triangle ABC sim triangle QPR
Select all that apply.
A. m angle Q = 63
B. m angle R = 81
D. m angle P = 81
C. RP = 4.5

Answers
Answer:
C. RP = 4.5
Step-by-step explanation:
You want to know what condition is sufficient to show ∆ABC ~ ∆QPR, given three sides and 2 angles in ∆ABC, and 2 sides in ∆QPR.
SimilaritySimilarity can be shown if all three sides are proportional, or if two angles are congruent.
The offered answer choices only list one angle, so none of those will work. The answer choice that makes the third side of ∆QPR be in the same proportion as the corresponding side of ∆ABC is the condition of interest.
C. RP = 4.5
__
Additional comment
The side ratios in the two triangles are ...
AB : BC : CA = 10 : 9 : 6
QP : PR : RQ = 5 : PR : 3
For these ratios to be the same, PR must be half of BC, just as the other segments in ∆QPR are half their counterparts in ∆ABC.
Both customers spent same amount of money. customer one bought 8 chicken wings and left a tip of four dollars. second customer bought 10 chicken wings and left a tip of $2.50. how much is each chicken wing?
Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the representation of the chicken wings
Let the chicken wing be represented by x
\(\begin{gathered} For\text{ Customer 1, he spent;} \\ 8x+4 \\ From\text{ second customer, he spent} \\ 10x+2.50 \end{gathered}\)STEP 2: Equate the two amounts
Since they both spent same amount of money, this means that;
\(8x+4=10x+2.50\)STEP 3: Solve for x
\(\begin{gathered} Collecting\text{ like terms:} \\ 8x-10x=2.50-4 \\ -2x=-1.5 \\ Divide\text{ both sides by -2} \\ \frac{-2x}{-2}=\frac{-1.5}{-2} \\ x=0.75 \end{gathered}\)Hence, each chicken wing costs $0.75
HELPPPP!!!! PLEASEEE!!!
Which statement below is true?
A. If p → q is true, then q → p is true.
B. If p → q is true and p is true, then q is true.
C. If p → q and q → r are true, then q → p is true.
D. If p → q and q → r are true, then r → p is true.
Answers
Answer: i believe the answer is B
Step-by-step explanation: because if p to q is true, then that means p and q are both true!
Circle the most precise measurement or tool in each columna scale that measures tothe nearest kg20.53 kilometers20 kilometers21 kilometers3 millimeters3.7 millimeters3.72 millimetersa scale that measures to1/10 of a kg
Answers
In the first column, 20.53 kilometer is most precise
In second column the scale that measures 1/10 of a kg is most precise.
In third column, 3.72 millimeters is precise.
For 20.53 kilometer, there are two digits after the decimal point. So, the measurement measures even the slightest change in decimals of the measurement.
1/10 of a kg can be written as 0.1 kg. So, in this scale the weight is measured upto the smallest change of one decimal point. For the scale that measures the nearest kg, the small change is not measured as there are no digits after decimal in the measurement. For example, compare the weights 500 kg and 500.5 kg . 500.5 kg is measured in 1/10 of a kg scale. The extra 0.5 kg s measure is shown. So, it will be a more precise value.
In 3.72 millimeters, there are two digits after the decimal point. So, when a measurement is taken, we get a precision upto two decimal places, while for 3.7mm, the measurement can be taken only upto one decimal place and for 3 mm no decimal points are there.
The cost of a jacket increased from $75.00 to $84.75. What is the percentage increase of the cost of the jacket?
A.
1.3%
B.
87%
C.
13%
D.
9.75%
Answers
Answer:
c) 13%
Step-by-step explanation:
Given information,
→ The cost of a jacket increased from the price $75.00 to $84.75.
Now we have to,
→ find the % increase of cost of jacket.
Let's solve the problem,
→ ((84.75 - 75)/75) × 100
→ (9.75/75) × 100
→ 0.13 × 100
→ 13%
Hence, the answer is 13%.
In a population of chickens, the average (arithmetic mean) weight is 6.3 pounds, and the standard deviation is 1.2 pounds. Which of the following weights (in pounds) are within 1.5 units of the standard deviation of the mean?
Indicate all weights.
A. 4.4
B. 4.6
C. 5.1
D. 5.2
E. 6.9
F. 7.6
G. 7.7
H. 8.2
Answers
The following weights (in pounds) are within 1.5 units of the standard deviation of the mean:
A. 4.4
B. 4.6
D. 5.2
E. 6.9
F. 7.6
The mean weight of the chickens in this population is 6.3 pounds, and the standard deviation is 1.2 pounds. To be within 1.5 units of the standard deviation, we need to look at the range of weights that are 1.2 +/- 1.5, which is 4.7 to 7.9 pounds.
This means that the weights within this range are 4.4, 4.6, 5.2, 6.9, 7.6, and any other weights that fall within the range. Therefore, the weights within 1.5 units of the standard deviation of the mean are:
A. 4.4, B. 4.6, D. 5.2, E. 6.9, and F. 7.6.
The standard deviation measures the spread of the data from the mean. In this case, the mean is 6.3 pounds and the standard deviation is 1.2 pounds. This means that the data points on either side of the mean will be 1.2 pounds away from it.
To learn more about standard deviation of the mean, use the link:
brainly.com/question/16030790
#SPJ4
While visiting Crimson lake, Sally decided to go kayaking. The rangers charge $8.50 per hour in addition to a $25 deposit to rent the kayak. If she rented the kayak from 11:30 am to 2:30 pm, write and solve a linear equation to find the total cost to rent the kayak.
Answers
Answer:
50.50$
Step-by-step explanation:
8.5x+25
x is the hours
8.5(3)+25= 50.50
Determine the measure of x in the diagram below:
x = °

Answers
The measure of angle x on the straight line is 130 degrees.
What is the measure of angle x?The sum of interior angles in a triangle equals 180 degrees.
To determine the value of x, we first determine its suplemetary angle x .
Hence:
40 + 90 + ( suplemetary angle of x ) = 180
Solve for the suplementary angle:
130 + ( suplemetary angle of x ) = 180
Suplementary angle of x = 180 - 130
Suplemetary angle of x = 50 degree
Now, we can find the measure of angle x.
Note that, sum of angles on a straight line equals 180 degree.
Hence:
x + ( suplemetary angle of x ) = 180
x + 50 = 180
Solve for x
x = 180 - 50
x = 130 degrees.
Therefore, the value of x is 130 degrees.
Learn about area of triangle here: brainly.com/question/29156501
#SPJ1
I need help!!!
What is (7×5)10÷3+6=
Answers
Answer: 38.8
Step-by-step explanation:
Step-by-step explanation:
Calculate with Parenthesis ( \(7*5\))
\(7*5=35\)
\(35*3\)÷3+6
Multiply and divide ( left to Right)
35*10/3
=350/3
350/3+6
Add and subtract (left to right):
350/3+6
=368/3
Convert improper fraction to mixed numbers:
368/3=122
Answer:
368/3=\(122 \frac{2}{3}\)
What
is an arithmetic sequence with a common difference of −2?
Answers
Answer:
An arithmetic sequence with a common difference of −2 is 20,18,16,14,12..
Step-by-step explanation:
An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is same. Here, the common difference is -2, which means that each term in the sequence is obtained by subtracting 2 from the previous term.
To find the arithmetic sequence with a common difference of -2, you can start with an first term and then subtract 2 successively to find the subsequent terms.
Let the initial term is 20. Subtracting 2 from 20, we get 18. Subtracting 2 from 18, we get 16. Continuing this pattern, we subtract 2 from each subsequent term to generate the sequence. The arithmetic sequence with a common difference of -2 starting from 20 is
20,18,16,14,12
In this sequence, each term is obtained by subtracting 2 from the previous term, resulting in a common difference of -2.
5: The US Postal Service believes less than 13% of the packages mailed during the
holiday rush are delivered late. To test this claim, it randomly selects 228 packages
during the holiday rush and finds that 24 are delivered late. Test the US Postal Service’s
claim at α = .01.
What type of error could be made based on your decision in step 5 of the above
hypothesis test?
Answers
There are two types of errors that could be made:
a Type I error and a Type II error.
We have,
In step 5 of the hypothesis test, we make a decision to either reject or fail to reject the null hypothesis.
If we reject the null hypothesis, there are two types of errors that could be made:
a Type I error and a Type II error.
A Type I error occurs when we reject a true null hypothesis.
In this context, it means that we conclude that the percentage of packages delivered late is greater than 13% when in reality it is not.
This error is also known as a false positive.
A Type II error occurs when we fail to reject a false null hypothesis.
In this context, it means that we conclude that the percentage of packages delivered late is less than or equal to 13% when in reality it is greater than 13%. This error is also known as a false negative.
The probability of making a Type I error is denoted by α, which is given in the problem statement as α = 0.01.
Therefore, if we reject the null hypothesis, there is a 1% chance that we are making a Type I error.
Thus,
The probability of making a Type II error depends on the effect size, sample size, and significance level of the test.
Learn more about hypothesis testing here:
https://brainly.com/question/30588452
#SPJ1