Solve for x
8x + 3=19
x + 4 = 11
Answers
Answer:
8x + 3 = 19
8x = 16
x = 2
x + 4 = 11
x = 7
Related Questions
Layla needs to order some new supplies for the restaurant where she works. The restaurant needs at least 643 glasses. There are currently 166 glasses. If each set on sale contains 18 glasses, write and solve an inequality which can be used to determine xx, the number of sets of glasses Layla could buy for the restaurant to have enough glasses
Answers
The inequality to determine the number of sets of glasses is
166 + 18x ≥ 643
What is inequality?It shows a relationship between two numbers or two expressions.
There are commonly used four inequalities:
Less than = <
Greater than = >
Less than and equal = ≤
Greater than and equal = ≥
We have,
Number of glasses available = 166
Number of glasses needed at the least = 643
Number of glasses in a set = 18
Now,
The number of sets of glasses to have enough glasses.
166 + 18x ≥ 643
18x ≥ 643 - 166
18x ≥ 477
x ≥ 26.5
Thus,
The number of sets of glasses required is 27.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ4
11% of a quantity is equal to
13
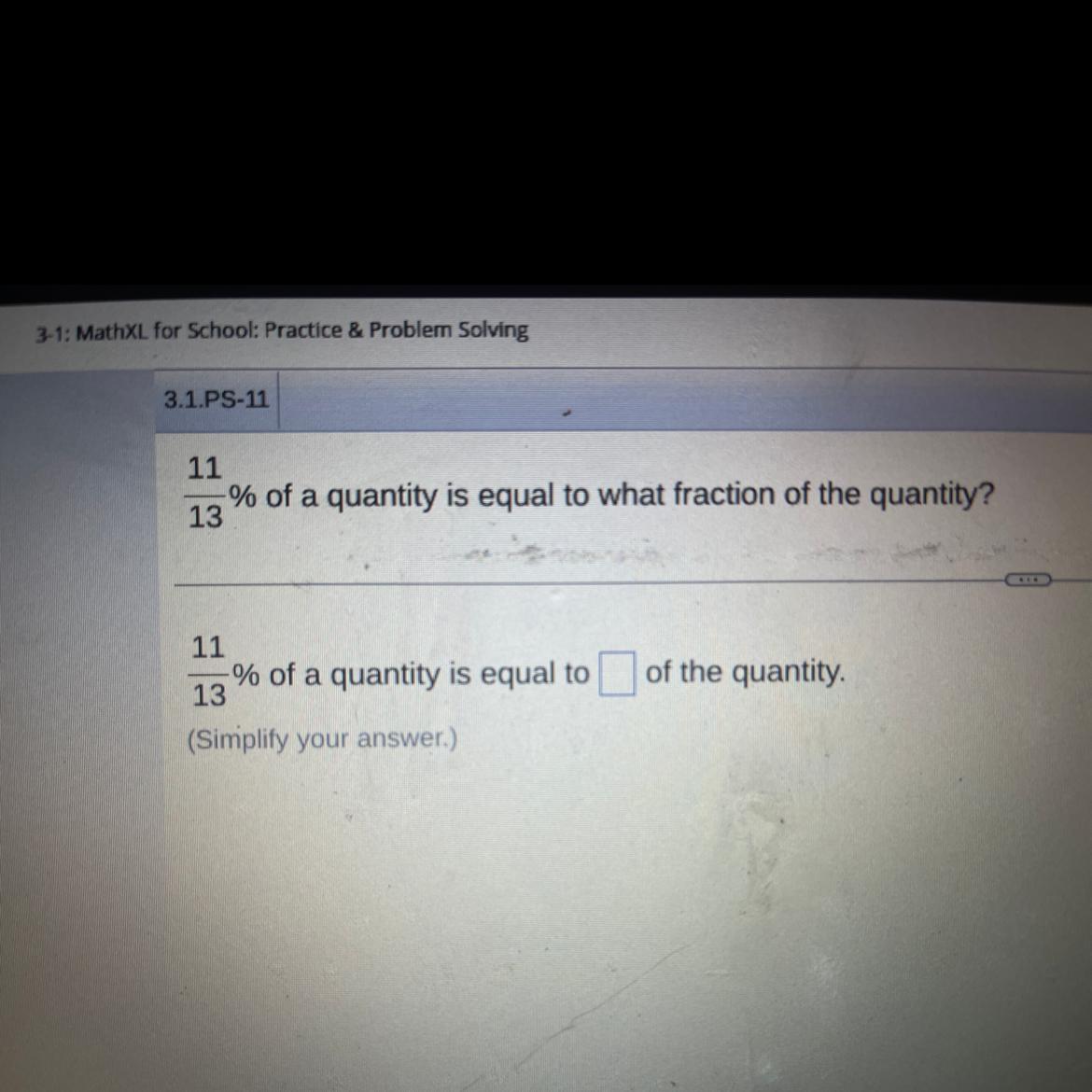
Answers
\(\frac{11}{13}\) % of a quantity is equal to 0.00846 of the quantity.
What do you mean by percentage?A percentage is a figure or ratio that can be stated as a fraction of 100 in mathematics. If we need to determine a percentage of a number, multiply it by 100 and divide it by the total. So, a part per hundred is what the percentage refers to. Percent signifies for every 100. The sign "%" is used to denote it.
When a fraction of a whole is expressed as a number between 0 and 100, it is called a percentage. All of something is 100 percent, half of it is 50 percent, and none of it is 0%.
11/ 13 % of a quantity or 0.846 % of a quantity means
0.846 / 100 = 0.00846
To know more about percentage and quantity you may visit the link which is mentioned below:
https://brainly.com/question/20885539
#SPJ13
You deposit $2000 into a savings account giving 7% interest compounded only at the end of the year. To nearest dollar, what is your end-of-year balance?
Answers
well, you'd have the 2000 plus the 7% :|
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{7\% of 2000}}{\left( \cfrac{7}{100} \right)2000}\implies 140~\hfill \underset{ new~balance }{\stackrel{ 2000~~ + ~~140 }{\text{\LARGE 2140}}}\)
A = P(1 + r/n)^(nt)
Where:
A = the end-of-year balance
P = the principal amount (initial deposit)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded in a year
t = the time (in years)
In this case, P = $2000, r = 7% = 0.07, n = 1 (compounded annually), and t = 1 (one year).
Plugging these values into the formula, we get:
A = 2000(1 + 0.07/1)^(1*1)
A ≈ $2,140.00
Therefore, to the nearest dollar, the end-of-year balance is $2,140.
On average, seawater in the worlds oceans a salinity of about 3.5%. About how much salt is there in 100g of seawater
Answers
Answer:
3.5% means that their is 3.5 grams of salt in 100 grams of water
so 3.5 grams
Hope This Helps!!!
Answer:
3.5 grams
Step-by-step explanation:
Given the following question:
100 grams of sea water
3.5% of salinity
In order to find the answer, we have to find 3.5% of 100.
\(\frac{3.5\times100}{100} =3.5\times100=350\div100=3.5\)
\(=3.5g\)
Hope this helps.
help? its from khan academy

Answers
Answer:
the answer is y=3x+3
Step-by-step explanation:
Answer: 3x+3
Step-by-step explanation:
Find the mx+b
B= 3, starting point on y-axis
M = 3, find rise over run.
What is the area of the real object that the scale drawing models?
Scale factor: 1:8
Area =
2 square cm
Scale drawing
Object
O A. 128 square cm
B. 16 square cm
O C. 256 square cm
OD. 2 square cm
Answers
The area of the real object represented by the scale drawing is 128 square cm. Thus, the correct answer is option A: 128 square cm.
A scale factor of 1:8 means that every measurement on the scale drawing is 1/8th of the corresponding measurement on the real object. Since the scale drawing has an area of 2 square cm, we need to determine the area of the real object.
To find the area of the real object, we can use the relationship between the scale factors of length and area. Since the scale factor is 1:8, the length ratio between the scale drawing and the real object is 1:8. However, the area ratio is squared, so the area ratio between the scale drawing and the real object is (1:8)^2, which simplifies to 1:64.
Since the area of the scale drawing is 2 square cm, we can multiply it by the area ratio (1:64) to find the area of the real object.
2 square cm * 64 = 128 square cm.
Therefore, the area of the real object represented by the scale drawing is 128 square cm. Thus, the correct answer is option A: 128 square cm.
Learn more about area here: https://brainly.com/question/13194650
#SPJ11
Savannah is making pots and plates to sell at a local art fair. Each pot weighs 2 pounds and each plate weighs 1 pound. Savannah cannot carry more than 50 pounds to the fair. She only has enough clay to make 40 plates. In addition, she only has enough clay to make 24 pots. She will make $12 profit on every plate and $25 for every pot that she sells. How many pots and how many plates should Savannah make to maximize her profit?
Answers
Answer:
24 pots 2 plates
Step-by-step explanation:
Answer:
24 pots and 2 plates
Step-by-step explanation:
(45x) = (25x) (57+x)
Answers
Answer:
x = 0; x = \(\frac{-276}{5}\)
Step-by-step explanation:
45x = 25x(57 + x)
45x = 1425x + 25x²
25x² + 1425x - 45x = 0
25x² + 1380x = 0
5x(5x + 276) = 0
\(\left \{ {{5x=0} \atop {5x + 276=0}} \right.\)
\(\left \{ {{x=0} \atop {x=\frac{-276}{5} }} \right.\)
A certain triangle has two 45° angles. What type of triangle is it?
• A. Acute isosceles
• B. Right isosceles
O C. Right scalene
• D. Acute scalene
Answers
The type of triangle is a Right isosceles triangle.
What is a right isosceles triangle?An isosceles triangle is a type of triangle with two angles equal and corresponding sides equal. A right angle triangle is a type of triangle in which one if it's sides is exactly 90°.
Therefore an Isosceles Right Triangle is a right triangle that consists of two equal length legs.
This means one side must be 90° and the other two angles must be equal.
Therefore the value of the other two angles =
2x +90 = 180
2x = 180-90
2x = 90
x = 90/2
x = 45°
therefore each side will be 45°
learn more about Right isosceles triangle from
https://brainly.com/question/22795716
#SPJ1
8 cm
15 cm
20 cm
What is the surface area of the cuboid?

Answers
Answer:
Step-by-step explanation:
remember that the surface area is
S=2lw+2lh+2hw
S=2(15*20)+2(15*8)+2(8*20)=600+240+320=1160 cm^2
The surface area of the cuboid is 1160 square cm whose dimensions are
l= 20cm, w= 8 cm and h = 15 cm.
Given:
Length = 20 cm
width = 8 cm
Height = 15 cm
So, the formula for Surface area of Cuboid is
= 2(lw+ wh + lh)
Substituting the values l= 20cm, w= 8 cm and h = 15 cm into the formula as
= 2(lw+ wh + lh)
= 2 (20 x 15 + 8 x 15 + 8 x 20)
= 2 (300 + 120 + 160)
= 2 (580)
= 1160 square cm
Learn more about Surface area here:
https://brainly.com/question/29298005
#SPJ4
Marge purchased x bicycle helmets and y tire pumps. Each helmet cost $12.00 and each pump cost $8.00. She purchased a total of 18 items and spent $176.00. How many helmets did Marge buy?
Answers
Y=10 pumps
Answer:
8 x 12 = 96 10 x 8 = 80 96 + 80 = 176 so the answer is 8 helmets and 10 pumps
Step-by-step explanation:
Given cos(x) 1 7 with 270º < x < 360°. Find tan(2x). -8V3 47 b) O 873 47 473 47 -4√3 47 473 49 f) O None of these.
Answers
The answer of the given question based on the trigonometry is , the value of tan(2x) is - (16√10) / 9.Option (f) is correct. None of these.
Given: cos(x) = -7/3
Here, we have to find the value of tan(2x) Formula used:
tan(2x) = 2tan(x) / (1 - tan²(x))
Now, we have to find the value of tan(x).
For that, we will use the Pythagorean identity, i.e.,
sin²(x) + cos²(x) =
1cos(x) = -7/3sin²(x) + (-7/3)²
= 1sin²(x) = 1 - (-7/3)²
= 1 - 49/9= (9 - 49) / 9
= -40/9 [We took negative square root because 270° < x < 360°, in which sin(x) is negative]
sin(x) = - √(40/9)
= - (2√10)/3tan(x)
= sin(x) / cos(x)
= - √40 / 7
Now, putting the value of tan(x) in the formula,
tan(2x) = 2tan(x) / (1 - tan²(x))
= 2(-√40/7) / [1 - (-40/49)]
= - (16√10) / 9
So, the value of tan(2x) is - (16√10) / 9.Option (f) is correct. None of these.
To know more about Pythagorean identity visit:
https://brainly.in/question/1157534
#SPJ11
Simplify 7^-6 into fraction form using a positive exponent.
Answers
Answer:
\(\frac{1}{7^6}\)
Step-by-step explanation:
When we have a negative exponent in the form a^-x, this is equal to 1/a^x.
We can apply this here, where a = 7, and x = 6.
Hence, 7^-6 = 1/(7^6)
how many different 9-digit pins are there where exactly three of the digits are the same and none of the remaining digits may be repeated?
Answers
This can be calculated by taking 10 (the number of digits available) to the power of 6 (the number of digits that must be different) and multiplying that by 10 (the number of digits available to be repeating number). 10^6 * 10 = 3,628,800.
The number of different 9-digit pins where exactly three of the digits are the same and none of the remaining digits may be repeated can be calculated using the formula 10^6 * 10. The first part is 10^6, which is taking 10 (the number of digits available) to the power of 6 (the number of digits that must be different). This means that each of the 6 digits that must be different can be any of the 10 digits available. The second part is the multiplication of 10 (the number of digits available). This is to represent the fact that the remaining three digits can be any of the 10 digits available, and none of them can be repeated. Finally, the result of 10^6 * 10 is 3,628,800, which is the number of different 9-digit pins where exactly three of the digits are the same and none of the remaining digits may be repeated.
Learn more about repeating number here
https://brainly.com/question/607253
#SPJ4
There are 20 wild pigs on an island and the number of pigs doubled each year for the past 5 years how would one describe the graph of this model
Answers
...............
Answer:
There are 640 pigs after 5 years.
Step-by-step explanation:
if it doubles each year the first year it doubles it is 40 then the second 80 third 160 fourth 320 and fifth 640.
graph it by having the X axis the years and the Y axis do it by 40s
Can someone please help! And thank you!

Answers
Answer:
x = 20
Step-by-step explanation:
X = 20 Because the values are Corresponding Angles This means that they are congruent
solve for x and show full work

Answers
Answer:
x = 8
Step-by-step explanation:
since the triangles are similar then the ratios of corresponding sides are in proportion , that is
\(\frac{RT}{WU}\) = \(\frac{RS}{WV}\) ( substitute values )
\(\frac{6x+15}{28}\) = \(\frac{108}{48}\) ( cross- multiply )
48(6x + 15) = 28 × 108 = 3024 ( divide both sides by 48 )
6x + 15 = 63 ( subtract 15 from both sides )
6x = 48 ( divide both sides by 6 )
x = 8
The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b). True False
Answers
The statement "The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b)" is False.
In a uniform distribution, the probability density function (PDF) is constant within the interval [a, b]. The height of the PDF represents the density of the probability distribution at any given point within the interval. Since the PDF is constant, the height remains the same throughout the interval.
To determine the height of the PDF, we need to consider the interval length. In a uniform distribution defined on the interval [a, b], the height of the PDF is 1/(b - a) for the PDF to integrate to 1 over the entire interval. This means that the total area under the PDF curve is equal to 1, representing the total probability within the interval [a, b].
Therefore, the correct statement is that the height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is not 1/(a - b), but rather it is a constant value necessary for the PDF to integrate to 1 over the interval, i.e., 1/(b - a).
Learn more about uniform distribution here:
https://brainly.com/question/32291215
#SPJ11
Gary is buying a $1,250 computer on an installment plan. He makes a down payment of $150. He has to make monthly payments of 48.25 for 2 1/2 years. What is the total finance charge?
Answers
Answer:
Step-by-step explanation:
Down payment = $150
Monthly Payment = $48.5
Buyer price = $1250
Number of months = 30 (2 1/2 years)
The total amount of monthly payments = Monthly payments × Number of months
= 48.5 × 30
= 1447.50
The total cost = Total amount of monthly payments + Down payments
= 1447.50 + 150
= 1597.50
Finance charge = Total cost - Buyer price
= 1597.50 - 1250
= 347.50
PLEASE ANSWER I WILL GIVE YOU BRAINIEST!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
C. x > 15
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
how much simple interest is earned on $7500 at a rate of 3% in 5 years?
Answers
The rule of the simple interest is
I = Prt, where
P is the money invested
r is the rate
t is the time
In the question
P = $7500
r = 3% = 3/100 = 0.03
t = 5
Substitute these values in the equation above
\(I=7500\times0.03\times5\)I = 1125
The interest is $1125
Michael just started middle school this year, and his grandmother will give him some money to buy new spirit wear. After he buys a hoodie for $30, Michael figures he'll need at most $15 more to buy a T-shirt.
Let x represent how much money Michael expects to spend on spirt wear. Which inequality describes the problem?
Solve the inequality. Then, complete the sentence to describe the solution.
Michael expects to spend at most $_______
on spirit wear.
Answers
The inequality that describes the problem is x - 30 ≤ 15
Inequality problemLet x represent how much money Michael expects to spend on sports wear
If Michael just started middle school this year, and his grandmother will give him some money to buy new spirit wear and buys hoodie for $30, the balance remaining will be x - 30
If Michael figures he'll need at most $15 more to buy a T-shirt, hence the resulting inequality will be:
x - 30 ≤ 15
Add 30 to both sides
x - 30 + 30 ≤ 15 + 30
x ≤ 45
Hence the inequality that describes the problem is x - 30 ≤ 15 and Michael expects to spend at most $45 on sports wear.
Learn more on inequality here: https://brainly.com/question/24372553
2. How many 3 -digit even numbers can be formed from the digits 1,2,3,4,5,6 if the digits can be repeated?
Answers
Step-by-step explanation:
First digit : 6 choices
Second digit: 6 choices
Third digit: 3 choices ( 2, 4 or 6 to be an even number)
6 x 6 x 3 = 108 possibles
a triangle has vertices (0, 0, 0), (1, 1, 1), and (0, −6, 7). find its area.
Answers
The area of the triangle is 25 square units.
we can use the formula for the magnitude of the cross product of two vectors. Let's consider two vectors formed by the given points: vector A = (1, 1, 1) - (0, 0, 0) = (1, 1, 1) and vector B = (0, -6, 7) - (0, 0, 0) = (0, -6, 7). The cross product of A and B can be calculated as follows:
A × B = |i j k |
|1 1 1 |
|0 -6 7 |
The cross product A × B yields the vector (-13, -7, -6). The magnitude of this vector can be calculated using the formula: √((-13)^2 + (-7)^2 + (-6)^2) = √(169 + 49 + 36) = √254 = 2√(63) ≈ 15.94. Since the area of a triangle is half the magnitude of the cross product of two of its sides, the area of the given triangle is 0.5 * 15.94 = 7.97 square units.
learn more about vectors here:
https://brainly.com/question/24256726
#SPJ11
In the coordinate plane three vertices of rectangle ABCD are A(0,0), B(0,a) and D(b,0). What are the coordinates of point C?

Answers
Answer:
C (a, b) is the cordinates of point c.
In 1927, Charles Lindburgh had his first solo flight across the Antlantic Ocean. He flew 3,610 miles in 33.5 hours. If he flew about the same number of miles each hour, how many miles did he fly each hour?
Answers
Answer:
107.76
Step-by-step explanation:
We are told in the above question that:
He flew 3,610 miles in 33.5 hours. If he flew about the same number of miles each hour, how many miles did he fly each hour?
We solve the above question by:
33.5 hours = 3610 miles
1 hour = x miles
Cross Multiply
33.5 hours × x miles = 3610 miles × 1 hour
x miles = 3610 miles × 1 hour/33.5 hours
x miles = 107.76119403 miles
Approximately = 107.76 miles per hour
Therefore, he flew 107.76 miles each hour
List pairs of congruent angles and the extended proportion that relates the corresponding sides for the similar polygons. Given ABDF ~ VXZT
** I NEED HELP I KEEP GETTING IT WRONG**

Answers
Given:
\(ABDF\sim VXZT\)
To find:
The pairs of congruent angles and the extended proportion that relates the corresponding sides for the similar polygons.
Solution:
We have,
\(ABDF\sim VXZT\)
The corresponding angles of similar polygons are congruent. So,
\(\angle A\cong \angle V\)
\(\angle B\cong \angle X\)
\(\angle D\cong \angle Z\)
\(\angle F\cong \angle T\)
The corresponding sides of similar polygons are proportional. So,
\(\dfrac{AB}{VX}=\dfrac{BD}{XZ}=\dfrac{DF}{ZT}=\dfrac{A F}{VT}\)
Therefore, the required solutions are \(\angle A\cong \angle V,\angle B\cong \angle X,\angle D\cong \angle Z,\angle F\cong \angle T\) and \(\dfrac{AB}{VX}=\dfrac{BD}{XZ}=\dfrac{DF}{ZT}=\dfrac{A F}{VT}\).
solve general solutions
\( \sqrt{3tan \:} (2x - 10) + 1 = 0\)
Answers
\(\\ \rm\Rrightarrow \sqrt{3tan(2x-10)}+1=0\)
\(\\ \rm\Rrightarrow \sqrt{3tan(2x-10)}=-1\)
\(\\ \rm\Rrightarrow 3tan(2x+10)=1\)
\(\\ \rm\Rrightarrow tan(2x+10)=1/3\)
1/3=0.33..tan^{-1}(0.33)≈18\(\\ \rm\Rrightarrow 2x+10=18\)
\(\\ \rm\Rrightarrow 2x=8\)
\(\\ \rm\Rrightarrow x=4\)
Please help me solve this equation please and thank you

Answers
Answer:
0,3
Step-by-step explanation:
6x + 3y = 9
+ -6x + 4y = 12
=
7y = 21
y = 3
Replace 3 into one of the equations and solve for x
6x + 3(3) = 9
6x + 9 = 9
6x = 0
x = 0
MATH GENUISES HELP FAST AND WITH ACCURACY PLS
When two electrical resistors are connected in a parallel circuit, the reciprocal of the total resistance (1/Rn) of the combination is the sum of the reciprocals of each resistance. This relationship is expressed like so: 1/Rn=1/R1+1/R2
R1 is the first resistance and 1/R1 is the RECIPROCAL of the first resistance. Likewise, R2 is the second resistance and 1/R2 is the RECIPROCAL of the second resistance.
If the reciprocal of the resistance of the combination is .2, the resistance of the first resistor (R1) is x + 4, and the resistance of the second resistor (R2) is 5x, find x. State your answer in simplified radical form, if necessary.
Answers
Using the formula for the equivalent resistance that we have known from the question; x = -9 ± √91/5
What is the equivalent resistance?The equivalent resistance is a measure of the total resistance of a circuit that is made up of multiple resistors. When resistors are connected in a circuit, they can be arranged in series or parallel configurations, which affects the overall resistance of the circuit.
Using;
1/Rn = 1/R1 + 1/R2
1/2 = 1/x + 4 + 1/5x
1/2 = 5x + x + 4/5x (x + 4)
1/2 = 6x + 4/5x^2 + 20x
6x + 4 = 10x^2 + 40x
10x^2 - 6x + 40x - 4 = 0
10x^2 + 36x - 4 = 0
x = -9 ± √91/5
Learn more about equivalent resistance:https://brainly.com/question/13606415
#SPJ1