Solve for x to find the value that makes these ratios proportional. x/12 = 5/7
Answers
Answer:
8.57
Step-by-step explanation:
\( \frac{x}{12} = \frac{5}{7} \\ 7x = 60 \\ x = 8.5714\)
Related Questions
A puzzle has 1080 pieces. How many pieces are 80% of the puzzle?
Answers
Answer:
864
Step-by-step explanation:
80/100 simplified is 4/5
so you do 4/5 of 1080
which is 1080 divided by 5 that is 216
and then 216 x 4 which is 864
center (-4, -7), tangent to x = 2
Answers
Answer:
(x + 4)^2 + (y + 7)^2 = 36
Step-by-step explanation:
The given information describes a circle with its center at (-4, -7) and tangent to the vertical line x = 2. To determine the radius of the circle, we need to find the distance between the center and the tangent line.
The distance between a point (x1, y1) and a line Ax + By + C = 0 is given by:
d = |Ax1 + By1 + C| / sqrt(A^2 + B^2)
In this case, the equation of the line is x = 2, which can be written as 1x + 0y - 2 = 0. Therefore, A = 1, B = 0, and C = -2. The center of the circle is (-4, -7), so x1 = -4 and y1 = -7. Substituting these values into the formula, we get:
d = |1*(-4) + 0*(-7) - 2| / sqrt(1^2 + 0^2)
d = |-6| / sqrt(1)
d = 6
Therefore, the radius of the circle is 6 units. The equation of a circle with center (h,k) and radius r is given by:
(x - h)^2 + (y - k)^2 = r^2
Substituting the values we have found, we get:
(x + 4)^2 + (y + 7)^2 = 36
This is the equation of the circle that satisfies the given conditions.
if 15/3 greater than 7, then 15/7 is less than 3 true or false
Answers
Answer:
True
Step-by-step explanation:
15/7 is about 2.14 which is less than 3
can someone help me on number 4

Answers
Answer:
\(P = 48 in\),\(A= 120in^2\)
Step-by-step explanation:
Again we can use Pythagorean theorem to find the missing side
x^2 + 15^2 = 17^2
x^2 + 225 = 289
Subtract 225 from both sides
x^2 = 64
Find the square root of both sides
√x^2 = √64
x = 8
So
l = 15in, w = 8in
P=2(15) + 2(8)
P = 30 + 18
P = 48 in
A= 15(8)
A= 120in^2
Write 3 × 107 km3, the total volume of the continental Antarctica ice sheet, as a basic numeral.
___km^3
Answers
The total volume of the continental Antarctica ice sheet, as a basic numeral. 31,000,000 km³.
What is volume?The space occupied by any solid in a three-dimensional space is called the volume of the solid. For Antarctica, the volume will be the space occupied by the ice present in three-dimensional space.
Let us first gather the information needed Land area of Antarctica = 14,000,000 KM squared
The average thickness of Antarctic ice = 2.15 KM
Earth’s oceans cover a total surface area of 340,000,000 KM²
The ice melts into water, the resulting water volume is about 5/6 of the original ice.
(5/6) x (14,000,000 km) x (2.15 km) = 340,000,000 km
14,000,000km² x 2.15km = 31,000,000 km³
Therefore, the total volume of the continental Antarctica ice sheet is a basic numeral. 31,000,000 km³.
To know more about volume follow
https://brainly.com/question/4275240
#SPJ1
Please help me please help me help please help me

Answers
y-2=-11(x-5)
f(x) = 11x - 2. Find x when f(x) = 64
please show steps
Answers
Answer: the correct value of x in this will be 6.
Step-by-step explanation: According to the equation given ,
f(x) = 64
so , f(x) = 11x - 2 now putting the value of f(x) in this equation
therefore , 64 = 11x - 2
now solving the equation , 11x= 64+2
11x = 66
x = 66/11
x = 6
thus, the value of x obtained from the equation is 6
Tenzin has purchased a minivan for $35 000. The value (V), in dollars, of the
minivan as a function of time (t), in years, depreciates according to the function
V(t) = 35000(0.5)^t/3. How long will it take for Tenzin's minivan to depreciate to 15% of its initial value?
(Equation included below for clarity).
\(v(t) = 35000( \frac{1}{2} )^{ \frac{t}{3} } \)
Answers
Answer:
About 8.2 years.
Step-by-step explanation:
The minivan was purchased for $35,000 and it depreciates according to the function:
\(\displaystyle V(t)=35000\Big(\frac{1}{2}\Big)^{t/3}\)
Where t is the time in years.
And we want to determine how long it will take for the minivan to depreciate to 15% of its initial value.
First, find 15% of the initial value. This will be:
\(0.15(35000)=5250\)
Therefore:
\(\displaystyle 5250=35000\Big(\frac{1}{2}\Big)^{t/3}\)
Solve for t. Divide both sides by 35000:
\(\displaystyle 0.15=\Big(\frac{1}{2}\Big)^{t/3}\)
We can take the natural log of both sides:
\(\displaystyle \ln(0.15)=\ln(0.5^{t/3})\)
Using logarithmic properties:
\(\displaystyle \ln(0.15)=\frac{t}{3}\ln(0.5)\)
Therefore:
\(\displaystyle t=\frac{3\ln(0.15)}{\ln(0.5)}=8.2108...\)
So, it will take about 8.2 years for Tenzin's minivan to depreciate to 15% of its initival value.
For each of the following find:
I. lim f (x) as x approaches a from the negative
II. lim f (x) as x approaches a from the positive
III. lim f (x) as x approaches a
a. f(x)={ sin x/3, if x< or equal to pi a=pi
{ x(root3)/(2pi), if x>pi
b. f(x)= (x^2-36)/root(x^2-12x+36) a=6
Answers
Answer:
a. For the function:
f(x) = { sin x/3, if x ≤ π
{ x√3/2π, if x > π
I. To find lim f(x) as x approaches π from the negative side, we need to evaluate f(x) for values of x that are slightly less than π. In this case, since sin(x/3) is a continuous function, we can simply evaluate it at x = π:
lim f(x) as x approaches π- = f(π-) = sin(π/3) = √3/2
II. To find lim f(x) as x approaches π from the positive side, we need to evaluate f(x) for values of x that are slightly greater than π. In this case, we can simply evaluate the other part of the piecewise function at x = π:
lim f(x) as x approaches π+ = f(π+) = π√3/2π = √3/2
III. To find lim f(x) as x approaches π, we need to check whether the left-hand and right-hand limits are equal. In this case, since both the left- and right-hand limits exist and are equal, we have:
lim f(x) as x approaches π = √3/2
b. For the function:
f(x) = (x^2 - 36)/√(x^2 - 12x + 36)
I. To find lim f(x) as x approaches 6 from the negative side, we need to evaluate f(x) for values of x that are slightly less than 6. In this case, we can substitute x = 6 - h, where h is a positive number approaching zero, to get:
lim f(x) as x approaches 6- = lim f(6 - h) as h approaches 0
Substituting x = 6 - h into the function, we get:
f(6 - h) = [(6 - h)^2 - 36]/√[(6 - h)^2 - 12(6 - h) + 36]
= [h^2 - 12h]/√[h^2]
Simplifying the numerator and denominator separately, we get:
f(6 - h) = h(h - 12)/|h|
Since h approaches 0 from the positive side, we have:
lim f(6 - h) as h approaches 0+ = lim h(h - 12)/h as h approaches 0+ = lim (h - 12) as h approaches 0+ = -12
II. To find lim f(x) as x approaches 6 from the positive side, we need to evaluate f(x) for values of x that are slightly greater than 6. In this case, we can substitute x = 6 + h, where h is a positive number approaching zero, to get:
lim f(x) as x approaches 6+ = lim f(6 + h) as h approaches 0
Substituting x = 6 + h into the function, we get:
f(6 + h) = [(6 + h)^2 - 36]/√[(6 + h)^2 - 12(6 + h) + 36]
= [h^2 + 12h]/√[h^2]
Simplifying the numerator and denominator separately, we get:
f(6 + h) = h(h + 12)/|h|
Since h approaches 0 from the positive side, we have:
lim f(6 + h) as h approaches 0+ = lim h(h +
Step-by-step explanation:
Please help me quickly I only have till 11:59 please

Answers
SOLUTION:
Case: Rate
Method:
2/3 of the wind distance is:
\(\begin{gathered} \frac{2}{3}\times2400 \\ =1600m \end{gathered}\)Since the direction is against the wind, the speed with during the wind is:
\(\frac{1600\text{ }m}{10\text{ }mins}=16\text{ }m\text{ }per\text{ }min\)Speed without the wind
\(\frac{2400m}{10mins}=24m\text{ }per\text{ }min\)The rate of the wind is:
24 - 16 = 8 m per min
Final answer:
8 meters per minute
A car was bought in 2009 for $120000. it 2016 it value decrease by 20%. it's value decrease by 10% of it's value in 2010.fond the value of the car at the end of 2011.
guys I am giving you 100 points do answer me with solution.
and I will mark you as brainlest. BYE!BYE!
Answers
Answer:
This is the case % decrease120000*80/100*90/100=12*80*90=7200*12=72000+ 14400=86400 rsStep-by-step explanation:
is y= 1/2x - 4 equal to 3x - 6y = 24

Answers
Answer:
\(\fbox{\begin{minipage}{4em}Yes, it is\end{minipage}}\)
Step-by-step explanation:
3x - 6y = 24
Divide both sides by 6:
(3/6)x - (6/6)y = 24/6
Simplify:
(1/2)x - y = 4
Move y to the right side, 4 to the left side, and change sign of y and 4:
(1/2)x - 4 = y
Rearrange both sides:
y= (1/2)x - 4
Hope this helps!
:)
The mug is 5/8 full, the mug contains 3/4 of water find the capacity of the mug
Answers
The capacity of the mug is 1.2. The capacity of the mug can be found by using the equation C = (3/4) ÷ (5/8).
What is capacity?It is the maximum amount of output that can be produced in a given period of time. Capacity is usually expressed in terms of units per unit of time, such as gallons per minute or passengers per hour.
In this equation, 3/4 represents the amount of water in the mug, and 5/8 represents the amount the mug is full.
Let the capacity of the mug be x.
Given,
Mug is 5/8 full and contains 3/4 of water
So, 5/8 of the mug is filled with water
Therefore,
5/8 of x = 3/4
(5/8 )x = (3/4)
x = (3/4) × (8/5)
x = (24/20)
x = 1.2
Therefore, the capacity of the mug is 1.2.
For more questions related to gallons
https://brainly.com/question/26007201
#SPJ1
For his birthday , Aaron received four stamps for his collection . his collection already contained eight times that number of stamps. Before pasting the stamps into albums , Aaron divide them equally into three envelope. Which numerical expression models the number of stamps in each envelope? A 12÷3 B 4+32÷3 C (4+32)÷3 D 12×4÷4
Answers
Answer:
C
Step-by-step explanation:
Aaron received four stamps. He already had eight times as much. 32 + 4. Before pasting the stamps into albums, Aaron divides them equally into three envelopes. (32 + 4) ÷ 3.
Find the 19th term in the geometric sequence, the first term being a=4 and the common ratio being r=2
Answers
The 19th term of a geometric sequence is 1048576.
What is a geometric sequence?A geometric sequence is a sequence of numbers in which the ratio between consecutive terms is constant.
We have,
a = 4 and r = 2
The nth term of a geometric sequence.
= a\(r^{n-1}\)
Now,
The 19th term of a geometric sequence.
= a\(r^{n-1}\)
Substituting a and r values.
= 4 x \(2^{19 - 1}\)
= 4 x \(2^{18}\)
= 4 x 262144
= 1048576
Thus,
The 19th term of a geometric sequence is 1048576.
Learn more about geometric sequence here:
https://brainly.com/question/2321576
#SPJ9
2
\(2x - 8x = \)
Answers
Answer:
-6x
Step-by-step explanation:
2x - 8x = -6x
Step-by-step explanation:
Question: 2x – 8x
Do, 2 – 8 which is -6
Then just put the x’s next to them
Answer : 2x – 8x = -6x
Find the mean of the following
data set.
14,24,35,37,43,35,45,24,29,41,45,
Answers
In the past few years, many small businesses have been faced with difficulty keeping their doors open, and in many cases large corporations with cash on hand have come in to take over the companies and their real estate. In such case, a large restaurant chain purchased a small corner tavern with plans to use the name to build a local franchise. The cost of buying the franchise naming rights was four times the cost of buying the physical property. If the total purchase price was $1,250,000, how much did the restaurant chain pay for each individual element of the sale ( naming rights and physical property)?
Answers
The restaurant chain paid $625,000 for the physical property and $2,500,000 for the franchise naming rights, for a total purchase price of $1,250,000.
What is sale?Sale refers to the transfer of ownership of goods or services from one person to another in exchange for money or other consideration.
The total purchase price of the franchise naming rights and physical property was $1,250,000.
To calculate the amount paid for each individual element of the sale, the total purchase price must be divided by the two elements.
The total purchase price of $1,250,000 divided by two elements equals $625,000.
This means that the restaurant chain paid $625,000 for the franchise naming rights and $625,000 for the physical property.
The amount of money paid for the franchise naming rights (four times the cost of buying the physical property) can be calculated by multiplying the cost of the physical property, which is
$625,000/4 .
When the cost of the physical property is multiplied by four, the result is $2,500,000.
This means that the restaurant chain paid $2,500,000 for the franchise naming rights.
In summary, the restaurant chain paid $625,000 for the physical property and $2,500,000 for the franchise naming rights, for a total purchase price of $1,250,000.
For more questions related to purchase price
https://brainly.com/question/31225339
#SPJ1
What is 956.3 written in scientific notation?
Answers
9.563 * 10^2
The decimal number that is multiplied by 10 must be less than a two-digit number.
We move the decimal point to the left for this problem and stop where the decimal is less than a two-digit number.
So, 956.3 becomes 9.56 after moving two places to the left. Moving to the left makes the exponent of 10 positive. Moving to the right, makes the exponent of 10 negative.
We want our answer in the form
(decimal number) x 10^(n).
Answer: 9.56 x 10^2
Understand???
WHAT ANGEL IS ADJACENT!!! HELP ME PLSSSPLSPSL I UPLOADED THE PIC THERE

Answers
Answer:
angle 10
FYI:
angle 10 or 12 is adjacent to 9
(they share an adjacent arm)
angle 11 is opposite adjacent to angle 9.
Help !!
centimeters and millimeters <3

Answers
1 cm = 10 mm. Length of book : 28 cm. Length of book = 280 mm. This shows that measurements in mm are the same but look to have a higher number .
How to compare centimeters and millimeters ?The conversion factor provided states that 1 cm is equal to 10 mm, which means that 1 cm is made up of 10 individual millimeters.
The length of my book in when measured in millimeters is 280 mm.
In centimeters, this is therefore:
= 280 mm / 10 cm /mm
= 28 cm
Although the numerical value appears higher when expressed in millimeters, it is important to note that the actual length of the book remains the same.
Find out more on centimeters at https://brainly.com/question/22462126
#SPJ1
organizations interested in making sure that accused persons have a trial of their peers often compare the distribution of jurors by age, education, and other socioeconomic variables. one such study in a large southern county provided the following information on the ages of 1,000 jurors and the age distribution countywide. Soc. Age 21-40 41-50 51-60 Over 60 Total 399 212 Number of jurors Age % countywide 231 158 1,000 42.1 22.9 15.7 19.3 100 a. Display the above data using appropriate graphs. b. Is this significant evidence of a difference between the age distribution of jurors and the countywide age distribution? c. Does there appear to be an age bias in the selection of jurors?
Answers
Yes, it is significant evidence of a difference between the age distribution of jurors and the countrywide age distribution.
No, there is no age bias in the selection of jurors.
P Oi Ei ( Oi-Ei) ^2/Ei
0.421 399 421 1.149643705
0.229 231 229 0.017467249
0.157 158 157 0.006369427
0.193 193 193 1.870466321
1 1000 1000 3.043946702
The above can be represented in graphs.
Now,
Ei = n × pi
TS = 3.04394672
From TS < value
Value (7.81472)
We fail to reject the null hypothesis at 5% value of significance
No, there is no age bias in the selection of jurors.
To know more about Distribution, refer to:
http://brainly.com/question/4679134
#SPJ4
I need help with this problem

Answers
The area of the region enclosed by the curves can be found to be 1/6 square units.
How to find the area of the region ?To find the area enclosed by the curves y = x, y = 5x, and y = -x + 2, we first need to find the points where these curves intersect.
Intersection points of y = x and y = 5x: (0, 0)
Intersection points of y = x and y = -x + 2: Intersection point: (1, 1)
Intersection points of y = 5x and y = -x + 2: Intersection point: (1/3, 5/3)
Now we have the three intersection points: (0, 0), (1, 1), and (1/3, 5/3). The area enclosed by the curves is a triangle with vertices at these points.
To find the area of the triangle, we can use the Shoelace Formula:
Area = (1/2)|x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|
Area = (1/2)|0(1 - 5/3) + 1(5/3 - 0) + (1/3)(0 - 1)|
Area = 1 / 6 square units
The area enclosed by the curves is 1/6 square units.
Find out more on area at https://brainly.com/question/9485980
#SPJ1
is 1\3x3=1 associative property
Answers
Answer:
No.
Step-by-step explanation:
Associative property, for example, is the process of grouping numbers to find the sum. With this law, you also can multiply/add these numbers together and it will not affect your final answer. In this case, that's not the case. So, the statement is false.
What are the zeroes of the function?
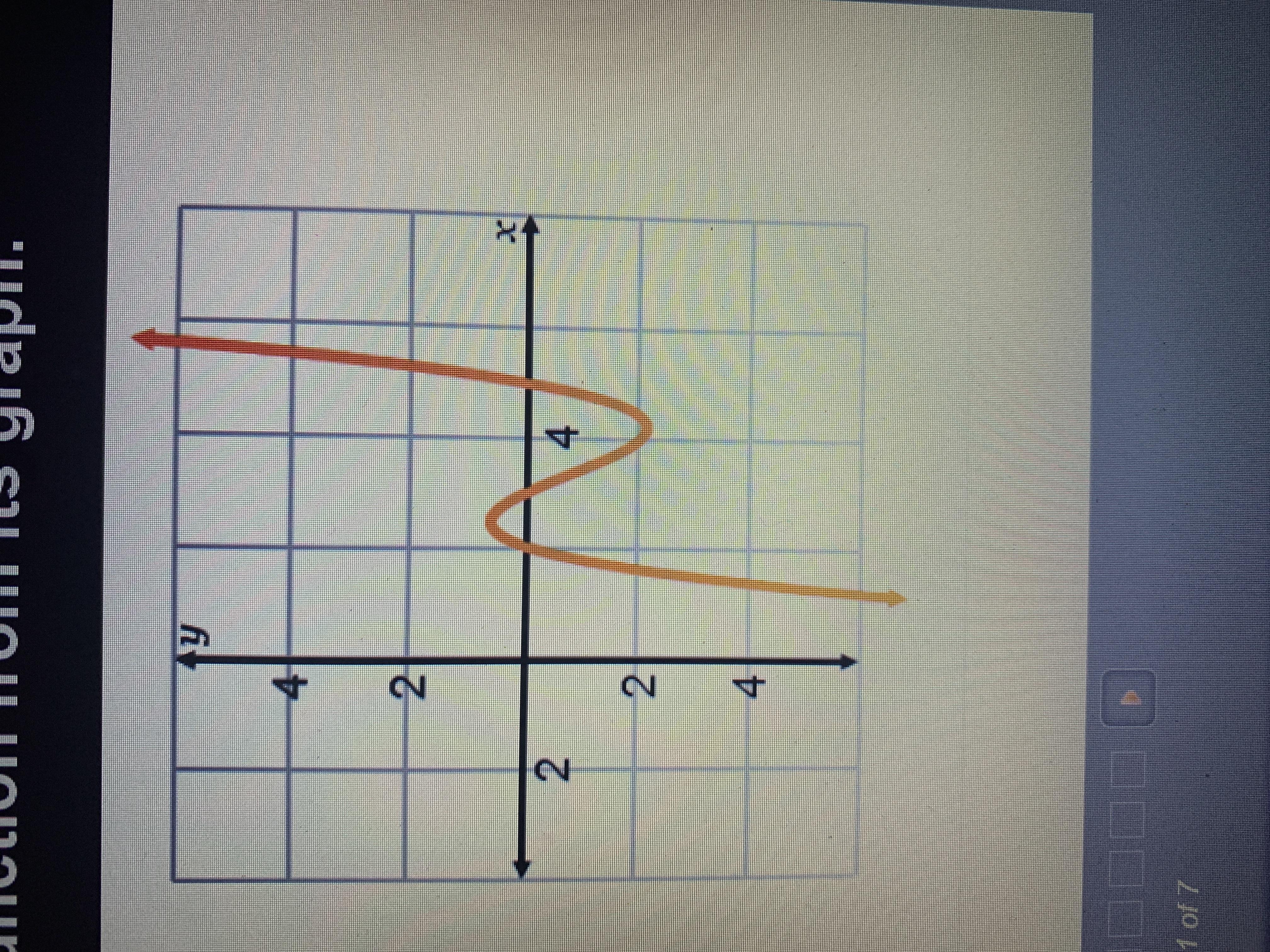

Answers
Answer:
2, 3 and 5
Step-by-step explanation:
Answer:
2,3,5
Step-by-step explanation:
Sam is framing a closet under a stairway. The stairway is 20 ft 6 in. long, and its angle of elevation is 31º. Find the depth of the closet to the nearest inch.
Answers
Answer:
The depth is 127 inches.
Step-by-step explanation:
The stairway and its depth can be compared to a right angled triangle. Let the depth be represented by d.
But,
12 inches = 1 foot
20 ft 6 in = 20 + \((\frac{6}{12} )\)
= 20.5 feet
So that applying the appropriate trigonometric function, we have;
Sin θ = \(\frac{opposite}{hypotenuse}\)
Sin 31º = \(\frac{d}{20.5}\)
d = 20.5 x Sin 31º
= 20.5 x 0.5150
d = 10.5575
d ≅ 11 feet
Therefore,
d = 10.5575 feet = (10.5575 x 12) inches
= 126.69 inches
The depth is 127 inches.
what is the volume of the right cone shown below?

Answers
Answer:
A it's a because 45 x 10³ is 75
Solve for x
x^2 - 8x = -3
Answers
The solutions for the quadratic equation:
x^2 - 8x = -3
Are:
x = 7.6x = 0.4How to solve the quadratic equation?Here we want to solve the quadratic equation:
x^2 - 8x = -3
First we can move all the terms to the left side so we get:
x^2 - 8x + 3 = 0
Using the quadratic formula (or Bhaskara's formula) we can get the solutions for x as:
\(x = \frac{8 \pm \sqrt{(-8)^2 - 4*¨1*3} }{2*1} \\\\x = \frac{8 \pm 7.2 }{2}\)
Then the two solutions for the quadratic equation are:
x = (8 + 7.2)/2 = 7.6
x = (8 - 7.2)/2 =0.4
Learn more about quadratic equations by reading:
https://brainly.com/question/1214333
#SPJ1
(c) use the answers to parts (a) and (b) to estimate by how much the average monthly cell phone bill changed between 1990 and 2008. (round your answer to two decimal places.)
Answers
The area above x axis is 12.6 sq units while the area under the y-axis is 42.443 sq units. The change in the average phone bill is 29.843 units.
a) Here we see that the graph is in the shape of a right-angled triangle above the x-axis
The area of a triangle = 1/2 X Base X Height
Here the base will be the measure of the distance of co-ordinates on the x-axis
The height is the distance between the coordinates on the axis for that triangle
= 1/2 X (16 - 8) X (3.15 - 0)
= 1/2 X 8 X 3.15
= 12.60 sq units
b)
Below the x-axis, the graph is a rectangle and a triangle
The area of the rectangle = length X width
Here length is the distance of the co-ordinates of the y-axis and width is the distance between the coordinates for the x-axis
Hence we get
(0 - (-5.14))(8 - 0)
= 5.14 X 8
= 41.12 sq units for the rectangle.
The area of the triangle will be
1/2 X (18 - 15.48) X (0 - (-1.05))
1/2 X 2.52 X 1.05
= 1.323 sq unit
Hence, the total area is
41.12 + 1.323
= 42.443 sq unit
c)
Since the area under the graph represents change,
Here we see that the change in the average cell phone bill will be
42.443 + 12.6
= 55.043
To learn more about Co-ordinate Geometry visit
https://brainly.com/question/14515991
#SPJ4
Complete Question
(Image Attached)

Find the numbers with the following property three times the sum of four and a number is less than seven times the same number
Answers
Let's represent the number with the variable "x". According to the given property, we can write the following equation:
3(x + 4) < 7x
Now, let's solve this inequality to find the range of numbers that satisfy the property.
3x + 12 < 7x
Subtract 3x from both sides:
12 < 4x
Divide both sides by 4 (since the coefficient of x is 4):
3 < x
So, the range of numbers that satisfy the given property is x > 3.
Therefore, any number greater than 3 will satisfy the condition. For example, 4, 5, 6, 7, 8, etc.Step-by-step explanation:
According to the problem, we know that:
3(4 + x) < 7x
Simplifying:
12 + 3x < 7x
Subtracting 3x from both sides:
12 < 4x
Dividing both sides by 4:
3 < x
So the number we're looking for must be greater than 3.