Solve for x algebraically: 7x-3(4x-8)<6x+12-9x
Answers
Answer:
\(x > 6\)
Step-by-step explanation:
\(7x-3(4x-8) < 6x+12-9x\)
Step 1: Distribute -4 into 4x and -8
\(7x-12x+24 < 6x+12-9x\)
Step 2: Combine like terms on both sides
\(-5x+24 < -3x+12\)
Step 3: Subtract 24 from both sides
\(-5x < -3x-12\)
Step 4: Add 3x to both sides
\(-2x < -12\)
Step 5: Divide both sides by -2 (flip inequality sign)
\(x > 6\)
Hope this answer helped!
Related Questions
Mrs. Cazares went shopping for candy for her students. She bought 6 bags of candy. She had a coupon for $6 off her purchase. If she spent a total of $36, how much was each bag of candy?
Answers
Answer:
7
Step-by-step explanation:
hope you have a great day!
Answer:
6x6=36 so 36+$6 discount, 42
Step-by-step explanation:
42
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
322 divide by 14 explained
Answers
Answer:
23
Step-by-step explanation:
A six-sided die is rolled at the same time as a coin is flipped
a. Are the events independent or dependent?
b. What is the probability of rolling a 4, 5, or 6 AND getting “tails" ?

Answers
Answer:
A. Independent
B. 50%
Step-by-step explanation:
I have 0 idea what this even means? Does anyone know the answer and if you could possibly elaborate if you do? Very confused over here
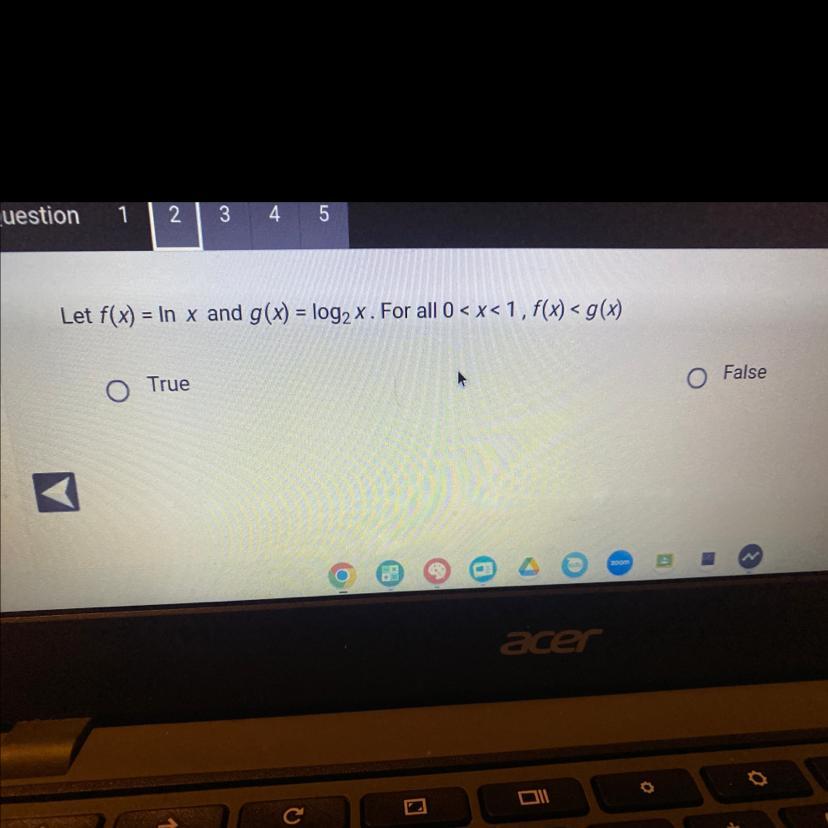
Answers
Let f(x) = lnx and g(x) = log₂x. for all 0 < x < 1, f(x) < g(x): True.
How to determine the corresponding output value for this function?In this scenario and exercise, we would determine the corresponding output value for the functions f(x) and g(x) under the given mathematical operation and independent variables.
When x = 1, the output value for f(x) based on the table of values is given by;
f(x) = lnx
f(1) = ln(1).
f(1) = 0.
When x = 2, the output value for f(x) based on the table of values is given by;
f(x) = lnx
f(2) = ln(2).
f(2) = 0.69314718
When x = 1, the output value for g(x) based on the table of values is given by;
g(x) = log₂x
g(1) = log₂(1)
g(1) = 0.
When x = 2, the output value for g(x) based on the table of values is given by;
g(x) = log₂x
g(2) = log₂(2)
g(2) = 1.
In this context, we can logically deduce that the function f(x) is less than function g(x) for all 0 < x < 1.
Read more on function here: brainly.com/question/10687170
#SPJ1
The average amount of bacteria on the bathroom countertop is 452 bacteria per square inch. How many bacteria would you expect to find on a rectangular bathroom counter top that 1.5ft by 2ft. Round the answer to the highest place value
Answers
First, we need to convert units. In this case, we can convert feets into inches. Since we know that 1 ft=12 in, then we have
\(1.5ft=1.5ft(\frac{12in}{1ft})\)which is equal to
\(\begin{gathered} 1.5ft=(1.5)(12)IN \\ 1.5ft=18IN \end{gathered}\)Similarly, for 2 ft we get
\(\begin{gathered} 2ft=(2ft)(\frac{12In}{1ft}) \\ 2ft=(2)(12In) \\ 2ft=24In \end{gathered}\)Now, we can compare the bacterias in both scenarios. By applying the rule of three, we have
\(\begin{gathered} 452bacteria-----1in^2 \\ x---------(18)(24)in^2 \end{gathered}\)then, x is equal to
\(\begin{gathered} x=\frac{(18)(24)(452)}{1} \\ x=(18)(24)(452) \\ x=195264\text{ bacteria} \end{gathered}\)that is, in an area of (18)(24)in^2 , there are 195,264 bacterias. By rounding to the highest place value, the answer is 200,000 bacterias.
How to do this problem

Answers
Answer:
a. geometric series
b. r_n = 100 × (0.75)^n ft
c. 400
Step-by-step explanation:
a.
Start: 100 ft
After 1 hour: 75% of 100ft = 100 ft × 0.75
After 2 hours: 75% of 100ft × 0.75 = 100 ft × 0.75²
After 3 hours: 75% of 100 ft × 0.75² = 100 ft × 0.75³
Notice what is happening to the radius as the hours pass.
With each passing hour, the radius is 0.75 times the previous radius.
Since each new term is the previous term multiplied by a constant, 0.75, this is a geometric series.
b.
At each hour, multiply 100 ft by 0.75 raised to the number of the hour.
a_n = 100 × (0.75)^n ft
The nth term is 100 times 0.75 to the nth power.
c.
The sum of all the radii is the sum of a series that has 100 as its first term, and each subsequent term is 0.75 times the previous term.
r_n = 100(0.75)^n
Since the constant ratio has an absolute value less than 1, the series has a sum.
S = a_1/(1 - r)
S = sum of infinite series
a_1 = first term
r = constant ratio
S = 100/(1 - 0.75)
S = 100/0.25
S = 400
What is 4 Over 6 divided by 3 Over 12
what The quotient is
Answers
Answer:
2.6
Step-by-step explanation:
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
Sonja's house is 4 blocks west and 1 block south of the center of town. Her school is 3 blocks east and 2 blocks north of the center of town.
Which graph represents this scenario?
(Hint: The center of town should be the origin, and north is up.)
Answers
The answer is \(\sqrt{58} = 7.62\)
So, if you draw this down, you will see that the direct distance is hypotenuse c of a right triangle which sides are 3 blocks (1 south and 2 north) and 7 blocks (4 west and 3 east).
Use the Pythagorean theorem:
\(c^2 = a^2 + b^2\)
\(a = 3\)
\(b = 7\)
\(c^2 = 3^2 + 7^2\)
\(c^2 = 9 + 49\)
\(c^2 = 58\)
\(c = \sqrt{58}\)
\(c = 7.62\)
Can someone help me find the equivalent expressions to the picture below? I’m having trouble

Answers
Answer:
Options (1), (2), (3) and (7)
Step-by-step explanation:
Given expression is \(\frac{\sqrt[3]{8^{\frac{1}{3}}\times 3} }{3\times2^{\frac{1}{9}}}\).
Now we will solve this expression with the help of law of exponents.
\(\frac{\sqrt[3]{8^{\frac{1}{3}}\times 3} }{3\times2^{\frac{1}{9}}}=\frac{\sqrt[3]{(2^3)^{\frac{1}{3}}\times 3} }{3\times2^{\frac{1}{9}}}\)
\(=\frac{\sqrt[3]{2\times 3} }{3\times2^{\frac{1}{9}}}\)
\(=\frac{2^{\frac{1}{3}}\times 3^{\frac{1}{3}}}{3\times 2^{\frac{1}{9}}}\)
\(=2^{\frac{1}{3}}\times 3^{\frac{1}{3}}\times 2^{-\frac{1}{9}}\times 3^{-1}\)
\(=2^{\frac{1}{3}-\frac{1}{9}}\times 3^{\frac{1}{3}-1}\)
\(=2^{\frac{3-1}{9}}\times 3^{\frac{1-3}{3}}\)
\(=2^{\frac{2}{9}}\times 3^{-\frac{2}{3} }\) [Option 2]
\(2^{\frac{2}{9}}\times 3^{-\frac{2}{3} }=(\sqrt[9]{2})^2\times (\sqrt[3]{\frac{1}{3} } )^2\) [Option 1]
\(2^{\frac{2}{9}}\times 3^{-\frac{2}{3} }=(\sqrt[9]{2})^2\times (\sqrt[3]{\frac{1}{3} } )^2\)
\(=(2^2)^{\frac{1}{9}}\times (3^2)^{-\frac{1}{3} }\)
\(=\sqrt[9]{4}\times \sqrt[3]{\frac{1}{9} }\) [Option 3]
\(2^{\frac{2}{9}}\times 3^{-\frac{2}{3} }=(2^2)^{\frac{1}{9}}\times (3^{-2})^{\frac{1}{3} }\)
\(=\sqrt[9]{2^2}\times \sqrt[3]{3^{-2}}\) [Option 7]
Therefore, Options (1), (2), (3) and (7) are the correct options.
If a ball is thrown in the air with an initial
height of 4 feet, and if the ball remains in
the air for 3.8 seconds, then accurate to
the nearest foot, how high did it go?
Remember, the acceleration due to
gravity on Earth is -32 ft/sec².
[?] feet
Answers
The requried ball reached a maximum height of approximately 62 feet
Let the ball is thrown vertically upward, we can use the following formula to find the maximum height it reaches:
\(h(t) = -16t^2 + vt + h_0\)
here, h(t) is the height of the ball at time t, v is the initial velocity of the ball (in feet per second), and h0 is the initial height of the ball (in feet). We can also use the fact that the ball remains in the air for 3.8 seconds, which means that the time it takes to reach the maximum height is half of that or 1.9 seconds.
At the highest point, the ball's velocity is zero, so we can find the initial velocity by setting v = 0 in the above formula and solving for h₀:
h₀ = h(t) + 16t²
= 4 + 16(1.9)²
≈ 4 + 57.76
≈ 61.76
Therefore, the ball reached a maximum height of approximately 62 feet
Learn more about the law of motion here:
https://brainly.com/question/29775827
#SPJ1
Plz i NEED HELP ABOUT TO FINISH THIS CLASS! PLZ
17. Does the following system have a unique solution? Why?

Answers
Answer:
last one
Step-by-step explanation:
What percentage of growth is needed annually to reach 400,000 in 3 years if today I have 200,000
Answers
Answer:
approx 26%
Step-by-step explanation:
you try find the multiplier
200000 * 1. ???? ^3= 400000
rearrange equation
\(\sqrt[3]{\frac{400000}{200000} }\) = multiplier
1.25992105
subract one
0.25992105
multiply by 100 to get percentage
25.9%
rounded to whole number = 26%
the difference of x and 22 is equal to 8
Answers
Answer:
Step-by-step explanation:
x - 22 = 8
Lets find variable x.
To isolate the variable, we need to add 22 to both sides.
x = 30
22-14=8
Hope that helped :)
Somebody else has to comment for me to Mark u as BRAINLIEST!! It won't let me

Answers
Answer:
7.5 is the difference
Step-by-step explanation:
basketball mean
(13+22+23+24+36+37+42+43+58+69) ÷10 = 36.7
tennis mean
(14+23+24+38+47+48+57+58+66+67) ÷10 = 44.2
tennis mean - basketball mean
44.2 - 36.7= 7.5
a total of 442 tickets were sold for the school play. They were either adult tickets or student tickets. There were 58 fewer
Answers
Complete Question:
A total of 442 tickets were sold for the school play. They were either adult tickets or student tickets. There were 58 fewer
There were 58 fewer student tickets sold than adult tickets. How many adult tickets were sold?
Answer:
250 adults tickets
Step-by-step explanation:
Given
Represent Adult with A and Children with C
\(Total = 442\)
\(A = C + 58\)
Required
Find A
Since the ticket were either bought by A or C; then
\(A + C = Total\)
This gives:
\(A + C = 442\)
Substitute C + 58 for A
\(C + 58 + C = 442\)
Collect Like Terms
\(C + C = 442 - 58\)
\(2C = 384\)
Divide through by 2
\(C = 192\)
Recall that:
\(A = C + 58\)
\(A = 192 + 58\)
\(A = 250\)
Hence, 250 adults bought the ticket
Rodea la operación equivalente 1/4+2/8=
Answers
Respuesta: 1/4+2/8 = 2/8+2/8
Explicación paso a paso: 1/4 es equivalente a 2/8
Round 84,502 to the nearest thousand
Answers
Use the diagram to the right to complete the statement.
If m2KLJ = 138° then m LMDF=

Answers
Answer: 138
Step-by-step explanation:
\(\angle KLJ \cong \angle MDF\) by the corresponding angles theorem.
x-int:
Y-int
Domain
Range
Absolute max
Relative max
Absolute min
Relative min
Int inc
Int Dec
Positive interval
Negative interval
Symmetry odd,even,neither
Left end behavior
Right end behavior
PLSSS HELPP
Answers
These terms are related to the properties and characteristics of a function, which is a mathematical rule that relates each input value to a unique output value.
What are the properties of function?
Here is a brief explanation of each term:
X-intercept: The x-intercept of a function is the point where the graph of the function crosses the x-axis. It is the value of x for which the value of y is zero.Y-intercept: The y-intercept of a function is the point where the graph of the function crosses the y-axis. It is the value of y for which the value of x is zero.Domain: The domain of a function is the set of all possible input values (x-values) for which the function is defined. It is the set of all values of x that make the function meaningful.Range: The range of a function is the set of all possible output values (y-values) that the function can produce. It is the set of all values of y that can be obtained by applying the function to its domain.Absolute maximum: The absolute maximum of a function is the highest point on the graph of the function, regardless of whether it is a local or global maximum.Relative maximum: The relative maximum of a function is the highest point on the graph of the function in a given interval or neighborhood.Absolute minimum: The absolute minimum of a function is the lowest point on the graph of the function, regardless of whether it is a local or global minimum.Relative minimum: The relative minimum of a function is the lowest point on the graph of the function in a given interval or neighborhood.Increasing interval: An increasing interval of a function is an interval where the function is increasing, i.e., the y-values are getting larger as the x-values increase.Decreasing interval: A decreasing interval of a function is an interval where the function is decreasing, i.e., the y-values are getting smaller as the x-values increase.Positive interval: A positive interval of a function is an interval where the y-values are positive.Negative interval: A negative interval of a function is an interval where the y-values are negative.Symmetry (odd, even, neither): A function is said to be odd if it satisfies the condition f(-x) = -f(x) for all x in the domain. A function is said to be even if it satisfies the condition f(-x) = f(x) for all x in the domain. A function is said to be neither odd nor even if it does not satisfy either of these conditions.Left-end behavior: The left-end behavior of a function is the behavior of the function as x approaches negative infinity.Right-end behavior: The right-end behavior of a function is the behavior of the function as x approaches positive infinity.To know more about function, visit:
https://brainly.com/question/30721594
#SPJ1
Solve using the quadratic formula: -6x2 - 4x + 2 = 0.
Answers
Answer:
6x2+4x-2=0(changing the sign )
Step-by-step explanation:
x=-4+-\(\sqrt\)16+48/12
=-4+-8/12
-4+8/12,-4-8/12
1/3.-1
I not understand this any help please answer and explain please

Answers
The length the line segment DF is 21 units
What is Similarity of Triangles?
Two objects are comparable in Euclidean geometry if they have the same form or one has the same shape as the mirror image of the other. More exactly, one can be created by evenly scaling the other, potentially with extra translation, rotation, and reflection.
Since, the question is incomplete I can only assume that the traingles are similar
So, by rule of similarity we can say that ED/BA = DF/AC
by this 15/5 = DF/7
This implies that the length of DF is 21 units
To learn more about Similarity of Triangle from the given link
https://brainly.com/question/1058720
#SPJ1
Find the mode, median, mean, and range for each data set. Round the mean to two decimals places, where necessary.

Answers
Answer:
The median, mean, and mode of the data set are 5, 4.8, and both 4 and 5 respectively.
Step-by-step explanation:
To find the median of a data set, line up all values from greatest to least and find the number in the center. For example, in the set 1; 2; and 3, 2 would be the median. In this case, the order would be 2, 4, 4, 4, 5, 5, 5, 6, 6, 7. The two numbers in the middle are 5 and 5, their average is 5, so that would be the median. The mean of a data set is the average of all data values in a set. In this case, there are 10 data values, and their total sum is 48, so the mean of this data set is 4.8. The mode of a data set is the value that occurs the most in a set. In this case, 2 occurs once, 4 occurs three times, 5 occurs three times, 6 occurs twice, and 7 occurs once, so the mode of this data set is both 4 and 5.
As a waitress, Willow earns an average of 19% tips on all food sales. Last week she worked three days and sold an average of $426.00 in food each day. How much did Willow earn in tips last week? (4 points)
$80.94
$102.54
$242.82
Answers
Answer:
$242.82
Step-by-step explanation:
Amadi is three times as old as Chima. The sum of their ages is 24
Answers
Answer:
Amadi: 20 years old
Chima : 4 years old
Simplify the following expression:-8 (5b + 2) -7 (6-5)-47b2+ 21-33b + 1933b - 19-47b-19
Answers
We have the following expression given:
\(-8(5b+2)-7(b-5)\)We can start simplifying the parenthesis and we got:
\(-40b-16-\left\lbrack 7b-35\rbrack\right\rbrack \)And we can distribute the signs :
\(-40b-16-7b+35\)Now we can aggrupate:
\((-40b-7b)+(35-16)\)And if we simplify we got:
\(-47b+19\)Here is a circle with a radius of 15 units whose center is (0,0) If the Y coordinate is 12, what is the x coordinate
Answers
In light of the query we've got Here's a circle whose center is at and whose radius is 15 units (0,0) The x-coordinate becomes 9 or -9 whereas if Y coordinate is 12.
What are diameter and radius?The distance between a circle's center and circumference is known as the radius. Always, the diameter is twice the radius. As a result, the ratio is created by multiplying the diameter by two.
According to the formula we get
\(x^2\) + \((y - 0)^2\) = \(15^2\)
Substituting the given values:
\(x^2\)+ \((12 - 0)^2 = 15^2\)
\(x^2\) + 144 = 225
\(x^2\)= 81
x = ±9
Therefore the x-coordinate will be 9 or -9.
To know more about Radius visit :
https://brainly.com/question/14618066
#SPJ1
24
A
Step 1
Algebra 1
1A: 2198 262 2A:
3A:
Topic 6-Quadratic Functions - Assessment 2 Retake A
4A:
Here is a pattern of squares.
2. Draw a diagram to show that 5(x+2) = 5x + 10.
Step 2
Step 3
3A: Write an expression for step n of this pattern:
2A: Is this pattern linear, exponential, or quadratic?
How do you know?
5A:
revenue (dollars)
1000
800
600
400
200
Name Marc burke
2 4 6 8 10 12 14 16 18 20
price (dollars)
Use the graph to answer the following question:
5A: What is the domain of this graph?
loodsholt tohut 69

Answers
The function of the sequence is T(n) = n² + n and it is quadratic
The domain of the graph is [0, 18]
The expression for the n-th termFrom the question, we have the following parameters that can be used in our computation:
Step Cells
1 2
2 6
3 12
From the table, we have
T(n) = n * (n + 1)
This gives
T(n) = n² + n
Hence, the function is T(n) = n² + n
The sequence typeThe sequence T(n) = n² + n is a quadratic sequence
The domain of the graphThis is the set of the x values
From the graph, we have
x = 0 to 18
So, we have
Domain = [0, 18]
Read more about sequence at
https://brainly.com/question/6561461
#SPJ1
In a sample of 800 U.S. adults, 171 dine out at a resaurant more than once per week. Two U.S. adults are selected at random from the population of all U.S. adults without replacement. Assuming the sample is representative of all U.S. adults.
Required:
a. Find the probability that both adults dine out more than once per week.
b. Find the probability that neither adult dines out more than once per week.
c. Find the probability that at least one of the two adults dines out more than once per week.
d. Which of the events can be considered unusual? Explain.
Answers
Answer:
a) 4.55% probability that both adults dine out more than once per week.
b) 61.80% probability that neither adult dines out more than once per week.
c) 38.20% probability that at least one of the two adults dines out more than once per week.
d) An event is considered unusual if it has a less than 5% probability of happening. Following this rule, in this problem, both adults dining out more than once per week can be considered unusual.
Step-by-step explanation:
The adults are selected without replacement, so we use the hypergeometric distribution to solve this question.
Hypergeometric distribution:
The probability of x sucesses is given by the following formula:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}*C_{N-k,n-x}}{C_{N,n}}\)
In which:
x is the number of sucesses.
N is the size of the population.
n is the size of the sample.
k is the total number of desired outcomes.
Combinations formula:
\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this question:
800 adults, so \(N = 800\)
171 dine out at a resaurant more than once per week, so \(k = 171\)
2 are chosen, so \(n = 2\)
a. Find the probability that both adults dine out more than once per week.
This is P(X = 2).
\(P(X = 2) = h(2,800,2,171) = \frac{C_{171,2}*C_{629,0}}{C_{800,2}} = 0.0455\)
4.55% probability that both adults dine out more than once per week.
b. Find the probability that neither adult dines out more than once per week.
This is P(X = 0).
\(P(X = 0) = h(0,800,2,171) = \frac{C_{171,0}*C_{629,2}}{C_{800,2}} = 0.6180\)
61.80% probability that neither adult dines out more than once per week.
c. Find the probability that at least one of the two adults dines out more than once per week.
Either none dines out more than once per week, or at least one does. The sum of the probabilities of these events is 100%. So
p + 61.80 = 100
p = 38.20
38.20% probability that at least one of the two adults dines out more than once per week.
d. Which of the events can be considered unusual? Explain.
An event is considered unusual if it has a less than 5% probability of happening. Following this rule, in this problem, both adults dining out more than once per week can be considered unusual.