Solve for x: 4 over 5 x + 4 over 3 = 2x x = Write your answer as a fraction in simplest form. Use the "/" symbol for the fraction bar. (2 points)
Answers
Answer:
x = 10/9
Step-by-step explanation:
Solve for x:
(4 x)/5 + 4/3 = 2 x
Put each term in (4 x)/5 + 4/3 over the common denominator 15: (4 x)/5 + 4/3 = (12 x)/15 + 20/15:
(12 x)/15 + 20/15 = 2 x
(12 x)/15 + 20/15 = (12 x + 20)/15:
(12 x + 20)/15 = 2 x
Multiply both sides by 15:
(15 (12 x + 20))/15 = 15×2 x
(15 (12 x + 20))/15 = 15/15×(12 x + 20) = 12 x + 20:
12 x + 20 = 15×2 x
15×2 = 30:
12 x + 20 = 30 x
Subtract 30 x from both sides:
(12 x - 30 x) + 20 = 30 x - 30 x
12 x - 30 x = -18 x:
-18 x + 20 = 30 x - 30 x
30 x - 30 x = 0:
20 - 18 x = 0
Subtract 20 from both sides:
(20 - 20) - 18 x = -20
20 - 20 = 0:
-18 x = -20
Divide both sides of -18 x = -20 by -18:
(-18 x)/(-18) = (-20)/(-18)
(-18)/(-18) = 1:
x = (-20)/(-18)
The gcd of 20 and -18 is 2, so (-20)/(-18) = (-(2×10))/(2 (-9)) = 2/2×(-10)/(-9) = (-10)/(-9):
x = (-10)/(-9)
Multiply numerator and denominator of (-10)/(-9) by -1:
Answer: x = 10/9
Related Questions
4-5 = x what is x-2? 5
Answers
The given expression is
\(\frac{4-5}{5}=x\)First, we solve the subtraction
\(\frac{-1}{5}=x\)Now we subtract 2 on each side to get x-2
\(-\frac{1}{5}-2=x-2\)Let's solve the difference
\(\begin{gathered} \frac{-1-10}{5}=x-2 \\ \frac{-11}{5}=x-2 \end{gathered}\)Therefore, x-2 is equal to -11/5.I WILL GIVE YOU BRAINLIEST!!!!!
Jack invests $30,000 with an interest rate of 4.5% compounded quarterly. After 6 years, what is the total amount of Jack's investment?
Enter your answer in the box rounded to the nearest cent.
Answers
Answer:
30,324
Step-by-step explanation:
30,000 x 4.5 = 135.00
135.00 x 4 + 540.00 four quarters in a year
6 years x 540 = 3,240
30,000 + 3,240 = 33. 240
Which expression is m.m.m.m.m rewritten in exponential form
Answers
Answer: M^5
Step-by-step explanation: M•M•M•M•M
Answer:
M^5
Step-by-step explanation:
M×M×M×M×M =M^5
The Olympiad task For the 10th grade if you do not know how to solve it immediately sayCorrect answer 2

Answers
Given:-
\(f(\frac{1}{x+1})=\frac{1}{2}f(x),f(1-x)=1-f(x)\)To find:-
\(s_n=f(1)+f(\frac{1}{2})+f(\frac{1}{3})+\cdots+f(\frac{1}{n})\)Now we simplify above equation to solve it,
\(\begin{gathered} f(1)+f(\frac{1}{2})+f(\frac{1}{3})+\cdots+f(\frac{1}{n})=f(1)+f(\frac{2-1}{2})+f(\frac{3-2}{3})+\cdots+f(\frac{n+1-n}{n}) \\ f(1)+f(\frac{1}{2})+f(\frac{1}{3})+\cdots+f(\frac{1}{n})=f(1)+f(1-\frac{1}{2})+f(1-\frac{2}{3})+\ldots+f(1-\frac{(n-1)}{n}) \\ f(1)+f(\frac{1}{2})+f(\frac{1}{3})+\cdots+f(\frac{1}{n})=f(1)+1-f(\frac{1}{2})+1-f(\frac{2}{3})+\cdots+1-f(\frac{n-1}{n}) \\ f(1)+f(\frac{1}{2})+f(\frac{1}{3})+\cdots+f(\frac{1}{n})=f(1)-f(\frac{1}{2})-f(\frac{2}{3})-\cdots-f(\frac{n-1}{n})+1(n-1) \\ f(1)+f(\frac{1}{2})+f(\frac{1}{3})+\cdots+f(\frac{1}{n})=f(1)-f(\frac{1}{1+1})-f(\frac{2}{2+1})-\cdots-f(\frac{n-1}{(n-1)+1})+1(n-1) \end{gathered}\)By furthur simplification we get,
\(\begin{gathered} f(1)-f(\frac{1}{1+1})-f(\frac{2}{2+1})-\cdots-f(\frac{n-1}{(n-1)+1})+1(n-1)=f(1)-\frac{1}{2}f(1)-\frac{1}{2}f(2)-\cdots-\frac{1}{2}f(n-1)+1(n-1)_{} \\ \text{ =}-\frac{1}{2}f(1)-\frac{1}{2}f(2)-\cdots-\frac{1}{2}f(n-1)+1(n-1) \\ \text{ =-}\frac{1}{2}\lbrack f(1)+f(2)+...+f(n-1)\rbrack+1(n-1) \end{gathered}\)So the requiired answer is,
\(\text{-}\frac{1}{2}\lbrack f(1)+f(2)+...+f(n-1)\rbrack+1(n-1)\)In a recent study on world happiness, participants were asked to evaluate their current lives on a scale from0 to 10, where 0 represents the worst possible life and 10 represents the best possible life. The meanresponse was 5.2 with a standard deviation of 2.4.(a) What response represents the 95th percentile?(b) What response represents the 60th percentile?(c) What response represents the first quartile?...
Answers
Solution
\(\begin{gathered} \text{Given} \\ \operatorname{mean},\text{ }\mu=5.2 \\ \text{standard deviation, }\sigma=2.4 \\ \\ \text{Recall the formula} \\ Z=\frac{x-\mu}{\sigma} \\ x-\mu=Z\sigma \\ x=Z\sigma+\mu \end{gathered}\)(a)
\(\begin{gathered} Z-\text{score for 95 percentile = 1.645} \\ x=Z\sigma+\mu \\ x=1.645(2.4)+5.2 \\ x=9.148 \\ x=9.15\text{ (2 decimal places)} \end{gathered}\)(b)
\(\begin{gathered} Z-\text{score for 60 percentile = }0.253 \\ x=Z\sigma+\mu \\ x=0.253(2.4)+5.2 \\ x=5.8072 \\ x=5.81\text{ (2 decimal places)} \end{gathered}\)(c)
\(\begin{gathered} Z-\text{score for first quartile (25\%) = }-0.674 \\ x=Z\sigma+\mu \\ x=-0.674(2.4)+5.2 \\ x=3.5824 \\ x=3.58\text{ (2 decimal places)} \end{gathered}\)Find the component form of the resultant vector.
f = (10,5)
v = (-3,-10)
Find: -f +v
Answers
Answer:
(-f+v) = -13i-15j
Step-by-step explanation:
Given that,
Vector f = (10,5) = 10i+5j
Vector v = (-3,-10) = -3i-10j
We need to find (-f+v).
Let x = (-f+v)
Plug all the values,
x = [-(10i+5j) + -3i-10j]
= (-10i-3i)+(-5j-10j)
= -13i-15j
Hence, (-f+v) = -13i-15j
Point s is on line segment rt. given rt = 19 and rs = 6, determine the length st
Answers
Under the consideration of collinearity of two line segments, the length of the line segment ST is equal to 13.
What is the length of a line segment collinear to another line segment?
According to the statement seen in this question, the line segments RT and ST are collinear to each other. Mathematically speaking, the length of the line segment ST can be found by using the following formula:
RT = RS + ST
ST = RT - RS
ST = 19 - 6
ST = 13
Under the consideration of collinearity of two line segments, the length of the line segment ST is equal to 13.
To learn more on line segments: https://brainly.com/question/25727583
#SPJ1
Write a possible equation for a cosine function that has a maximum point at (1, 11) and a minimum point at (8, 3).
Answers
M = A + |B| is the function's highest possible value. When sin or cos x equals 1, this maximum value is reached. m = A |B| is the function's lowest possible value. If either cos x or sin x is equal to 1, this minimum will be reached.
How do you find the maximum and minimum of a cosine function?The sine and cosine functions are graphed; to find the values of the sine and cosine functions for a variety of various degrees of angles, use a calculator, computer, or a collection of trigonometry tables (or radian).Because the sine and cosine functions have periods of 2, the patterns are continually repeated to the left and right.The sine and cosine functions can have a number of additional terms and factors added to them, changing how they look.The graph of the sine functions can be vertically shifted by adding the extra term A to the equation y = A + sin x. The sine function can have different amplitudes because to the additional element B in the equation y = B sin x. The graph's highest and minimum values, or one half of those values, make up the amplitude, or | B |, which is the maximum deviation from the x-axis. Both y = A + B sin x and y = A + B cos x are produced by combining these values. The minimum and maximum values for these two functions are specified by the following formulas. M = A + |B| is the function's highest possible value. When sin or cos x equals 1, this maximum value is reached. m = A |B| is the function's lowest possible value.If either cos x or sin x is equal to 1, this minimum will be reached.Example :
Draw the y = 1 + 2 sin x function on a graph. Which values represent the function's maximum and minimum?1 + 2 = 3 is the highest possible value. 1 + 2 = 1 is the minimum value.To Learn more About sin or cos refer To:
https://brainly.com/question/28160425
#SPJ1

Aron flips a penny 9 times. which expression represents the probability of getting exactly 3 heads? p (k successes) = subscript n baseline c subscript k baseline p superscript k baseline (1 minus p) superscript n minus k. subscript n baseline c subscript k baseline = startfraction n factorial over (n minus k) factorial times k factorial endfraction
Answers
The probability of getting exactly 3 heads when a penny is flipped 9 times is approximately 0.1641.
The expression that represents the probability of getting exactly 3 heads when a penny is flipped 9 times is:
p(3 successes) = (9 C 3) * (0.5)^3 * (0.5)^(9-3)
Where:
"p(3 successes)" represents the probability of getting 3 heads.
"9 C 3" represents the number of ways to choose 3 flips out of 9 flips (also known as the binomial coefficient). This is calculated as 9! / (3! * (9-3)!), which simplifies to 84.
"0.5" represents the probability of getting heads on a single flip of a fair penny.
"(0.5)^(9-3)" represents the probability of getting tails on the remaining 6 flips, since the probability of getting either heads or tails on a single flip is 0.5.
Simplifying the expression, we get:
p(3 successes) = (9 C 3) * (0.5)^9
p(3 successes) = (84) * (0.5)^9
p(3 successes) ≈ 0.1641
Therefore, the probability of getting exactly 3 heads when a penny is flipped 9 times is approximately 0.1641.
Learn more about "Probability" : https://brainly.com/question/23417919
#SPJ11
Rename each fraction as a whole number or mixed number SRB 171
Answers
3/5 = 0.6 or 3/5 as a fraction in its simplest form. 7/8 = 0.875 or 7/8 as a fraction in its simplest form. 2/3 = 0.666... or 2/3 as a fraction in its simplest form. 5/6 = 0.833... or 5/6 as a fraction in its simplest form. 1/4 = 0.25 or 1/4 as a fraction in its simplest form
To rename a fraction as a whole number or mixed number, we divide the numerator by the denominator. If the result is a whole number, then the fraction is renamed as that whole number. If the result is a mixed number, we take the integer part as the whole number and the fractional part as the numerator of the proper fraction. For example, 7/8 can be renamed as a mixed number by dividing 7 by 8, which gives 0.875. The integer part is 0, so we take the fractional part 0.875 as the numerator of the proper fraction. We can simplify it to 7/8. Similarly, we can rename the other fractions in the same way.
Learn more about fractions here: brainly.com/question/10354322
#SPJ4
Complete question:
Rename each fraction as a whole number or mixed number
3/5
7/8
2/3
5/6
1/4
Note: Angles not necessarily drawn to scale

Answers
Answer:
for finding x
x+133=180(being linear pair)
x=180-133
x=47 degree
Step-by-step explanation:
Answer:
47°
Step-by-step explanation:
→ Work out APD
133°
→ Find the sum of APC and DPB
360 - ( 133 + 133 ) = 94
→ Divide the answer by 2
94 ÷ 2 = 47°
prove that for each natural number n > 43, we can write n = 6xn 9yn 20zn 15. strong induction 117 for some nonnegative integers xn, yn, zn. then prove that 43 cannot be written in this form
Answers
For each natural number n > 43, we can express it as n = 6xn + 9yn + 20zn + 15, where xn, yn, and zn are nonnegative integers. Additionally, we have shown that 43 cannot be written in this form.
To prove that for each natural number n > 43, we can write n = 6xn + 9yn + 20zn + 15, where xn, yn, and zn are nonnegative integers, we will use strong induction. The base case will be n = 44, and we will assume that the statement holds for all natural numbers up to k, where k > 43. Then we will prove that it holds for k+1.
Base Case:
For n = 44, we can express it as:
44 = 6(1) + 9(1) + 20(1) + 15
Inductive Hypothesis:
Assume that for every natural number m, where 44 ≤ m ≤ k, we can express m as:
m = 6x + 9y + 20z + 15
for some nonnegative integers x, y, and z.
Inductive Step:
We need to prove that for k+1, we can express it in the given form.
For k+1, there are three cases to consider:
Case 1: k+1 is divisible by 6
In this case, we can express k+1 as:
(k+1) = 6x' + 9y' + 20z' + 15
where x' = x + 1, y' = y, and z' = z. Since k+1 is divisible by 6, we can add one more 6 to the expression.
Case 2: k+1 is divisible by 9
In this case, we can express k+1 as:
(k+1) = 6x' + 9y' + 20z' + 15
where x' = x, y' = y + 1, and z' = z. Since k+1 is divisible by 9, we can add one more 9 to the expression.
Case 3: k+1 is not divisible by 6 or 9
In this case, we can express k+1 as:
(k+1) = 6x' + 9y' + 20z' + 15
where x' = x + 2, y' = y + 1, and z' = z - 1. By adding 26, 19, and subtracting 1*20, we can obtain k+1.
Thus, we have shown that for each natural number n > 43, we can write n = 6xn + 9yn + 20zn + 15, where xn, yn, and zn are nonnegative integers.
Now, let's prove that 43 cannot be written in this form. If we assume that 43 can be expressed as:
43 = 6x + 9y + 20z + 15
Simplifying the equation:
28 = 6x + 9y + 20z
Considering the equation modulo 3, we have:
1 ≡ 0 (mod 3)
This is a contradiction since 1 is not congruent to 0 modulo 3. Therefore, 43 cannot be written in the given form.
In conclusion, we have proven by strong induction that for each natural number n > 43, we can express it as n = 6xn + 9yn + 20zn + 15, where xn, yn, and zn are nonnegative integers. Additionally, we have shown that 43 cannot be written in this form.
Learn more about natural number here
https://brainly.com/question/28567528
#SPJ11
help me with maths pls

Answers
After answering the given query, we can state that the solutions to the simultaneous equations are (x, y) ≈ (3.1, 10.2) and (x, y) ≈ (-1.9, 0.2).
What is a linear equation?In mathematics, a linear equation has become one that takes the form y=mx+b. The inclination is B, and the y-intercept is m. Since y and x are variables, the preceding clause is frequently referred by the term a "linear equation involving two variables."
Bivariate linear equations are linear equations with two variables. Linear equations can be found in many places, including 2x - 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, and 3x - y + z = 3. When the formula has the structure y=mx+b, where m denotes the slope and b the y-intercept, it is often referred to because of being quadratic.A mathematical equation is said to be linear if its solution has the form y=mx+b, where m stands for the slope and b for the y-intercept.
To show that 3y² - 10y - 24y¯47 = O, we need to find constants C and k such that |3y² - 10y - 24y¯47| ≤ C|y| for all y > k.
3y² - 10y - 24y¯47 ≤ 3y² + 10|y| + 24
3y² + 10|y| + 24 ≥ 3y² - 10y - 24y¯47 for y ≥ 5
C = 6:
|3y² - 10y - 24y¯47| ≤ 6|y| for y ≥ 5
3y² - 10y - 24y¯47 = O.
b) Using the result from part a), we can rewrite the simultaneous equations as:
3y² - 10y - 24y¯47 = O
y - 2x = 4
y = 2x + 4
3(2x + 4)² - 10(2x + 4) - 24y¯47 = O
12x² - 8x - 79 = O
x = (8 ± √(8² + 41279))/24
x ≈ 3.1 or x ≈ -1.9
y ≈ 10.2 or y ≈ 0.2
Therefore, the solutions to the simultaneous equations are (x, y) ≈ (3.1, 10.2) and (x, y) ≈ (-1.9, 0.2).
To know more about linear equation visit:
brainly.com/question/11897796
#SPJ1
What is the simplified form of the rational expression below?
5x -5
3x + 3x
А.5(x + 1)
3x
B. 5(x+1)
3
c. 5(x=1)
3
D. 5(x - 1)
3x
Answers
Answer:
A
Step-by-step explanation:
I can put explanation in the comments
Elmer spent the day at the mall. First, he bought five rabbits for $10 each. Later, he bought four cupboards for $70 each. After that, he found a twenty dollar bill. Also, he returned one rabbit. Write the total change to Elmer's funds as an integer.
Answers
Answer:
-300
Step-by-step explanation:
Step 1: Find the amount Elmer's funds decreased after purchasing the rabbits:
Let x represent Elmer's funds.
Since Elmer bought five rabbits for $10 each, he lost $10 5 times.
x - (10 * 5)
x - 50
Thus, Elmer lost (spent) $50 for the 5 rabbits.
Step 2: Find the amount Elmer's funds decreased after purchasing the cupboards:
Since Elmer bought four cupboards for $70 each, he lost $70 4 times:
x - (50 + (70 * 4))
x - (50 + 280)
x - 330
Thus, after purchasing the rabbits and cupboards, Elmer lost $330.
Step 3: Find the amount Elmer's funds increased after finding the twenty-dollar bill:
Since Elmer found a twenty-dollar bill, he gained $20
x - (330 + 20)
x - 310
Step 4: Find the amount Elmer's funds increased after returning one rabbit:
Since Elmer returned one rabbit, he gained $10:
x - (310 + 10)
x - 300
Thus, Elmer's funds changed totally by -$300.
Putting all the information together, we have:
x - 10 - 10 - 10 - 10 - 10 - 70 - 70 - 70 - 70 + 20 + 10
x - 50 - 280 + 30
x - 330 + 30
x - $300
What is the exponential of 1?
Answers
Exponential of 1 is equal to the number itself which means 1.
Exponent is usually described as the method of demonstrating large numbers in terms of powers. It means, exponent refers to the count, that how many times a number is multiplied to itself to calculate that exponent.
In accordance with the exponent rule, any number raised to power of 1 would always be equal to 1 that is because it doesn't matter how many times we multiply 1 to itself. It is going to yield 1. For example, multiplying 1 hundred times i.e. 1^100 also results in 1.
For further information about exponents, click the link below:
brainly.com/question/15438343
#SPJ4
What is 7 (x+3) -7 = y simplified
Answers
Answer:
7 (x+3) -7 = y
7x+21-7=y
7x+14=y
ok so like I need helpp ;-;

Answers
Answer:
i think the answer is B because 3/4 is more than 2/3
Answer:
its b.
Step-by-step explanation:
if you convert them, so they both have the same dominator, nadias recipe ends up needing more flour.
A flat rate shipping box is in the shape of a rectangular prism you estimate the volume of the box 350 in.³ you measure the box and find that has a length of 10 inches a width of 9 inches and a height of 4.5 inches find the percent error round your answer to the nearest 10th of a percent
Answers
Answer:14.4
Step-by-step explanation:
7. Hannah invests £750 and after 4 years has £844.13. Find the compound interest rate.
Answers
If the amount after 4 years is 844.13. Then the rate of the compound interest will be 3%.
What is compound interest?A loan or deposit's interest is computed using the starting principle and the interest payments from the ago decade as compound interest.
We know that the compound interest is given as
A = P(1 + r)ⁿ
Where A is the amount, P is the initial amount, r is the rate of interest, and n is the number of years.
Hannah contributes £750 and following 4 years has £844.13. Then the compound interest rate is given as,
844.13 = 750 (1 + r)⁴
(1 + r)⁴ = 1.1255
1 + r = 1.02999
r = 0.0299
r = 2.99%
r ≈ 3%
If the amount after 4 years is 844.13. Then the rate of the compound interest will be 3%.
More about the compound interest link is given below.
https://brainly.com/question/25857212
#SPJ1
please help I don't get it

Answers
2. Using proportion, the value of x = 38, the length of FC = 36 in.
3. Applying the angle bisection theorem, the value of x = 13. The length of CD = 39 cm.
What is the Angle Bisector Theorem?The Angle Bisector Theorem states that in a triangle, an angle bisector divides the opposite side into segments that are proportional to the lengths of the other two sides of the triangle.
2. The proportion we would set up to find x is:
(x - 2) / 4 = 27 / 3
Solve for x:
3 * (x - 2) = 4 * 27
3x - 6 = 108
3x = 108 + 6
Simplifying:
3x = 114
x = 114 / 3
x = 38
Length of FC = x - 2 = 38 - 2
FC = 36 in.
3. The proportion we would set up to find x based on the angle bisector theorem is:
13 / 3x = 7 / (2x - 5)
Cross multiply:
13 * (2x - 5) = 7 * 3x
26x - 65 = 21x
26x - 21x - 65 = 0
5x - 65 = 0
5x = 65
x = 65 / 5
x = 13
Length of CD = 3x = 3(13)
CD = 39 cm
Learn more about Angle Bisector Theorem on:
https://brainly.com/question/30459648
#SPJ1
HELP QUICK PLEASE! I NEED HELL ASAP PLEASEEE!!!

Answers
Step-by-step explanation:
I have solved the your question Above

how many of u are from India
Answers
Answer:
I was born in California and then moved to Texas bt Im indian because my parents are indian
five times the square of a number
Answers
The expression is 5 * n².
What is an Expression?An expression is a mathematical statement that consists of variables, constants and mathematical operators.
The representation of a quantity in terms of a value is done by a number.
There are various types of numbers like real numbers, natural numbers, whole numbers, rational numbers, etc.
The expression is :
Five times the square of a number
Let the number be n, then
5 * n²
Let n =1
The value of the expression will be
5 * (1)² = 5
Let n = 2
The value of the expression will be
5 * (2)²
5 * 4
20
Let n = 5
5 * (5)²
5 * 25
125
Let n = 100
5 * (100)²
5 * 10000
50000
To know more about Expression
https://brainly.com/question/14083225
#SPJ1
Classify the polygon by its number of sides. State whether the polygon appears to be regular or not regular it’s has 8 sides

Answers
Answer:
octagon, regular
Step-by-step explanation:
it has eight sides and the side all measure the same amount
how can knowledge of circles apply to daily life??
Answers
Answer:
sdgsdgsdgsdgsdgsd
Step-by-step explanation:
gsdgsdgsdgsdgsd
please help me with question 21

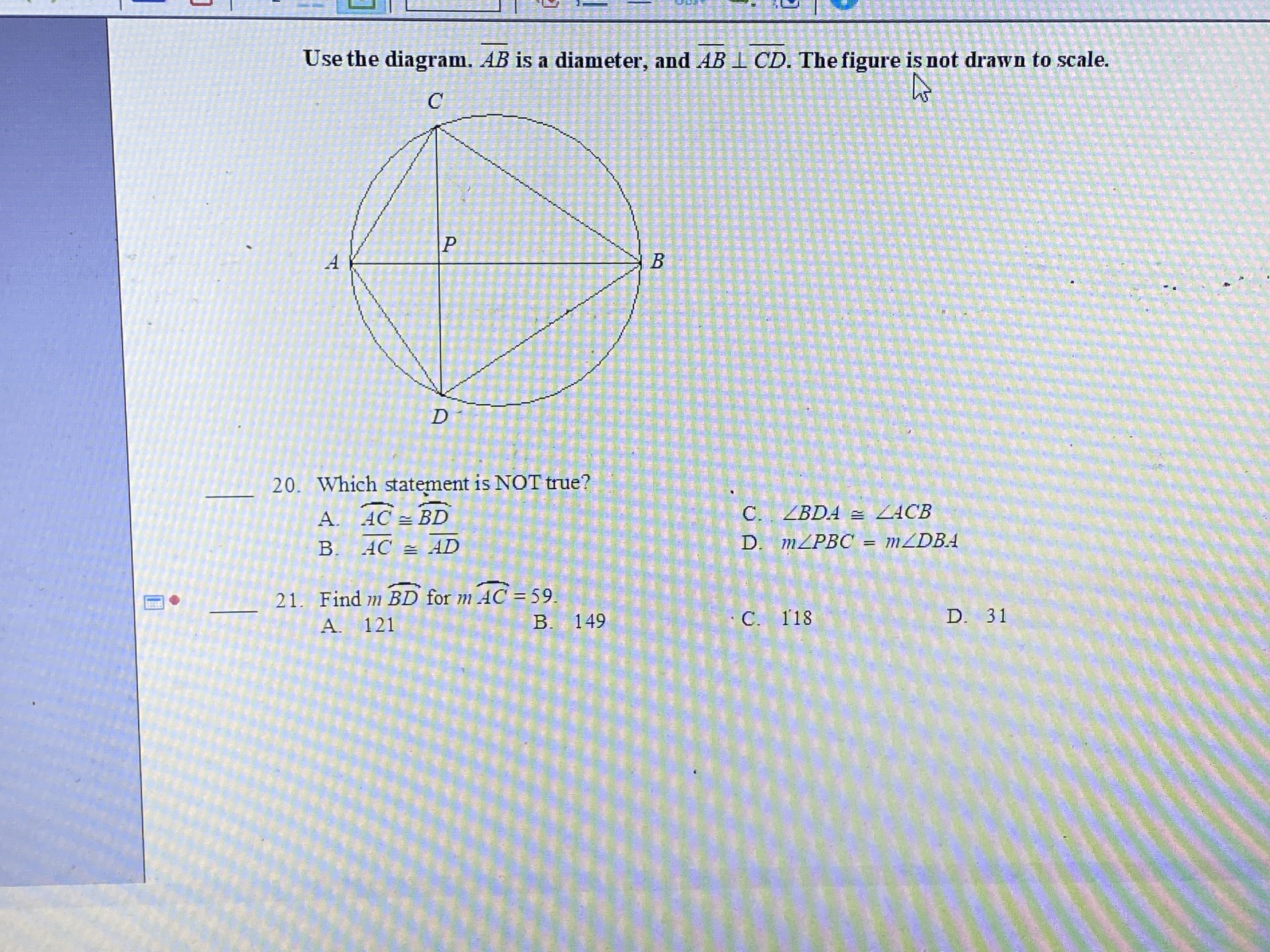
Answers
Using the central angle theorem, we can find the arm length of BD to be 118units.
Option C is correct.
Define central angle theorem?The angle that an arc occupies at the centre of a circle is twice as large as the angle it occupies anywhere else around the circle's circumference, according to the central angle measure theorem.
Here in the question,
Length of the arc AC = 59.
As we can see that there is a quadrilateral inscribed inside the circle.
Arc AC = 1/2 arc BD
⇒ arc BD = 2 × arc length AC
⇒ arc BD = 2 × 59
⇒ arc BD = 118.
Therefore, the length of the arc BD = 118 units.
To know more about central angle, visit:
https://brainly.com/question/15698342
#SPJ1
Using the central angle theorem, we can find the arm length of BD to be 118units.
Option C is correct.
Define central angle theorem?The angle that an arc occupies at the centre of a circle is twice as large as the angle it occupies anywhere else around the circle's circumference, according to the central angle measure theorem.
Here in the question,
Length of the arc AC = 59.
As we can see that there is a quadrilateral inscribed inside the circle.
Arc AC = 1/2 arc BD
⇒ arc BD = 2 × arc length AC
⇒ arc BD = 2 × 59
⇒ arc BD = 118.
Therefore, the length of the arc BD = 118 units.
To know more about central angle, visit:
https://brainly.com/question/15698342
#SPJ1
A single pump can add only 0.35 pound of air into a bicycle tire. The bicycle tire will hold a maximum of 640 ounces of air per square inch. How many pumps are required to inflate the bicycle tire to maximum pressure?
A.15 pumps
B. 115 pumps
C. 225 pumps
D. 1,829 pumps
Answers
The bicycle tire needs an amount of 115 pumps to be fully inflated. (Correct choice: B)
How many pumps are required to inflate the bicycle tire to maximum pressure
In this problem we need to determine the number of pumps needed to inflate the bicycle tire at maximum pressure, this number (n) is equal to the maximum capacity of the tire (V), in ounces, and the mass added by a single pump (p), in ounces:
n = V / p
If we know that V = 640 oz and p = 5.6 oz (1 lb = 16 oz), then the number of pumps is:
n = 640 oz / 5.6 oz
n = 114.286
n = 115
An amount of 115 pumps are needed to inflate the bicycle tire to maximum pressure.
To learn more on bicycle tires: https://brainly.com/question/17236210
#SPJ1
Jamal is 12 years older than twice Stephanie’s age. The sum of their ages is 45. A. If Stephanie’s age is represented by x, write an expression for Jamal’s age in terms of Stephanie’s age. _________________________ B. Write an equation that you can use to find the ages of both Stephanie and Jamal. Solution: ________________ D. Stephanie’s age: ___________ Jamal’s age: PLEASE PLEASE HELPPPP IMPORTANNNTTTT
Answers
Answer:
Jamal's age = 2×x+12= 2x+12
sum og ages = 45
2x+12+x= 45
=3x+12=45
=45-12= 3x
= 32=3x
x= 32/3= 10.67
2x+13 =21.34+12= 33.34
hope.ot helps
plz mark as brainliest
The perimeter of an equilateral triangle with side length s is 3s. Leslie is using a wooden equilateral triangle with 15-inch sides as a stand for her newest sculpture.
What is the perimeter of the stand?