solve for x 3x+10 3x -28 will mark brainest answers are 1. 33 2. 34 3. 35 4. 36 ty so much 1 left godbless

Answers
Answer:
1. x = 33Step-by-step explanation:
3x+10 + 3x -28 = 180
3x + 3x = 180 + 28 - 10
6x = 198
x = 198/6
x = 33
Answer:
33
Step-by-step explanation:
By the same side interior angle theorem, we can find that 3x + 10 and 3x - 28 are supplementary. Knowing this, we can make the equation:
(3x + 10) + (3x - 28) = 180
Now we can solve for x. Combine like terms.
6x - 18 = 180
Add 18 from both sides.
6x = 198
Divide both sides by 6.
x = 33
So the value of x would be 33.
I hope you find my answer and explanation to be helpful. Happy studying.
Related Questions
Plss answer I give you branlistb

Answers
2) 132
3) 1
4) 4
5) 12
What is the following product?
√12 √18
O√30
O 5√6
O 6√5
O 6√6
Answers
Answer: \(6\sqrt{6}\)
Step-by-step explanation:
\(\sqrt{12}=2\sqrt{3}\\\\\sqrt{18}=3\sqrt{2}\\\\\implies \sqrt{12} \sqrt{18}=2\sqrt{3}(3\sqrt{2}=\boxed{6\sqrt{6}}\)
The product of square root of 12 i.e.,√12 and square root of 18 i.e.,√18 is 6√6.
What is product law for exponent?When two numbers has equal power then we can multiply the the numbers and the power remains same. The number in the power is called exponent and the number is called as base. In \(a^m\), \(m\) is the exponent and \(a\) is the base of the number \(a^m\).
Step-by-step explanation:
\(\sqrt{12}\)\(=\sqrt{4}\)×\(\sqrt{3}\)\(=2\)×\(\sqrt{3}\) , since the square root of 4 is 2
\(\sqrt{18}=\sqrt{2}\)×\(\sqrt{9}\)\(=\sqrt{2}\)×\(3\) , since the square root of 9 is 3
Now, \(\sqrt{12} \sqrt{18} = 2\)×\(3\)×\(\sqrt{2}\)×\(\sqrt{3}\) from above.
\(=6\sqrt{6}\)
Hence the product of √12 and √18 is √12√18=6√6
To learn more about exponents click here:
https://brainly.com/question/27938922
#SPJ5
How can you determine if an equation will have:
One solution
No solution
Infinitely many solutions
Answers
9514 1404 393
Answer:
look at the reduced form:
0 = variable + constant (one solution)0=0 (infinite solutions)0=1 (no solutions)Step-by-step explanation:
We assume the question is concerned with linear equations in one variable.
Subtract one side of the equation from both sides, and simplify as far as possible. You will get one of three forms:
variable + constant = 0 . . . . has one solution
0 = 0 . . . . has infinitely many solutions
0 = 1 . . . . has no solutions
For exercises 7-9 write expressions for the area of each rectangle in two different ways. Then find the area using each expressions.
Answers
Answer:
No Questions are shown here
Step-by-step explanation:
Just says "For exercises, 7-9 write expressions for the area of each rectangle in two different ways. Then find the area using each expression."
25 is 36% of what number
Answers
Answer:
x = 69.44
Step-by-step explanation:
We have, 36% × x = 25
or, 36/100 × x = 25
Multiplying both sides by 100 and dividing both sides by 36,
we have x = 25 × 100/36
x = 69.44
If you are using a calculator, simply enter 25×100÷36, which will give you the answer.
Evaluate the given expression for x=5

Answers
x² + 3x - 2
(5)² + 3 × 5- 2
25 + 15 - 2
40 - 2
38...
Melanie runs 5miles a day. How many miles will her brother run in one week?
Answers
What is the value of x?
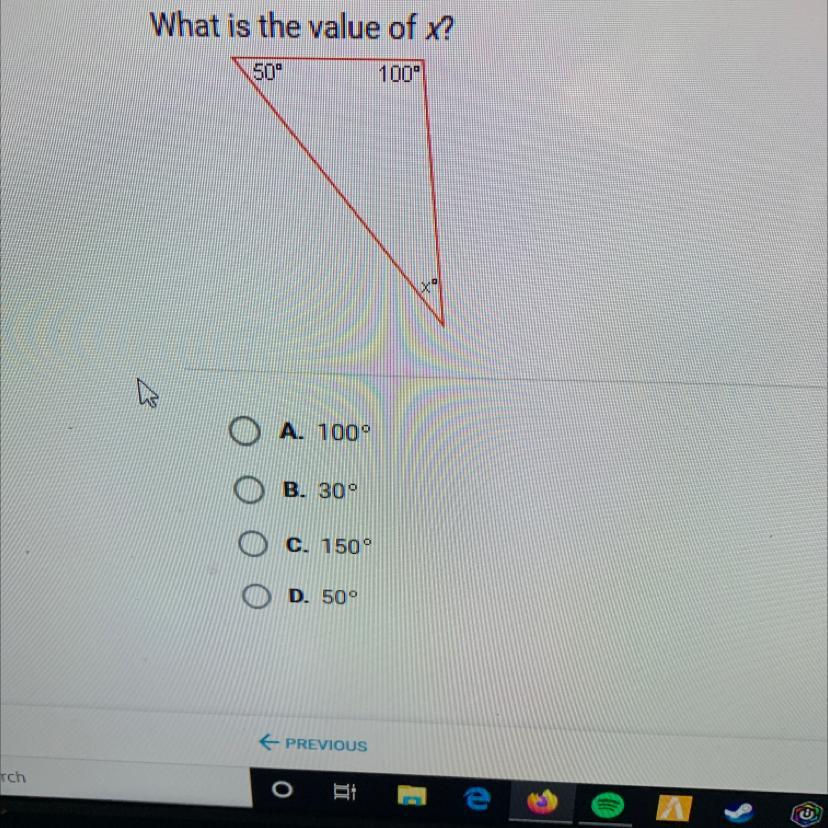
Answers
Answer:
The answer is 30 degrees
Step-by-step explanation:
the total of all three angles in a triangle add up to 180.
50+100= 150
so,
180-150= 30
x= 30 degrees
hope this helps!!
Answer:
answer is B 30
Step-by-step explanation:
180 is the total degrees of the whole thing subtract both angels they already give you (100+50) that leaves you with 30
Please show your work or you wont get brainly. I need this done as soon as possible, ty

Answers
Answer:97/12 + (-4 1/3) = 15/4
Step-by-step explanation:
15/4 - (-4 1/3) = 97/12
97/12 + (-4 1/3) = 15/4
What is the slope of y = 1/5x - 3
Answers
Answer:
ITS 15 THANK ME LATER!!!!
Step-by-step explanation:
Answer:
M = 1/5
Step-by-step explanation:
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

luck is preparing food for his dog he mixes 3 cup of dry food and some cup of wet food he put all the food into 4 bowls he puts 5/4 cups into each bowl
Answers
To find the amount of wet food Luck mixed with the dry food, we can use the fact that he put 5/4 cups into each of the 4 bowls. Therefore, he used a total of 5/4 x 4 = 5 cups of wet food.
Thus, Luck mixed 3 cups of dry food and 5 cups of wet food to prepare the dog's meal.
Expand and Simplify Fully
5(2k+2)+3(K-5)
Answers
Answer:
\(13k - 5\)
Step-by-step explanation:
\(5(2k + 2) + 3(k - 5) = 10k + 10 + 3k - 15 \\ = 13k - 5\)
the usher at a wedding asked each of the 808080 guests whether they were a friend of the bride or of the groom. here are the results
Answers
The probability that a randomly selected person from this sample was a friend of the bride OR of the groom is 0.9875.
Given that, at a wedding each guest asked the 80 guests whether they were a friend of the bride or of the groom.
What is the probability?
Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event.
Total Number of Guests which forms the Sample Space, n(S)=80
Let the event (a friend of the bride) =A
Let the event (a friend of the groom) =B
n(A) =59
n(B)=50
Friends of both bride and groom,
So,
n(A∪B)=n(A)+n(B)-n(A∩B)
n(A∪B)=59+50-30
n(A∪B)=79
The number of Guests who was a friend of the bride OR of the groom = 79
Thus,
P(A∪B)=n(A∩B)/n(S)
= 79/80
= 0.9875
Hence, the probability that a randomly selected person from this sample was a friend of the bride OR of the groom is 0.9875.
To learn more about the probability visit:
brainly.com/question/11234923.
#SPJ4
what two numbers add to the number 30
Answers
Answer:
15+15
Step-by-step explanation:
Two 15's added together can equal 30
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
,
,
Answers
The x-coordinates where the graphs of the equations intersect are x = -1 and x = 3
How to determine the x-coordinates where the graphs of the equations intersect?From the question, we have the following parameters that can be used in our computation:
y = 2x
y = x² - 3
The x-coordinates where the graphs of the equations intersect is when both equations are equal
So, we have
x² - 3 = 2x
Rewrite the equation as
x² - 2x - 3 = 0
When the equation is factored, we have
(x + 1)(x - 3) = 0
So, we have
x = -1 and x = 3
Hence, the x-coordinates are x = -1 and x = 3
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Question
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
y = 2x
y = x² - 3
find the equation of the line that passes through the points (-3,-7) (-3,10
Answers
The equation of the line that passes through point (-3,-7) and point (-3,10) is x = -3.
What is the equation of the line passing through the given coordinates?The formula for equation of line is expressed as;
y = mx + b
Where m is slope and b is y-intercept.
Given the points through which the line passes: (-3,-7) and (-3,10).
The two given points (-3, -7) and (-3, 10) have the same x-coordinate -3
Hence, the two lines lie on a vertical line.
since the slope of the vertical line is undefined.
The equation of the line passing through these two points is simply the equation of the vertical line:
x = -3
Learn more about equation of line here: brainly.com/question/2564656
#SPJ1
Please help, thanks!

Answers
The change in function values is f(40) - f(10) = 49 - 55 = -6.
The change in x-values is 40 - 10 = 30.
Therefore, the average rate of change is -6/30, which simplifies to -1/5.
The average rate of change of the function over the interval 10 < x ≤ 40 is -1/5.
what is 11/4 times 4/9
Answers
Answer: 11/9
Step-by-step explanation:
you would cross out the two 4s(using butterfly method) and make them 1s. So 11 x 1 and 1 x 9 = 11/9
Answer:
11/4 times 4/9 is 11/9
Step-by-step explanation:
We have to find,
(11/4) times 4/9
\((11/4)(4/9) = (11*4/4*9)\)
We can cancel the 4s from the numeratorand denominator to get,
\((11*4/4*9) = (11*1/1*9) = 11/9\\=11/9\)
The answer is 11/9
Make frequency tables for the following data sets. Include columns for relative frequency. Also, make a bar graph for the frequency
Final grades of 30 students in a math class: AAAAAABBBBBBCCCCCCCCCCFFF
Answers
Hello everyone-SOLVING nonlinear system of equations- ALGEBRA 1

Answers
The solution to the nonlinear system of equations is (x, y) = (-3, -2) and (x, y) = (1, 6). These points represent the coordinates where the two equations intersect and satisfy both equations simultaneously.
To solve the nonlinear system of equations:
Equation 1: \(y = -x^2 + 7\)
Equation 2: y = 2x + 4
We can equate the right sides of both equations since they both represent y.
\(-x^2 + 7 = 2x + 4\)
To simplify the equation, we can rearrange it to be in the standard quadratic form:
\(x^2 + 2x - 3 = 0\)
Now, we can solve this quadratic equation by factoring, completing the square, or using the quadratic formula. In this case, let's use factoring:
(x + 3)(x - 1) = 0
From this equation, we get two possible solutions:
x + 3 = 0 => x = -3
x - 1 = 0 => x = 1
Now, we substitute these x-values back into either equation to find the corresponding y-values.
For x = -3:
y = 2(-3) + 4
y = -6 + 4
y = -2
For x = 1:
y = 2(1) + 4
y = 2 + 4
y = 6
For more such questions on coordinates
https://brainly.com/question/29660530
#SPJ8
Can you please help me

Answers
B. (The second one) x ≤ -3
What is the slope of a line that is perpendicular to the line 3y - 4x = -8?
Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\(3y - 4x = - 8\)
Add sides 4x
\(3y - 4x + 4x = 4x - 8\)
\(3y = 4x - 8\)
Divide sides by 3
\( \frac{3}{3} y = \frac{4}{3} x - \frac{8}{3} \\ \)
\(y = \frac{4}{3} x - 8 \\ \)
This is the slope-intercept form of the line.
We that the coefficient of the x in slope-intercept form , is the slope of the line.
Thus ;
\(slope = \frac{4}{3} \\ \)
_________________________________
Remember from now on ;
Multiply of the slopes of the lines which are perpendicular to each other equal -1 .
Suppose the slope of the line which question asked is m.
So :
\( \frac{3}{4} \times m = - 1 \\ \)
Multiply sides by 4
\(4 \times \frac{3}{4} \times m = 4 \times ( - 1) \\ \)
\(3m = - 4\)
Divide sides by 3
\( \frac{3}{3} m = \frac{ - 4}{3} \\ \)
\(m = - \frac{4}{3} \\ \)
Done...
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
How many grams are there in 37 kilograms?
Answers
there are 37,000 grams in 37 kilograms.
hope this helped! have a good day!
Answer:
37000
Step-by-step explanation:
Formula: multiply the mass value by 1000
37 *1000= 37000
On Sunday, Christina's savings account balance was $315.12.
On Monday,
she withdraws $78.95 and $143.80. She deposits
$63.29 on Tuesday. What is her balance after the deposit?
Answers
$315.12- $78.95- $143.80 + $63.29
Find the solution to the system of equations 2x + y = 3 and x - y = 3.
O (-2,1)
O (2,-1)
Please help me ..
Answers
Answer:
(2, - 1 )
Step-by-step explanation:
2x + y = 3 → (1)
x - y = 3 → (2)
adding the 2 equations term by term will eliminate y
3x + 0 = 6
3x = 6 ( divide both sides by 3 )
x = 2
substitute x = 2 into either of the 2 equations and solve for y
substituting into (1)
2(2) + y = 3
4 + y = 3 ( subtract 4 from both sides )
y = - 1
solution is (2, - 1 )
2(2)+(-1)=3
4+(-1)=3
3=3
and
2-(-1)=3
2+1=3
3=3
HELP ASAPPP! I WILL GIVE BRAINLIEST!
PICTURE BELOW.
PLEASE DO NOT PUT ANY NONE RELATED ANSWERS OR YOU WILL BE REPORTED !!

Answers
Answer:
Polygon A: A, D, E
Polygon B: F, G, H
Polygon C: K, L, M, N, O
Polygon D: S, T
Step-by-step explanation:
A 12 oz soda costs $1.25 in the vending machine. At that rate, how much would a
48 oz soda cost?
Answers
Answer:
$5
Step-by-step explanation:
48/12=4
1.25x4=5
Or you could set it up as a proportion
12/1.25=48/x
AABC is dilated by a factor of 2 to produce ▲A'B'C'. Which statement is not true? 62⁰ 34 16 A 28° 30
Answers
The statement that is not true is (a) A = 74 degrees
How to determine which statement is not true?From the question, we have the following parameters that can be used in our computation:
The dilation of ABC by a scale factor of 2
This means that
Scale factor = 2
The general rule of dilation is that
Corresponding sides are similar i..e they have the same ratioCorresponding angles are equalusing the above as a guide, we have the following:
AC = 2 * 5 = 10
C = 53 degrees
BC = 2 * 3 = 6
A = 37 degrees
Hence, the statement that is not true is (a) A = 74 degrees
Read more about dilation at
https://brainly.com/question/3457976
#SPJ1

his mapping shows a functional relationship. A mapping diagram shows a relation, using arrows, between domain and range for the following ordered pairs: (2, 4), (negative 3, 0), (negative 1, negative 1), (4, 3). When f(x)=4, what is the value of x? 0 2 3 4
Answers
when f(x)=4, then the value of x is 2
What is a function?A relation is a function if it has only One y-value for each x-value.
Given that A mapping diagram shows a relation, using arrows, between domain and range for the following ordered pairs:
The ordered pairs are (2, 4), (-3, 0), (- 1, -1), (4, 3)
We need to find value of x when f(x)=4
In the (x, y) ordered pair the x place represents the domain value and y place represents the range.
In the order pairs we have to look for the y value which has 4.
The corresponding element of 4 is the x value
So the value of x is 2 if f(x)=4
Hence, when f(x)=4, then the value of x is 2
To learn more on Functions click:
https://brainly.com/question/21145944
#SPJ1