solve for g:2(g-h)=b+4
Answers
Answer:
\(g = \frac{b}{2} + 2 + h\)
Step-by-step explanation:
\(2(g - h) = b + 4 \\g - h = \frac{b}{2} + \frac{4}{2}\\g = \frac{b}{2} + 2 + h\)
Related Questions
On a test called the MMPI-2, a score of 30 on the Anxiety Subscale is considered
very low. Felipe participates in a yoga group at his gym and decides to give this
subscale to 18 people in his yoga group. The mean of their scores is 35.2, with a standard deviation of 10.4. He wants to determine whether their anxiety scores are statistically equal to 30.
What are the groups for this one-sample t-test?
What is the null hypothesis for this one-sample t-test?
What is the value of "?
Should the researcher conduct a one- or two-tailed test?
What is the alternative hypothesis?
What is the value for degrees of freedom?
What is the t-observed value?
What is(are) the t-critical value(s)?
Based on the critical and observed values, should Felipe reject or retain the null
hypothesis? Does this mean that his yoga group has scores that are above 30, below 30, or
statistically equal to 30?
What is the p-value for this example?
What is the Cohen’s d value for this example?
If the " value were dropped to .01, would Felipe reject or retain the null hypothesis?
Calculate a 42% CI around the sample mean.
Calculate a 79% CI around the sample mean.
Calculate a 95% CI around the sample mean.
Answers
The MMPI-2 test is used for the assessment of psychopathology and personality of patients.
It includes 567 true-false questions, resulting in 10 clinical scales, among which one is the anxiety subscale.
A score of 30 or less is usually considered very low.
The questions are answered by the patient, usually in a clinical or research setting.
A one-sample t-test is conducted in the problem, whereby a sample of 18 participants in a yoga group is tested for anxiety scores.
The following are the parameters of the one-sample t-test:Groups:
18 participants
Null hypothesis: The anxiety scores of Felipe's yoga group are statistically equal to 30." value: 30
Type of test: One-tailed test
Alternative hypothesis: The anxiety scores of Felipe's yoga group are greater than 30.
Degrees of freedom: n - 1 = 17T-observed value: (35.2 - 30) / (10.4 / sqrt(18)) = 2.41T-critical value: 1.734
Reject or retain null hypothesis: Since the t-observed value (2.41) is greater than the t-critical value (1.734), Felipe should reject the null hypothesis, which implies that his yoga group's scores are greater than 30.P-value: 0.014Cohen’s d value: (35.2 - 30) / 10.4 = 0.5
If the " value were reduced to 0.01, Felipe would still reject the null hypothesis, since the p-value (0.014) is lower than the alpha level (0.01).
For the sample mean: 35.2CI for 42%: 35.2 ± 0.58CI for 79%: 35.2 ± 1.16CI for 95%: 35.2 ± 2.13
To know more about Degrees of freedom click here:
https://brainly.com/question/32093315
#SPJ11
What is the algebra expression for 4 minus the sum of a number and 6
Answers
Answer:
(x+6)-4
Step-by-step explanation:
Classify the triangle shown by sides and angles.
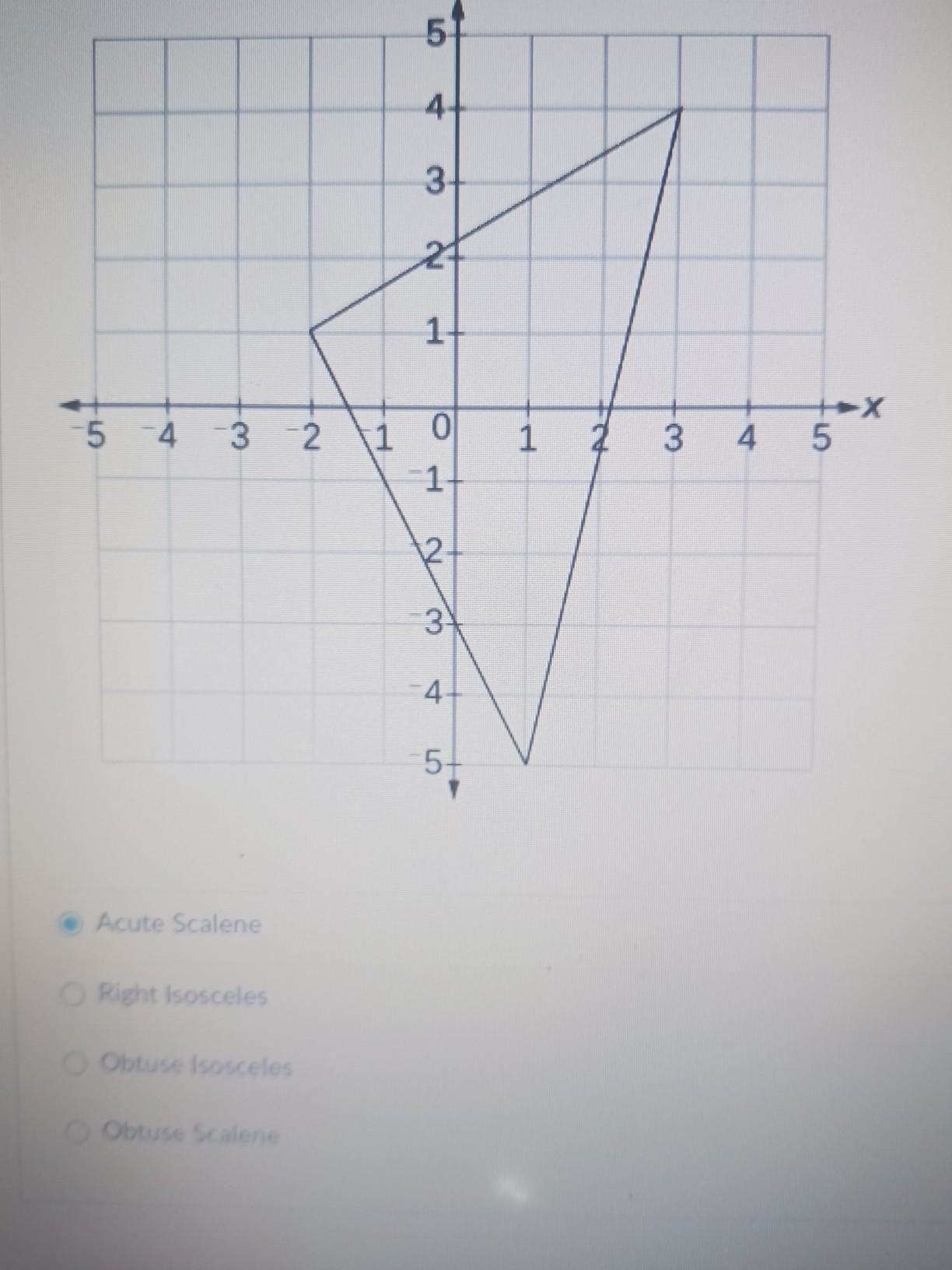
Answers
Answer:
Acute Scalene Triangle
Step-by-step explanation:
Look at all three angles of the triangle they are all acute. In addition, all of the angles on the triangle are different making it scalene.
please help asap will give brainliest thank you

Answers
Answer:
Thus, angle 2 = angle 4 = 76
Step-by-step explanation:
Step-by-step explanation:
Here, we want to get the measures of angle 2 and angle 4
From what we have in the diagram, angle 2 and angle 5 are supplementary (meaning they add up to 180)
The reason for this is because both angles are same side interior angles
Thus,
angle 2 + angle 5 = 180
angle 2 = 180 - angle 5
angle 2 = 180 -104
angle 2 = 76
Furthermore, we can see that angle 2 equals angle 4 as they are vertically opposite angles
Thus, angle 2 = angle 4 = 76
Melissa drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours. When Melissa drove home, there was notraffic and the trip only took 5 hours. If her average rate was 21 miles per hour faster on the trip home, how far away does Melissa live from the mountains?Do not do any rounding.
Answers
Let
x ----> average rate on the trip home
y ----> average rate on the trip to the mountains
Remember that
The rate or speed is equal to dividing the distance by the time
speed=d/t
d=t*speed
on the trip home
d=5x -----> equation 1
on the trip to the mountains
d=8y ----> equation 2
we know that
her average rate was 21 miles per hour faster on the trip home
x=y+21 -----> equation 3
therefore
substitute equation 3 in equation 1
d=5(y+21) -----> equation 4
Equate equation 2 and equation 4 (because the distance is the same)
8y=5(y+21)
solve for y
8y=5y+105
8y-5y=105
3y=105
y=35
Find out the distance
d=8y
d=8(35)=280
The answer is 280 milesFind the exact values of the six trigonometric functions functions of the angles 0 shown in the figure. Sin, cos, tan, csc, sec and cot (Use the pythagorean theorem to find the third side of the triangle)

Answers
Answer:
\(undefined\)Explanation:
Let x represent the length of the third side of the given triangle.
We can go ahead and determine the value of x using the Pythagorean theorem as seen below;
\(\begin{gathered} 41^2=x^2+40^2 \\ 1681=x^2+1600 \\ x^2=1681-1600 \\ x^2=81 \\ x=\sqrt[]{81} \\ x=9 \end{gathered}\)So the length of the third side of the triangle is 9
We can now determine the value of sine theta as seen below;
\(\begin{gathered} \sin \theta=\frac{opposite\text{ side to angle }\theta\text{ }}{\text{hypotenuse}}=\frac{40}{41} \\ \therefore\sin \theta=\frac{40}{41} \end{gathered}\)We can see that sine theta is 40/41
Let's determine the value of cosine theta as seen below;
\(\begin{gathered} \cos \theta=\frac{\text{adjacent side to angle }\theta}{\text{hypotenuse}}=\frac{9}{41} \\ \therefore\cos \theta=\frac{9}{41} \end{gathered}\)So cosine theta is 9/41
Let's determine the value of tangent theta as seen below;
\(\begin{gathered} \tan \theta=\frac{opposite\text{ side to angle }\theta}{\text{adjacent side to angle }\theta}=\frac{40}{9} \\ \tan \theta=\frac{40}{9} \end{gathered}\)So tangent theta is 40/9
Let's now determine the value of cosecant theta as seen below;
\(\begin{gathered} \csc \theta=\frac{1}{\sin\theta}=\frac{1}{\frac{40}{41}}=1\div\frac{40}{41}=1\times\frac{41}{40}=\frac{41}{40} \\ \therefore\csc \theta=\frac{41}{40} \end{gathered}\)So the value of cosecant theta is 41/40
Let's determine the value of secant theta as seen below;
\(\begin{gathered} \sec \theta=\frac{1}{\cos\theta}=\frac{1}{\frac{9}{41}}=1\div\frac{9}{41}=1\times\frac{41}{9}=\frac{41}{9} \\ \therefore\sec \theta=\frac{41}{9} \end{gathered}\)So the value of secant theta is 41/9
Let's determine the value of cotangent theta as seen below;
\(\begin{gathered} \cot x=\frac{1}{\tan x}=\frac{1}{\frac{40}{9}}=1\div\frac{40}{9}=1\times\frac{9}{40}=\frac{9}{40} \\ \cot x=\frac{9}{40} \end{gathered}\)So the value of cotangent theta is 9/40
Vivian was assigned 12 math problems. Marco was assigned 3 times as many math problems as Vivian. Which equation could be used to find the total number of math problems Marco was assigned?
Answers
Answer:
12·3= Marco's math problems
Step-by-step explanation:
We know that Vivian was assigned 12.
We also know that Marco was assigned 3 times as many as Vivian, meaning we have to multiply:
12·3
=36
So, Marco was assigned 36 math problems.
Hope this helps! :)
can you simplify (9c^8)^1/2
Answers
Answer: 9c8
———
2
Step-by-step explanation:
32c8
Simplify 32c8———
2
I will mark you brainlist!

Answers
Explanation: you are trying to find the surface area. The formula for surface area is: Surface Area=2(width x length)+2(length x height)+2(height x width)
Since the question gives us the values of height, length and width. Just fill the information into the formula.
Surface Area=2(7x10)+2(10x3)+2(3x7)
Solve the parentheses:
Surface Area= 2(70)x2(30)+2(21)
Distribute the 2 into the parentheses:
Surface Area=140+60+42
Solve:
Surface Area=242
What is a number increased by 7 multiplied by 4?
Answers
Answer:
9?
Step-by-step explanation:
9 + 7 is `16, and 16 is a multiple of 4
How many and what type of solution(s) does the equation have?
6p^2 = 8p + 3
No real solutions
2 irrational solutions
1 rational solution
2 rational solutions
Answers
Answer:
2 irrational solutions.
Step-by-step explanation:
6p^2 = 8p + 3
0 = -6p^2 + 8p + 3
The roots are:
p = (2/3) - (8.5)^(1/2)/3, and
p = (2/3) + (8.5)^(1/2)/3
These are irrational numbers.
There are 2 irrational solutions.
Hey! Please help me ASAP

Answers
Answer:
-d+3.5≥4
Step-by-step explanation:
Just ask.
Hope this helps! :)
The lengths of a particular animal's pregnancies are approximately normally distributed, with mean μ=266 days and standard deviation σ=8 days. (a) What proportion of pregnancies lasts more than 278 days? (b) What proportion of pregnancies lasts between 256 and 270 days? (c) What is the probability that a randomly selected pregnancy lasts no more than 264 days? (d) A "very preterm" baby is one whose gestation period is less than 248 days. Are very preterm babies unusual?
Answers
A particular animal's pregnancy length is distributed normally with a mean μ = 266 days and a standard deviation σ = 8 days. We can calculate the probabilities of several events using this information.(a) The probability that pregnancy lasts more than 278 days is calculated as follows:
P(Z > (278-266)/8) = P(Z > 1.5) = 0.0668This implies that about 6.68 percent of pregnancies lasts more than 278 days.(b) The probability that pregnancy lasts between 256 and 270 days is calculated as follows:P(256 < X < 270) = P((256-266)/8 < Z < (270-266)/8) = P(-1.25 < Z < 0.5) = P(Z < 0.5) - P(Z < -1.25) = 0.6915 - 0.1056 = 0.5859.
This implies that about 58.59 percent of pregnancies lasts between 256 and 270 days.(c) The probability that a randomly selected pregnancy lasts no more than 264 days is calculated as follows:P(X ≤ 264) = P(Z ≤ (264-266)/8) = P(Z ≤ -0.25) = 0.4013This implies that about 40.13 percent of pregnancies last no more than 264 days.(d) A "very preterm" baby is one whose gestation period is less than 248 days.
The probability of a pregnancy being a "very preterm" baby is calculated as follows:P(X < 248) = P(Z < (248-266)/8) = P(Z < -2.25) = 0.0122This implies that only about 1.22 percent of pregnancies are "very preterm" babies. Therefore, very preterm babies are considered unusual.
is used to represent a variety of real-world situations, such as the distribution of people's heights or IQ scores. The most common method for calculating probabilities with a normal distribution is to use a table of values that has been precomputed to have the mean μ = 0 and standard deviation σ = 1.
The probabilities can be calculated by converting the random variable X to a standard normal variable Z. For X ~ N(μ, σ^2), Z = (X - μ)/σ ~ N(0, 1).The probabilities of several events related to a particular animal's pregnancy lengths, such as lasting more than 278 days or between 256 and 270 days, were calculated in the previous section using the normal distribution. These probabilities can be useful in answering questions such as how long a pregnancy is likely to last or whether a "very preterm" baby is unusual.
Therefore, we can conclude that a normal distribution can be used to model the pregnancy length of a particular animal, and probabilities can be calculated using the mean and standard deviation of the distribution. Based on the calculated probabilities, we can conclude that only about 6.68 percent of pregnancies lasts more than 278 days, about 58.59 percent of pregnancies lasts between 256 and 270 days, about 40.13 percent of pregnancies last no more than 264 days, and only about 1.22 percent of pregnancies are "very preterm" babies. Therefore, very preterm babies are considered unusual.
To know more about probability :
brainly.com/question/31828911
#SPJ11
Does this look good I made it this morning

Answers
Answer:
looks delicious
Step-by-step explanation:
Answer:
Man looks so good!
Step-by-step explanation:
Send me some in the mail. lol ☺☻♥
A nickel has a mass of 5 grams. What is the mass of the nickel in milligrams?
Answers
Answer:
5,000 milligrams
Step-by-step explanation:
Know That One 1 gram equals = 1,000 milligrams
Hope this Helps!
The coordinates of the vertices of AHKM are H(3, -2),
K(7, -5), and M(5. – 1). After a translation, the coordinates
of the vertices of the image of AHKM are H'(-3, 1). K'(1, -2),
and M'(-1, 2). What translation was performed on AHKM?
A (x, y) + (x+8, y-7)
B (x,y) =(x – 6, y + 3)
© (x, y) =(x+6, y - 3)
D (x,y) → (X-8y + 7)

Answers
Using translation concepts, the rule for the translation that was performed on AHKM is:
B. (x, y) =(x - 6, y + 3).
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction either in it’s definition or in it’s domain. Examples are shift left/right or bottom/up, vertical or horizontal stretching or compression, and reflections over the x-axis or the y-axis.
Looking at the vertices of the image compared to the original vertices, we have that:
For the x-coordinate, 6 was subtracted at every vertex.For the y-coordinate, 3 was added at every vertex.Hence the rule is given by:
B. (x, y) =(x - 6, y + 3).
More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
human blood is grouped into four types. the percentages of americans with each type are listed below. o 43% a 40% b 12% ab 5% choose one american at random. find the probability that this person a. has type b blood b. has type ab or o blood c. does not have type o blood
Answers
a. The probability of a randomly selected American having type B blood is 12%.
b. The probability of a randomly selected American having type AB or O blood is 48%.
c. The probability of a randomly selected American not having type O blood is 55%.
Human blood is categorized into four types which are A, B, AB, and O. The percentages of Americans who have each of the four types are given below:
O - 43% A - 40% B - 12% AB - 5%
To calculate probabilities for various scenarios, we can use these percentages as follows.
a. The probability of a randomly selected American having type B blood is 12%.
b. The probability of a randomly selected American having type AB or O blood is 48%. The combined percentage of O and AB blood types is 48%. We can therefore say that the probability of an American having O or AB blood is 48%.
c. The probability of a randomly selected American not having type O blood is 55%. The percentage of Americans who don't have type O blood is the sum of percentages of A, B, and AB blood types, which is Hence, the probability of not having O blood is lower than 57%. Therefore, the probability of a randomly selected American not having type O blood is 57%.
Learn more about Probability here:
brainly.com/question/13604758
#SPJ11
In finance, we need to do partial observations of data and estimate the data generating process (DGP) -- for example, log-normal returns. Sometimes, we can observe only the data points of a certain process, but we don't know what is the function generating the process. Consider the following graph is a plot of the f ′
(x), of a function f(x) given. What is the underlaying function ( f(x −
i)) that is the generator of the observed points in the plot f ′
(x −
i), for points x −
1=−1,x −
2=−0.9,…,x −
n=1?
Answers
The underlying function f(x - i) that generates the observed points f'(x - i) in the plot can be determined by integrating the observed points. By integrating f'(x - i), we can obtain f(x - i) up to a constant of integration.
The constant of integration can be determined by incorporating additional information or constraints related to the problem or by considering the behavior of the function at a specific point.
To find the underlying function f(x - i) that generates the observed points f'(x - i), we need to integrate the observed points.
Integration is the reverse process of differentiation, so by integrating f'(x - i), we can recover f(x - i) up to a constant of integration.
The constant of integration arises because integration does not provide a unique solution.
The constant represents an arbitrary additive term that can vary depending on the specific problem or additional constraints.
To determine the constant of integration, we may need additional information or consider specific conditions related to the problem.
It is also important to note that the accuracy of estimating the underlying function f(x - i) depends on the quality and quantity of the observed data points f'(x - i). More data points and precise measurements can lead to a better estimation of the underlying function.
Additionally, the behavior of the function at a specific point can provide valuable insights for determining the constant of integration and refining the estimation of the underlying function.
To learn more about integration visit:
brainly.com/question/31954835
#SPJ11
Yousef borrowed 1,690 last term for tuition, books, and student fees. This term he plans to borrow 2,345 because he knows his classes will be challenging and he doesn't want to work as much as last term. Estimate the amount of money Yousef will borrow by first rounding to the hundred
Answers
The estimate of the amount of money Yousef will borrow by first rounding to the hundred is 4000
Estimate the amount of money Yousef will borrow by first rounding to the hundredThe amount borrowed are given as:
Last term = 1690
This term = 2345
When the amounts are rounded to the nearest hundred, the amounts borrowed become:
Last term = 1700
This term = 2300
The total amount is then calculated as:
Total amount = Last term + This term
Substitute the known values in the above equation
Total amount = 1700 + 2300
Evaluate the sum
Total amount = 4000
Hence, the estimate of the amount of money Yousef will borrow by first rounding to the hundred is 4000
Read more about approximation at:
https://brainly.com/question/10171109
#SPJ1
Can someone help me with the equation below??

Answers
Answer:
The answer is number two o x< -2 or x > 5
Answer:
x<-2 or x>5 (the second choice)
Step-by-step explanation:
This is an "or" inequality. Both of the circles on the number line are open, so the signs we will use are going to be either < or >.
The shaded line on the left means x is less than -2 (x<-2). The shaded line on the right means x is greater than 5 (x>5).
If we write this as an "or" inequality, it will be...
x<-2 or x>5
In case you didn't know, if this was an "and" inequality, the shaded lines would intercept. But in this case, the shaded parts went opposite ways, so this is most likely an "or" inequality.
Hope this helped you out!! Have an amazing day c:
Minimize f(x)=2x2 1-2 x1 x 2+2x2-6 x 1 +6
Subject to: x1+x2-2=0
Using the Lagrange multipliers technique. Compute the optimal point values for x1, x2, l y ll
In an optimization problem with equality constraints, what is the meaning of the values of the Lagrange multipliers?
Answers
The optimal point values for x1, x2, λ, and μ (Lagrange multipliers) in the given problem are:
x1 = 1
x2 = 1
λ = -4
μ = 2
To solve the optimization problem using the Lagrange multipliers technique, we first construct the Lagrangian function L(x1, x2, λ) by incorporating the equality constraint:
L(x1, x2, λ) = f(x1, x2) - λ(g(x1, x2))
Where f(x1, x2) is the objective function, g(x1, x2) is the equality constraint, and λ is the Lagrange multiplier.
In this case, the objective function is f(x1, x2) = 2x1^2 - 2x1x2 + 2x2 - 6x1 + 6, and the equality constraint is g(x1, x2) = x1 + x2 - 2.
The Lagrangian function becomes:
L(x1, x2, λ) = 2x1^2 - 2x1x2 + 2x2 - 6x1 + 6 - λ(x1 + x2 - 2)
To find the optimal values, we need to find the critical points by taking partial derivatives of L with respect to x1, x2, and λ and setting them equal to zero. Solving these equations simultaneously, we get:
∂L/∂x1 = 4x1 - 2x2 - 6 - λ = 0
∂L/∂x2 = -2x1 + 2 + λ = 0
∂L/∂λ = -(x1 + x2 - 2) = 0
Solving these equations, we find x1 = 1, x2 = 1, and λ = -4. Substituting these values into the equality constraint, we can solve for μ:
x1 + x2 - 2 = 1 + 1 - 2 = 0
Therefore, μ = 2.
The optimal point values for the variables in the optimization problem are x1 = 1, x2 = 1, λ = -4, and μ = 2. The Lagrange multipliers λ and μ represent the rates of change of the objective function and the equality constraint, respectively, with respect to the variables. They provide insights into the sensitivity of the objective function to changes in the constraints and can indicate the impact of relaxing or tightening the constraints on the optimal solution. In this case, the Lagrange multiplier λ of -4 indicates that a small increase in the equality constraint (x1 + x2 - 2) would result in a decrease in the objective function value. The Lagrange multiplier μ of 2 indicates the shadow price or the marginal cost of satisfying the equality constraint.
To know more about optimal point values visit:
https://brainly.com/question/9429432
#SPJ11
Simplify: –3(y 2)2 – 5 6y What is the simplified product in standard form? y2 y.
Answers
Answer:
Simplify: –3(y + 2)2 – 5 + 6y
What is the simplified product in standard form?
-3
y2 +
-6
y +
-17
Step-by-step explanation:
The simplification of the given expression will be -17.
What is simplification?
The process of reducing the complex mathematical expressions into the simplest form is called simplification.
Given expression will be simplified as:-
= -3 ( y + 2 ) 2 - 5 + 6y
= ( -3y - 6 ) 2 - 5 + 6y
= ( -6y - 12 -5 + 6y )
= ( -17 )
Hence the simplification of the given expression will be -17.
To know more about Simplification follow
https://brainly.com/question/723406
#SPJ2
Geometry help please. Thank you!

Answers
what is the probability that a card drawn randomly from a standard deck of 52 cards is a black six? express your answer as a fraction in lowest terms.
Answers
The probability that a card drawn randomly from a standard deck of 52 cards is a black six is 1/26 in its lowest terms.
A probability is a numerical value that represents the possibility of an event occurring. It's a likelihood or chance of an event happening.
The formula for probability is:
P (A) = number of favorable outcomes/total number of outcomes
The probability of drawing a black six from a standard deck of 52 cards is 1/26. There are 52 cards in a standard deck, which are evenly divided into four suits of 13 cards each: hearts, diamonds, clubs, and spades. Each suit contains cards numbered 2 through 10, as well as four face cards: jack, queen, king, and ace. Only two of these cards, namely the six of clubs and the six of spades, are black sixes.
There are four suits in a standard deck, each with a six. As a result, there are 4 x 1 = 4 ways to select a six card. There are 52 cards in a deck, so the probability of drawing a black six is:
1/52 × 4= 1/13
There is only one black six in each suit, therefore there are two black sixes in a deck. Since there are 52 cards in a deck and two black sixes, the probability of drawing a black six is 2/52, which simplifies to 1/26 in its lowest terms.
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
An outboard motor on a boat has a cord to pull to start it. Advertisements boast that the motor "Starts on the first pull, every time!” In reality, the motor has a 95% chance of starting on each pull. A customer wants to know how many times he will have to pull the cord to start the motor.
Is it appropriate to use the geometric distribution to calculate probabilities in this situation?
Yes, the geometric distribution is appropriate.
No, since each trial is not independent of the other trials.
No, because it is not looking for the first occurrence of success.
No, since the probability of success is not the same for each of the trials.
Answers
Answer:
b i think.
Step-by-step explanation:
Answer: A. Yes the geometric distribution is appropriate
Step-by-step explanation:
got it right on edge
Can someone actually help me with these problems? They are due tomorrow.
43. Mr.Freeman has a square cornfield. Which of the following could be the area of the cornfield if the sides are measured in whole numbers? Select all that apply.
44. The area of each square in the figures below is 81 square units. Select the perimeter if each figure. Do any of the figures have the same perimeter? If so, explain why.
45. 13^3 =
46. 25^2=
47. 15^3 =
48. 34^2=
49. 5 × the square root of 121=
50. -6 × the square root of 36=
51. 10 × ^3 to the square root of 8=
52. -4 × the square root of 144=
53. 4r^3s =
These are the questions I need help with please help me asap with them
54. 9m^2n^4=

Answers
Answer:
Hope this helps you
Step-by-step explanation:
43. A "Square" cornfield, which means all 4 sides has the same lenght BxH
164.000 ft^2=404.96 NO
156.816 ft^2=396 Yes
174724 ft^2=418 Yes
215908 ft^2=464.66 NO
44. it's the same here, if the area is 81. then each side of the square is 9
1st figure: it has 12 sides x9 =108
2nd figure: it has 10 sides x9=90
3rd figure: has also 12 sides x9=108
45. 13^3= 13x13x13 = 2197
46. 25^2= 25x25 = 625
47. 15^3= 15x15x15 = 3375
48. 34^2= 34x34 = 1156
49. 5 root121= 5 (11)=55
50. -6.root36= - 6 (6)= -36
51. 10 root3 (8) = 10(2) = 20
52. -4. root 144= -4(12) = -48
The charge for renting a hedge trimmer is $10 plus $5 per day the total for renting a trimmer was $85. Which equation can you use to find the number of days the trimmer was rented? Please help !!!!
Answers
Answer:
15days.
Step-by-step explanation:
total amount=$85
renting amount=$10
amount per day=$5
to find the number of days the trimmer was rented it will be;
total amount-renting amount ÷$5
$85-$10÷$5
$75÷$5
=15days
Write the following permutation as a product of disjoint cycles and thereafter as a product of transpositions 1 2 3 4 5 6 7 8 8 2 6 3 7 4 5 1 (62848X)
Answers
The given permutation (62848X) can be expressed as the product of disjoint cycles as (1 6 2 8 4) and as the product of transpositions as (1 6)(6 2)(2 8)(8 4).
To express the given permutation (62848X) as a product of disjoint cycles, we start by examining each element and its corresponding image under the permutation.
1 maps to 6.
6 maps to 2.
2 maps to 8.
8 maps to 4.
4 maps to 8 (since X represents a fixed point, meaning it remains unchanged).
Now, let's write these mappings as disjoint cycles:
(1 6 2 8 4)
The cycle notation indicates that 1 maps to 6, 6 maps to 2, 2 maps to 8, 8 maps to 4, and 4 maps back to 1.
Next, we'll express this permutation as a product of transpositions. A transposition swaps two elements.
We can achieve this by breaking down the cycle (1 6 2 8 4) into transpositions:
(1 6)(6 2)(2 8)(8 4)
Each pair of adjacent elements within the cycle forms a transposition. For example, (1 6) represents the transposition that swaps 1 and 6, (6 2) swaps 6 and 2, and so on.
Thus, the given permutation (62848X) can be expressed as the product of disjoint cycles as (1 6 2 8 4) and as the product of transpositions as (1 6)(6 2)(2 8)(8 4).
To know more about permutation refer here:
https://brainly.com/question/32661405#
#SPJ11
Rita got three colors of beads, half of them are pink. She used all her pink beads to make some bracelets. If the number of pink beads she used for each bracelet is one eighths of the total number of beads, how many bracelets did she make?
Answers
Answer: she made 4 bracelets.
Step-by-step explanation:
Let x, y, z are the number of three kinds of beads, where x= number of pink beads.
As per given, number of pink beads= half of total beads
\(\Rightarrow\ x=\dfrac{1}{2}(x+y+z)\\\\\Rightarrow 2x= x+y+z\\\\\Rightarrow\ x= y+z\ \ \ ...(i)\)
Also, She used all pink beads, Number of pink beads she used for each bracelet= one eighths of the total number of beads
\(\dfrac{1}{8}(x+y+z)\\\\=\dfrac{1}{8}(x+x)\ \ \ [ {\text{From (i)}}]\)
\(=\dfrac{1}{8}(2x)\\\\=\dfrac{x}{4}\)bracelets =
Number of bracelets = (Number of pink beads) ÷ (Number of pink beads used for each bracelet)
\(=\dfrac{x}{\dfrac{x}{4}}=4\)
Hence, she made 4 bracelets.
Verify the identity.
2cos a * cos beta = cos(a + beta) + cos(a - beta)
Use the Sum and Difference Identities, and then simplify
cos(a + beta) + cos(alpha - beta) =cos alpha cos beta-sin a sin beta+ boxed | +sin alpha sin beta|
Answers
The given trigonometric identity \(\(2\cos(a) \cdot \cos(\beta) = \cos(a + \beta) + \cos(a - \beta)\)\) was verified using the sum and difference identities for cosine.
By simplifying the expressions and combining like terms, it was shown that both sides of the identity are equal.
To verify the identity \(\(2\cos(a) \cdot \cos(\beta) = \cos(a + \beta) + \cos(a - \beta)\),\) we will use the sum and difference identities for cosine and simplify the expression.
Using the sum identity for cosine, we have:
\(\(\cos(a + \beta) = \cos(a) \cdot \cos(\beta) - \sin(a) \cdot \sin(\beta)\)\)
Using the difference identity for cosine, we have:
\(\(\cos(a - \beta) = \cos(a) \cdot \cos(-\beta) - \sin(a) \cdot \sin(-\beta)\)\)
Since \(\(\cos(-\beta) = \cos(\beta)\) and \(\sin(-\beta) = -\sin(\beta)\),\) we can rewrite the difference identity as:
\(\(\cos(a - \beta) = \cos(a) \cdot \cos(\beta) + \sin(a) \cdot \sin(\beta)\)\)
Now we can substitute these expressions back into the original identity:
\(\(2\cos(a) \cdot \cos(\beta) = \cos(a + \beta) + \cos(a - \beta)\)\)
\(\(2\cos(a) \cdot \cos(\beta) = \cos(a) \cdot \cos(\beta) - \sin(a) \cdot \sin(\beta) + \cos(a) \cdot \cos(\beta) + \sin(a) \cdot \sin(\beta)\)\)
We can simplify the expression by combining like terms:
\(\(2\cos(a) \cdot \cos(\beta) = 2\cos(a) \cdot \cos(\beta)\)\)
The expression on the left-hand side is equal to the expression on the right-hand side, which confirms the identity:
\(\(2\cos(a) \cdot \cos(\beta) = \cos(a + \beta) + \cos(a - \beta)\)\)
Hence, the identity is verified.
To learn more about trigonometric identity click here: brainly.com/question/31837053
#SPJ11