Answers
Answer:
AC = 7.29 in
AB = 11.58 in
Step-by-step explanation:
tan 51 = 9/AC
1.2349 = 9/AC
AC = 7.29 in
sin 51 = 9/AB
0.7771 = 9/AB
AB = 11.58 in
Related Questions
You can afford a $1150 per month mortgage payment. You've found a 30 year loan at 8: interest compounded monthly. a) How big of a loan can you afford?
Answers
Answer:
PV= Max Loan amount = PMT*B(i,T) and PMT = 1200. Calculate B(i,T) = B(6%/12, 360)
=(12/.06)(1-(1/(1.005))360) I will let you complete the calculation
Step-by-step explanation:
Solve for x 15+5x=20x
Answers
Answer:
Step-by-step explanation:
15+5x=20x
-5x -5x => Subtract 5x from each side
You get
15 = 15x
Divide both sides by 15
1=x
Airplanes approaching the runway for landing are required to stay within the localizer (a certain distance left and right of the runway). When an airplane deviates from the localizer, it is sometimes referred to as an exceedence. Consider one airline at a small airport with six daily arrivals and an exceedence rate of 7%. a) Find the probability that on one day no planes have an exceedence. (2 points) b) Find the probability that at least 1 plane exceeds the localizer. (3 points) c) What is the expected number of planes to exceed the localizer on any given day? (2 points) d) What is the variance for the number of planes to exceed the localizer on any given day? (3 points)
Answers
Answer:
a) P(x = 0) = 64.69%
b) P(x ≥ 1) = 35.31%
c) E(x) = 0.42
d) var(x) = 0.3906
Step-by-step explanation:
The given problem can be solved using binomial distribution since:
There are n repeated trials independent of each other. There are only two possibilities: exceedence happens or exceedence doesn't happen.The probability of success does not change with trial to trial.The binomial distribution is given by
P(x) = ⁿCₓ pˣ (1 - p)ⁿ⁻ˣ
Where n is the number of trials, x is the variable of interest and p is the probability of success.
For the given scenario. the six daily arrivals are the number of trials
Number of trials = n = 6
The probability of success = 7% = 0.07
a) Find the probability that on one day no planes have an exceedence.
Here we have x = 0, n = 6 and p = 0.07
P(x = 0) = ⁶C₀(0.07⁰)(1 - 0.07)⁶⁻⁰
P(x = 0) = (1)(0.07⁰)(0.93)⁶
P(x = 0) = 0.6469
P(x = 0) = 64.69%
b) Find the probability that at least 1 plane exceeds the localizer.
The probability that at least 1 plane exceeds the localizer is given by
P(x ≥ 1) = 1 - P(x < 1)
But we know that P(x < 1) = P(x = 0) so,
P(x ≥ 1) = 1 - P(x = 0)
We have already calculated P(x = 0) in part (a)
P(x ≥ 1) = 1 - 0.6469
P(x ≥ 1) = 0.3531
P(x ≥ 1) = 35.31%
c) What is the expected number of planes to exceed the localizer on any given day?
The expected number of planes to exceed the localizer is given by
E(x) = n×p
Where n is the number of trials and p is the probability of success
E(x) = 6×0.07
E(x) = 0.42
Therefore, the expected number of planes to exceed the localizer on any given day is 0.42
d) What is the variance for the number of planes to exceed the localizer on any given day?
The variance for the number of planes to exceed the localizer is given by
var(x) = n×p×q
Where n is the number of trials and p is the probability of success and q is the probability of failure.
var(x) = 6×0.07×(1 - 0.07)
var(x) = 6×0.07×(0.93)
var(x) = 0.3906
Therefore, the variance for the number of planes to exceed the localizer on any given day is 0.3906.
A couple plans to purchase a house. The bank requires a 20% down payment on the $240,000 house. The couple will finance the rest of the cost with a fixed- rate mortgage at 8.5% annual interest with monthly payments over 30 years.
Complete the parts below. Do not round any intermediate computations. Round your final answers to the nearest cent if necessary. If necessary, refer to the list of financial formulas.
(a) Find the required down payment.
(b) Find the amount of the mortgage.
(c) Find the monthly payment.

Answers
(A) The required down payment is $48,000.
(B) The amount of the mortgage is $192,000.
(C) Monthly payment = $192,000 * (0.085/12) * (1 + (0.085/12))^(3012) / (((1 + (0.085/12))^(3012)) - 1)
(a) To find the required down payment, we need to calculate 20% of the house price.
Down payment = 20% of $240,000
Down payment = 0.2 * $240,000
Down payment = $48,000
The required down payment is $48,000.
(b) The amount of the mortgage is equal to the total cost of the house minus the down payment.
Mortgage amount = Total cost of the house - Down payment
Mortgage amount = $240,000 - $48,000
Mortgage amount = $192,000
The amount of the mortgage is $192,000.
(c) To find the monthly payment for the mortgage, we can use the formula for the monthly payment on a fixed-rate mortgage:
Monthly payment = P * r * (1 + r)^n / ((1 + r)^n - 1)
Where:
P = Principal amount (mortgage amount)
r = Monthly interest rate (8.5% annual interest divided by 12 months and converted to a decimal)
n = Total number of monthly payments (30 years multiplied by 12 months)
Monthly payment = $192,000 * (0.085/12) * (1 + (0.085/12))^(3012) / (((1 + (0.085/12))^(3012)) - 1)
Using this formula and performing the calculation will give you the monthly payment amount.
for more questions on down payment
https://brainly.com/question/1698287
#SPJ8
Find a . the mean ; b . the deviation from the mean for each data item ; and c . the sum of the deviations in part ( b ) for the following group of data items . 155 , 156 , 162 , 164 , 168
Answers
(a) The mean of the data item from the group data is 161.
(b) The deviation from the mean for each data is -6,-5,1,3 and 7. respectively.
(c) The sum of the deviation is 0
What is a group data?Grouped data are data formed by aggregating individual observations of a variable into groups, so that a frequency distribution of these groups serves as a convenient means of summarizing or analyzing the data.
(a) To find the mean of the data, we use the formula below.
Formula:
M = ∑x/n.......... Equation 1Where:
M = Mean = ?∑x = Sum of each data = 155+156+162+164+168 = 805n = Total number of data item = 5Substitute these values into equation 1
M = 805/5M = 161(b) To calculate the deviation from the mean (M') for each of the data item we use the formula below.
M' = x-M
For data 115,
M' = 155-161 = -6For data 156,
M' = -5For data 162,
M' = 162-161 = 1For data 164,
M' = 164-161M' = 3For data 168,
M' = 168-161M' = 7(c) The sum of the deviation is
∑M' = -6+(-5)+1+3+7∑M' = 0Hence, the mean, the diaviation from the mean is -6,-5,1,3 and 7 and the sum of the deviation of the data is 161 and 0 respectively,
Learn more about group data here: https://brainly.com/question/24298037
#SPJ1
Question is in the picture

Answers
Just 5*7 = 35
Then the answer is 4^35
Which number completes the
sequence? Type in your answer.
1, 2, 4, 7, 12, 19, 30, ?
Answers
The required next term at the end of the sequence is 43.
What is arithmetic progression?Arithmetic progression is the series of numbers that have common differences between adjacent values are equal.
here,
1, 2, 4, 7, 12, 19, 30,
As
the sequence is the prime addition of the number, as.
1,
1 + 1 = 2
2 + 2 = 4,
4 + 3 = 7
7 + 5 = 12
12 + 7 = 19
19 + 11 = 30
30 + 13 = 43
Thus, At the end of the sequence, the required next term is 43.
Learn more about arithmetic progression here: https://brainly.com/question/20334860
#SPJ1
PLEASE HELP ASAP!!!!!!

Answers
Applying the definition of complementary and supplementary angles, the measures are:
24. a. x = 23; b. m∠ECH = 28°; m∠HCD = 62°; d. m∠GCF = 28°; e. m∠ECG = 152°; f. m∠GCD = 118°
25. m∠F = 74°; 26. m∠1 = 41°; 27. x = 18; 28. m∠PQT = 94°
29. m∠H = 28°
30. m∠2 = 148°
What are Supplementary and Complementary Angles?Two angles that have a sum of 90 degrees are complementary, while two angles that have a sum of 180 degrees are supplementary.
24. a. m∠ECH + m∠HCD = 90° [complementary angles]
Substitute
x + 5 + 3x - 7 = 90
4x - 2 = 90
4x = 90 + 2
4x = 92
x = 23
b. m∠ECH = x + 5 = 23 + 5
m∠ECH = 28°
c. m∠HCD = 3x - 7 = 3(23) - 7
m∠HCD = 62°
d. m∠GCF = m∠ECH [vertical angles]
m∠GCF = 28°
e. m∠ECG = 180 - m∠GCF [supplementary angles]
m∠ECG = 180 - 28
m∠ECG = 152°
f. m∠GCD = 90 + m∠GCF
m∠GCD = 90 + 28
m∠GCD = 118°
25. m∠E + m∠F = 180 [supplementary angles]
Substitute
9x - 38 + 2x + 42 = 180
11x + 4 = 180
11x = 180 - 4
11x = 176
x = 16
m∠F = 2x + 42 = 2(16) + 42
m∠F = 74°
26. 6x + 11 = 10x - 9 [vertical angles]
6x - 10x = -11 - 9
-4x = -20
x = 5
m∠1 = 6x + 11 = 6(5) + 11
m∠1 = 41°
27. m∠ABC = 2(m∠DBC)
Substitute
9x - 4 = 2(79)
9x - 4 = 158
9x - 4 + 4 = 158 + 4
9x = 162
x = 18
28. m∠PQS = m∠SQR
Substitute
7x - 6 = 4x + 15
7x - 4x = 6 + 15
3x = 21
x = 7
m∠PQT = 180 - 2(m∠PQS)
m∠PQT = 180 - 2(7x - 6)
m∠PQT = 180 - 2(7(7) - 6)
m∠PQT = 94°
29. m∠G = 2(m∠H) + 6
m∠G + m∠H = 90 [complementary angles]
Substitute
2(m∠H) + 6 + m∠H = 90
3(m∠H) + 6 = 90
3(m∠H) = 90 - 6
3(m∠H) = 84
m∠H = 84/3
m∠H = 28°
30. m∠2 = 5(m∠1) - 12
m∠1 + m∠2 = 180 [linear pair]
Substitute
m∠1 + 5(m∠1) - 12 = 180
6(m∠1) - 12 = 180
6(m∠1) = 180 + 12
6(m∠1) = 192
m∠1 = 192/6
m∠1 = 32°
m∠2 = 5(m∠1) - 12 = 5(32) - 12
m∠2 = 148°
Learn more about complementary angles on:
https://brainly.com/question/16281260
#SPJ1
For each of the following subsets of R3 determine whether it is a vector subspace of R3 or not. Justify your answer.
Answers
So, b) and e) are subspaces of R3, and a), c), and d) are not.
a) {(x,y,z) ∈R3 : x = 0} is not a subspace of R3, because it doesn't contain the zero vector (0,0,0) which is a requirement for a subspace. It's also not closed under scalar multiplication.
b) {(x,y,z) ∈R3: x + y = 0} is a subspace of R3, because it's closed under scalar multiplication and addition and it contains the zero vector (0,0,0).
c) {(x,y,z) ∈R3 : xz = 0} is not a subspace of R3, because it's not closed under scalar multiplication and it's not closed under addition
d) {(x,y,z) ∈ R3: y ≥0} is not a subspace of R3, because it's not closed under addition, it doesn't contain the zero vector (0,0,0) and it's not closed under scalar multiplication.
e) {(x,y,z) ∈ R3: x = y = z} is a subspace of R3 because it satisfies all the properties of a subspace, it is closed under addition, scalar multiplication, it contains the zero vector (0,0,0) and the negative of any vector in the set is also in the set. This set contains all the vectors that are multiples of (1,1,1) which forms a subspace.
So, b) and e) are subspaces of R3, and a), c), and d) are not.
Complete Question: For each of the following subsets of R3 determine whether it is a vector subspace of R3 or not. Justify your answer.
a) {(x,y,z) ∈R3 : x = 0}
b) {(x,y,z) ∈R3: x + y = 0}
c) {(x,y,z) ∈R3 : xz = 0}
d) {(x,y,z) ∈ R3: y ≥0}
e) {(x,y,z) ∈ R3: x = y = z}
To learn more about Vector Subspaces
Visit; brainly.com/question/30031077
#SPJ4
find the area under the standard normal curve between z=0 and z=3
Answers
The area under the standard normal curve between z=0 and z=3 is 0.4987.
How to illustrate the information?It should be noted that because the normal distribution is symmetrical on both sides of the mean and is a continuous probability distribution, the right side of the center is the opposite of the left side.
The normal distribution was first termed by early statisticians who observed that the same shape repeatedly appeared in many distributions. The characteristics of normal distributions are as follows: Bell-like in its symmetry. The distribution's mean and median, which are both at its center, are equal.
The area will be illustrated as:
P(0 < Z < 3)
From the distribution table. In this case, it's important to look at the normal distribution table under the z score for the values of zero less than Z and Z less than 3. This will be:
= 0.9987 - 0.5
= 0.4987
Learn more about normal curves on:
https://brainly.com/question/27275125
#SPJ1
6thousandths times 8
Answers
Answer:
.048
Step-by-step explanation:
6 thousandths = 0.006
So, 0.006 times 8 would be...
.006
x 8
.048
Hope this helps you out! I'm not exactly sure how to explain how to multiply, but if you're confused, you can always ask someone for help...have a great day :)
A bottler of drinking water fills plastic bottles with a mean volume of 999 milliliters (ml) and standard deviation 7 ml. The fill
volumes are normally distributed. What is the probability that a bottle has a volume greater than 992 mL?
1.0000
0.8810
0.8413
0.9987
Answers
Answer:
0.8413
Step-by-step explanation:
Find the z score.
z = (x − μ) / σ
z = (992 − 999) / 7
z = -1
Use a chart or calculator to find the probability.
P(Z > -1)
= 1 − P(Z < -1)
= 1 − 0.1587
= 0.8413
The required probability that a bottle has a volume greater than 992 mL is 0.84134. Option C is correct
Given that,
A bottler of drinking water fills plastic bottles with a mean volume of 999 milliliters (ml) and a standard deviation of 7 ml. The fill volumes are normally distributed. What is the probability that a bottle has a volume greater than 992 mL, is to be determined
Probability can be defined as the ratio of favorable outcomes to the total number of events.
We use Z-statistic to find out the probability,
z = (x − μ) / σ
x = raw score = 992 mL
μ = population mean = 999 mL
σ = standard deviation
z = [992 − 999]/7
z = -1
P-value from Z-Table:
P(x<992) = 0.15866
P(x>992) = 1 - P(x<992) = 0.84134
Thus, the required probability that a bottle has a volume greater than 992 mL is 0.84134
Learn more about probability here:
brainly.com/question/14290572
#SPJ2
X is a normally distributed random variable with a mean of 22 and a standard deviation of 5. The probability that X is between 17 and 27 is Group of answer choices 0.6826 0.6931 0.3413 0.9931 0.0069
Answers
The probability that X is between 17 and 27 is given as follows:
0.6826.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation for this problem are given as follows:
\(\mu = 22, \sigma = 5\)
The probability that X is between 17 and 27 is the p-value of Z when X = 27 subtracted by the p-value of Z when X = 17, hence:
Z = (27 - 22)/5
Z = 1
Z = 1 has a p-value of 0.8413.
Z = (17 - 22)/5
Z = -1
Z = -1 has a p-value of 0.1587.
0.8413 - 0.1587 = 0.6826.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
7. When the height of the sand in a particular rectangular sandbox is
leveled out then the height of the sand, in inches (in.), is proportional to
the volume of sand, in cubic inches (in.3), in the sandbox. When the
height of the sand is 1.25 in. the volume of the sand is 280 in.3. A
playground has 3 of these sandboxes.
What is the total volume of the sand, in cubic inches (in.3), that is
needed for the playground when the height of the sand in each sandbox
is 4.5 in.?
Show your work in the provided space.
Answers
The Total volume of sand in cubic inches needed for the playground when the height of the sand in each sandbox is 4.5 in is; 2700 in³
How to solve mathematical proportions?
We are told that the height of the sand, in inches (in.), is proportional to
the volume of sand.
Let the volume be denoted as V
Let the height be denoted as h
Thus;
V ∝ h
Then to equate this, we will have a constant of proportionality;
V = kh
where k is constant of proportionality
When the height of the sand is 1.25 in., the volume of the sand is 280 in³ and this gives;
280 = 1.25k
k = 250/1.25
k = 200
Now, ware told that the height of sand in a box is now 4.5 inches and so;
V = 200 * 4.5
V = 900 in³
Since the playground has 3 of such boxes, then we can say that;
Total volume of sand on the playground = 900 * 3 = 2700 in³
Read more about Mathematical Proportions at; https://brainly.com/question/1781657
#SPJ1
The function f(x) = 1.85x2 models the cost of a square carpet, where x is the length in feet. Find the average rate of change for f, to the nearest tenth, over the interval 10 ≤ x ≤ 20.
Answers
To find the average rate of change of the function f(x) = 1.85x^2 over the interval 10 ≤ x ≤ 20, we need to find the difference in the function values at the endpoints of the interval and divide by the length of the interval.
The function value at x = 10 is:
f(10) = 1.85(10)^2 = 185
The function value at x = 20 is:
f(20) = 1.85(20)^2 = 740
The length of the interval is:
20 - 10 = 10
So the average rate of change of the function over the interval 10 ≤ x ≤ 20 is:
(f(20) - f(10)) / (20 - 10) = (740 - 185) / 10 = 55.5
Rounding to the nearest tenth, the average rate of change of the function over the interval 10 ≤ x ≤ 20 is approximately 55.5.
I need help with this

Answers
Answer:
y=(x-1)(x-6)
so x=1 or x=6
15 plants in 3 rows =
plants per row
HELPPPPP
Answers
Answer:
Step-by-step explanation:
45
Answer:
Step-by-step explanation:
5
William leaves his home at 15:03 and walks for 12 minutes to Euston station.
He spends 4 minutes buying a ticket and then catches the next train to Bletchley.
What time will he arrive at Bletchley?
Train timetable
Euston
14:49 15:18 15:29
14:52
15:32 15:35
Harrow
Watford 15:01
15:30
15:41 15:44 16:11
Hemel
15:39 15:50
15:53
16:20
Tring
15:31
16:00
Q
16:14 16:41
Bletchley 15:47
16:16
16:30
Bedford 15:54 16:23 16:34 16:37 17:04
15:32 15:59
Answers
To find out what time he will arrive at Bletchley, we need to look at the arrival time for the train that departs Euston at 15:32. According to the timetable, this train arrives at Bletchley at 16:16.
William spends 12 minutes walking to Euston station and 4 minutes buying a ticket, so his total journey time is 12 + 4 + 44 = 60 minutes (since there are 60 minutes in an hour). Therefore, he will arrive at Bletchley at 16:16 + 60 minutes = 17:16.
So, William will arrive at Bletchley at 17:16.
*Answer*
15:47
Step-by-step explanation:
He left; 15:03
Walk for; 12mins
Spends extra;4min
So by my side,
I'll sum up those values we're having to find the total time that was spent
12+4= 16mins
So, at that time when he reached at the station it was 15:19 when we add those extra mins
And so I think it'll 15:47
My thought told me so though
] Scientists trying to calculate the half-life (the time it takes for half of a sample to decay) of Phosphorus-32, took measurements of the sample once every day for five days. On what day should about a fourth of the original amount of P-32 remain? (Round answer to the nearest day.) Day Mass (g) 0 100 1 95 2 90.5 3 85 82 78 25 st 4 LO 5 ?
Answers
The time it will take for about a fourth of the original amount of P-32 remain is given as follows:
27 days.
How to define the exponential function?An exponential function is defined as follows:
y = ab^x.
In which:
a is the initial value.b is the rate of change.Considering that the initial amount is of 100, while after one day the amount was of 95, the parameters are given as follows:
a = 100, b = 95/100 = 0.95.
Hence the function for the amount remaining after x days is given as follows:
y = 100(0.95)^x.
One fourth of the amount will be remaining when y = 25, hence:
25 = 100(0.95)^x.
(0.95)^x = 0.25
xlog(0.95) = log(0.25)
x = log(0.25)/log(0.95)
x = 27 days.
More can be learned about exponential functions at https://brainly.com/question/30113628
#SPJ1
Identify the vertices of the feasible region and use them to find the maximum and/or minimum value for the given linear programming constraints.
System of Linear Programming:
z=−3x+5y
x+y≥−2
3x−y≤2
x−y≥−4
Maximum value of z:
Minimum value of z
Answers
The maximum value of the objective function is 26 and the minimum is -10
How to determine the maximum and the minimum values?The objective function is given as:
z=−3x+5y
The constraints are
x+y≥−2
3x−y≤2
x−y≥−4
Start by plotting the constraints on a graph (see attachment)
From the attached graph, the vertices of the feasible region are
(3, 7), (0, -2), (-3, 1)
Substitute these values in the objective function
So, we have
z= −3 * 3 + 5 * 7 = 26
z= −3 * 0 + 5 * -2 = -10
z= −3 * -3 + 5 * 1 =14
Using the above values, we have:
The maximum value of the objective function is 26 and the minimum is -10
Read more about linear programming at:
https://brainly.com/question/15417573
#SPJ1

write the equation representing the number of children in your family
Answers
Answer:
0+4
Step-by-step explanation:
1) Which number is composite?
5
9
11
2
Answers
5 and 11 are the only prime number here so I am not sure I am answering your question, sorry if this is not right or you can explain what it is asking so I can help you better.
Hope this helps :)
Find the difference. Write your answer in simplest form. 4 7/9 - 2 2/3
Answers
Answer:
\(= 2 \frac{1}{9} \\ \)
Step-by-step explanation:
\(4 \frac{7}{9} - 2 \frac{2}{3} \\ \frac{43}{9} - \frac{8}{3} \\ \frac{43 - 24}{9} \\ = \frac{19}{9} \\ = 2 \frac{1}{9} \)
hope this helps
brainliest appreciated
good luck! have a nice day!
A researcher wishes to test whether two nominal variables with two and three respective categories are statistically independent. She observes a chi square value from Pearson's chi square test of independence of 10.00430. Consider the following propositions: PROPOSITION ONE: At the 5% significance level the appropriate decision could be a Type II Error; PROPOSITION TWO: At the 1% significance level the appropriate decision could be a Type II Error.
A. Proposition I is true and Proposition II is true
B. Proposition I is true and Proposition II is false
C. Proposition I is false and Proposition II is true
D. Proposition I is false and Proposition II is false
E. None of the above
Answers
The correct answer is Option A: Proposition I is true and Proposition II is true.
A researcher can use Pearson's chi square test of independence to determine if two nominal variables are independent or not. In this case, the researcher observed a chi-square value of 10.00430.
To determine whether the null hypothesis should be accepted or rejected, the researcher must compare the chi-square value to a critical value associated with the desired level of significance.
At the 5% significance level, the critical value is usually around 7.815, and at the 1% significance level, the critical value is usually around 10.827. Since the observed chi-square value (10.00430) is higher than the critical values for both the 5% and 1% significance levels, the appropriate decision could be a Type II Error for both levels of significance.
In other words, Proposition I (At the 5% significance level the appropriate decision could be a Type II Error) and Proposition II (At the 1% significance level the appropriate decision could be a Type II Error) are both true.
For more questions like Chi-square test click the link below:
https://brainly.com/question/14082240
#SPJ4
What is the geometric mean of 12 and 9
Answers
Answer:
10.3923
Step-by-step explanation:
= ( 12 x 9 )^1/2
= ( 108 )^0.5
= 10.3923
Answer:
10.3923
Step-by-step explanation:
= ( 12 x 9 )0.5
= ( 108 )0.5
= 10.3923
Gail Ross met Jim Ryan (Problem 3) at Lane Bank. After talking with Jim, Gail decided she would like to consider the same loan on exact interest. Can you recalculate the loan for Gail under this assumption?
Answers
The loan for Gail under this assumption will be $14888.90.
How to calculate the loan?It should be noted that the maturity value is the addition of the simple interest and the principal. The time based on the complete information will be:
= (239 + 70)/365
= 0.075
The interest will be:
= 14000 × 0.075 × 309/365
= $888.90
Therefore, the maturity value will be:
= $14000 + $888.90
= $14888.90
Learn more about loan on:
brainly.com/question/26011426
#SPJ1
Quadrilateral ABCD is inscribed in this circle.
What is the measure of angle C?
Enter your answer in the box.

Answers
Answer:
m∠C = 122°
Step-by-step explanation:
Opposite angles of a quadrilateral inscribed in a circle are supplementary. This means
m∠A + m∠C = 180°
m∠B + m∠D = 180°
To find angle C we need to find x, then subtract m∠A from 180°
x+20=3x
20=2x
x=10
Now we substitute 10 in for x
m∠A=2(10)+38
m∠A=20+38
m∠A=58°
Now we subtract this value from 180.
m∠C=180-58
m∠C=122°
Answer:
62°
i took the test and this is the right answer
What is the volume of the triangular prism?
please help!! quickly its a test a look at the picture
7th grade math
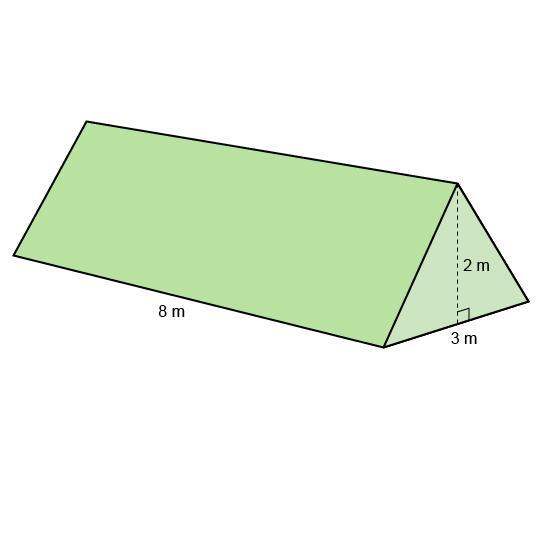
Answers
The area of the triangle is:
A = (base•height) : 2 = (3•2) : 2 = 3 m2
So the volume is:
V = 3 • 8 = 24 m3
2
5
9
10
Which statements are true? Select the two correct answers.
The square root of a positive number greater than 1 is less than the number.
The square root of a positive number is always less than half of the number itself.
The square root of a positive number less than 1 is less than the number.
The square root of a perfect square is not a whole number.
The square root of a positive number less than 1 is between 0 and 1.
TIME REM
38:-
Answers
Answer:
The square root of a positive number greater than 1 is less than the number The square root of a positive number is less than half of the number itselfKacie just bought a new house and needs to buy new sod for her backyard, if the dimensisons of her yard are 33.5 feet by 13.6 feet, what s the area if her yard
