Simplify your answer as much as possible
2(2v-7)=18
Answers
Answer:
v = 8
Step-by-step explanation:
Expand
4v - 14 = 18
Rearrange
4v = 18 + 14
4v = 32
v = 8
Answer:
2(2v-7)=18
4v-14=18
4v=32
v=8
Step-by-step explanation:
Related Questions
I NEED HELP WITH THESE WILL MARK BRAINLIST


Answers
Answer:
4-|8|+\(\sqrt[3]{8}\)
4-8 = -4 +\(\sqrt[3]{8}\) = -2
-2
Steve built a square hamster pen that has a perimeter of 240240240 centimeters.What is the length of one side of Steve's hamster pen
Answers
To find the length of one side of Steve's hamster pen, we can use the formula for the perimeter of a square, which is P = 4s, where P is the perimeter and s is the length of one side. In this case, we know that the perimeter is 240 centimeters, so we can set up the equation 240 = 4s. To solve for s, we can divide both sides by 4, which gives us s = 60 centimeters. Therefore, the length of one side of Steve's hamster pen is 60 centimeters. This means that all four sides of the pen are equal in length, and the area of the pen would be 60 x 60 = 3600 square centimeters.
Hi! To find the length of one side of Steve's square hamster pen with a perimeter of 240 centimeters, you can follow these steps:
1. Understand that the perimeter of a square is the sum of all its sides. In a square, all sides are equal.
2. Since there are 4 sides in a square, you can divide the total perimeter by 4 to find the length of one side.
3. Perform the calculation: 240 cm / 4 = 60 cm.
So, the length of one side of Steve's hamster pen is 60 centimeters.
To know more about perimeter visit:
https://brainly.com/question/397857
#SPJ11
The SC Electric Company has bid on two electrical wiring jobs. The owner of the company believes that
• the probability of being awarded the first job (Event A) is 0.75;
• the probability of being awarded the second job (Event B) is 0.5; and
• the probability of being awarded both jobs (A and B) is 0.375.
If the owner's beliefs are correct, which of the following statements must be true concerning event A and event B?
Answers
If the owner's beliefs are correct, the probability of being awarded the second job (Event B) is 0.5 . Event A and Event B are not mutually exclusive and are independent and must be true for event A and event B.
Simply put, the probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes.
By simply dividing the favorable number of possibilities by the entire number of possible outcomes, the probability of an occurrence can be determined using the probability formula. Because the favorable number of outcomes can never exceed the entire number of outcomes, the chance of an event occurring might range from 0 to 1. Additionally, the proportion of positive outcomes cannot be negative. In the sections that follow, let's go into greater detail on the fundamentals of probability.
Know more about probability at:
brainly.com/question/24756209
#SPJ4
Charge Q
1. =6.0nC is at (0.30 m,0), charge Q
2 =−1.0nC is at (0,0.10 m), and charge Q
3 =5.0nC is at (0,0). What is the magnitude of the net electrostatic force on the 5.0−nC charge due to the other charges? (k=8.99×10^9 N⋅m^2C ^2 )
Answers
The magnitude of the net electrostatic force on the 5.0−nC charge due to the other charges when the charge Q1 = 6.0 nC is at (0.30 m, 0), charge Q2 = −1.0 nC is at (0, 0.10 m), and charge Q3 = 5.0 nC is at (0, 0) is 6.21 N.
The value of the net electrostatic force on the 5.0-nC
charge due to the other charges when the charge Q1 = 6.0 nC is at (0.30 m, 0),
charge Q2 = −1.0 nC is at (0, 0.10 m), and
charge Q3 = 5.0 nC is at (0, 0) can be calculated as follows:
Given data,Charge Q1 = 6.0 nC is at (0.30 m, 0),
Charge Q2 = -1.0 nC is at (0, 0.10 m),
Charge Q3 = 5.0 nC is at (0, 0)
The formula to find out the force on the third charge Q3 is:
F = k * |Q1 * Q3| / r1^2 + k * |Q2 * Q3| / r2^2
Here, k = 8.99 × 10^9 N·m^2/C^2, Q1 = 6.0 nC, Q2 = -1.0 nC, Q3 = 5.0 nC
For the third charge Q3, the distance from Q1 is:
r1 = √(0.3^2 + 0^2) = 0.3 m
And the distance from Q2 is: r2 = √(0^2 + 0.1^2) = 0.1 m
Substituting all the given values in the formula:
F = 8.99 × 10^9 * [ (6.0 × 10^-9 * 5.0 × 10^-9) / 0.3^2 ] + 8.99 × 10^9 * [ (-1.0 × 10^-9 * 5.0 × 10^-9) / 0.1^2 ]F = 6.21 N
Therefore, the magnitude of the net electrostatic force on the 5.0−nC charge due to the other charges when the charge Q1 = 6.0 nC is at (0.30 m, 0), charge Q2 = −1.0 nC is at (0, 0.10 m), and charge Q3 = 5.0 nC is at (0, 0) is 6.21 N.
Learn more about net electrostatic force
brainly.com/question/30076646
#SPJ11
Evaluate if a=2, b=5, C=1
b(4a + c²)

Answers
Answer:
45
Step-by-step explanation:
5(4(2)+ 1²)
5(8 + 1²)
40 + 5
45
Solve for the formula m
e=mc squared
Answers
M = mass in grams, is this what you were looking for?
Step-by-step explanation:
Energy = mass in grams * speed of light measured in second^2
a diver makes 2.5 complete revolutions on the way from a 10.4 m high platform to the water. assuming zero initial vertical velocity, find the diver's average angular velocity during the dive.
Answers
The average angular velocity during the dive is 10.78 rad/sec.
Given,
displacement of the diver = 10.4m
as the diver falls freely then the acceleration will be g=9.8 \(m/s^2\)
To find average angular velocity during dive use formula,
\(\omega=\frac{\theta}{t}\)
where, θ=angular displacement and t= time taken to reach water
the diver makes 2.5 revolutions, here 1 revolution is 2π radians then total angular displacement is
θ=2.5* 2π=15.7 radian
To find time taken, use formula \(s=ut+\frac{1}{2}gt^2\)
here u=initial velocity=0
s=displacement of diver=10.4m
\(10.4=0+\frac{1}{2}9.8t^2\\\\10.4=4.9t^2\\\\2.122=t^2\\\\t=1.456 s\)
angular velocity, \(\omega=\frac{15.7}{1.456}=10.78\ rad/sec\)
Thus, the average angular velocity during the dive is 10.78 rad/sec.
To learn more about angular velocity refer here
https://brainly.com/question/14769426
#SPJ4
the angle bisector of angle acd in rhombus abcd makes a 64 degree angle with the diagonal bd. find the measure or angle bad
Answers
The measure of angle BAD in the rhombus ABCD can be determined as 116 degrees. The angle bisector of angle ACD forms a 64-degree angle with the diagonal BD.
To explain further, in a rhombus, the diagonals bisect each other at right angles. Let's consider the angle bisector of angle ACD. Since the angle bisector forms a 64-degree angle with the diagonal BD, the other half of the angle bisector (angle BAD) will also measure 64 degrees. Since angle BAD and angle BCD are adjacent angles that share the same vertex, the sum of their measures is 180 degrees. Therefore, angle BCD measures 180 - 64 = 116 degrees. Hence, the measure of angle BAD is 116 degrees.
Learn more about rhombus here: brainly.com/question/12665650
#SPJ11
Suppose that you are headed toward a plateau meters high. If the angle of elevation to the top of the plateau is ​, how far are you from the base of the​ plateau?
Answers
To determine the distance from the base of the plateau, knowing the height and the angle of elevation to the top, we can use trigonometry and the tangent function.
Let's assume the height of the plateau is 'h' meters and the angle of elevation to the top is 'θ'. We can set up a right triangle with the height of the plateau as the opposite side and the distance from the base to your position as the adjacent side. The tangent function relates the opposite and adjacent sides of a right triangle.
Using trigonometry, we can write the equation:
tan(θ) = h / distance
To isolate the distance, we rearrange the equation:
distance = h / tan(θ)
By plugging in the values for 'h' (height of the plateau) and 'θ' (angle of elevation), we can calculate the distance from the base to your position. Remember to ensure that the angle is in radians if the tangent function expects input in radians.
Keep in mind that this calculation assumes a flat ground leading up to the plateau and neglects any other obstacles or irregularities that might affect the actual distance.
Learn more about angle here:
https://brainly.com/question/13954458
#SPJ11
Jeremy has a loan from the bank. He owes $128,271. 60 including interest. He plans to pay the loan back in 18 years. How much must Elijah pay each month to have the loan paid in 18 years?
Answers
Answer:
593.85
Step-by-step explanation:
18*12 = 216 months
128271.60/216 = 593.85
B
20
29
C
21
1
Find sin(a) in the triangle.
A)20/21
B) 20/29
C) 21/20
D)21/29

Answers
Answer:
B) 20/29
Step-by-step explanation:
Sin(a) is equal to opposite side length divided by hypotenuse.
this is going to be my 13th reason please help me

Answers
Answer:
The radius of these cylinders is approximately 1 foot.
Step-by-step explanation:
According to this graph, the volume of the cylinder is directly proportional to its height, that is, radius remains constant. The expression of direct proportionality:
\(V \propto h\)
\(V = k\cdot h\) (1)
Where:
\(V\) - Volume of the cylinder, in cubic feet.
\(h\) - Height of the cylinder, in feet.
\(k\) - Proportionality constant, in square feet.
Besides, the proportionality constant is described by this expression:
\(k = \pi \cdot R^{2}\) (2)
Where \(R\) is the radius of the cylinder, in feet.
If we know that \(h = 9\,ft\) and \(V = 28.26\,ft^{2}\), then the radius of the cylinder is:
\(k = \frac{V}{h}\)
\(k = 3.14\)
\(R = \sqrt{\frac{k}{\pi} }\)
\(R \approx 1\,ft\)
The radius of these cylinders is approximately 1 foot.
Please help explanation if possible

Answers
Answer:
Step-by-step explanation:
The equation for the direct variation is, for us (using f and m instead of y and x):
f = km, where k is the constant of proportionality. We need to solve for this first using the first set of given values:
-19 = k(14) so
\(k=-\frac{19}{14}\) Now plug that in with second set of givens, namely to find f when m is 2:
\(f=(-\frac{19}{14})(2)\) and
\(f=-\frac{19}{7}\)
solve this question please: x² = -169
Answers
Answer:
13i, -13i
Step-by-step explanation:
To solve this equation, we need to take the square root of both sides. The square root of 169 can be either 13 or -13, but this time, they asked for -169. Whenever we take the square root of a negative number, we put the letter i, which stands for imaginary. It is never capitalized, so we remove the negative sign from -169, and take the square root of that. We get -13 and 13 as our answers, and we multiply both numbers by i to get -13i and 13i. Any solutions with i in it are considered complex solutions
find series solution for the following differential equation. your written work should be complete (do not skip steps).y'' 2xy' 2y=0
Answers
To find the series solution for the differential equation y'' + 2xy' + 2y = 0, we can assume a power series solution of the form:
Now, substitute y(x), y'(x), and y''(x) into the differential equation:
∑(n=0 to ∞) aₙn(n-1) xⁿ⁻² + 2x ∑(n=0 to ∞) aₙn xⁿ⁻¹ + 2 ∑(n=0 to ∞) aₙxⁿ = 0
We can simplify this equation by combining the terms with the same powers of x. Let's manipulate the equation step by step:
We can combine the three summations into a single summation:
∑(n=0 to ∞) (aₙ₊₂(n+1)n + 2aₙ₊₁ + 2aₙ) xⁿ = 0
Since this equation holds for all values of x, the coefficients of the terms must be zero. Therefore, we have:
This is the recurrence relation that determines the coefficients of the power series solution To find the series solution, we can start with initial conditions. Let's assume that y(0) = y₀ and y'(0) = y'₀. This gives us the following initial terms:
To know more about a series solution:- https://brainly.com/question/31522450
#SPJ11
which function has a range of {y|y ≤ 5}?
a. f(x) = (x – 4)2 5
b. f(x) = –(x – 4)2 5
c. f(x) = (x – 5)2 4
d. f(x) = –(x – 5)2 4
Answers
The correct option is \(\(b.\) \(f(x) = -\frac{{(x - 4)^2}}{5}\).\) The function that has a range of \(\(\{y | y \leq 5\}\)\) is option \(\(b.\) \(f(x) = -\frac{{(x - 4)^2}}{5}\).\)
To determine this, let's analyze the options:
\(\(a.\) \(f(x) = \frac{{(x - 4)^2}}{5}\)\): This function will have a range of \(\(y\)\)-values greater
than or equal to 0, so it does not have a range of \(\(\{y | y \leq 5\}\).\)
\(\(b.\) \(f(x) = -\frac{{(x - 4)^2}}{5}\)\) : This function is a downward-opening parabola, and when we substitute various values of \(\(x\)\) , we get \(\(y\)\)-values less than or equal to 5. Therefore, this function has a range of \(\(\{y | y \leq 5\}\).\)
\(\(c.\) \(f(x) = \frac{{(x - 5)^2}}{4}\)\): This function is an upward-opening parabola, and its
range will be \(\(y\)\)-values greater than or equal to 0, so it does not have a
range of \(\(\{y | y \leq 5\}\).\)
\(\(d.\) \(f(x) = -\frac{{(x - 5)^2}}{4}\)\): This function is a downward-opening parabola, and its range will be \(\(y\)\)-values less than or equal to 0, so it
does not have a range of \(\(\{y | y \leq 5\}\).\)
Therefore, the correct option is \(\(b. f(x) = -\frac{{(x - 4)^2}}{5}\).\)
To know more about parabola visit-
brainly.com/question/31047093
#SPJ11
simply the picture above..
write your answer using only positive exponents..:/

Answers
Answer:
27/64m^12 n^6
Step-by-step explanation:
another advantage of using anova is that it ________ so the significant differences can be located and interpreted easily.
Answers
Another advantage of using Anova is that it arranges the means so the significant differences can be located and interpreted easily.
The ANOVA test is a type of statistical test used to determine whether there is a statistically significant difference between two or more categorical groups by testing mean differences using variance.
Another important part of the ANOVA is the splitting of the independent variables into two or more groups.
The assumptions for the ANOVA test are the same as those for general parametric tests.
ANOVA can only be performed if there is no relationship between subjects in each sample. Sample size for different groups/levels must be the same.ANOVA can only be performed if the dependent variable is normally distributed.the population variances of must be equal (that is, homoscedasticity). Homogeneity of variance means that the variability of results is similar across populations.Advantages of ANOVA:
The z-test can only be used to compare two population means, whereas the ANOVA test can be used to compare three or more population means.When there are two different treatments/factors affecting the dependent variable, the Two Way ANOVA test can be used to analyze the effect of each treatment.To learn more about ANOVA test , refer:
https://brainly.com/question/15084465
#SPJ4
What is 75% of 200? Select one: O 50 O C 125 O 150 O 15
Answers
Answer:
75% of 200 is 150 ! :) .......
Answer:
C: 150 :)
75% of 200 is 150
Help with my mathhhhh
Answers
Answer:
See the image below for the answer:)
Step-by-step explanation:

A painting hangs in a museum with the bottom of the painting 1 metre above the eye level. The painting is 2 metres tall and the angle of view is 30 degrees. How far away from the wall is the viewer
Answers
The viewer is standing approximately 1.732 meters away from the wall.
Let's assume that the viewer is standing at a distance x from the wall, and let h be the height of the painting above the viewer's eye level. Then we can use trigonometry to relate these quantities.
First, we can find the actual height of the painting as it appears to the viewer:
Actual height = (Height of painting) / cos(angle of view)
= 2 / cos(30 degrees)
= 2 / sqrt(3)
Next, we can find the angle between the viewer's line of sight and the top edge of the painting. This is an angle in a right triangle with adjacent side x and opposite side h, so we have:
tan(angle) = h / x
Solving for h, we get:
h = x * tan(angle)
In this case, the angle is 30 degrees, and h is given as 1 meter (the height of the bottom of the painting above the viewer's eye level). So we have:
1 = x * tan(30 degrees)
x = 1 / tan(30 degrees)
x = 1.732 meters
Therefore, the viewer is standing approximately 1.732 meters away from the wall.
Learn more about angle here:
https://brainly.com/question/30147425
#SPJ11
List all possible rational zeros given by the Rational Zeros Theorem (but don't check to see which actually are zeros). (Enter your answers as a comma-separated list.)Q(x) = x^4 − 4x^3 − 9x + 10x =
Answers
The possible zeros of x are 1,-1,2,-2,5,-5,10,-10 when the function is Q(x)= x⁴-4x³-9x+10 from the rational zeros theorem.
Given that,
We have to list every rational zero that can be derived from the Rational Zeros Theorem, without determining which ones are actually zero. (Separate your responses into a list using commas.)
The function is Q(x)= x⁴-4x³-9x+10
The x value is what we have to find.
We know that,
According to rational zeros theorem,
The possible zeros are
x= factor of 10/ factor of 1
x= ±1,±2,±5,±10/±1
x=1,-1,2,-2,5,-5,10,-10
Therefore, The possible zeros of x are 1,-1,2,-2,5,-5,10,-10 when the function is Q(x)= x⁴-4x³-9x+10 from the rational zeros theorem.
To learn more about zeros visit: https://brainly.com/question/27551059
#SPJ4
What is the variable expression that represents the word phrase.
The product of 2 and x is increased by 7
Answers
Answer:
2x + 7
Step-by-step explanation:
The product of 2 and x
Product means multiplication
The product of 2 and x means multiplication of 2 and x
Which is equivalent to
2 * x = 2x
The product of 2 and x is increased by 7
That is, 7 is added to the product of 2 and x
Here,
2x + 7
The variable expression that represent the word phrase "The product of 2 and x is increased by 7" is 2x + 7
Orders for cakes are taken by one baker in a bakery. The time to bake a cake and decorate it is exponentially distributed, with a mean of 2.5 hours. The baker completes one cake before beginning the next. Orders for cakes arrive at a mean rate of two cakes per day and are Poisson distributed. Assuming the baker works eight hour workdays, determine:
Answers
a) On average, there are approximately 0.246 cakes waiting to be baked.
b) On average, a cake spends approximately 0.369 hours (or 22 minutes) waiting to be baked.
c) The average time a cake spends being decorated is 2.5 hours.
d) On average, it takes approximately 2.869 hours (or 2 hours and 52 minutes) from the arrival of an order to the completion of the cake.
To determine the following parameters, we need to use the concepts of exponential distribution, Poisson distribution, and basic queuing theory. Here are the calculations for each parameter:
(a) The average number of cakes waiting to be baked:
The average number of cakes waiting to be baked can be calculated using the queuing theory formula for an M/M/1 queuing system (where arrivals follow a Poisson process, service times follow an exponential distribution, and there is one server). The formula is given by:
Lq = (λ^2) / (μ * (μ - λ))
Given:
λ = 2 cakes per day (mean arrival rate)
μ = 1 / 2.5 cakes per hour (mean service rate)
First, we need to convert the arrival rate to the same time unit as the service rate (hours). Since there are 8 hours in a workday, we have:
λ = 2 cakes per day * (1 day / 24 hours) * (8 hours / 1 workday) = 2 / 3 cakes per hour
Substituting the values into the formula:
Lq = ((2/3)^2) / (1 / 2.5 * (1 / 2.5 - 2/3))
Lq ≈ 0.246 cakes
Therefore, on average, there are approximately 0.246 cakes waiting to be baked.
(b) The average time a cake spends waiting to be baked:
The average time a cake spends waiting to be baked can be calculated using Little's Law, which states that the average number of customers in a system is equal to the arrival rate multiplied by the average time spent in the system. In this case, the system is the baker's work process.
Using Little's Law:
Lq = λ * Wq
We already know Lq = 0.246 cakes (from the previous calculation), and λ = 2/3 cakes per hour (as calculated before).
Substituting the values into the formula:
0.246 = (2/3) * Wq
Wq = 0.369 hours
Therefore, on average, a cake spends approximately 0.369 hours (or 22 minutes) waiting to be baked.
(c) The average time a cake spends being decorated:
Since the baker completes one cake before beginning the next, the time spent decorating a cake is equal to the service time, which follows an exponential distribution. The mean service time is given as 2.5 hours.
Therefore, the average time a cake spends being decorated is 2.5 hours.
(d) The average time from the arrival of an order to the completion of the cake:
The average time from the arrival of an order to the completion of the cake is the sum of the average time spent waiting to be baked and the average time spent being decorated.
Average time = Average time waiting + Average time being decorated
Average time = 0.369 hours + 2.5 hours
Average time ≈ 2.869 hours
Therefore, on average, it takes approximately 2.869 hours (or 2 hours and 52 minutes) from the arrival of an order to the completion of the cake.
Learn more about average here:
https://brainly.com/question/29550341
#SPJ11
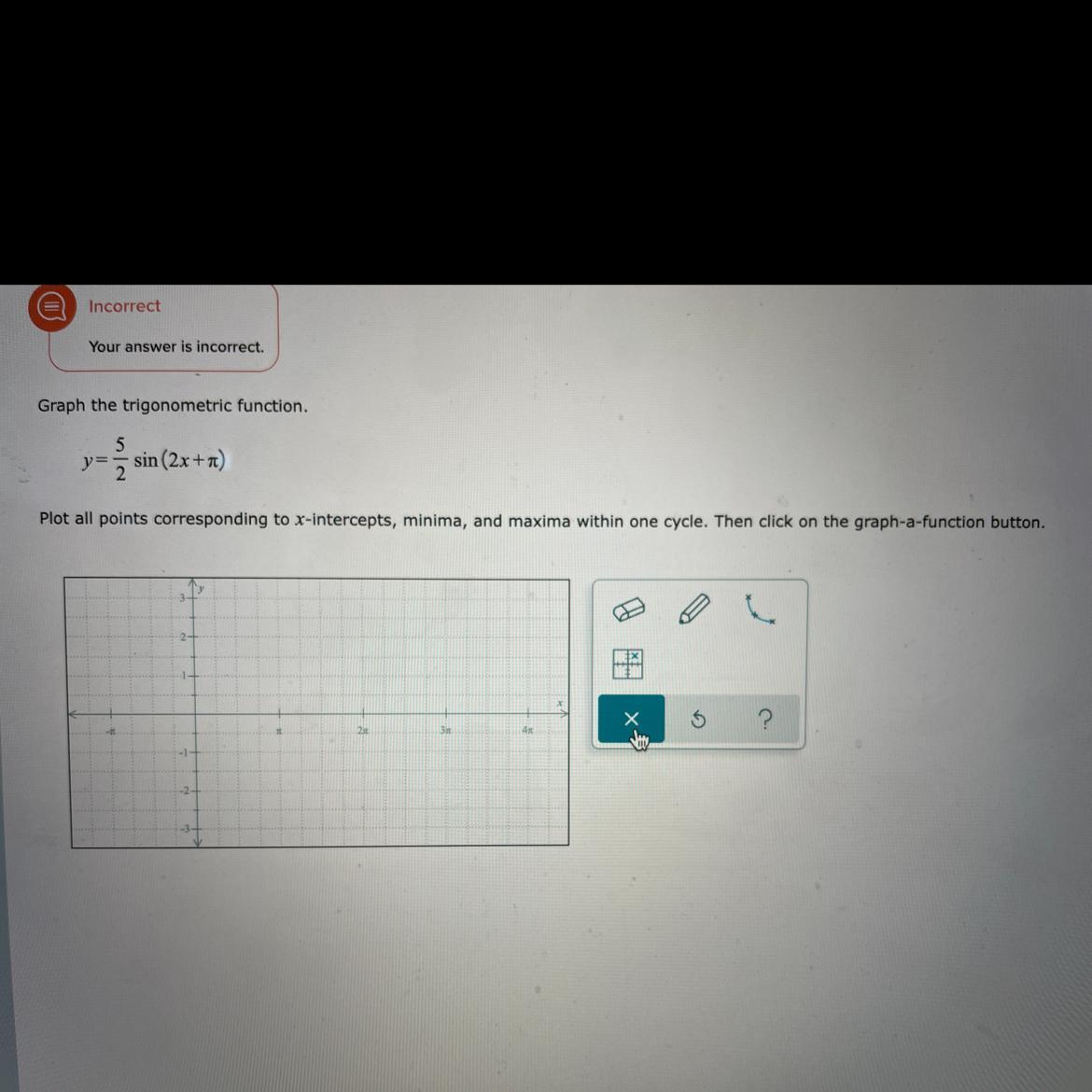
Please help me. I’m not so familiar with graphing.
Answers
Answer:
Hey i believe this is the answer
Step-by-step explanation:
Take a look at the screenshot
Also Desmos graphing calculator is a big help :) It might make you a little more confident

PLEASE HELP AND EXPLAIN HOW YOU GOT THE ANSWER. I WILL MARK YOU BRAINLIEST

Answers
Answer:
its A
Step-by-step explanation:
DeAndre downloaded 8 apps onto his tablet in 12 seconds. At this rate, how many apps could he download in one minute? (12 seconds = 15 minute)
HELP
Answers
Explanation:
60 divided by 12 is 5. That’s how many downloading sessions could fit in a minute. Multiply 5 by the number of apps, which is 8. Your answer is 40 apps.
How do you compare exponential functions??
I really don't understand, also giving brainliest!!
Answers
Answer:
You compare it by this
Step-by-step explanation:
Linear functions are graphed as straight lines while exponential functions are curved. Linear functions are typically in the form y = mx + b, which is used to discover the slope, or simply the change in y divided by the change in x, while exponential functions are typically in the form y = (1 + r) x.
(i) Let V=2xy^2z ^3+3ln(x ^2+2y ^2+3z^2)N in free space. Guduate each of the following amounts in P(3,2,−1) (a) V (b) ∣V∣ (c) E (d) ∣E∣
Answers
The electric potential, V, is 73.63 N and the magnitude of the electric field is 12.00 V/m.
The given electric potential is,V=2xy²z³+3ln(x²+2y²+3z²) N
The components of the electric field can be found as follows,
E=-∇V=- (∂V/∂x) i - (∂V/∂y) j - (∂V/∂z) k
(a) To determine the potential at P(3, 2, -1), substitute x=3, y=2, and z=-1 in the given potential,
V=2(3)(2²)(-1)³ + 3 ln [(3)²+2(2)²+3(-1)²]= 72.32 N
(b) The magnitude of the potential is given by,
|V|= √ (Vx²+Vy²+Vz²)
The electric potential, V, is a scalar quantity. Its magnitude is always positive. Therefore,
|V|= √ [(2xy²z³)² + (3ln(x²+2y²+3z²))²]= √ [(-72)² + (16.32)²]= 73.63 N
(c) To determine the electric field E at P(3,2,-1), find the partial derivatives of V with respect to x, y, and z, and then substitute x=3, y=2, and z=-1 to obtain Ex, Ey, and Ez.
Ex = -(∂V/∂x)= -2y²z³/(x²+2y²+3z²) = -4.8 V/m
Ey = -(∂V/∂y)= -4xyz³/(x²+2y²+3z²) = -10.67 V/m
Ez = -(∂V/∂z)= -6xyz²/(x²+2y²+3z²) = 5.33 V/m
Therefore, the electric field E at P(3,2,-1) is, E=Exi+Eyj+Ezk=-4.8 i - 10.67 j + 5.33 k
(d) The magnitude of the electric field is given by,
|E|= √ (Ex²+Ey²+Ez²)= √ [(4.8)²+(10.67)²+(5.33)²]= 12.00 V/m
To know more about electric potential, visit:
https://brainly.com/question/28444459
#SPJ11
I need help on 16 17 and 18

Answers
Answer:
Step-by-step explanation:
16. 6.9, or 69/10
17. D, 12 feet
18. 6 11/12