Simplify. 11 3/4-8 1/2
Answers
Therefore, 11 3/4 - 8 1/2 = 13/4, or 3 1/4 as a mixed number.
What is mixed number?A mixed number is a type of number that represents a whole number and a fraction together. It is written in the form of a whole number followed by a fraction, such as 3 1/2. The whole number represents the number of whole units, while the fraction represents the part of a unit.
For example, the mixed number 3 1/2 can be interpreted as three whole units and one half of a unit. Another example of a mixed number is 2 3/4, which represents two whole units and three-quarters of a unit. Mixed numbers are commonly used in everyday life, such as in cooking and measuring, and in mathematical calculations involving fractions.
To subtract mixed numbers like these, we need to convert them to improper fractions first:
\(11 3/4 = (4 * 11 + 3)/4 = 47/4\)
\(8 1/2 = (2 * 8 + 1)/2 = 17/2\)
Now, we can subtract the fractions:
\(47/4 - 17/2\)
To subtract these fractions, we need to find a common denominator. The least common multiple of 4 and 2 is 4 × 2 = 8. We can convert both fractions to have a denominator of 8:
\(47/4 = (47/4) * (2/2) = 94/8\)
\(17/2 = (17/2) * (4/4) = 68/8\)
Now, we can subtract the numerators:
\(94/8 - 68/8 = 26/8\)
Finally, we can simplify the result by dividing both numerator and denominator by their greatest common factor, which is 2:
\(26/8 = (2 * 13)/(2 * 4) = 13/4\)
To know more about common factor, visit:
https://brainly.com/question/30961988
#SPJ1
Related Questions
Keith who runs a daycare center bought 14 gallons of paint to do up the classroom how many classrooms can he get painted in all if each room requires 7/4 gallons of paint
Answers
Answer:
Keith bought 14 gallons of paint, and each classroom requires 7/4 gallons of paint.
To find how many classrooms can be painted, we can divide the total amount of paint by the amount of paint needed per classroom:
14 ÷ (7/4) = 8
Therefore, Keith can paint 8 classrooms in total.
How would I do this?

Answers
Answer:
we cant see the full picture :(
flaws in a certain type of drapery material appear on the average of two in 150 square feet. if we assume a poisson distribution, find the probability of at most 2 flaws in 450 square feet.
Answers
Assuming a poisson distribution, the probability of having at most 2 flaws in 450 square feet is approximately 0.062 or 6.2%.
For the probability of at most 2 flaws in 450 square feet, we can use the Poisson distribution.
The Poisson distribution is commonly used to model the number of events occurring in a fixed interval of time or space when the events occur with a known average rate and independently of the time since the last event.
In this case, we are given that the average number of flaws in 150 square feet is two. Let's denote this average as λ (lambda).
We can calculate λ using the given information:
λ = average number of flaws in 150 square feet = 2
Now, let's find the probability of at most 2 flaws in 450 square feet. Since the area of interest is three times larger (450 square feet), we need to adjust the average accordingly:
Adjusted λ = average number of flaws in 450 square feet = λ * 3 = 2 * 3 = 6
Now we can use the Poisson distribution formula to find the probability. The formula is as follows:
P(X ≤ k) = e^(-λ) * (λ^0 / 0!) + e^(-λ) * (λ^1 / 1!) + e^(-λ) * (λ^2 / 2!) + ... + e^(-λ) * (λ^k / k!)
In this case, we need to calculate P(X ≤ 2), where X represents the number of flaws in 450 square feet and k = 2. Plugging in the values, we get:
P(X ≤ 2) = e^(-6) * (6^0 / 0!) + e^(-6) * (6^1 / 1!) + e^(-6) * (6^2 / 2!)
Calculating each term:
P(X ≤ 2) = e^(-6) * (1 / 1) + e^(-6) * (6 / 1) + e^(-6) * (36 / 2)
Now, let's calculate the exponential term:
e^(-6) ≈ 0.00248 (rounded to five decimal places)
Substituting this value into the equation:
P(X ≤ 2) ≈ 0.00248 * 1 + 0.00248 * 6 + 0.00248 * 18
Calculating each term:
P(X ≤ 2) ≈ 0.00248 + 0.01488 + 0.04464
Adding the terms together:
P(X ≤ 2) ≈ 0.062 (rounded to three decimal places)
Therefore, the probability of having at most 2 flaws in 450 square feet is approximately 0.062 or 6.2%.
To know more about Poisson distribution refer here:
https://brainly.com/question/30388228#
#SPJ11
1. A dog food company is interested in how much dog food a dog consumes based off of its weight. The company takes a random sample of dogs and finds that the best regression model to represent the data is as follows:Simple Linear Regression Results:Dependent Variable: Ounces of Food Consumed in a WeekIndependent Variable: WeightFood Consumed=−32.86+5.25×WeightSample Size: 500R2: 0.8129Estimate of error standard deviation: 7.8563121Suppose that a dog weighs 42.4 pounds, and typically eats 180 ounces of food per week. How many ounces of food would we predict the dog eats in a week, based on the least squares estimate? Provide your answer accurate to 1 digit past the decimal point.2. Suppose another dog weighs 24.7 pounds and consumes 70 ounces of food per week. What is the residual associate to this individual using the least squares estimate? Provide your answer accurate to 1 digit past the decimal point.
Answers
The residual associated with this individual is approximately -15.4 ounces, using the least squares estimate. This means that the actual amount of food consumed is about 15.4
We would predict that the dog would eat approximately 180.96 ounces of food in a week, based on the least squares estimate. the residual associated with this individual is approximately -15.4 ounces, using the least squares estimate. This means that the actual amount of food consumed is about 15.4 ounces less than what would be predicted based on the regression model.
Using the given regression model, we can estimate the amount of food a dog weighing 42.4 pounds would consume in a week as:
Food Consumed = -32.86 + 5.25 × Weight
Food Consumed = -32.86 + 5.25 × 42.4
Food Consumed ≈ 180.96 ounces
Therefore, we would predict that the dog would eat approximately 180.96 ounces of food in a week, based on the least squares estimate.
To find the residual associated with a dog weighing 24.7 pounds and consuming 70 ounces of food per week, we first need to calculate the predicted value of food consumed based on the given regression model:
Food Consumed = -32.86 + 5.25 × Weight
Food Consumed = -32.86 + 5.25 × 24.7
Food Consumed ≈ 85.38 ounces
The residual is then calculated as the difference between the actual value of food consumed (70 ounces) and the predicted value (85.38 ounces):
Residual = Actual Value - Predicted Value
Residual = 70 - 85.38
Residual ≈ -15.4 ounces
Therefore, the residual associated with this individual is approximately -15.4 ounces, using the least squares estimate. This means that the actual amount of food consumed is about 15.4 ounces less than what would be predicted based on the regression model.
Learn more about regression model
https://brainly.com/question/14983410
#SPJ4
Find the length and width of the greatest rectangular area that the farmer can enclose with 100 m of fencing. the length is m and the width is m.
Answers
Answer:
25 length and 25width
Step-by-step explanation:
we need to find the biggest area with a perimeter of 100 and all sides need to be the same. So you divide 100 by 4 and you get 25 for width and 25 for length
How do I solve this problem

Answers
Answer:
Step-by-step explanation:
In this math, we will be using the law of cosine.
a2 = b2 + c2 − 2bc cosA
This is to note that a here is actually x
a= x
b = 10
c = 9.4
cosA = cos20°
\(a = \sqrt{b^{2} +c^{2} - (2bc*cosA) }\\\\a= \sqrt{100 +88.36 - (188- 0.94)} \\\\a = \sqrt{1.3}\\\\a = 1.14\)
a multiple-choice test contains 7 questions. there are four possible answers for each question. in how many ways can a student answer the questions on the test if the student answers every question?
Answers
student can answer the questions on the test in 16,384 different ways if they answer every question.
To determine the number of ways a student can answer the questions on a multiple-choice test containing 7 questions with four possible answers for each question, we will use the multiplication principle. The multiplication principle states that if there are a number of independent choices, then the total number of possible outcomes is the product of the number of choices.
Identify the number of questions and possible answers. In this case, there are 7 questions and 4 possible answers for each question.
Calculate the number of ways to answer each question. Since there are 4 possible answers for each question, there are 4 ways to answer each of the 7 questions.
Apply the multiplication principle. To find the total number of ways to answer all 7 questions, multiply the number of ways to answer each question:
Total number of ways = (4 ways for question 1) x (4 ways for question 2) x ... x (4 ways for question 7)
Perform the calculation. Since there are 7 questions and 4 ways to answer each question, the total number of ways is:
Total number of ways = 4^7 = 16,384
for more questions on multiplication principle
https://brainly.com/question/2063455
#SPJ11
Anyone know how to do this?
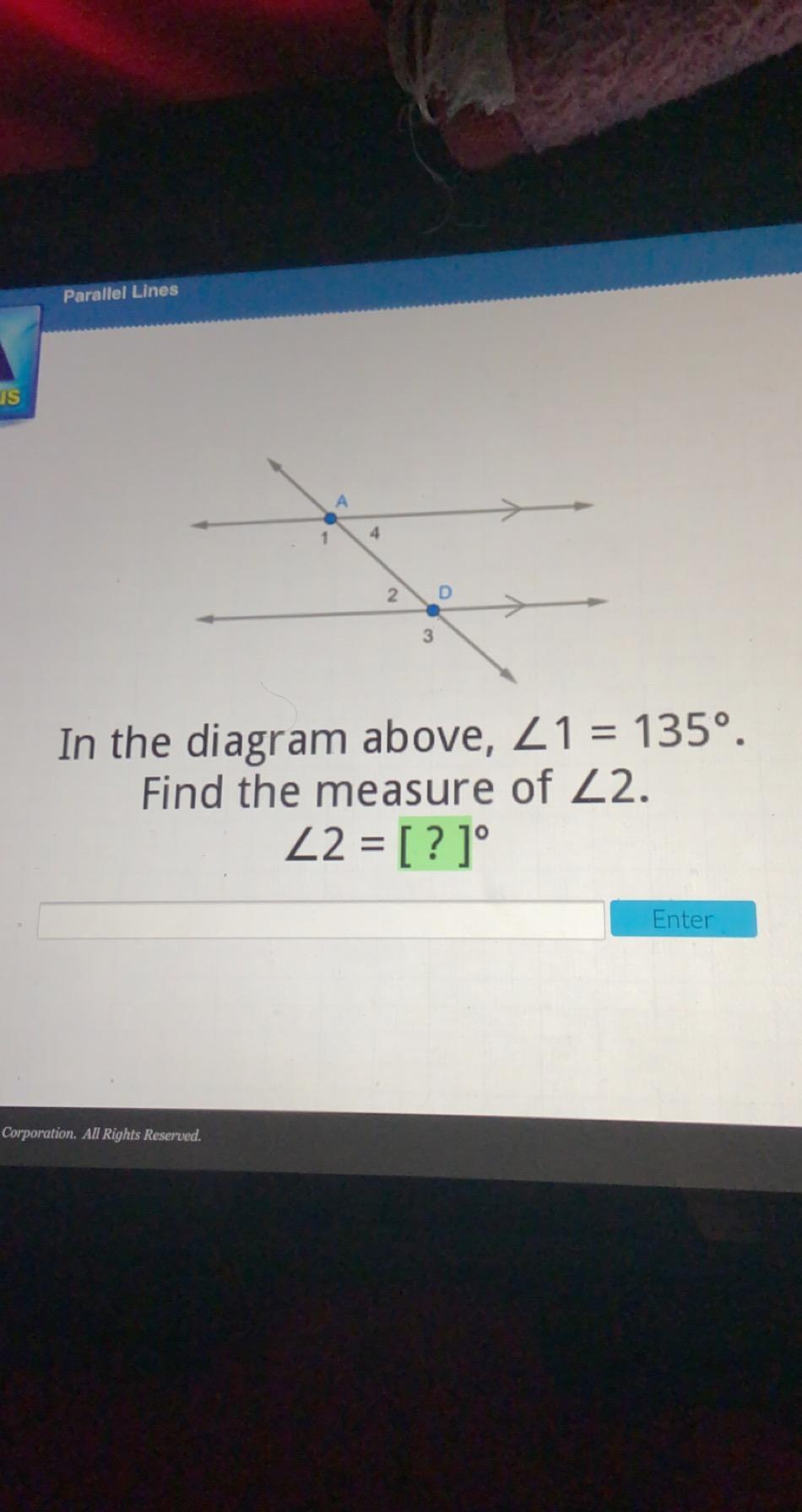
Answers
9514 1404 393
Answer:
∠2 = 45°
Step-by-step explanation:
Angles 1 and 2 are same-side interior angles where the transversal crosses parallel lines. That means they are supplementary angles.
∠1 +∠2 = 180° . . . . . supplementary angles total 180°
135° +∠2 = 180° . . . . substitute the given value
∠2 = 180° -135° . . . . subtract 135°
∠2 = 45°
whats the sum to 4/6 4/6
Answers
In the given problem, the sum of \(\frac{4}{6}\) and \(\frac{4}{6}\) is \(\frac{4}{3}\).
The sum is the result of adding two or more numbers or terms. In other words, it is the process of bringing two or more numbers together to produce a new result or total. The symbol for the sum is "+".
The sum can be performed on any kind of number, including whole numbers, integers, rational numbers, real numbers, and complex numbers. The rules for addition are the same for all types of numbers.
To find the sum of \(\frac{4}{6}\) and \(\frac{4}{6}\),
\(\frac{4}{6}\) + \(\frac{4}{6}\) = 2 \(\times \ \frac{4}{6}\)
= \(\frac{4}{3}\).
So, \(\frac{4}{6}\) + \(\frac{4}{6}\) = \(\frac{4}{3}\).
Learn more about Sum here:
https://brainly.com/question/33719310
#SPJ6
mark draws one card from a standard deck of 52. he receives $ 0.50 for a club, $ 0.65 for an ace and $ 0.95 for the ace of clubs. how much should he pay for one draw?
Answers
The expected payout for one draw is $0.19327.
To calculate how much Mark should pay for one draw, we need to determine the probability of drawing each type of card and the corresponding payouts, and then take a weighted average.
There are 13 clubs in the deck, so the probability of drawing a club is 13/52 = 1/4. The payout for a club is $0.50.
There are 4 aces in the deck, so the probability of drawing an ace is 4/52 = 1/13. The payout for an ace is $0.65.
There is only one ace of clubs in the deck, so the probability of drawing the ace of clubs is 1/52. The payout for the ace of clubs is $0.95.
To calculate the weighted average payout, we can multiply the probability of each outcome by its corresponding payout, and then add up the products:
(1/4) x $0.50 + (1/13) x $0.65 + (1/52) x $0.95 = $0.125 + $0.05 + $0.01827
So the expected payout for one draw is $0.19327.
Learn more about Probability:
https://brainly.com/question/9793303
#SPJ4
An angle measures 18.6° less than the measure of its complementary angle. What is the measure of each angle?
Answers
Answer:
X = 35.7 Y=54.3
Step-by-step explanation:
Let the 2 angles be called X and Y were X is the smaller angle
we know that both angles are complementary therefore
X+Y=90
X = Y - 18.6 ( Given )
Y - 18.6 + Y = 90 ( substitution)
2Y = 90 + 18.6
Y = 108.6/2
Y=54.3
X= Y-18.6= 54.3-18.6 = 35.7
Check : X + Y = 35.7+54.3=90
How to calculate E=mc²
I will give BRAINIEST for whoever has the best solution .
Thank You !!!
Answers
E=mc² is the legendary equation of Albert Einstein .
In the formula
E=mc²Here
E stands for energy emitted.
m stands for mass
c stands for speed of light
C is taken as 3×10^8 m/sm is taken in terms of KgE has units J or KJAnswer:
Equation of Special Relativity
\(\large \text{$ E=mc^2 $}\)
where:
E = energy (measured in Joules)m = mass (measured in kilograms)c = speed of light (a constant) where \(c \approx3 \times 10^{8} \sf \:\:ms^{-1}\)Albert Einstein's famous equation demonstrates the relationship between mass and energy.
It is vital when using this equation that all components are converted (where necessary) into the SI units given above. Therefore, mass must be measured in kilograms and energy must be measured in Joules.
Joules is an SI measurement for energy and is measured as kilograms x meters squared per seconds squared → \(\sf kg \times m^2s^{-2}\)
The SI base units are the standard units of measurement defined by the International System of Units (SI).
A college basketball player makes 80% of his free throws . Over the season he will attempt 100 free throws assume free throw attempts are independent , and let X be the total number of free throws he makes . a) The mean of X is ? Which on is correct -Cannot be determined / 80 /100 /0.80 ? b) The standard deviation of X is ? Which on is correct= 16/ 4/ 80/ 20? c) The probability that the basketball player makes at least 90 of these attempts is approximately ? Which on is correct= 0.0062/ 0.9938/ 0.2660 ? d) If the basketball player instead attempts only 10 free throws, the probability that he makes at most 4 of these is ? Which on is correct= 0.0009/ 0.9991/ 0.0064/ 0.9936?
Answers
A collegiate basketball player hits 80% of his free throw attempts. Assuming free throw attempts are independent, he will try 100 free throws this season the answers are as follows:
a) The mean of X is 80.
b) The standard deviation of X is 4.
c) The probability that the basketball player makes at least 90 of these attempts is approximately is 0.0062.
d) If the basketball player instead attempts only 10 free throws, the probability that he makes at most 4 of these is 0.0064.
As per the question given,
a) The mean of X is given by the formula: mean = n * p, where n is the number of trials and p is the probability of success on each trial. In this case, the player attempts 100 free throws with a probability of success of 0.8, so the mean is:
mean = 100 * 0.8 = 80
Therefore, the correct answer is 80.
b) The standard deviation of X is given by the formula: standard deviation = sqrt(n * p * (1 - p)). Substituting the values, we get:
standard deviation = sqrt(100 * 0.8 * 0.2) = 4
Therefore, the correct answer is 4.
c) To find the probability that the player makes at least 90 free throws, we can use the normal approximation to the binomial distribution. The mean is 80 and the standard deviation is 4, so we can standardize the value of X as follows:
z = (90 - 80) / 4 = 2.5
Using a standard normal distribution table, we can find the probability that Z is greater than 2.5, which is approximately 0.0062.
Therefore, the correct answer is 0.0062.
d) If the player attempts only 10 free throws, the number of successful attempts X follows a binomial distribution with n=10 and p=0.8. The probability that he makes at most 4 of these attempts is:
P(X <= 4) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4)
Using the binomial distribution formula, we can calculate each of these probabilities and sum them up. Alternatively, we can use a binomial probability table or a calculator to find the cumulative probability.
Using a binomial probability calculator, we get:
P(X <= 4) = 0.0064 (rounded to four decimal places)
Therefore, the correct answer is 0.0064.
For such more questions on Probability
https://brainly.com/question/25870256
#SPJ4
What is the equation of the line that passes through the point (-6,1) and has a slope of 1/6?
Answers
Answer:
y - 1 = 1/6x + 1 <<< Point slope form
y = 1/6x + 2 <<< slope intercept form
Either one works unless the question specifies the form of the equation
Step-by-step explanation:
Point slope form: (y - y1) = m(x - x1)
Given: (-6,1) ; m = 1/6
(y - 1) = 1/6(x - (-6))
y - 1 = 1/6x + 1 <<< Point slope form
y = 1/6x + 2 <<< slope intercept form: y = mx + b
8. Use power series multiplication to find the first three terms of the Maclaurin series for f(x)=e^x In(1 - x).
Answers
The first three terms of the Maclaurin series for f(x) = e^x * ln(1 - x) are: f(x) ≈ -x - (3x^2)/2 - (5x^3)/6
To find the first three terms of the Maclaurin series for f(x) = e^x * ln(1 - x), we will first find the Maclaurin series for each individual function and then use power series multiplication.
1. Maclaurin series for e^x:
e^x = 1 + x + (x^2)/2! + ...
2. Maclaurin series for ln(1 - x):
ln(1 - x) = -x - (x^2)/2 - (x^3)/3 - ...
Now, we will multiply the two Maclaurin series:
f(x) = (1 + x + (x^2)/2! + ...) * (-x - (x^2)/2 - (x^3)/3 - ...)
To find the first three terms, we only need to consider the following multiplications:
- (1 * -x)
- (1 * -(x^2)/2) and (x * -x)
- (1 * -(x^3)/3) and (x * -(x^2)/2)
Performing these multiplications:
- (1 * -x) = -x
- (1 * -(x^2)/2) + (x * -x) = -(x^2)/2 - x^2 = -3x^2/2
- (1 * -(x^3)/3) + (x * -(x^2)/2) = -(x^3)/3 - (x^3)/2 = -5x^3/6
So, the first three terms of the Maclaurin series for f(x) = e^x * ln(1 - x) are:
f(x) ≈ -x - (3x^2)/2 - (5x^3)/6
To know more about Maclaurin series, visit:
https://brainly.com/question/24188694#
#SPJ11
Hector has a bag of colored candies with the following colors: 12 orange, 4 yellow, 10 green, 4 red, 8 blue, 7 purple, and 11 pink. Without looking, Hector pulls a candy out of the bag. What is the probability Hector pulls out a yellow or green candy?
Answers
Answer:
10/13
Step-by-step explanation:
total candies = 62
yellow and green candies = 20
P (yellow or green candies) = 20/62
=> 10/13
Solve for x. Enter the solutions from least to greatest. Round to two decimal places. (x-6)^2-5=0 lesser x= , greater x=
Answers
Answer: lesser x = 3.76 & greater x = 8.24
Step-by-step explanation: just took the test
For the given quadratic equation lesser x=3.765 and greater x=8.235.
The given quadratic equation is (x-6)²-5=0.
We need to find the solutions from least to greatest.
What is the formula to find the solution to the quadratic equation?The formula to find the solution to the quadratic equation is \(x=\frac{-b\pm\sqrt{b^{2}-4ac }}{2a}\).
Now, (x-6)²-5=0 can be written as x²-12x+31=0
Here, a=1, b=-12 and c=31
x=(12±√20)/2
⇒x=(12±4.47)/2
⇒x=3.765 or x=8.235
Therefore, lesser x=3.765 and greater x=8.235.
To learn more about the solution of quadratic equation visit:
https://brainly.com/question/17376136.
#SPJ2
Given the triangle below with centroid G, determine the following values.
If EG=3.5, then GB= and BE= If AD=15, then AG= and DG= If CG=6x, then FG- and CF=

Answers
Answer:
GB = 7
BE = 10.5
AG = 10
DG = 5
FG = 3·x
CF = 9·x
Step-by-step explanation:
The given parameters are;
The centroid of the ΔABC = G
Segments CF, BE, and AD are median lines
EG = 3.5 Given
∴ EG = 1/3 × BE by definition of the properties of median line
∴ BE = 3 × EG = 3 × 3.5 = 10.5
BE = 10.5
GB = 2/3 × BE = 2/3 × 10.5 = 7 by definition of the properties of median line BE
GB = 7
Similarly;
Given that AD = 15, AG = 2/3 × AD = 2/3 × 15 = 10 by definition of the properties of median line AD
AD = 10
DG = 1/3 × AD = 1/3 × 15 = 5 by definition of the properties of median line AD
DG = 5
Similarly;
Given CG = 6·x
FG = 1/3 × CF
CF = 3 × FG
CG = 2/3 × CF = 2/3 × 3 × FG
∴ CG = 2 × FG
FG = CG/2 = 6·x/
2 = 3·x
FG = 3·x
CF = 3 × FG = CF = 3 × 3 × x = 9·x
CF = 9·x
A student is trying to construct triangles using four different sets of angles. Th angles in each set are given below. Which set will allow the student to construct a triangle

Answers
Well I can't be for sure but I know for a fact its not set IV it's not possible to make a triangle out of all right angles. Set II, well, that isn't right either. You can't make a triangle out of all obtuse angles. Like the right angle one, its not possible you can only use one obtuse or right angle in a triangle other wise it's not going to be a triangle. I'd say go try Set III since that would most likely make an equilateral triangle.
need answer fast in 5 minutes

Answers
Answer:
Each term in pattern B is 9 less than the corresponding term in pattern A.
How many square tiles with sides of 30 cm are needed to cover a floor with an area of 36m²?
Answers
Answer:
400 tiles
Step-by-step explanation:
Calculate the area of each tile, in m^2:
30 cm = 0.30 m
(0.30 m)^2 = 9.0 x 10^-2 m^2
Divide this into the total area:
(36m^2)/(9.0 x 10^-2 m^2)= 400 tiles
====
Another approach is to note that 6m^2 could be envisioned as a square with sides of 6 m. Calculate the tiles needed to stretch along one side:
6 m = 600 cm
600 cm/30 cm = 20 tiles
It takes 20 tiles to cover one direction
It would also take 20 tiles for the other direction, so a mosaic of 20 by 20 tiles would cover the 36 m^2.
20 x 20 = 400 tiles
Find the equation of the line that passes through (-1,-3) and is perpendicular to 2 y = x − 3 . Leave your answer in the form y = m x + c
Answers
Answer:
Remember that the slope of perpendicular lines are negative reciprocals of each other.Step-by-step explanation:y = 1 - 2x the slope is -2 the value of the x term.So the slope of the new line using point (- 1, 2) is 1/2.Now use y = mx + b where y = -1, x = 2, and m = 1/2 .y = mx + b-1 = 1/2(2) + b solve for "b", the y-intersect-1 = 1 + b-2 = bThe line that is perpendicular to y = 1 - 2x is y = 1/2x - 2
Step-by-step explanation:
What is the sign of b/c

Answers
Answer:
Negative.
Step-by-step explanation:
b is above zero. So, it is positive.
c is below zero. So, it is negative.
A positive divided by negative number results in negative.
Answer:
B. negative
Step-by-step explanation:
-2 is negative. That's why.
5k/6 + 2/3 = 4/5
Wrote in image and in text, pls help

Answers
Answer:
\(\frac{4}{5}\)
Step-by-step explanation:
Step 1: Write the equation
\(\frac{5k}{6}\) + \(\frac{2}{3}\) = \(\frac{4}{3}\)
Step 2: Multiply each term by the lowest common multiple (lcm)
lcm of the denominators 6 and 3 = 6
Step 3:
6x\(\frac{5k}{6}\) + 6x\(\frac{2}{3}\) = 6x\(\frac{4}{3}\)
Next
5k + 4 = 8
5k = 8 - 4
5k = 4
Divide through by 5
k = \(\frac{4}{5}\)
A group of neighbors is holding an end of summer block party. They buy ppp packs of hot dogs, with 888 hot dogs in each pack. All together, they have 565656 hot dogs for the party.
Write an equation to describe this situation.
How many packs of hot dogs did the neighbors buy?
Answers
Answer:
565656÷8=p
So the answer is 637:D
Decimal multiplier by 1.7%
Answers
Answer:
times by 1.17
Step-by-step explanation:
hope this helps!
please give me a brainliest!!<3
Answer: 0.017
Step-by-step explanation:
1.7% = 0.017
evaluate the following expression. you should do this problem without a calculator e^In3
Answers
The relation between the exponential and the logarithm is used. Then the expression \(e^{\ln3}\) is given as 3.
What is a logarithm?Exponents can also be written as logarithms. A number base logarithm is similar to some other number. It is the exact inverse of the exponent expression.
The expression is given below.
\(\rightarrow e^{\ln3}\)
We know the formula
\(\rm e^{\ln x} = x\)
Then the expression can be written as
\(e^{\ln3} = 3\)
More about the logarithm link is given below.
https://brainly.com/question/7302008
#SPJ1
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. 9. y= x
,y=0,x=4
Answers
The volume generated by rotating the region bounded by the curve y = x about the y-axis using the method of cylindrical shells is 486π cubic units.
To find the volume generated by rotating the region bounded by the curve y = x about the y-axis using the method of cylindrical shells, we can follow these steps:
First, let's sketch the region bounded by the curve y = x. This is a straight line passing through the origin with a slope of 1. It forms a right triangle in the first quadrant, with the x-axis and y-axis as its legs.
Next, we need to determine the limits of integration. Since we are rotating about the y-axis, the integration limits will correspond to the y-values of the region. In this case, the region is bounded by y = 0 (the x-axis) and y = x.
The height of each cylindrical shell will be the difference between the upper and lower curves. Therefore, the height of each shell is given by h = x.
The radius of each cylindrical shell is the distance from the y-axis to the x-value on the curve. Since we are rotating about the y-axis, the radius is given by r = y.
The differential volume element of each cylindrical shell is given by dV = 2πrh dy, where r is the radius and h is the height.
Now we can express the volume of the solid of revolution as the integral of the differential volume element over the range of y-values:
V = ∫[a, b] 2πrh dy
Here, [a, b] represents the range of y-values that define the region. In this case, a = 0 and b = 9 (as y = x, so the curve intersects y-axis at y = 9).
Substituting t
he values of r and h into the integral, we have:
V = ∫[0, 9] 2πy(y) dy
Simplifying, we get:
V = 2π ∫[0, 9] y^2 dy
Evaluating the integral, we have:
V = 2π [y^3/3] from 0 to 9
V = 2π [(9^3/3) - (0^3/3)]
V = 2π [(729/3) - 0]
V = 2π (243)
V = 486π
to learn more about integration.
https://brainly.com/question/31744185
#SPJ11
1) Which expression is equivalent to 4 - (-7)?A 7 + 4B 4 - 7C-7-4D - 4 + 7
Answers
Answer:
\(4-(-7)=7+4\)Explanation:
Given the expression;
\(4-(-7)\)simplifying;
\(-\times-=+\)we have;
\(4+7=7+4\)Therefore;
\(4-(-7)=7+4\)Arthur has x pennies. His father gave him 6 dimes, and his mother gave him 4 nickels. Which expression represents the number of coins Arthur has now?
a) x+80
b) x+10
c) 6x+4
d) 4x+6
Answers
The expression x + 80 represents the number of coins Arthur has now, since he x pennies and an additional 6 dimes and 4 nickels.
How to calculate for the number of coinsWe shall convert the pennies, dimes and nickels into same unit before adding to get the expression for the number of coins Arthur will have in total.
A penny = 1 cent, so
x pennies = x cents
A dime = 10 cents so;
6 dimes = 6 × 10cents
6 dimes = 60 cents
A nickel = 5 cents so;
4 nickels = 4 × 5 cents
4 nickels = 20 cents
Arthur's coins in total = (x + 60 + 40) cents
Arthur's coins in total = (x + 80) cents.
Therefore, the expression expression x + 80 represents the number of coins Arthur will have in total, wether in pennies, dimes or nickels.
Learn more about pennies, nickels and dimes here: https://brainly.com/question/5193496
#SPJ1