Showing each step... use the product rule to simplify the following monomial.
INCLUDE ANY STEP THAT SHOWS HOW EXPONENTS ARE CHANGING (for example,
exponents adding, subtracting, multiplying, etc.).
Show Your Work
3a4 . 5a³
Answers
Related Questions
In a baseball game, Elena scored twice many pints as Tyler.Tyler scored four points fewer than Noah, and Noah scored three times as many points as Mai. If Mai scores 5 points, how many did Elena scored?
Answers
Answer:
Elena scored 22 points.
Step-by-step explanation:
Mai scored 5 points, and Noah scored three times as many. This means Noah scored 15 points and if Tyler scored four points fewer, he scored 11 points. If Elena scored twice as many as Tyler, she scored 22.
consider a two-factor factorial design with three levels for facts a, three levels for factor b, and four replicates in each of the nine cells
a. how many degrees of freedom are there in determining the A variation and the factor B variation
b. how many degrees of freedom are there in dreaming the interaction variation
c. how many degrees of freedom are there in determining the random variation
d. how many degrees of freedom are there in determining the total variation
Answers
In calculating the factor A variation, there are two degrees of freedom. In determining the variation of factor B, there are two degrees of freedom.
What is a two-factorial design?A two-factor factorial design is an experiment that collects data for all potential values of the two factors of the study. The design is a balanced two-factor factorial design if equivalent sample sizes are used for every of the possible factor combinations.
Suppose we have two components, A and B, each of which has a high number of levels of interest. We will select a random level of component A and a random level of factor B, and n observations will be taken for each experimental combination.
From the data given:
a.
In calculating the factor A variation, there are two degrees of freedom.
In determining the variation of factor B, there are two degrees of freedom.
b.
Finding the degree of freedom using the interaction variation, there are four degrees of freedom.
c.
In finding the random variable, there are 9(4-1) = 27 degrees of freedom.
d.
In calculating the total variable, there are 9*4-1 =35 degrees of freedom.
Learn more about using a two-factor factorial design for determining the degree of freedom here:
https://brainly.com/question/14292694
#SPJ1
how do you fin x using the equation y=1 .5 x
Answers
Answer:
BY dividing by 1.5
Step-by-step explanation:
Since the variable is next to the number that multiplication so you would do inverse operation!
Answer: Possible answers:
- Isolating the varible
- Dividing both sides of the equation by 1.5
- x = \(\displaystyle \frac{y}{1.5}\)
Step-by-step explanation:
In this case, "finding x" will be setting the equation equal to x. In other words, we will isolate the variable x.
To do this, we will divide both sides of the equation by 1.5. Sine the x is being multiplied by 1.5, the inverse operation of multiplication is division.
y = 1.5x
\(\frac{y}{1.5}\) = \(\frac{1.5x}{1.5}\)
\(\frac{y}{1.5}\) = 1x
\(\frac{y}{1.5}\) = x
x = \(\displaystyle \frac{y}{1.5}\)
Graph the function y=2-VX+1. What is the missing x-coordinate for the point (x,- 1.24), to the nearest tenth?
06.1
07.3
O 8.4
0 9.5
Answers
Answer:
It's 0.61
Step-by-step explanation:
I graphed the equation and got 0.61 on the x axis when the y value was 1.24
The missing x-coordinate is 9.5. The correct answer is option D.
What is a function?
A function in mathematics set up a relationship between the dependent variable and independent variable. on changing the value of the independent variable the value of the dependent variable also changes.
The given function \(y = 2 -\sqrt{x+1}\) and the point are ( x, -1.24 ). Put y = -1.24 in the given equation to get the value of x.
\(y = 2 -\sqrt{x+1}\)
\(-1.24 = 2 - \sqrt{x+1}\\-1.24 - 2 = \sqrt{x+1}\\-3.24 = \sqrt{x+1}\)
Squaring on both sides.
\((-3.24)^2 = (\sqrt{x+1})^2\)
10.5 = x + 1
x = 9.5
Hence, the correct option is D.
To know more about function follow
https://brainly.com/question/2833285
#SPJ2
A university is interested in determining the average statistics anxiety score for all undergraduate students in the U.S. For a random sample of 33 undergraduate students, it is found that the average average statistics anxiety score is 39.4 with a standard deviation of 0.9. Assume that the statistics anxiety scores for all undergraduate students in the U.S is normally distributed. A 98% confidence interval for the true mean statistics anxiety score μ is closest to.
Answers
The 98% confidence interval for the true mean statistics anxiety score (μ) is approximately (39.037, 39.763).
To calculate the 98% confidence interval for the true mean statistics anxiety score (μ) for all undergraduate students in the U.S., we can use the formula:
Confidence interval = sample mean ± (critical value * standard error)
First, we need to find the critical value associated with a 98% confidence level. Since we are assuming a normal distribution, we can use the Z-table or a statistical software to find this value. For a 98% confidence level, the critical value is approximately 2.33.
Next, we calculate the standard error (SE) using the formula:
SE = standard deviation / √sample size
In this case, the standard deviation is 0.9 and the sample size is 33. Plugging these values into the formula, we get: SE = 0.9 / √33 ≈ 0.156
Now, we can calculate the confidence interval:Confidence interval = 39.4 ± (2.33 * 0.156)
Simplifying the expression:Confidence interval ≈ 39.4 ± 0.363
This gives us the interval (39.037, 39.763). This means we are 98% confident that the true mean statistics anxiety score for all undergraduate students in the U.S. falls within this interval.
for more search question interval
https://brainly.com/question/20309162
#SPJ8
Classify the two given samples as independent or dependent. Sample 1: Pre-training blood pressure of 17 people Sample 2: Post-training blood pressure of 17 people a. dependent b. independent
Answers
Answer:
Sample 1 : independent
Sample 2 : dependent
Step-by-step explanation:
From the question we are told that
The given date is
Sample 1: Pre-training blood pressure of 17 people
Sample 2: Post-training blood pressure of 17 people
Now Sample 1 is independent because the Pre-training blood pressure of 17 people does not depend of Post-training blood pressure of 17 people
While
Sample 2 is dependent because the Post-training blood pressure of 17 people is dependent on the Pre-training blood pressure of 17 people
PLEASE HELP ME FIND THE SLOPE!
Answers
To find slope, what we need to do is calculate rise/run beginning at the y-intercept, which is also known as the point where the line crosses the y-axis. The y-intercept is (0, 3).
With this in mind, we can calculate rise (which is how we move vertically) and run (which is how we move horizontally):
The point moves down 1 unit, which means the slope is negative. It moves 2 units to the right, which means the slope is -1/2.
The slope intercept form equation would look like:
y = -1/2x + 3
Answer Recap: The slope is -1/2.
PLEASE HELP ASAP
The diagrams show a polygon and the image of the polygon after a transformation.
Use the diagrams to determine which statements are true. Select all statements that are true.
Answers
The correct statements regarding the transformations are given as follows:
Parallel lines will always be parallel after a reflection.Lines that are not parallel will never be parallel after a translation.What are transformations on the graph of a function?Examples of transformations are given as follows:
A translation is defined as lateral or vertical movements.A reflection is either over one of the axis on the graph or over a line.A rotation is over a degree measure, either clockwise or counterclockwise.For a dilation, the coordinates of the vertices of the original figure are multiplied by the scale factor, which can either enlarge or reduce the figure.Parallel lines are lines that have the same slope, that is, lines that do not intercept, and the transformations do not change whether the lines are parallel or not.
More can be learned about transformations in a figure at https://brainly.com/question/28687396
#SPJ1
Analyze the diagram below and complete the instructions that follow.
8
45°
Find the value of x.
A. 4
B. 8√√2
2
C. 4√2
DG
45°
Save and Exit
Next
Subr
Answers
Answer:
Based on the diagram, we can see that the triangle formed by the line segment with length 8 and the two dashed line segments is a right triangle with a 45° angle. This means that the other two angles of the triangle are also 45° each.
Using the properties of 45°-45°-90° triangles, we know that the length of the hypotenuse is equal to the length of either leg times the square root of 2. Therefore, we have:
x = 8 / sqrt(2) = 8 * sqrt(2) / 2 = 4 * sqrt(2)
So the value of x is option B: 8√2 / 2 or simplified, 4√2.
SUBTRACT the given polynomials : (x + 2) - (8x + 4)
A}7x + 2
B}7x - 2
C}-7x - 2
D}-7x + 2
WELP ;-;
Answers
The equivalent expression for the subtraction (x + 2) - (8x + 4) is -7x - 2
Option C is correct
The given polynomial expression is:
(x + 2) - (8x + 4)
Expand the expression by removing the parenthesis
x + 2 - 8x - 4
Collect like terms
x - 8x + 2 - 4
-7x - 2
Therefore, the equivalent expression for the subtraction (x + 2) - (8x + 4) is -7x - 2
Learn more on polynomials here:
https://brainly.com/question/16058963
If triangles ABC and DEF are similar, what is y? Show your work.
Answers
The value of y is 18
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The angles of the two triangle must be equal and it not necessary they have equal sides.
Therefore the corresponding angles of similar triangles are congruent and the ratio of corresponding sides of similar triangles are equal.
Therefore;
14/21 = 12/y
14y = 21 × 12
14y = 252
divide both sides by 14
y = 252/14
y = 18
Therefore the value of y is 18.
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
Match the information on the left with the appropriate equation on the right.
An equation perpendicular to y = - 3x + 1 through the point
(3,-2)
An equation through the point ( - 2, 3) and parallel to
y = - 3x - 1
Answers
Is the answer True or false
Answers
Answer:
true
Step-by-step explanation:
true
Can someone help me answer this
Answers
Step-by-step explanation: \(2x^{2} +3x+5=0\\\\x=-3±\sqrt{b^{2}-4ac} /2a\\x=-3±\sqrt{3^2-4*2*5/2*2}\\\\x=-3/4 ± \sqrt{31} * (1/4*i)\\x=-3/4 + \sqrt{31} * (-1/4*i)\\\)
Answer: Using the Quadratic Formula, the answer would be x = -3/4 + \sqrt{31} * ([-]1/4*i)
Can I call you lease have some help with this problem
Answers
Question:
Solution:
Consider the following polynomial function:
\(h(x)=2x^3+23x^2+58x-35\)Since all coefficients are integers, we can apply the rational zeros theorem.
the rational zeros theorem states:
If h(x) is a polynomial with integer coefficients and if P/Q is a zero of h(x), then P is a factor of the constant term of h(x) and Q is a factor of the leading coefficient of h(x).
Now, the trailing coefficient (the coefficient of the constant term) is -35.
its factors (with the plus sign and the minus sign) are:
\(\pm1,\text{ }\pm5,\text{ }\pm7,\text{ }\pm35\)These are the possible values for P.
The leading coefficient (the coefficient of the term with the highest degree) is 2.
its factors (with the plus sign and the minus sign) are:
\(\pm1,\text{ }\pm2\)These are the possible values for Q.
Thus, all possible values of P/Q are:
\(\frac{P}{Q}\colon\text{ }\pm\frac{1}{1}\text{ , }\pm\frac{1}{2}\text{ , }\pm\frac{5}{1},\text{ }\pm\frac{5}{2}\text{ , }\pm\frac{7}{1},\text{ }\pm\frac{7}{2},\text{ }\pm\frac{35}{1},\text{ }\pm\frac{35}{2}\)now simplify and remove the duplicates (if any). These are the possible rational roots:
\(\pm1,\text{ }\pm\frac{1}{2}\text{ , }\pm5,\text{ }\pm\frac{5}{2},\text{ }\pm7,\text{ }\pm\frac{7}{2},\text{ }\pm35,\text{ }\pm\frac{35}{2}\)Next, check the possible roots: if a is a root of the polynomial h(x), the remainder from the division of h(x) by x-a should equal 0. According to the remainder theorem, this means that
\(h(a)=0\)Check 1: divide h(x) by x-1:
\(h(1)=48\)thus, the remainder is 48.
Check -1: divide h(x) by x+1:
\(h(-1)=-72\)
thus, the remainder is -72.
Check 1/2: divide h(x) by x-(1/2):
\(h(\frac{1}{2})=0\)
thus, the remainder is 0. Hence 1/2 is a root.
Check -1/2: divide h(x) by x+(1/2):
\(h(-\frac{1}{2})=-\frac{117}{2}\)
thus, the remainder is -117/2.
Check 5: divide h(x) by x-5:
\(h(5)=1080\)
thus, the remainder is 1080.
Check -5: divide h(x) by x+5:
\(h(-5)=0\)
thus, the remainder is 0. Hence -5 is a root.
Check 5/2: divide h(x) by x-(5/2):
\(h(\frac{5}{2})=285\)
thus, the remainder is 285.
Check -5/2: divide h(x) by x+(5/2):
\(h(-\frac{5}{2})=-\frac{135}{2}\)
thus, the remainder is -135/2.
Check 7: divide h(x) by x-7:
\(h(7)=2184\)
thus, the remainder is 2184.
Check -7: divide h(x) by x+7:
\(h(-7)=0\)
thus, the remainder is 0. Hence -7 is a root.
Check 7/2: divide h(x) by x-(7/2):
\(h(\frac{7}{2})=\frac{1071}{2}\)
thus, the remainder is 1071/2.
Check -7/2: divide h(x) by x+(7/2):
\(h(-\frac{7}{2})=-42\)
thus, the remainder is -42.
Check 35: divide h(x) by x-35:
\(h(35)=115920\)
thus, the remainder is 115920.
Check -35: divide h(x) by x+35:
\(h(-35)=-59640\)
thus, the remainder is -59640.
Check 35/2: divide h(x) by x-(35/2):
\(h(\frac{35}{2})=\frac{37485}{2}\)
thus, the remainder is 37485/2.
Finally, check -35/2: divide h(x) by x+(35/2):
\(h(-\frac{35}{2})=-4725\)
thus, the remainder is -4725.
We can conclude that the correct answer is:
The zeros of the given function are:
\(\frac{1}{2},\text{ }-5,\text{ -7}\)
There is 60% chance that it will rain today. If it rains, the probability of watching a movie is 0.5. But, if it does not rain then the probability of watching a movie is 0.3. What is the probability of watching a movie today?
Answers
Applying the given probabilities, it is found that there is a 0.42 = 42% probability of watching a movie today.
These following probabilities involve a movie being watched today:
0.5 of 0.6(if it rains today).0.3 of 1 - 0.6 = 0.4(if it does not rain today).Hence, adding them:
\(p = 0.5(0.6) + 0.3(0.4) = 0.3 + 0.12 = 0.42\)
0.42 = 42% probability of watching a movie today.
A similar problem is given at https://brainly.com/question/14398287
Estimate a 15% tip on a dinner bill of $79.24 by first rounding the bill amount to the nearest ten dollars.
Answers
Hope it helps!
What is the answer help
Answers
Answer: 162°
Step-by-step explanation:
To find the answer to this question, we need to find what 45% of 360 degrees (a circle) is.
First, a percent divided by 100 becomes a decimal.
45% / 100 = 0.45
Next, "of" means multiplication in mathematics.
0.45 * 360 = 162
The central angle will be 162°.
Solve following modular equation, using reverse Euclidean algorithm:
\((5 * x) mod 91 = 32\)
Answers
The required reverse Euclidean algorithm is the solution to the modular equation (5x) mod 91 is
x = 6(mod 91).
Given that (5*x) mod 91 =32.
To solve the modular equation (5*x) mod 91 =32 using reverse Euclidean algorithm is to find the modular inverse of 5 modulo 91.
Consider (5*x) mod 91 =32.
5x = 32(mod 91)
Apply the Euclidean algorithm to find GCD of 5 and 91 is
91 = 18 * 5 + 1.
Rewrite it in congruence form,
1 = 91 - 18 *5
On simplifying the equation,
1 = 91 (mod 5)
The modular inverse of 5 modulo 91 is 18.
Multiply equation by 18 on both sides,
90x = 576 (mod91)
To obtain the smallest positive solution,
91:576 = 6 (mod 91)
Divide both sides by the coefficient of x:
x = 6 * 90^(-1).
Apply the Euclidean algorithm,
91 = 1*90 + 1.
Simplify the equation,
1 + 1 mod (90)
The modular inverse of 90 modulo 91 is 1.
Substitute the modular inverse in the given question gives,
x = 6*1(mod 91)
x= 6 (mod91)
Therefore, the solution to the modular equation (5x) mod 91 is
x = 6(mod 91).
Learn more about modular equation click here:
https://brainly.com/question/15055095
#SPJ1
is x=y^2 a function or not
Answers
Answer:yes
Step-by-step explanation:
—
what's .612 with twelve repeating as a fraction in its simplest form?
Answers
Answer:
101/165
Step-by-step explanation:
Answer:
101/165
Step-by-step explanation:
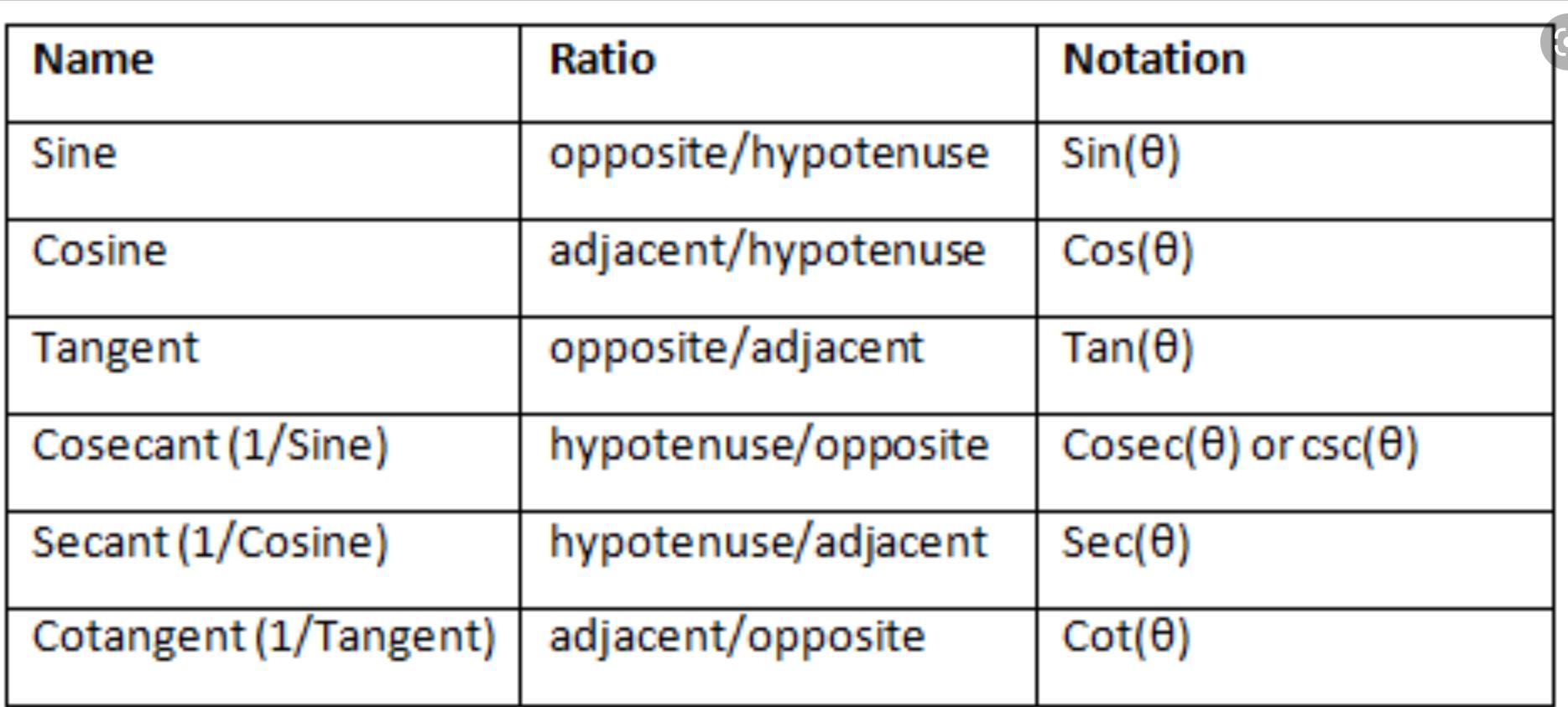
What are the trigonometric ratios? Write all six.
Answers
Step-by-step explanation:
Check that attachment
Hope it helps :)
Hey! :)
________ ☆ ☆_________________________________________
Answer:
There are six trigonometric ratios, which will be under “Explanation”
Step-by-step explanation:
Trigonometric ratios are a measurements of a right triangle.
Here are the all the six trigonometric ratios.
1. cotangent (cot)
2. cosecant (csc)
3. cosine (cos)
4. secant (sec)
5. sine (sin)
6. tangent (tan)
Hope this helps! :)
_________ ☆ ☆________________________________________
By, BrainlyMember ^-^
Good luck!
At noon, a tank contained 20 in. of water. After several hours, it contained 16 in. of water. What is the percent decrease of water in the tank
Answers
Answer:
20 percent decrease
Step-by-step explanation:
it lost 4 inches of water (20-16) and 4 is a fifth of 20. a fifth is 20 percent so it is a 20 percent decrease
6.1/5(12b+5) for b = 5/6
Answers
Answer:
Step-by-step explanation:
6.1 / 5 ( 12b + 5 )
b = 5/6
by substituting,
6.1 / 5 ( 12 × 5/6 + 5 )
1.22 × 15
= 18.3
Hope this helps
plz mark as brainliest!!!!!!!
Stay safe!!
For the diagram shown, find the measures of angles 4,5, and 6.
Answers
Answer:
wheres the diagram???
Step-by-step explanation:
Miles is buying a chair that regularly costs $250. Today the chair is on sale for 30% off. If the tax rate is 6%, what is the sale price of the chair including tax?
Answers
Answer:
not sure
Step-by-step explanation:
I give brainliest :)
Answers
Explanation:
11. Martin's suitcase has a volume of 1,080 cubic inches. Lily's suitcase measures 9 inches wide, 13 inches long, and 21 inches high. What is the combined volume of the two suitcases?
Answers
Answer: 3,348 cubic inches
Step-by-step explanation:
1. Since we know that volume= length x width x height, then we can plug our values into this equation.
2. So, we would do volume= 9 x 12 x 21.
3. 9 x 12 = 108, and 108 x 21 =2,268.
4. Now that we have both of the volumes, we have to add them together.
5. 1,080 + 2,268 = 3,348
6. The combined volume is 3,348 cubic inches.
(6m-7)x4. Please help meeee
Answers
Answer:
=6mx^4−7x^4
Step-by-step explanation:
(6m−7)(x^4)
=(6m+−7)(x^4)
=(6m)(x^4)+(−7)(x^4)
\(\huge\text{Hey there!}\)
\(\mathsf{(6m - 7)\times4}\)
\(\mathsf{= (6m - 7)(4)}\)
\(\mathsf{= (6m - 7) 4}\)
\(\mathsf{= 4(6m - 7)}\)
\(\mathsf{= 4(6m) - 4(-7)}\)
\(\mathsf{= 6m(4) + (-7)(4)}\)
\(\mathsf{= 6m(4) - 7(4)}\)
\(\mathsf{= 6m - 28}\)
\(\huge\textbf{Therefore, your answer should be:}\)
\(\huge\boxed{\frak{24m - 28}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Real numbers a and b satisfy
a + ab = 250
a - ab = -240
Enter all possible values of a, separated by commas.
Answers
The only possible value of "a" that satisfies the given equations is a = 5.
The possible values of "a" that satisfy the given equations, let's solve the system of equations:
a + ab = 250 ---(1)
a - ab = -240 ---(2)
We can solve this system by using the method of substitution. Rearranging equation (2), we get:
a = ab - 240 ---(3)
Substituting equation (3) into equation (1), we have:
(ab - 240) + ab = 250
2ab - 240 = 250
2ab = 250 + 240
2ab = 490
ab = 490/2
ab = 245
Now we have the value of "ab."
We can substitute this back into equation (3) to solve for "a":
a = (245) - 240
a = 5
For similar questions on possible value
https://brainly.com/question/21237643
#SPJ11