Show that Φ (Phi/fa1) uppercase Φ, lowercase φ or ϕ) is onto and one-to-one
Answers
To show that the function Φ (Phi) is onto and one-to-one, we need to establish two properties:
Onto (Surjective):
For a function to be onto, every element in the range must have a preimage in the domain. In other words, for every y in the range, there must exist an x in the domain such that Φ(x) = y.
One-to-one (Injective):
For a function to be one-to-one, distinct elements in the domain must map to distinct elements in the range. In other words, if Φ(x₁) = Φ(x₂), then x₁ = x₂ Let's proceed to show both properties:
Onto (Surjective):
To show that Φ is onto, we need to demonstrate that for every y in the range of Φ, there exists an x in the domain such that Φ(x) = y.
Assuming that Φ(x) = y, we want to find the preimage x in the domain. However, you didn't provide the specific definition or context of the function Φ. Please provide the definition or specify the nature of the function Φ so that I can continue with the proof.
One-to-one (Injective):
To show that Φ is one-to-one, we need to prove that if Φ(x₁) = Φ(x₂), then x₁ = x₂ for any x₁ and x₂ in the domain.
Again, without the specific definition or context of the function Φ, I cannot proceed with the proof for the one-to-one property. Please provide the necessary information, and I'll be happy to help you further.
Learn more about function here:
https://brainly.com/question/11624077
#SPJ11
Related Questions
Answer this question based on the number line shown.
A
B
C
The distance from a point to point Cis 1 and the distance from that same point to point Bis 4. The point must be
goint A
Obetween DandA
point D
Obebween CandA

Answers
Since the distance from a point to point C is 1 and the distance from that same point to point B is 4, the point must be: C. point D.
What is a number line?In Mathematics and Geometry, a number line simply refers to a type of graph with a graduated straight line which comprises both positive and negative numbers that are placed at equal intervals along its length.
This ultimately implies that, a number line primarily increases in numerical value towards the right from zero (0) and decreases in numerical value towards the left from zero (0).
From the number line shown above, we have:
Distance = 4 + (-1)
Distance = 4 - 1
Distance = 3 (point D).
Read more on number line here: brainly.com/question/22515080
#SPJ1
complete the statements in 1996 drop down 1 million DVDs were sold the number DVD so drop down to for the next approximately drop down three years
Answers
A total number of 4 x 10⁶ DVD's were sold in the span of next three years.
What is function?A function is a relation between a dependent and independent variable. We can write the examples of functions as -
y = f(x) = ax + b
y = f(x, y, z) = ax + by + cz
Given is that in 1996, 1 million DVDs were sold.
Since no further information is given, assume that the increase in the sales of the DVD's took place at the same rate every year. So, initially, 1 million DVD's have been sold. So, for the next {x} years, we can write the total number of DVD's sold as -
y = mx + c
y = 10⁶x + 10⁶
y = 10⁶(x + 1)
For {x} = 3, we can write -
y = 4 x 10⁶
Therefore, a total number of 4 x 10⁶ DVD's were sold in the span of next three years.
To solve more questions on functions, visit the link below-
https://brainly.com/question/30194223
#SPJ1
The length of each side of an equilateral triangle is 4 cm longer than the length of each side of a square. If the perimeter of these two shapes is the same, find the area of the square.
Answers
The area of the square is 144 \(cm^{2}\).
Let x be the side of the square. Then the length of the triangle is (x+4). Perimeter is the length of all sides of a geometric figure combined. For an equilateral triangle, it's equal to thrice the length of one side. For a square, it's four times the length of one side. The Perimeter of the Triangle is 3(x+4) & the Perimeter of the square is 4x.
We know, both these perimeters are equal. Hence,
4x = 3(x+4)
To further simplify the above equation.
4x = 3x + 12
x = 12
Hence, the length of one side of the square is 12 cm. The area of the square can be calculated as follows:
Area = \((side)^{2}\)
Area = 12 * 12
Area = 144 \(cm^{2}\)
Hence, the Area of the Square is 144 \(cm^{2}\)
To know more about Linear Algebra:
https://brainly.com/question/30894110
5 students participated in a push-up competition.
The amount of push-ups each student completed is listed: 12, 7, 10, 11,5
What was the mean number of push-ups?
Answers
Answer: 9
Step-by-step explanation:
Formula : Mean = \(\dfrac{\text{Sum of observations}}{\text{Number of observaions}}\)
Given: 5 students participated in a push-up competition.
The amount of push-ups each student completed is listed: 12, 7, 10, 11,5.
Mean = \(\dfrac{12+7+10+77+5}{5}\)
\(=\dfrac{45}{5}=9\)
Hence, the mean number of push-ups = 9
a rectangle is 5 times as long as it is wide. It’s perimeter is 24 in. How long and how wide is the rectangle?
Answers
The length of the rectangle is 10 inches and the rectangle is 10 inches long and 2 inches wide.
What is perimeter of a rectangle?The total distance around the outside of the rectangle is termed as Perimeter of a rectangle. It is equal to the sum of the lengths of all four sides of the rectangle.
Let's assume that the width as "w" inches.
As per the problem statement, the length of the rectangle is 5 times its width, which means that the length is 5w inches.
The perimeter of a rectangle is :
P = 2(l + w)
Substituting the values, we get:
24 = 2(5w + w)
Simplifying the above equation, we get:
24 = 12w
Dividing both sides by 12, we get:
w = 2
So, the width of the rectangle is 2 inches.
The length is 5 times of width, that is:-
l = 5w = 5(2) = 10
To know more about equation visit:
https://brainly.com/question/1117774
#SPJ1
Help me please I need answers

Answers
Answer:
The solution of the system of equations are;
(-2, -6) and (4, 6)
Step-by-step explanation:
-2·x + y = -2...............(1)
\(y = -\dfrac{1}{2} \cdot x^2 + 3 \cdot x + 2\)........(2)
Equation (1) gives;
y = 2·x - 2
From which we have;
\(2 \cdot x - 2 = -\dfrac{1}{2} \cdot x^2 + 3 \cdot x + 2\)
\(0= -\dfrac{1}{2} \cdot x^2 + x + 4\)
x² -2·x -8 = 0
(x - 4)·(x + 2) = 0
x = 4 or x = -2
The y-coordinate values are;
y = 2×(-2) - 2 = -6 and y = 2×(4) - 2 = 6
The solution points are;
(-2, -6) and (4, 6).
The points where the equation, -2·x + y = -2 and the equation \(y = -\dfrac{1}{2} \cdot x^2 + 3 \cdot x + 2\) intersect are (-2, -6) and (4, 6).

Scatter plots
Group of answer choices
1. are not used for revealing patterns.
2. are used to see two numeric variables plotted in comparison
with each other.
3. must lie on straight lines.
4. are used
Answers
The option that correctly describes scatter plots is:
Option 2: are used to see two numeric variables plotted in comparison with each other.
What is the importance of scatter plots?A scatterplot is defined as a type of graph or mathematical graph that uses Cartesian coordinates to show the values of usually two variables in a data set. Additional variables can be displayed if the points are coded
Scatterplots are used to identify possible relationships between changes observed in two different sets of variables. It provides a visual and statistical way to test the strength of the relationship between two variables.
Looking at the given options and comparing with the definition of scatter plots above, it is very clear that only option 2 is correct because they are used to see two numeric variables plotted in comparison with each other.
Read more about Scatter Plots at: https://brainly.com/question/6592115
#SPJ4
Complete question is:
Group of answer choices
1. are not used for revealing patterns.
2. are used to see two numeric variables plotted in comparison with each other.
3. must lie on straight lines.
4. are used to see two categorical variables plotted in comparison with each other.
Find the factors of 216 p 3 – 125.
Answers
Step-by-step explanation:
216p³ - 125
p³ = 125 / 216
p = 5/6
»216p³ - 125
»216p³ = 125
»p³ = 125/216
»p = ³√125/³√216
»p = 5/6✅
14129 Marks
***
Hamid has 20 T-shirts.
The information shows the colours of his T-shirts.
7 black
4 dark blue
4 red
1 light blue
2 white
2 grey
Hamid is going to take one of his T-shirts at random.
a) What is the probability that the T-shirt will be grey?
b) What is the probability that the T-shirt will not be red?
c) He takes one of his blue T-shirts at random.
What is the probability that the T-shirt is light blue?
Answers
Hamid is going to take one of his T-shirts at random.
The probability of selecting a light blue T-shirt is \(\frac{1}{4}\) or \(0.25\).
a) To find the probability that the T-shirt will be grey, we need to determine the ratio of grey T-shirts to the total number of T-shirts.
From the given information, we know that Hamid has 2 grey T-shirts out of a total of 20 T-shirts.
Therefore, the probability of selecting a grey T-shirt at random is \(\frac{2}{20}\), which simplifies to \(\frac{1}{10}\) or \(0.1\).
b) To find the probability that the T-shirt will not be red, we need to determine the ratio of non-red T-shirts to the total number of T-shirts.
Hamid has 4 red T-shirts, so the number of non-red T-shirts is
\(20 - 4 = 16\).
Therefore, the probability of selecting a T-shirt that is not red is \(\frac{16}{20}\), which simplifies to \(\frac{4}{5}\) or \(0.8\).
c) If Hamid takes one of his blue T-shirts at random, we need to consider the ratio of blue T-shirts to the total number of T-shirts.
From the information provided, we know that Hamid has a total of 4 blue T-shirts.
Therefore, the probability of selecting a blue T-shirt at random is \(\frac{4}{20}\), which simplifies to \(\frac{1}{5}\) or \(0.2\).
d) If Hamid takes one of his blue T-shirts at random, the probability that the T-shirt is light blue depends on the ratio of light blue T-shirts to the total number of blue T-shirts.
From the information provided, there is only 1 light blue T-shirt and a total of 4 blue T-shirts.
Hence, the probability of selecting a light blue T-shirt is \(\frac{1}{4}\) or \(0.25\).
For such more questions on probability
https://brainly.com/question/30390037
#SPJ8
Read this passage from the U.S. Constitution:
I need help please do

Answers
Answer:
the answer is D i believe
please show your work.

Answers
The results for the variable t in each linear equation are listed below:
t = - 1t = - 24t = - 3t = - 2t = - 10How to solve linear equations by algebra properties
In this question we have linear equations with a single variable that must be cleared by using algebra properties. Now we proceed to solve each equation for the variable t:
Equation 1
16 · t + 4 · (5 - t) = 8
16 · t + 20 - 4 · t = 8
12 · t = - 12
t = - 1
Equation 2
18 = 2 · t - 3 · (t + 2)
18 = 2 · t - 3 · t - 6
24 = - t
t = - 24
Equation 3
- 10 · t - (t + 5) = 28
- 10 · t - t - 5 = 28
- 11 · t = 33
t = - 3
Equation 4
- 6 · (3 · t + 5) = 6
- 18 · t - 30 = 6
- 18 · t = 36
t = - 2
Equation 5
12 = 3 · (t + 14)
12 = 3 · t + 42
3 · t = - 30
t = - 10
To learn more on linear equations: https://brainly.com/question/13738061
#SPJ1
it costs 13.50 to rent a canoe and $6 to use the canoe for an hour. You have 37.50. write an equation that represents the number h of hours you can rent the canoe
Answers
Let the number of hours = h
Multiply the rate per hour by hours and add to the rental fee.
This at most can equal the amount you have.
Equation: 6h+ 13.50 <= 37.50
Solve for h:
6h + 13.50 <= 37.50
Subtract 13.50 from both sides:
6h <= 24.00
Divide both sides by 6:
H <= 4
You can rent the canoe for 4 hours maximum.
in analysis of variance, what is measured by the ms values? group of answer choices population variance. the average distance from one mean to another. the total variability for the set of n scores. sample variance
Answers
In analysis of variance, sample variance is measured by an MS value.
The variability in a particular sample is determined using sample variance. A sample is a collection of observations taken from a population that can accurately reflect the entire population. The sample variance is calculated in relation to the data set mean. Additionally called the estimated variance.
Due to the fact that data can be grouped or ungrouped, there are two formulas available to determine the sample variance. The sample standard deviation is also produced by taking the square root of the sample variance. The spread of the data points in a particular data set around the mean is measured using sample variance.
To learn more about sample variance here:
https://brainly.com/question/13708253
#SPJ4
How can you apply mathematical concepts in a natural disaster?
Answers
Answer:
If there was a flood, you would calulate how high the water is.
If g(1) = 2,|g(5) = -6,| and Integral_1^5 g(x) dx = -5,| evaluate the integral Integral_1^5 xg'(x) dx.
Answers
By evaluating the integral \(\int_1^5 xg'(x) dx\) we will get -27.
Given that g(1) = 2, g(5) = -6, and \(\int_1^5 g(x) dx = -5\)
Given integral \(\int_1^5 g(x) dx\) = -5⇒ \(\int_1^5 g(x) dx\) = -5------(1)
∫x g'(x) dx = x g(x) - ∫g(x) dx
As function g(x) is not given, we need to use the above formula to find the \(\int_1^5 xg'(x) dx\).
\(\int_1^5 xg'(x) dx = [x g(x)]_1^5 - \int_1^5 g(x) dx\)
We know that for function g(x), g(1) = 2 and g(5) = -6, so:
\([xg(x)]_1^5 = 5g(5) - 1g(1) = 5(-6) - 2 = -32\)
And we also know that \(\int_1^5 g(x) dx = -5\), so:
\(\int_1^5 xg'(x) dx = [xg(x)]_1^5 - \int_1^5 g(x) dx\)
= -32 - (-5)
= -27
Therefore, \(\int_1^5 xg'(x) dx\) is equal to -27.
To know more about integral: https://brainly.com/question/22008756
#SPJ11
Find the slope that passes through the points (19,-2) and. (11, 10)

Answers
Answer:
12 over -8
Step-by-step explanation:
In this diagram, ABAC – AEDF. If the
area of ABAC = 15 in2, what is the
area of AEDF?
D
E
4 in
F
B
5 in
Area = [?] in
Enter a decimal rounded to the tenths,
1
Plz help ive been on this for 2 hours.
![In this diagram, ABAC AEDF. If thearea of ABAC = 15 in2, what is thearea of AEDF?DE4 inFB5 inArea = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/OI9civCAFmTvnySIvc5TbUUNNQwOOkVT.png)
Answers
Answer:
48/5in2=9.6in2 ~ 10in2
![In this diagram, ABAC AEDF. If thearea of ABAC = 15 in2, what is thearea of AEDF?DE4 inFB5 inArea = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/7iiw5D5TqbJjK6QTo6MYQ7qQjhI3Yp4o.jpeg)
HELLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLPPPPPPPPPPPPPPPPP
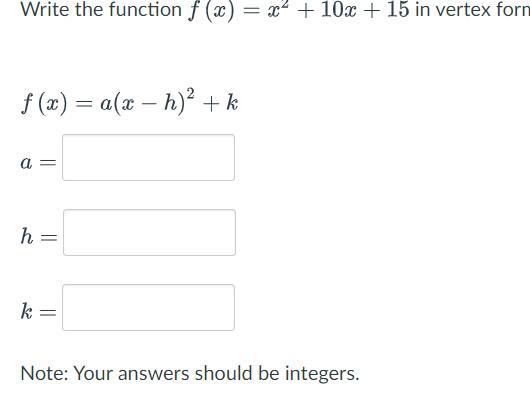
Answers
Answer:
a, h and k have values 1, -5 and -10 respectively

Given a circle centered at point O and an arbitrary point P, consider the locus of all points Y that occur as midpoints of segments PX, where X lies on the given circle. Show that this locus is a circle with radius half of the original circle. Locate the center of the locus
Answers
the focus of all points Y that occur as midpoints of segments PX, where X lies on the given circle, is a circle with radius half of the original circle (R/2) and its center located at the midpoint M of segment OP.
Given a circle centered at point O and an arbitrary point P, let's consider the focus of all points Y that occur as midpoints of segments PX, where X lies on the given circle.
To show that this focus is a circle with radius half of the original circle, let's first analyze the properties of the midpoint Y. By definition, Y is the midpoint of segment PX, so PY = YX.
Let the radius of the original circle be R, and let OP = d. Using the law of cosines, we can derive the distance between X and P as follows:
PX² = OP² + OX² - 2(OP)(OX)cos∠POX.
Since OX = R, OP = d, and ∠POX = θ, we have:
PX² = d² + R² - 2dRcosθ.
Now, let's consider the distance between Y and P. Since Y is the midpoint of segment PX, we have:
PY² = (1/2PX)² = (1/4)(d² + R² - 2dRcosθ).
Now, let's find the locus of Y. To do so, we will fix the distance PY and let the angle θ vary. The locus of Y will be the set of all points equidistant from P with distance (1/2)PX. This forms a circle centered at a point M with radius half of the original circle (R/2).
To locate the center M of the locus, let's consider the midpoint of segment OP. Since Y lies on the line segment PX, and Y is the midpoint of PX, the locus of Y will be the set of all points equidistant from the midpoint of segment OP. This forms a circle centered at point M, where M is the midpoint of segment OP.
To learn more about circle click here
brainly.com/question/29142813
#SPJ11
In the following problems, solve the given initial-value problem. y′′+16y=0, y(0)=2,y′(0)=−2 y′′+y′+2y=0, y(0)=y′(0)=0
Answers
1) The solution to the initial-value problem is y(t) = 2 cos(4t) - (1/2) sin(4t).
2) The solution to the initial-value problem is y(t) = 0.
Let's solve the initial-value problems given.
Initial-Value Problem: y'' + 16y = 0, y(0) = 2, y'(0) = -2
We have a second-order linear homogeneous differential equation. To solve this, we assume a solution of the form y(t) = \(e^{rt\), where r is a constant to be determined.
Substituting this assumed solution into the differential equation, we get the characteristic equation:
\(r^2\) + 16 = 0
Solving the characteristic equation for r, we have:
r = ±4i
Since the roots are complex (r = 4i and r = -4i), the general solution will involve complex exponentials.
The general solution for the differential equation is:
y(t) = \(c_1\) cos(4t) + \(c_2\) sin(4t)
To find the particular solution that satisfies the initial conditions, we substitute the initial conditions y(0) = 2 and y'(0) = -2 into the general solution:
y(0) = \(c_1\) cos(0) + \(c_2\) sin(0) = \(c_1\) = 2
y'(0) = -4\(c_1\) sin(0) + 4\(c_2\) cos(0) = 4\(c_2\) = -2
Solving these equations, we find \(c_1\) = 2 and \(c_2\) = -1/2.
Therefore, the solution to the initial-value problem is:
y(t) = 2 cos(4t) - (1/2) sin(4t)
2) Initial-Value Problem: y'' + y' + 2y = 0, y(0) = y'(0) = 0
We have a second-order linear homogeneous differential equation. To solve this, we assume a solution of the form y(t) = \(e^{rt\), where r is a constant to be determined.
Substituting this assumed solution into the differential equation, we get the characteristic equation:
\(r^2\) + r + 2 = 0
Solving the characteristic equation for r, we have:
r = (-1 ± √(1 - 4(1)(2)))/2
= (-1 ± √(-7))/2
= (-1 ± i√7)/2
Since the roots are complex, the general solution will involve complex exponentials.
The general solution for the differential equation is:
y(t) = \(c_1\) \(e^{-t/2\) cos((√7/2)t) + \(c_2\) \(e^{-t/2\) sin((√7/2)t)
To find the particular solution that satisfies the initial conditions, we substitute the initial conditions y(0) = 0 and y'(0) = 0 into the general solution:
y(0) = \(c_1\) = 0
y'(0) = -(1/2)\(c_1\) + (√7/2)\(c_2\) = 0
Solving this equation, we find \(c_1\) = 0 and \(c_2\) = 0.
Therefore, the solution to the initial-value problem is:
y(t) = 0
In this case, the zero solution satisfies the initial conditions.
To learn more about initial-value here:
https://brainly.com/question/30503609
#SPJ4
637,982 + 2,819 i need it
Answers
Answer: 640801
Step-by-step explanation: Simply add both together, 637,982 plus 2819.
Answer:
637, 982 + 2,819 = 640,801
Create a triangle of your choice on the grid. Measure the lengths of all the sides on the triangle and record them in the table.
Answers
Step-by-step explanation:
The program I used tells me the lengths, though I could use the law of cosines or Pythagoras's Therom for this.
AB: 2
BC: 3
AC: About 3.61
Also, point A is (-2, 4), point B is (-2, 2), and point C is (1, 2)
Hope this helps!

We have the partial equilibrium model below for a market where there is an excise tax , f
Q d =Q s
Q d =a 1 +b 1 P
Q s =a 2 +b 2 (P−t)
where Q is quantity demanded, Q, is quantity supplied and P is the price. Write down the model on the form Ax=d and use Cramer's rule to solve for Q s∗ and P ∗ .
Answers
We can write the given partial equilibrium model on the form Ax = d, and then use Cramer's rule to solve for the values of Qs* and P*.
To write the model on the form Ax = d, we need to express the equations in a matrix form.
The given equations are:
Qd = a1 + b1P
Qs = a2 + b2(P - t)
We can rewrite these equations as:
-Qd + 0P + Qs = a1
0Qd - b2P + Qs = a2 - b2t
Now, we can represent the coefficients of the variables and the constants in matrix form:
| -1 0 1 | | Qd | | a1 |
| 0 -b2 1 | * | P | = | a2 - b2t |
| 0 1 0 | | Qs | | 0 |
Let's denote the coefficient matrix as A, the variable matrix as x, and the constant matrix as d. So, we have:
A * x = d
Using Cramer's rule, we can solve for the variables Qs* and P*:
Qs* = | A_qs* | / | A |
P* = | A_p* | / | A |
where A_qs* is the matrix obtained by replacing the Qs column in A with d, and A_p* is the matrix obtained by replacing the P column in A with d.
By calculating the determinants, we can find the values of Qs* and P*.
It's important to note that Cramer's rule allows us to solve for the variables in this system of equations. However, the applicability of Cramer's rule depends on the properties of the coefficient matrix A, specifically its determinant. If the determinant is zero, Cramer's rule cannot be used. In such cases, alternative methods like substitution or elimination may be required to solve the equations.
Learn more about matrix here:
https://brainly.com/question/29132693
#SPJ11
13-18 plz help me find the measure of each angle indicated. then state the type of angle pair
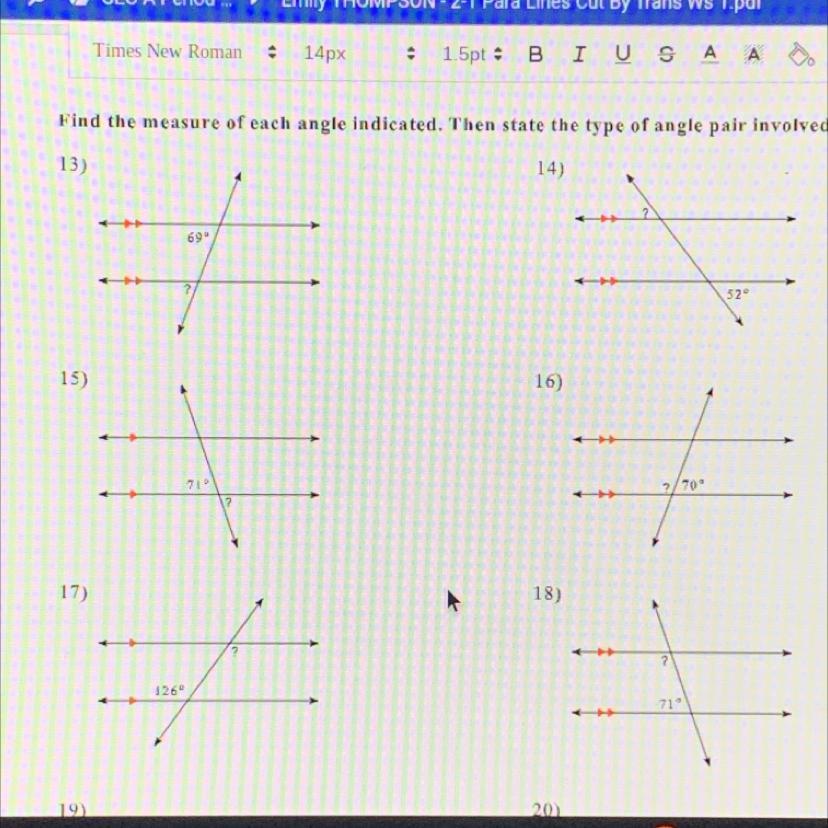
Answers
Answer:
13)69°{corresponding angles}
14)52°{exterior alternate angles}
15)71°{vertically opposite angle}
16)110°{supplementary angles}
17)126°{interior alternate angles}
18)109°{co interior}
13. 69*
14. 52*
15. 71*
16. 110*
17. 126*
18. 109*
What is the tangent ratio of angle BCD?
A) 10√3 over 20
B) 10√3 over 10
C) 10 over 10√3
D) 10 over 20√3

Answers
Answer:
B)
Step-by-step explanation:
given the 2 angles of 60°, that makes the 3rd angles also 60° (remember, the sum of all angles in a triangle is always 180°).
and that makes the triangle an equilateral triangle (all 3 sides are equally long : 20).
BD = sin(60)×20
CD = cos(60)×20
tan(60) = sin(60)/cos(60) = sin(60)×20/(cos(60)×20)
CD = 20/2 = 10
for BD we need Pythagoras
20² = BD² + 10²
400 = BD² + 100
300 = BD²
BD = sqrt(300) = sqrt(4×75) = sqrt(4×25×3) =
= 2×5×sqrt(3) = 10×sqrt(3)
so,
tan(60) = BD/CD = 10×sqrt(3) / 10
which is sqrt(3), by the way.
Simplify 3n+2(-2n-1)
Answers
Answer:
-n-2
Step-by-step explanation:
The half price of helium-5 is 7.6 X 10 to the power of negative 22 seconds and the half-life helium -9 is 7 x 10 to the power of negative 21-second approximately how many times greater is the half life of helium and -9 then that of helium -5
Answers
Answer:
Approximately 9.211 times
Step-by-step explanation:
Given
\(x = 7.6 * 10^{-22}s\) --- half life of helium-5
\(y = 7 * 10^{-21}s\) --- half life of helium-9
Required
How many times greater is y than x
To do this, we simply divide y by x
\(\frac{y}{x} = \frac{7 * 10^{-21}s}{7.6 * 10^{-22}s}\)
\(\frac{y}{x} = \frac{7 * 10^{-21}}{7.6 * 10^{-22}}\)
Apply law of indices
\(\frac{y}{x} = \frac{7 * 10^{-21--22}}{7.6}\)
\(\frac{y}{x} = \frac{7 * 10^{-21+22}}{7.6}\)
\(\frac{y}{x} = \frac{7 * 10}{7.6}\)
\(\frac{y}{x} = \frac{70}{7.6}\)
\(\frac{y}{x} = 9.211\)
Evaluate 3x + 1 when x = 2.
A. 5
B. 6
C. 7
Answers
Answer:
The correct answer:
C. 7
3(2) + 1 = 6 + 1 = 7
Step-by-step explanation:
So the question is 3x+1. We are given the information that x=2. Therefor we would plug in 2 to where x is. 3(2)+1. Now we would multiply first for 6+1. Add to get 7. 7 would be our answer giving us C.
a sociologist interested in salesperson-consumer interaction wanted to know if customers really are influenced to buy more from sales clerks who smile. to test this, clerks at eight stores in a large canadian clothing chain were given special instructions at the start of a week, and the number of sales over the week were recorded. four of the stores were randomly selected to have the clerks receive instructions to be especially courteous and to smile a lot. clerks at four other stores were simply instructed to be especially courteous. sales (in thousands of dollars) for the four stores in the smile condition were 36, 40, 36, and 44; sales for the four stores in the control condition were 40, 31, 27, and 30. do these results suggest that customers might buy more if they encounter smiling sales clerks? (use the .05 level.)
Answers
The results indicate that encountering sales clerks who smile could potentially increase customer purchases.
How to determine the statementFrom the information given, we have that;
The four stores in the smile condition were 36, 40, 36, and 44;
To determine the t-value, we need to first calculate the mean for the control condition, we have;
Mean = 36 + 40 + 36+ 44/4
Mean =126/4
Mean = 32
Mean for the smile condition;
Mean = 39
One can employ a t-test to compare the average values of the two situations in order to scrutinize the outcomes. With a significance level of 0. 05, a two-tailed test with six degrees of freedom would require a critical t-value of around 2. 447
Learn more about t-value at: https://brainly.com/question/31687253
#SPJ1
FILL IN THE BLANK. A good way to get a small standard error is to use a ________.1. Large sample2. Large population3. Repeated sampling4. Small sample5. Small population
Answers
A good way to get a small standard error is to use a Large sample. the correct answer is option 1.
The standard error is a measure of the variability of the sampling distribution of a statistic. A smaller standard error indicates that the statistic is more precise and is likely closer to the true population value.
One way to obtain a smaller standard error is to use a larger sample size. This is because a larger sample size tends to produce a more accurate estimate of the population parameter, with less variability. Therefore, option 1, "Large sample," is the correct answer.
The other options, such as a large population, repeated sampling, small sample, or small population, are not necessarily related to obtaining a small standard error.
To learn more about standard error click on,
https://brainly.com/question/13179711
#SPJ11