Shawna is saving money to buy a new laptop. She starts her savings with $64. Each week, she adds another $17 to her savings. Graph the relationship that models the amount of money Shawna is saving. If her laptop costs $589, after how many weeks will she be able to afford the laptop?
Answers
Answer:
4 weeks
Step-by-step explanation:
Related Questions
Given the following discrete noise signal: [0.031, 0.073, 0.047, 0.06, 0.056, 0.042, 0.012, 0.041, 0.081, 0.072], calculate the standard deviation and RMS of the noise
Answers
Therefore, the standard deviation of the noise is approximately 0.0372, and the RMS of the noise is approximately 0.0584.
To calculate the standard deviation and RMS (Root Mean Square) of the given discrete noise signal [0.031, 0.073, 0.047, 0.06, 0.056, 0.042, 0.012, 0.041, 0.081, 0.072], follow these steps:
Step 1: Calculate the mean (average) of the data:
Mean = (0.031 + 0.073 + 0.047 + 0.06 + 0.056 + 0.042 + 0.012 + 0.041 + 0.081 + 0.072) / 10
= 0.055
Step 2: Calculate the variance of the data:
Variance\(= [(0.031 - 0.055)^2 + (0.073 - 0.055)^2 + (0.047 - 0.055)^2 + (0.06 - 0.055)^2 + (0.056 - 0.055)^2 + (0.042 - 0.055)^2 + (0.012 - 0.055)^2 + (0.041 - 0.055)^2 + (0.081 - 0.055)^2 + (0.072 - 0.055)^2] / 10\)
= 0.00138
Step 3: Calculate the standard deviation:
Standard Deviation = √(Variance)
= √(0.00138)
≈ 0.0372 (rounded to four decimal places)
Step 4: Calculate the RMS (Root Mean Square):
RMS = √\(((0.031^2 + 0.073^2 + 0.047^2 + 0.06^2 + 0.056^2 + 0.042^2 + 0.012^2 + 0.041^2 + 0.081^2 + 0.072^2) / 10)\)
= √(0.0034)
≈ 0.0584 (rounded to four decimal places)
To know more about standard deviation,
https://brainly.com/question/14896796
#SPJ11
Eric's city took a telephone poll about a plan to build a new hotel downtown. 200 people took
the poll. 25% of them were in favor of the new hotel. How many people were in favor of the
new hotel?
Answers
Answer:
50 people
Step-by-step explanation:
Solution
25% as a fraction is 25/100 which reduces down to 1/4. What this tells you is that 1/4 of the people asked want the hotel
1/4 * 200 = 50
50 people want the hotel.
for each of the following, show that the differential form is not exact, but becomes exact when multiplied through by the given integrating factor
Answers
To determine if a differential form is exact, we need to check if its partial derivatives satisfy the condition of equality. If the differential form is not exact, we can multiply it by an integrating factor to make it exact.
Given a differential form of the form M(x, y)dx + N(x, y)dy, we can determine if it is exact by checking if ∂M/∂y = ∂N/∂x. If this condition is not satisfied, the differential form is not exact. However, we can multiply the differential form by an integrating factor to make it exact.
By multiplying the original differential form by an integrating factor, which is usually a function of either x or y, the resulting form will have equal partial derivatives, satisfying the condition for exactness. The integrating factor effectively "corrects" the form and makes it exact.
By finding the appropriate integrating factor and multiplying it with the given differential form, we can transform it into an exact form. This process is a fundamental technique in solving certain types of differential equations and allows us to find solutions that would otherwise be challenging to obtain.
To learn more about partial derivatives click here : brainly.com/question/28750217
#SPJ11
The First Integral Is From 0 To 1, The Second Is From 0 To Y, The Third Is From 0 To Sqrt(1-X2). Try To Show SKETCH!!
Answers
Given integrals are,∫[0 to 1]∫[0 to y]∫[0 to √(1 - x²)] f(x, y, z) dzdxdy
Hence, we can sketch the given integral as follows:
As we have given 3 integral expressions that are dependent on one another.
Therefore, to solve this problem, we will start with the innermost integral.
The first integral is ∫[0 to √(1 - x²)] f(x, y, z) dz, and the limits are from 0 to the value of √(1 - x²).
When we solve the first integral, we get,∫[0 to 1]∫[0 to y] [∫[0 to √(1 - x²)] f(x, y, z) dz] dxdy Next, we need to solve the second integral that is dependent on the first integral.
Therefore, the second integral is,∫[0 to y] [∫[0 to √(1 - x²)] f(x, y, z) dz] dxAnd, the limits of the second integral are from 0 to y.
We can now write the final integral expression as,∫[0 to 1]∫[0 to y] [∫[0 to √(1 - x²)] f(x, y, z) dz] dxdy.
To know more about integrals visit:
brainly.com/question/32562155
#SPJ11
A line of symmetry divides a figure into two equal halves in all aspects. State true or false.
Answers
The statement A line of symmetry divides a figure into two equal halves in all aspects is true.
A line of symmetry does indeed divide a figure into two equal halves in all aspects. When a figure has a line of symmetry, it means that if you were to fold the figure along that line, both halves would match exactly. This implies that the two halves of the figure are mirror images of each other, and they are congruent in terms of shape, size, and all other aspects.
The concept of symmetry is widely used in various fields, including mathematics, art, and design. Figures that possess symmetry often have an aesthetically pleasing and harmonious appearance.
To learn more about symmetry
https://brainly.com/question/12296313
#SPJ11
Find the x and y intercept of y=0.5x^2-3x.
Answers
Step-by-step explanation:
i don't have a step by step explanation so here you go the answer

(−6d+6)(2d−2)=
Ill give a brainliest
Answers
Answer:
This is what I found from google

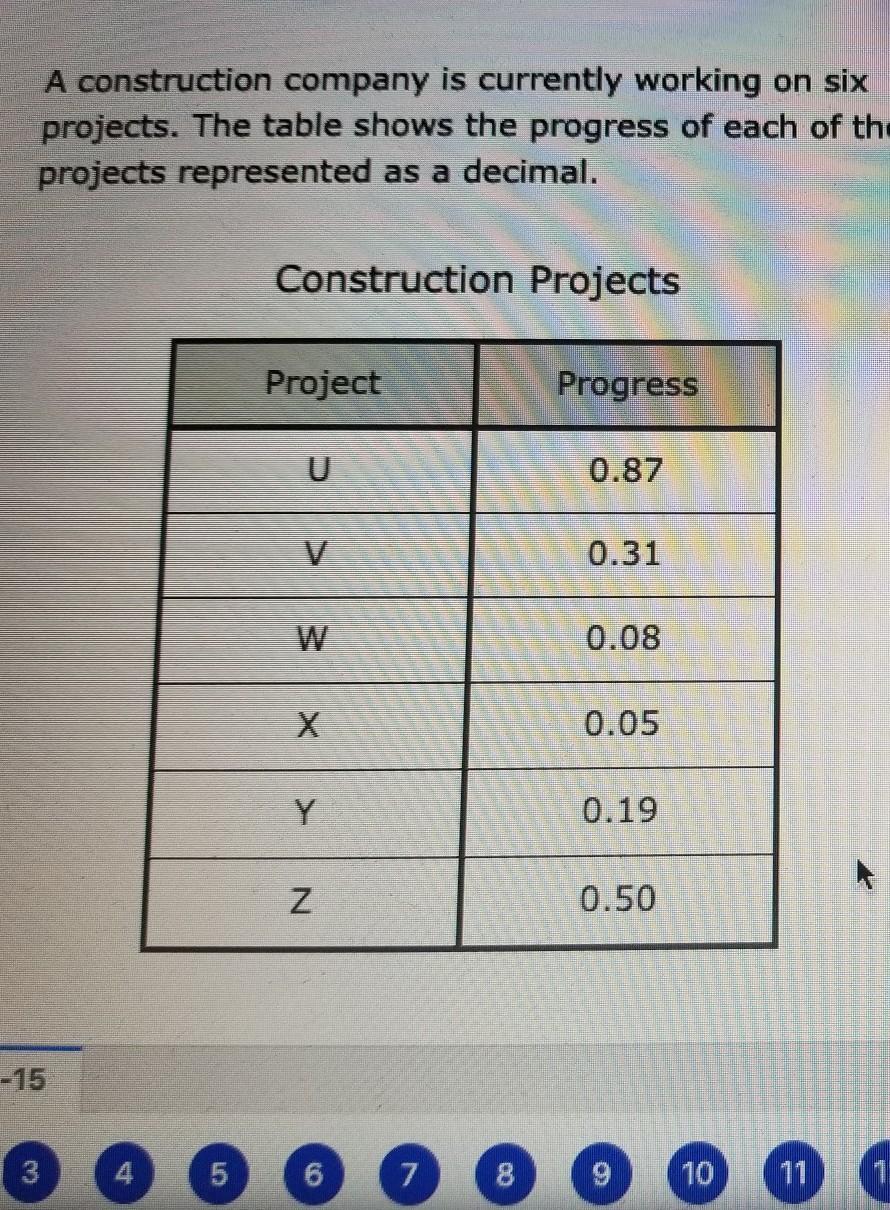
A construction company is curretly working on six projects the table shows the progress of each of the projrcts represented as a decimal what Is the range of the progrese of these projects
Answers
The range of the progress of the construction company's six projects is 0.82.
The range of data is a measure of its spread. To calculate the range, you subtract the smallest value from the largest value.
The data for this problem is:
Project Progress
u 0.87
v 0.31
w 0.08
x 0.05
y 0.19
z 0.5
In this case, the smallest value is 0.05 (project x) and the largest value is 0.87 (project u), so:
= 0.87 - 0.05 = 0.82This means that the difference between the most advanced project and the least advanced project is 0.82. The range is an important measure of variability and helps in understanding the distribution of data, in this case, the progress of the construction projects.
Learn more about range in statistics brainly.com/question/8486248
#SPJ4
A triangle has side lengths measuring 20 cm, 5 cm, and n cm. Which describes the possible values of n?
O 5
O 5
O 15
O 15
Answers
There are three sticks: A, B and C. The length of stick A is 82% of the length of stick B. The length of stick B is 60% the length of stick C. If B is 270 cm long, how many centimeters is A and C?
Answers
Answer:
A:221.4 cm
C:450 cm
Step-by-step explanation:
For A we do B multiple by 82% which is 270 multiple by 0.82
for C we do 270 over 60% which is 270/0.6
one important point to remember is that just because a difference between two treatment groups is found to be statistically significant, it does not mean that the difference:
Answers
Researchers use a finding's Effect size to measure magnitude and reliability.
a difference in significance does not always make a significant difference.
One reason is the arbitrary nature of the p<0.05 cutoff. We could get two very similar results, with p=0.04 and p=0.06, and mistakenly say they’re clearly different from each other simply because they fall on opposite sides of the cutoff.
The second reason is that p values are not measures of effect size, so similar p values do not always mean similar effects. Two results with identical statistical significance can nonetheless contradict each other.
Effect size refers to the measure of the magnitude of the experiment's effect. In other words, effect size measures how important is the relationship between two variables. The larger the effect size, the stronger this relationship is. Moreover, when the effect size is large, you are more likely to be dealing with a relationship that has practical significance.
For more information on statistical significance click on the link below:
https://brainly.com/question/13278721
#SPJ4
Whats 1+1+2+3+7+4+9=?
Answers
Answer:
27
thanks for the points
Find the equation of the line perpendicular to \(-\frac{1}{2} x\) and passing through the point (−6; 1).
Answers
Y-1=2(x+6)
Y=2x+13 is the answer
⦿ Hi There! ⦿
Point-Slope form:
y-y1=m(x-x1)
y-1=m(x-(-6)
Perpendicular lines have slopes that are opposite reciprocals.
It means that if we have -1/2, we flop it over and make it positive.
So the slope of the new line is 2.
y-y1=m(x-x1)
y-1=2(x-(-6)
y-1=2(x+6)
y=1=2x+12
y=2x+12-1
y=2x+11
Hope it helps!
~Just a cheerful gal
#CarryOnLearning
Answered by
\(-SilentNature-\)
a washer and dryer cost a total of $936. The cost of the washer is two times the cost of the dryer. find the cost of each item
Answers
Step-by-step explanation:
The washer costs $624 and the dryer costs 312.
624 is double 312 so that works out. Also if you add 624 and 312 you get 936.
Answer:
Washer = 642
Dryer = 321
Step-by-step explanation:
please help will give brainliest please no links I rlly need this
A) Find the probability that a point chosen randomly inside the rectangle will be in the triangle. Show all calculations. Round answer to the nearest hundred
B) Find the probability that a point chosen randomly inside the rectangle will be in the shaded region. Show all calculations. Round answer to the nearest hundredth. Answer:

Answers
Step-by-step explanation:
1st,
the area of the rectangular =7×5=35
area of triangle =3×4/2=6
area of square =2×2=4
area of shadowed region =35-(6+10)=25
According to the question,
A) Find the probability that a point chosen randomly inside the rectangle will be in the triangle. Show all calculations. Round answer to the nearest hundred
answer:-
probability of a point in rectangle inside triangle =6/35=0.17
B) Find the probability that a point chosen randomly inside the rectangle will be in the shaded region. Show all calculations. Round answer to the nearest hundredth.
answer:
probability of that a point chosen randomly inside the rectangle will be in the shaded region=25/35=5/7=0.71
Given: DF¯¯¯¯¯¯¯≅GH¯¯¯¯¯¯¯¯
; ∠F
and ∠H
are right angles.
Drag the missing statement to the box to prove that △DEF≅△GEH.


Answers
So ∠DFE≅ ∠GHE, the missing letter is E. To prove use ASA Congruence Theorem.
What do you mean by ASA Congruence?ASA congruence is a geometric congruence between two triangles that states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. The acronym ASA stands for "angle-side-angle."
∠DFE≅∠GHE; ∠F and ∠H are right angles. To prove that △DEF≅△GEH, we can use the statement: "If two angles of one triangle are congruent to two angles of another triangle, and the included side of one triangle is congruent to the included side of the other triangle, then the two triangles are congruent." This statement is known as the ASA Congruence Theorem.
To know more about triangle visit:
https://brainly.com/question/13263113
#SPJ1
What is the forecast for May using a five-month moving average?(Round answer to the nearest whole number.) Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47
A. 43 B. 47 C. 52 D. 38 E. 39
Answers
The forecast for May using a five-month moving average is 39 (Option E).
Moving average is used for smoothing out time series data to find any trends or cycles within the data. A five-month moving average is the average of the past five months. To calculate the moving average, add up the sales for the previous five months and divide it by five.
According to the question, the sales for the previous five months are: Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47
We have to add the sales of these five months, which gives:
27 + 40 + 42 + 41 + 47 = 197
To find the moving average for May, we divide this sum by 5:
197 / 5 = 39.4
Since we have to round the answer to the nearest whole number, we round 39.4 to 39, which is option E.
Learn more about Moving average here: https://brainly.com/question/28495879
#SPJ11
If the rental skis at Mt Buller were lined up end to end, they would reach from the summit of Mt Buller all the way down to the entry gate at Mirimbah. The average length of a downhill ski is 1.5 m and the distance from the Mt Buller summit to Mirimbah is 18.3km . How many rental skis are there?
Answers
Answer:
There are 12,200 rental skis
Step-by-step explanation:
The distance the rental skis would reach if they were lined up end to end = From Mt Buller summit to Mirimbah
The average length of each downhill ski, l = 1.5 m/ski
The distance from Mt Buller summit to Mirimbah, D = 18.3 km = 18,300 m
The number of rental skis at Mt Buller, n = D/l
∴ n = 18,300 m/(1.5 m/ski) = 12,200 skis
The number of rental skis at Mt Buller, n = 12,200 skis
(We have that there are two skis per pair, therefore, the number of pairs of skis at Mt Buller = 12,200 ski/2 = 6,100 pairs of skis)
(x+4) ² remove bracket and simplify
Answers
Answer:
To expand (x + 4)², we can use the formula for squaring a binomial: (a + b)² = a² + 2ab + b². In this case, a = x and b = 4.
So,
(x + 4)² = x² + 2(x)(4) + 4²
= x² + 8x + 16
Thus, (x+4)² when expanded and simplified gives x² + 8x + 16.
Step-by-step explanation:
Answer:
x²n+ 8x + 16
Step-by-step explanation:
(x + 4)²
= (x + 4)(x + 4)
each term in the second factor is multiplied by each term in the first factor, that is
x(x + 4) + 4(x + 4) ← distribute parenthesis
= x² + 4x + 4x + 16 ← collect like terms
= x² + 8x + 16
What are independent variables and dependent variables when
conducting a research design to investigate the impact of a school
nutrition program on grade performance of students at high
school?
Answers
Independent variables are the factors that are manipulated or controlled by the researcher in a study. In the context of investigating the impact of a school nutrition program on grade performance of high school students, the independent variable would be the school nutrition program itself.
The researcher would design and implement the program, and this variable would be under their control.
Dependent variables, on the other hand, are the outcomes or variables that are measured in a study and are expected to change as a result of the independent variable. In this case, the dependent variable would be the grade performance of the students. The researcher would collect data on the grades of the students before and after the implementation of the nutrition program, and this would be the variable that is expected to be influenced by the independent variable.
In summary, the independent variable in this research design is the school nutrition program, while the dependent variable is the grade performance of the students. The researcher would manipulate the independent variable (implement the nutrition program) and then measure the dependent variable (student grades) to determine if there is an impact of the program on grade performance.
Learn more about Independent variables here:-
https://brainly.com/question/32711473
#SPJ11
Find the product. ( 5 6 ) ( 1 7 ) = (5)(1) (6)(7)
Answers
The product of the matrices ( 5 6 ) and ( 1 7 ) is equal to 47.
The number of columns in the first matrix must equal the number of rows in the second matrix in order for two matrices to be multiplied. In this instance, the 1x2 multiplied by 2x1 matrix satisfies this requirement.
In many disciplines, such as computer graphics, physics, and engineering, matrix multiplication is a key idea in linear algebra. It can be used to transform data, determine eigenvalues and eigenvectors, and solve systems of linear equations.
To get the product of two matrices, we need to perform the dot product of each row in the first matrix with each column in the second matrix.
Given the matrices ( 5 6 ) and ( 1 7 ), we can perform the dot product as follows:
( 5 6 ) ( 1 7 ) = ( (5)(1) + (6)(7) )
= (5 + 42)
= 47
Learn more about product here:
https://brainly.com/question/30284183
#SPJ4
Help this is i-ready!
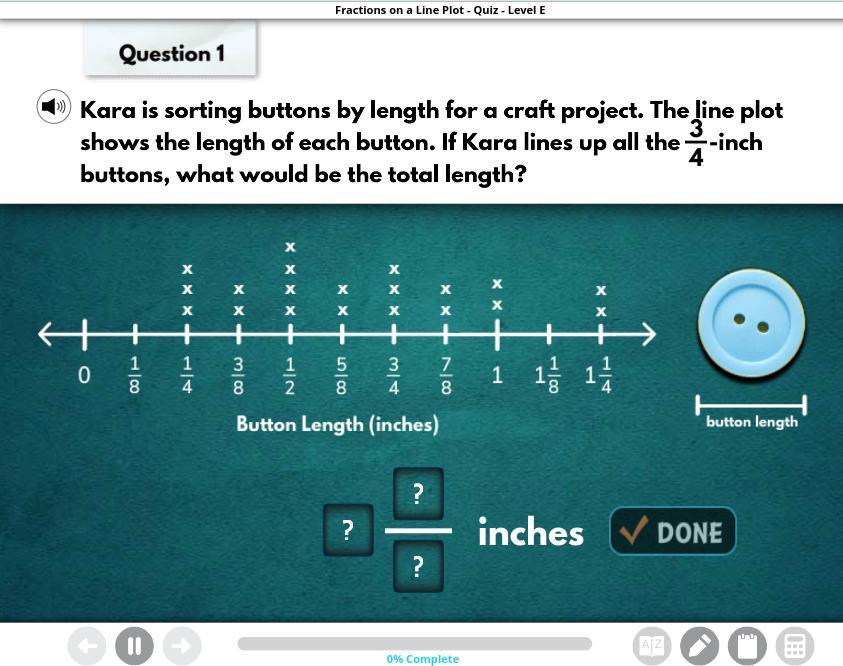
Answers
Answer:
I think the answer is 2 1/4. srry if I'm wrong tho
Answer:
2 1/4 inches
Step-by-step explanation:
Since there are 3 buttons that are 3/4 inch. You will multiply 3/4 and 3.
\(\frac{3}{4}\) × \(\frac{3}{1}\) = \(\frac{9}{4}\)
Change to a mixed number by dividing 9 by 4. You will get 2 1/4 inches.
what is 90.90 rounded to the ones
Answers
Answer:
91.00
Step-by-step explanation:
I got you
a rectangle has a perimeter of 128 inches. the length is four less than twice the width. what is the length of the rectangle?
Answers
The length of the rectangle is approximately 41.34 inches.
Let's assume the width of the rectangle is represented by the variable w. According to the given information, the length of the rectangle is four less than twice the width, which can be expressed as 2w - 4.
The perimeter of a rectangle is calculated by adding the lengths of all four sides. In this case, the perimeter is given as 128 inches. Since a rectangle has two pairs of equal sides, we can set up the equation:
2w + 2(2w - 4) = 128.
Simplifying the equation, we get:
2w + 4w - 8 = 128,
6w - 8 = 128,
6w = 136,
w = 22.67.
So, the width of the rectangle is approximately 22.67 inches. To find the length, we can substitute this value back into the expression 2w - 4:
2(22.67) - 4 = 41.34.
Therefore, the length of the rectangle is approximately 41.34 inches.
In summary, the length of the rectangle is approximately 41.34 inches. This is determined by setting up a system of equations based on the given information: the perimeter of the rectangle being 128 inches and the length being four less than twice the width.
By solving the system of equations, we find that the width is approximately 22.67 inches, and substituting this value back, we obtain the length of approximately 41.34 inches.
To know more about length refer here:
https://brainly.com/question/2497593
#SPJ11
A map scale is 2 in : 15 mi. Two cities are 5.7 in. apart on the map. Find the actual distance between the two cities. Enter the number only.
Answers
Answer:
70!km is the right answer
Step-by-step explanation:
The distance between two cities on a map is 3.5 centimeters. the map is uses a scale in which 1 centimeters represents 20 kilometers.
The average height of American women (in 2016) is 5 ft. 4 inches (64 inches) with a standard deviation of 3 inches. What is the probability that the average height of a random group of nine American women would be less than five feet three inches
Answers
Probability of average height of women is 0.1379
First check to see if the Central Limit Theorem applies. Since n > 30, it does. Next we need to calculate the standard error. To do that we divide the population standard deviation by the square-root of n, which gives us a standard error of 0.646. Next, we calculate a z-score using our z-score formula:
Z=(X−μ)/S.E.
S.E = σn/√n
S.E =3/√ 9
S.E=1
Plugging in gives us:
(64−63)/1 = 1
Finally, we look up our z-score in our z-score table to get a p-value.
The table gives us a p-value of,
P(z<1.0)=1−P(z>1.0)
P(z<1.0)=1−0.8621
P(z<1.0)=0.1379
So, Probability of average height of women is 0.1379
Learn more about PROBABILITY here
https://brainly.com/question/24756209
#SPJ4
rearrange the formula d= m/v for m
Answers
Answer:
m=d*v
Step-by-step explanation:
I genuinely have no idea

Answers
Answer:
10/13/17
15/15/22
Step-by-step explanation:
I may of made some mistakes but I tried, I hope this helps you.
PLEASE HELP ASAP!!!! I NEED HELP, THIS IS DUE IN 15 MINUTES!!!! I’LL GIVE BRAINLIEST!!!!!!
The given table of values shows a linear relationship.
x 1 3 5 7 9
y 8 14 20 26 32
What is the rate of change for this relationship?
Answers
Answer:
Step-by-step explanation:
So sorry because this is due in 15 minutes but if I am calculating this right the rate of change should be 3 since the x goes up by 2 and the y goes up by 6 and the formula is change of y over change of x and it would be 6/2 equaling 3.
Find the H.C.F. of 567 and 255 using Euclid’s division lemma.
Answers
Step-by-step explanation:
To find the Highest Common Factor (H.C.F.) of 567 and 255 using Euclid's division lemma, we can follow these steps:
Step 1: Apply Euclid's division lemma:
Divide the larger number, 567, by the smaller number, 255, and find the remainder.
567 ÷ 255 = 2 remainder 57
Step 2: Apply Euclid's division lemma again:
Now, divide the previous divisor, 255, by the remainder, 57, and find the new remainder.
255 ÷ 57 = 4 remainder 27
Step 3: Repeat the process:
Next, divide the previous divisor, 57, by the remainder, 27, and find the new remainder.
57 ÷ 27 = 2 remainder 3
Step 4: Continue until we obtain a remainder of 0:
Now, divide the previous divisor, 27, by the remainder, 3, and find the new remainder.
27 ÷ 3 = 9 remainder 0
Since we have obtained a remainder of 0, the process ends here.
Step 5: The H.C.F. is the last non-zero remainder:
The H.C.F. of 567 and 255 is the last non-zero remainder obtained in the previous step, which is 3.
Therefore, the H.C.F. of 567 and 255 is 3.