Select the correct answer from each drop-down menu.
Consider absolute value function f.
f(x) = -2/3|x + 4|
The vertex of the function is a(maximum, minimum)
at (0,4) (-4,0) (4,0) (0,-4)
Answers
Step-by-step explanation:
hope you can understand

Related Questions
A square has a diagonal of 15 millimeters. Find its area (nearest tenth).
Answers
Answer:
The answer is 112.5
Step-by-step explanation:
Kams monthly budget includes 249 for food, 160 for gasoline, and 150 for utilities. If he earns 1506 per month after taxes, how much money is left for other expenses ?
Answers
the teacher has a small class with only 7 students. the teacher grades their homework and reports scores of: 10, 7, 8, 12, 9, 11, and 13. what is the median?
Answers
Answer:
10
Step-by-step explanation:
To find the median in a set of data, organize the data from least to greatest.
Here, our data is the homework scores, those being:
10, 7, 8, 12, 9, 11, 13
Let's organize them in ascending order, like so:
7, 8, 9, 10, 11, 12, 13
The next step in finding the median is figuring out which number is in the middle. Since the amount of data we have is an odd number (7), there will be only one number in the middle.
We can find that the number in the middle is 10.
Thus, the median of the scores is 10.
explain how to find the originle and the new dimensions of an object when the scale change
Answers
In general, the origin of the new object is the same because the scalation is made by using the origin of the previous object as a fixed point.
The dimensions of the new object are found simply by multiplying each coordinate of special points of the object by the scale factor.
For example, if the points (x1,y1), (x2,y2) and (x3,y3) are vertices of an object with triangle shape, the new object will have the coordinates
(k*x1,k*y1), (k*x2,k*y2) and (k*x3,k*y3) where the scale factor is k.
do the following by paper folding using a circular cut out.
make the diameter
shade the minor and major segment
make a sector of a circle
Answers
The shaded region of segments is given in the attachment.
What is Circle?A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre.
The diameter is the length of the line through the center that touches two points on the edge of the circle.
A segment of a circle can be defined as a region bounded by a chord and a corresponding arc lying between the chord's endpoints.
A sector of a circle is a pie-shaped part of a circle made of the arc along with its two radii.
Hence, the shaded region of segments is given in the attachment.
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ1


Anyone know how to do this?

Answers
From the given figure, the measure of angle OXZ is 10°.
Given that, XY and ZY are tangents to a circle with center O.
What is the angle formed with tangent and radius?Tangent and radius of a circle meet at 90°. If we draw a radius that meets the circumference at the same point, the angle between the radius and the tangent will always be exactly 90°.
Here, angle formed at the center is
∠ZOX = 180° - ∠XYZ
∠ZOX = 180° - 20°
∠ZOX = 160°
ZO = XO = radius
Now, ΔZOX is an isosceles triangle
So, ∠ZOX +∠OXZ+∠OZX = 180°
⇒ 160° + 2∠OXZ = 180°
⇒ 2∠OXZ = 20°
⇒ ∠OXZ = 10°
Therefore, from the given figure, the measure of angle OXZ is 10°.
To learn more about the tangents to a circle visit:
https://brainly.com/question/23265136.
#SPJ1
Can someone please explain how to do this ?

Answers
Answer:
1) 26
2) 5
3) 20
Step-by-step explanation:
1. 7 x 3 + 5 Do Multiplication before addition
21 + 5
26
2. 8÷4 + 3 Do division before addition
2 + 3
5
3. 2(12-4) + 4 Do what is in the parentheses first
2(8) + 4 Multiply before you add
16 + 4
20
HELP WITH INEQUALITY PROBLEM PLEASE!!!

Answers
Answer:
A. s+7726>=12,600
Step-by-step explanation:
s is the number of steps left to reach her goal of at least 12,600 steps.
7726 is the number of steps already taken.
12,600 is her goal.
s+7726>=12,600
Hope this helps!
Please mark as brainliest if correct!
1) To the nearest tenth of a foot, what is the distance from the wall to
the base of the ladder?
A) 1.9 feet
B) 2.1 feet
C)45 feet
D) 10.7 feet
2) To the nearest tenth of a foot, what is the height at which the ladder
rests against the wall?
A) 2.1 feet
B) 3.7 feet
C) 45 feet
D) 10.7 feet

Answers
Answer:
1) B
2) 4.5 feet
Step-by-step explanation:
Please see the attached picture for the full solution.

product of -2/3 and 5 2/4?
Answers
Answer: \(-\frac{11}{3}\)
Step-by-step explanation:
\(-\frac{2}{3} *5\frac{2}{4} \\\\\\=-\frac{2}{3} *5\frac{1}{2} (5\frac{1}{2} =\frac{5*2}{2} +\frac{1}{2} =\frac{10+1}{2} =\frac{11}{2})\\\\\\=-\frac{2}{3} *\frac{11}{2} =-\frac{11}{3}\)
find the area of each circle round to the nearest tenth use 20 yard
Answers
Answer:
Step-by-step explanation:
Answer:
what circle
Step-by-step explanation:
use the binomial theorem to find the binomial expansion of the given expression. (2x-3y)^5.
show work
Answers
Answer:
(a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^(n-1) b^1 + C(n, 2)a^(n-2) b^2 + ... + C(n, n-1)a^1 b^(n-1) + C(n, n)a^0 b^n
The binomial expansion of (2x - 3y)^5 is:
32x^5 - 240x^4y + 720x^3y^2 - 1080x^2y^3 + 810xy^4 - 243y^5
The binomial expansion of the given expression is 32x⁵+240x⁴y+720x³y²+1080x²y³+810xy⁴+243y⁵.
The given expression is (2x-3y)⁵.
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial.
(2x)⁵+⁵c₁(2x)⁴(3y)¹+⁵C₂(2x)³(3y)²+⁵C₃(2x)²(3y)³+⁵C₄(2x)(3y)⁴+⁵C₅(3y)⁵
= 32x⁵+5(16x⁴)(3y)+10.(8x³)(9y²)+10(4x²)(27y³)+5(2x)(81y⁴)+243y⁵
= 32x⁵+240x⁴y+720x³y²+1080x²y³+810xy⁴+243y⁵
Therefore, the binomial expansion of the given expression is 32x⁵+240x⁴y+720x³y²+1080x²y³+810xy⁴+243y⁵.
To learn more about the binomial expansion visit:
https://brainly.com/question/31363254.
#SPJ2
Suppose a company wants to introduce a new machine that will produce a marginal annual savings in dollars given by S '(x)= 175 - x^2, where x is the number of years of operation of the machine, while producing marginal annual costs in dollars of C'(x) = x^2 +11x. a. To maximize its net savings, for how many years should the company use this new machine? b. What are the net savings during the first year of use of the machine? c. What are the net savings over the period determined in part a?
Answers
a) To maximize its net savings, the company should use the new machine for 7 years. b) The net savings during the first year of use of the machine are $405 (rounded off to the nearest dollar). c) The net savings over the period determined in part a are $1,833.33 (rounded off to the nearest cent).
Step-by-step explanation: a) To determine for how many years should the company use the new machine to maximize its net savings, we need to find the value of x that maximizes the difference between the savings and the costs.To do this, we need to first calculate the net savings, N(x), which is given by:S'(x) - C'(x) = 175 - x² - (x² + 11x) = -2x² - 11x + 175To find the maximum value of N(x), we need to find the critical values, which are the values of x that make N'(x) = 0:N'(x) = -4x - 11 = 0 ⇒ x = -11/4The critical value x = -11/4 is not a valid solution because x represents the number of years of operation of the machine, which cannot be negative. (i.e., not use it at all).However, this answer does not make sense because the company would not introduce a new machine that it does not intend to use. Therefore, we need to examine the concavity of N(x) to see if there is a local maximum in the feasible interval.
To know more about maximizes visit:
https://brainly.com/question/30072001
#SPJ11
True or false? the interval [1,2] contains exactly two numbers - the numbers 1 and 2.
Answers
The answer is "false". The interval [1, 2] contains all the real numbers between 1 and 2 including the endpoints.
How to write and represent an interval?An interval notation is used for representing the continuous set of real values. This is the shortest way of writing inequalities.
Intervals are represented within the brackets such as square brackets or open brackets(parenthesis).
If the interval is within a square bracket, then the end values are included in the set of values.If the interval is within parenthesis, then the end values are not included in the set of values.The square brackets represent the inequalities - 'greater than or equal or 'less than or equalThe parenthesis represents the inequalities - 'greater than' or 'less thanFinding true or false:The given interval is [1, 2]
The given statement is - 'the interval [1, 2] contains exactly two numbers - the numbers 1 and 2'
The given statement is 'false'.
This is beacuse, an interval consists set of all the real values in between the two values given.
So, according to the definition, there are not only the end values but also many real values in between them.
Thus, the answer is "false". The interval [1, 2] consists of all the real values between 1 and 2 including 1 and 2.
Learn more about interval notation here:
https://brainly.com/question/10878781
#SPJ4
Please due tomorrow!!!!!!
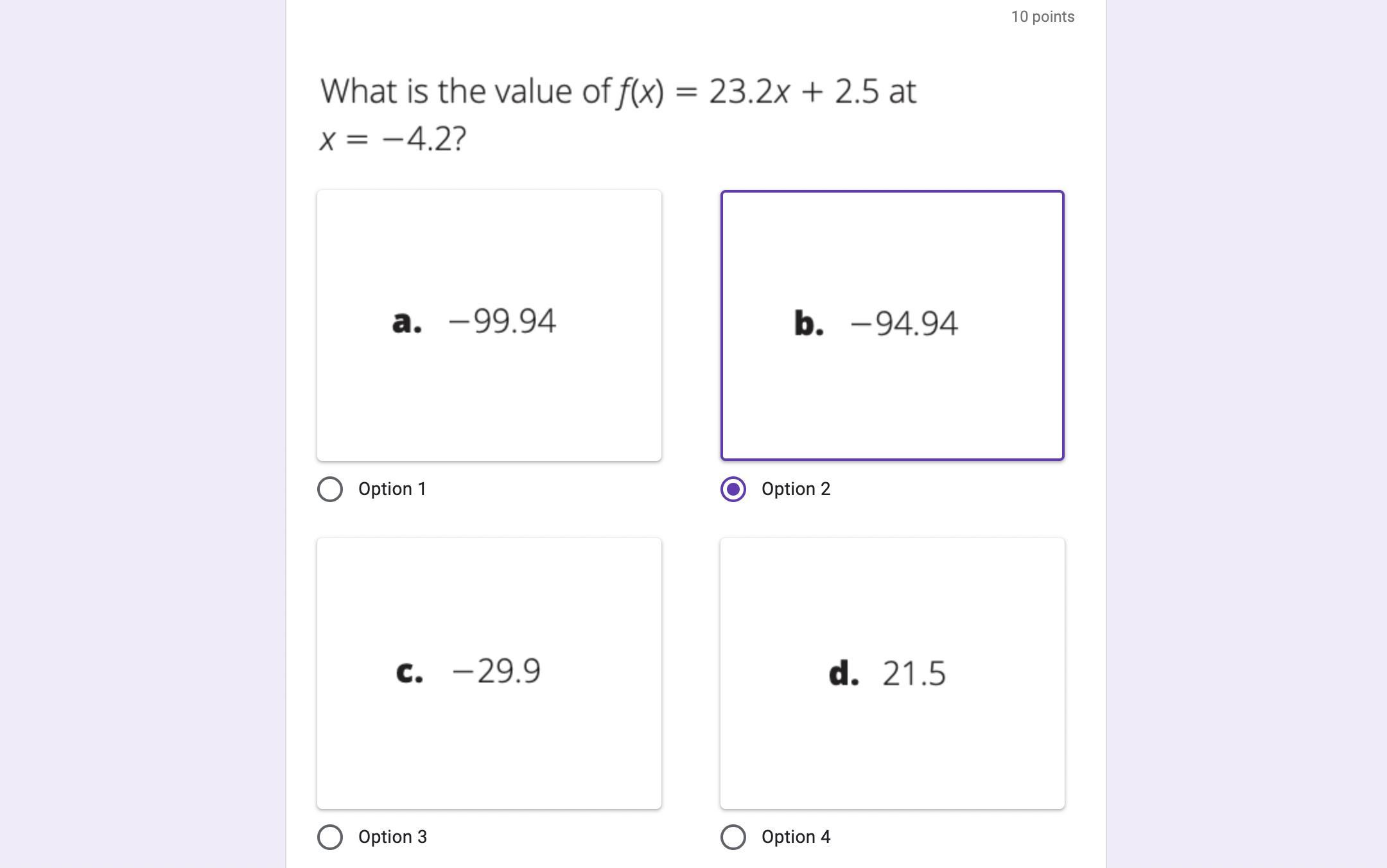
Answers
Answer:
B. -94.94
Step-by-step explanation:
Substitute given value into function and evaluate
Answer:
-94.94
Step-by-step explanation:
The answer is -94.94. First you put -4.2 as x, so 23.2*-4.2 which gives you -97.44. Then you do (-97.44)+22.5. Which gives you the answer -94.94.
What is the value of the expression -7 × 5.4? Record your answer in the grid. Be sure to use correct place value
Answers
Step-by-step explanation:
n -1 077 1/ 7198
12710 27];8w4[' 4108472 1p4201
\421 -]462] -40182 4 '12;il4y01
Can someone plz help Me?

Answers
the answer to your question is C. 6^4
Answer:C? sorry if im wrong
Step-by-step explanation:
Which one of these answers is correct (show work please)
ignore the ones that start with i,ii, iii
100 POINTS!!!

Answers
Answer:
(5) - Option C, \(s=3\sqrt{17}\)
(6) - Option D, \(-\frac{1}{4} y^{-4}=\frac{1}{3} x^3 -\frac{1}{4}\)
Step-by-step explanation:
Given the following questions.
(5) - Find the arc length of y=4x-3 from A(1,1) to B(4,13)
(6) - Solve the first-order differential equation \(y'=x^2y^5\) with the initial condition, \(y(0)=1\).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Question #5:
\(\boxed{\left\begin{array}{ccc}\text{\underline{Formula for Arc Length:}}\\\\s=\int\limits^b_a {\sqrt{1+(f'(x))^2} } \, dx \end{array}\right}\)
(1) - Take the derivative of the function y
\(y=4x-3\\\\\Longrightarrow \boxed{y'=4}\)
(2) - Square y'
\(y'=4\\\\\Longrightarrow y'=4^2\\\\\Longrightarrow \boxed{y'=16}\)
(3) - Plug into the formula for arc length
\(s=\int\limits^b_a {\sqrt{1+(f'(x))^2} } \, dx \\\\\text{Limits:} \ 1\leq x\leq 4\\\\\Longrightarrow\int\limits^4_1 {\sqrt{1+16} } \, dx \\\\\Longrightarrow\boxed{ \int\limits^4_1 {\sqrt{17} } \, dx} \\\)
(4) - Solve the integral
\(\int\limits^4_1 {\sqrt{17} } \, dx \\\\\Longrightarrow \Big [x\sqrt{17} \Big] \right]_{1}^{4}\\\\\Longrightarrow 4\sqrt{17} -\sqrt{17\\}\\\\ \therefore \boxed{s=3\sqrt{17} }\)
Thus, the arc length is found.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Quick note: The question solved for the arc length using a dy integral not a dx integral (which was really unnecessary), so let me clarify that issue.
(1) - Taking the function y, and solving it for x
\(y=4x-3\\\\\Longrightarrow y+3=4x\\\\\Longrightarrow \boxed{x=\frac{1}{4}y+\frac{3}{4}}\)
(2) - Repeating steps (1)-(4) from above
\(x=\frac{1}{4}y+\frac{3}{4}\\\\\Longrightarrow \boxed{x'=\frac{1}{4}} \\\\\Longrightarrow (x')^2=(\frac{1}{4})^2\\\\\Longrightarrow \boxed{(x')^2=\frac{1}{16}}\\\\s=\int\limits^b_a {\sqrt{1+(f'(x))^2} } \, dy\\\text{Limits:} \ 1\leq y\leq 13\\\\ \Longrightarrow\int\limits^{13}_1 {\sqrt{1+\frac{1}{16} } \, dy\\\\ \Longrightarrow\int\limits^{13}_1 {\sqrt{\frac{17}{16} } \, dy\\\\ \Longrightarrow\int\limits^{13}_1 {\frac{\sqrt{17} }{4} } \, dy\\\\\)
\(\Longrightarrow\Big[\frac{\sqrt{17} }{4} y \Big]^{13}_{1}\\\\\Longrightarrow \frac{13\sqrt{17} }{4} -\frac{\sqrt{17} }{4} \\\\\ \Longrightarrow \boxed{\boxed{s=3\sqrt{17} }}\)
Thus, the correct setup according to your question is option C.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Question #6:
The given differential equation is separable.
\(\boxed{\left\begin{array}{ccc}\text{\underline{Seperable Differential Equation:}}\\\frac{dy}{dx} =f(x)g(y)\\\\\rightarrow\int\frac{dy}{g(y)}=\int f(x)dx \end{array}\right }\)
(1) - Solve the separable DE
\(\frac{dy}{dx} =x^2y^5\\\\\Longrightarrow \frac{1}{y^5} dy=x^2dx\\\\\Longrightarrow \int y^{-5}dy= \int x^2 dx\\\\\Longrightarrow \boxed{ -\frac{1}{4} y^{-4}=\frac{1}{3} x^3 +C}\)
(2) - Use the given initial condition to find the arbitrary constant "C"
\(\text{Recall} \rightarrow y(0)=1\\\\-\frac{1}{4} y^{-4}=\frac{1}{3} x^3 +C\\\\\Longrightarrow -\frac{1}{4} (1)^{-4}=\frac{1}{3} (0)^3 +C\\\\\Longrightarrow -\frac{1}{4} (1)=0 +C\\\\\therefore \boxed{C=-\frac{1}{4} }\)
(3) - Form the final solution
\(\boxed{\boxed{-\frac{1}{4} y^{-4}=\frac{1}{3} x^3 -\frac{1}{4} }}\)
Thus, option D is correct.
Answer:
\(\textsf{5.} \quad \textsf{C)} \;\; \displaystyle \int^{13}_1 \sqrt{1+\left(\frac{1}{4}\right)^2}\; \text{d}y\)
\(\textsf{6.} \quad \textsf{D)} \quad -\dfrac{1}{4}y^{-4}=\dfrac{1}{3}x^3-\dfrac{1}{4}\)
Step-by-step explanation:
Question 5To find the arc length of a given function between two points, we can use the Arc Length Formula:
\(\boxed{\begin{minipage}{7.4cm}\underline{Arc Length Formula}\\\\$\displaystyle \int_{a}^{b} \sqrt{1+(f'(x))^2}\; \text{d}x$\\\\\\where: \\ \phantom{ww}$\bullet$ $a$ and $b$ are the limits. \\ \phantom{ww}$\bullet$ $f'(x)$ is the first derivative of $f(x)$.\\\end{minipage}}\)
The given function is:
\(y=4x-3\)
Differentiate the given function:
\(\begin{aligned} f(x)&=4x-3\\ \implies f'(x)&=4\end{aligned}\)
As the function is in terms of x, the interval [a, b] is the x-values of the given points. Therefore:
\(a = 1\)\(b = 4\)Set up the integral using the arc length formula:
\(\displaystyle \textsf{Arc length}=\int^4_1 \sqrt{1+(4)^2}\; \text{d}x\)
You will notice that this integral is not one of the given answer options.
We can also set up the integral with respect to y.
To do this, begin by rearranging the function so that x is a function of y:
\(\begin{aligned}y&=4x-3\\y+3&=4x\\x&=\dfrac{1}{4}y+\dfrac{3}{4}\end{aligned}\)
Differentiate x with respect to y:
\(\begin{aligned} g(y)&=\dfrac{1}{4}y+\dfrac{3}{4}\\ \implies g'(y)&=\dfrac{1}{4}\end{aligned}\)
As the function is in terms of y, the interval [a, b] is the y-values of the given points. Therefore:
\(a = 1\)\(b = 13\)Set up the integral using the arc length formula:
\(\boxed{\displaystyle \textsf{Arc length}=\int^{13}_1 \sqrt{1+\left(\frac{1}{4}\right)^2}\; \text{d}y}\)
Therefore, the correct answer option is option C.
\(\hrulefill\)
Question 6The given differential equation is:
\(\dfrac{\text{d}y}{\text{d}x}=x^2 \cdot y^5\)
Solving a differential equation means using it to find an equation in terms of the two variables, without a derivative term.
Rearrange the equation so that all the terms containing y are on the left-hand side, and all the terms containing x are on the right-hand side:
\(\dfrac{1}{y^5}\; \text{d}y=x^2 \; \text{d}x\)
Integrate both sides:
\(\displaystyle \int \dfrac{1}{y^5}\; \text{d}y=\int x^2 \; \text{d}x\)
Use the following integration rule:
\(\boxed{\begin{minipage}{4 cm}\underline{Integrating $x^n$}\\\\$\displaystyle \int x^n\:\text{d}x=\dfrac{x^{n+1}}{n+1}+\text{C}$\end{minipage}}\)
Therefore:
\(\begin{aligned}\displaystyle \int \dfrac{1}{y^5}\; \text{d}y&=\int x^2 \; \text{d}x\\\\ \int y^{-5}\; \text{d}y&=\int x^2 \; \text{d}x\\\\\dfrac{y^{-5+1}}{-5+1}&=\dfrac{x^{2+1}}{2+1}+\text{C}\\\\\dfrac{y^{-4}}{-4}&=\dfrac{x^3}{3}+\text{C}\\\\-\dfrac{1}{4}y^{-4}&=\dfrac{1}{3}x^3+\text{C}\end{aligned}\)
Given y(0) = 1, substitute y = 1 and x = 0 into the equation and solve for C:
\(\begin{aligned}-\dfrac{1}{4}(1)^{-4}&=\dfrac{1}{3}(0)^3+\text{C}\\\\-\dfrac{1}{4}&=0+\text{C}\\\\\text{C}&=-\dfrac{1}{4}\end{aligned}\)
Therefore, the equation is:
\(\boxed{-\dfrac{1}{4}y^{-4}=\dfrac{1}{3}x^3-\dfrac{1}{4}}\)
Therefore, the correct answer option is option D.
A popular kid's game has 15 tiles and 1 open space. The goal of the game is to rearrange the tiles to put them in order (from least to greatest, starting at the upper left-hand corner and going across each row). Use the figure to write the transformation(s) that describe the path of where the 8 tile is currently, and where it must be by the end of the game. Can this same translation be used to describe the path of all the tiles?

Answers
The translation that describe the path of the 8 tile to reach it's final position is given as follows:
(x,y) -> (x + 3, y - 1).
This same translation cannot be used to describe the path of all tiles, as some will move up, some down, some left and some right, but the movement is not the same for all tiles.
What are the translations?There are four translations that are standard, and their rules are defined as follows:
Translation left a units: (x,y) -> (x - a, y).Translation right a units: (x,y) -> (x + a, y).Translation up a units: (x, y) -> (x, y + a).Translation down a units: (x,y) -> (x, y - a).The tiles will be placed in order, meaning that the tile number eight should be the second row and fourth column.
As the tile with the number eight is at the first row and the first column, the movements are given as follows:
3 units right: x -> x + 3.1 unit down: y -> y - 1.Hence the compound translation is given as follows:
(x,y) -> (x + 3, y - 1).
This, however, cannot be used for all the points, as some of them, for example 5 and 6, are already in their final position, while the movement for tile 1 is 2 units up.
More can be learned about translations at brainly.com/question/29211183
#SPJ1
COILD SOMEONE DO THIS PROBLEM FOR PLEASE!! LOOK AT THE IMAGE ABOVE! Show full work pls it’s due today

Answers
9514 1404 393
Answer:
c. x = 1
Step-by-step explanation:
c. The Pythagorean theorem applies. The square of the hypotenuse is the sum of the squares of the other two sides.
2² = x² +(√3)²
4 = x² +3
1 = x² . . . . . . subtract 3
1 = x . . . . . . . take the square root
In ΔTUV, UV = 14, VT = 19, and TU = 9. Which statement about the angles of ΔTUV must be true?
Answers
In ΔTUV, UV = 14, VT = 19, and TU = 9, The statement about the angles of ΔTUV that must be true is \(m \angle U > m \angle T > \angle V\) Option 5
This is further explained below.
What are angles?Generally, A triangle's angle is a measurement of the length of the side that is perpendicular to it.
This indicates that if one of the sides is longer in length, then the measure of the angle opposite to it will also be longer.
The angles in the triangle TUV are denoted by the symbols T, U, and V.
The side that is UV, TV, and T U correspondingly is the side that is opposite to these angles.
The length of the opposing sides will immediately determine the measure of the angles, which will be directly proportionate to those angles.
since V T>U V>T U, the arrangement of angles will correspond to this as follows: \(m \angle U > m \angle T > \angle V\) Option 5
Read more about angles
https://brainly.com/question/28451077
#SPJ1
CQ
In $\triangle T U V$, UV $=14, V T=19$, and $T U=9$. Which statement about the angles of $\triangle T U V$ must be true?
$\mathrm{m} \angle V>\mathrm{m} \angle T>\mathrm{m} \angle U$
$\mathrm{m} \angle T>\mathrm{m} \angle U>\mathrm{m} \angle V$
$\mathrm{m} \angle U>\mathrm{m} \angle V>\mathrm{m} \angle T$
$m \angle V>m \angle U>m \angle T$
$m \angle U>m \angle T>m \angle V$
$\mathrm{m} \angle T>\mathrm{m} \angle V>\mathrm{m} \angle U$
Use algebra to find the measure of the angles in the pair of complementary angles below. Show your work.

Answers
Answer:
18 and 72
Step-by-step explanation:
4x+x=90
5x=90
divided by 5
x=18
for the first side, since you only have x, you put 18
for the second one, since 4x, 4(18)=72
hope this helps!
what is the ratio of the area of triangle to the area of triangle ? express your answer as a common fraction.
Answers
Thus, the ratio of the area of larger triangle to the area of smaller triangle
is found as 5:1.
Explain about the ratios:An instrument for comparing the sizes of two or more quantities in proportion to one another is called a ratio. A list of the structured equivalent ratios of every given ratio is called a ratio table. By multiplying as well as dividing the 2 terms of such a ratio by an identical number, equivalent ratios can be created.
Given data:
Dimension of larger triangle: base B = 10 cm, Height H = 5 cm.Dimension of smaller triangle : base b = 5 cm, Height H = 2 cm.Area of triangle = 1/2* base * height
Ratios:
area of larger triangle / area of smaller triangle = (1/2*B*H) / (1/2*b*h)
area of larger triangle / area of smaller triangle = B*H / b*h
area of larger triangle / area of smaller triangle = 10*5 / 5*2
area of larger triangle / area of smaller triangle = 50 / 10
area of larger triangle / area of smaller triangle = 5/ 1 = 5:1
Thus, the ratio of the area of larger triangle to the area of smaller triangle
is found as 5:1.
Know more about the ratios:
https://brainly.com/question/12024093
#SPJ1
Complete question:
what is the ratio of the area of larger triangle to the area of smaller triangle ? express your answer as a common fraction.
Dimension of larger triangle: base B = 10 cm, Height H = 5 cm.
Dimension of smaller triangle : base b = 5 cm, Height H = 2 cm.
how much does a typical water bed weigh? useful data: 1 cubic foot of water weighs 64.2 pounds and a typical water bed holds 28 cubic feet of water.
Answers
A typical water bed weighs around 1797.6 pounds. It depends upon the volume of water bed and the unit conversion of the weight and volume units.
What is the typical water bed weigh?A typical water bed holds 28 cubic feet of water.
The volume of the typical water bed and its weight can be calculated with the help of the quantities:
Identify the volume of water held by the water bed, which is 28 cubic feet.
Multiply the volume by the weight of 1 cubic foot of water, which is 64.2 pounds.
Perform the calculation: 28 cubic feet × 64.2 pounds per cubic foot = 1797.6 pounds.
Therefore, a typical water bed weighs approximately 1797.6 pounds when filled with water.
Learn more about Typical water bed here:
https://brainly.com/question/28587577
#SPJ11
A special packet of breakfast cereal contains 20% more than a normal packet. The special packet contains
600 g of cereal. How much cereal does the normal packet contain?
I
Answers
Answer:
480 g of cereal ...........
Use truth tables to determine whether the formula (p∧ ¬q) → (p∧q) is true whenever ¬p is true.
Answers
The formula (p∧ ¬q) → (p∧q) is true whenever ¬p is true. The formula holds true regardless of the truth value of q when p is false.
To determine the truth value of the formula (p∧ ¬q) → (p∧q) when ¬p is true, we need to construct a truth table.
Let's consider the variables p and q and their respective truth values. Since ¬p is true, p must be false.
p q ¬q p∧ ¬q p∧q (p∧ ¬q) → (p∧q)
F T F F F T
F F T F F T
In the truth table above, we evaluate the truth values of the individual components of the formula and then determine the truth value of the entire formula. As we can see, regardless of the value of q, the formula evaluates to true. Thus, the formula (p∧ ¬q) → (p∧q) is true when ¬p is true.
Based on the truth table, we can conclude that the formula (p∧ ¬q) → (p∧q) is true whenever ¬p is true. The formula holds true regardless of the truth value of q when p is false.
To know more about (p∧ ¬q) → (p∧q), visit;
https://brainly.com/question/33645558
#SPJ11
What evidence is needed to prove two triangles are similar by the SSS similarity theorem?
Answers
Consider the same figure as given above. It is observed that DP/PE = DQ/QF and also in the triangle DEF, the line PQ is parallel to the line EF.
So, ∠P = ∠E and ∠Q = ∠F.
Hence, we can write: DP/DE = DQ/DF= PQ/EF.
The above expression is written as
DP/DE = DQ/DF=BC/EF.
It means that PQ = BC.
Hence, the triangle ABC is congruent to the triangle DPQ.
(i.e) ∆ ABC ≅ ∆ DPQ.
Thus, by using the AAA criterion for similarity of the triangle, we can say that
∠A = ∠D, ∠B = ∠E and ∠C = ∠F.
To know more about triangle check the below link:
https://brainly.com/question/1058720
#SPJ4
PLEEEEEEEEEASE HELP!!!

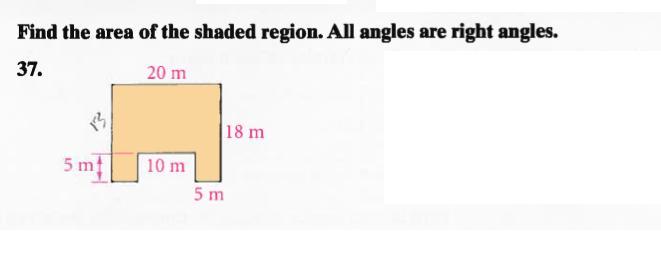

Answers
26.= 6000ft.
1.convert the yards to feet 100 yards= 300 ft
2. to find the area multiply the 20 ft by 300 ft
3. answer is 6000 ft
4 . if the answer needs to be in yards use a converter to convert the feet to yards
IWILL GIVE BRAINLIEST!!!

Answers
Answer:
Step-by-step explanation:


Please show detailed algebraic work.

Answers
Using the given exponential decay model for carbon-14, we found that the painting is approximately 10,521 years old.
What is meant by exponential functions?
A mathematical function called an exponential function is employed frequently in everyday life. It is generally used to find exponential decay or exponential growth. When the input variable x appears as an exponent in the formula f(x) = axe, an exponential function is indicated. When there is exponential growth, the quantity grows initially extremely slowly and subsequently quickly. Throughout time, the rate of change quickens. As time goes on, the rate of increase accelerates. With exponential decay, the quantity initially falls very quickly and then gradually. Throughout time, the rate of change slows. As time goes on, change happens at a slower rate.
The exponential decay model for carbon-14 is given as:
\(A = A_0e^{(-0.000121t)}\)
where,
A = Percentage remaining
A₀ = Initial amount
t = Time in years
Given,
A = 28% of A₀ = 0.28A₀
Substituting in the above exponential decay model,
\(A = A_0e^{(-0.000121t)}\\\\0.28A_0 = A_0e^{(-0.000121t)}\\\\0.28 = e^{(-0.000121t)}\\\\\)
ln 0.28 = -0.000121t
-1.273 = -0.000121t
t = 10,520.66 years = 10,521 years
Therefore using the given exponential decay model for carbon-14, we found that the painting is approximately 10,521 years old.
To learn more about exponential decay, follow the link.
https://brainly.com/question/27822382
#SPJ1