Select the correct answer from each drop-down menu.
A new company is looking to expand its business. The table shows the number of months, x, that have passed since the company was
established, and the number of employees, f(x), at each time period.
x 0 2 4 6 8
f(x) 2 31 54 71 82
Use the data in the table to create the standard form of the function that models this situation.
f(x) =

The domain, range, x-intercept, or y-intercept of g(x) = f(x + 4) + 8. The features of g depend on the corresponding features of f.

Given the function g(x) = f(x + 4) + 8, let's examine its features:

Domain:

The domain of the function g will be the same as the domain of the function f, which depends on the restrictions or constraints of f.  However, it is important to note that shifting the input by 4 units (x + 4) does not inherently change the domain unless there are specific restrictions imposed by f.

Range:

Similar to the domain, the range of the function g will depend on the range of the function f.

x-intercept:

The x-intercept of a function is the point where the graph intersects the x-axis, meaning the y-coordinate is zero (y = 0). To find the x-intercept of g(x), we set g(x) = 0 and solve for x.

0 = f(x + 4) + 8

By subtracting 8 from both sides:

-8 = f(x + 4)

Since the exact value of x that makes f(x + 4) equal to -8. The x-intercept will depend on the behavior of f.

y-intercept:

The y-intercept of a function is the point where the graph intersects the y-axis, meaning the x-coordinate is zero (x = 0). To find the y-intercept of g(x), we substitute x = 0 into the function:

g(0) = f(0 + 4) + 8

g(0) = f(4) + 8

Again, the specific value of f(4) will depend on the behavior of the function f.

for such more question on function

https://brainly.com/question/14723549

#SPJ8

Answer:

x=-pie/12

sinxcosx=-1/4

multiply both sides by 2

sin2x = 2sinxcosx we know

now equation will be

sin2x = -1/2

2x=-pie/6

x=-pie/12

Answer:

-3.64%

Step-by-step explanation:

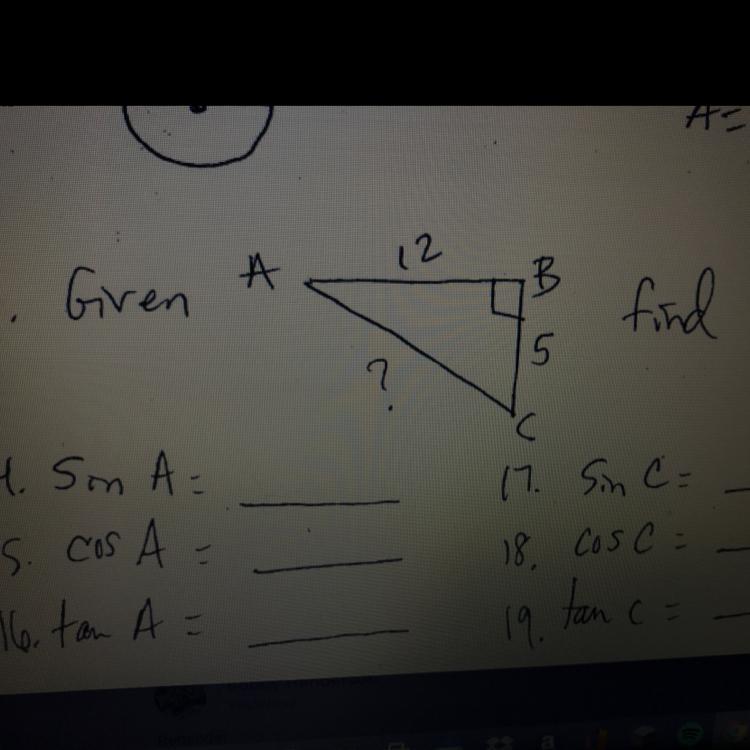
Answer:

SinA=5/1 3 CosA=12/13 tanA=5/12. SinC=12/13 CosC=5/13 and tanC=12/5

Step-by-step explanation:

Basically find the third side by Pythagorean theorem which would get you 13. So 13 is the hypotenuse. Remember these 3 formulas. Sin=Opposite/Hypotenuse Cos=Adjacent/hypotenuse and Tan=opposite/Adjacent. So for Sin a the opposite side to angle A is 5. The hypotenuse is always the same which would be 13. So Sin a is 5/13. For cos the side adjacent would be 12. So it is 12/13. *Note Hypotenuse cannot be considered the adjacent.

Answer:

sin A = 5/13,  cos A = 12/13,  tan A = 5/12,  sin C = 12/13, cos C = 5/13, tan C = 12/5

Step-by-step explanation:

According to Pythagoras, hypotenuse = √{(12)^2+(5)^2}. So, hypotenuse = 13. (See picture if confused).

sin A = 5/13

cos A = 12/13

tan A = 5/12

sin C = 12/13

cos C = 5/13

tan C = 12/5

Answer:

121.1

Step-by-step explanation:

By law of sines, (sin <I)/i = (sin <J)/j. Plugging in the values we know, we get sin 72deg / 206 = sin 34deg / j. When we solve for k, we get that it is about 121.122. Rounded to the nearest tenth, we get that j is 121.1.

Answer:

21. x = 18.1

22. x =28.7

Step-by-step explanation:

SOH = sin(theta) = opp/hyp

CAH = cos(theta) = adj/hyp

TOA = sin(theta) = opp/adj

21. You would be using tangent.

tan(theta) = Opp/Adj

tan(32°) = x/29

x = 29 * tan(32°)

x = 18.1

22. You would be using cosine

cos(theta) = Adj/Hyp

cos(43°) = 21/x

x * cos(43°) = 21

x = 21 / cos(43°)

x = 28.7

Use a Calculator to help you solve for those side lengths or degrees.

If you were to search of SOHCAHTOA online and find an image you would be able to see their example problem done using

I am not sure if I am allowed to use an online example image since I got warned for some reason without explanation to the warning.

Answer:

y = 2x + 10

Step-by-step explanation:

Hi there!

We are given the points (-7, -4) and (-6, -2) and we want to write the equation of the line that passes through these points in slope-intercept form

Slope-intercept form is given as y=mx+b, where m is the slope and b is the y intercept

First, we need to find the slope (m) of the line

The slope can be calculated from 2 points using the formula \(\frac{y_2-y_1}{x_2-x_1}\), where \((x_1, y_1)\) and \((x_2, y_2)\) are points

We have everything we need to find the slope, but let's label the values of the points to avoid any confusion & and mistakes

\(x_1= -7\\y_1=-4\\x_2=-6\\y_2=-2\)

Substitute these values into the formula (note: remember that the formula has subtraction in it!)

m=\(\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{-2--4}{-6--7}\)

Simplify

m=\(\frac{-2+4}{-6+7}\)

Add the numbers

m=\(\frac{2}{1}\)

Divide

m=2

The slope of the line is 2

We can substitute that in:

y = 2x + b

Now we need to find b

As the equation passes through both  (-7,-4) and (-6,-2), we can use either point to help solve for b

Taking (-6, -2) for example:

Substitute -6 as x and -2 as y into the equation.

-2 = 2(-6) + b

Multiply

-2 = -12 + b

Add 12 to both sides

-2 = -12 + b

+12  +12

___________

10 = b

Substitute 10 as b.

y = 2x + 10

Hope this helps!

Topic: Finding the equation of a line

See more on this topic here: https://brainly.com/question/27319082

A function m(t)= m₀e^(-rt) that models the mass remaining after t years is; m(t) = 27e^(-0.00043t)

The amount of sample that will remain after 4000 years is; 4.8357 mg

The number of years that it will take for only 17 mg of the sample to remain is;  1076 years

A) Using the model for radioactive decay;

m(t)= m₀e^(-rt)

where;

m₀ is initial mass

r is rate of growth

t is time

Thus, we are given;

m₀ = 27 mg

r = (In 2)/1600 = -0.00043 which shows a decrease by 0.00043

and so we have;

m(t) = 27e^(-0.00043t)

c) The amount that will remain after 4000 years is;

m(4000) = 27e^(-0.00043 * 4000)

m(4000) = 27 * 0.1791

m(4000) = 4.8357 mg

d) For 17 mg to remain;

17 = 27e^(-0.00043 * t)

17/27 = e^(-0.00043 * t)

In(17/27) = -0.00043 * t

-0.4626/-0.00043 = t

t = 1076 years

Read more about Exponential decay function at; https://brainly.com/question/27822382

#SPJ1

Step-by-step explanation:

it seems you solved the tricky part yourself already.

just to be sure, let's do the first derivative here again.

the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...

f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =

= 3t⁴ + 18t³ + 24t² + 18t + 21

f'(t) = 12t³ + 54t² + 48t + 18

and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).

we simply put the input number (2) at every place of the input variable (t).

so,

f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =

= 426

Answer:

$61.29 per day.

Step-by-step explanation:

Checking account balance on February 1st: $443

Checking account balance on February 7th: $872

Difference in balances: $872 - $443 = $429

Number of days between February 1st and February 7th: 7 days

Rate of change = Difference in balances / Number of days

Rate of change = $429 / 7 days

To find the rate of change per day, divide the difference in balances by the number of days:

Rate of change = $429 / 7 days ≈ $61.29 per day

Therefore, the rate of change in your checking account balance during that period was approximately $61.29 per day.

Explanation:

Segment AW bisects angle CAD.

This leads to the smaller pieces (angles CAW and DAW) to be equal to one another. Both are 20 degrees each. That totals to 20+20 = 40 degrees.

Therefore, angle CAD = 40 degrees.

The supplement of this is angle DAX

(angle CAD) + (angle DAX) = 180

angle DAX = 180 - (angle CAD)

angle DAX = 180 - 40

angle DAX = 140 degrees

Answer:

Step-by-step explanation:

\(\frac{25}{2}\)

Answer:

Given:

Area of the sector (A) = 104π/9 square inches

Central angle (θ) = 65 degrees

The formula for the area of a sector of a circle is:

A = (θ/360) * π * r^2

We can rearrange this formula to solve for the radius (r):

r^2 = (A * 360) / (θ * π)

Plugging in the given values:

r^2 = (104π/9 * 360) / (65 * π)

r^2 = (104 * 40) / 9

r^2 = 4160 / 9

r^2 ≈ 462.22

Taking the square root of both sides:

r ≈ √462.22

r ≈ 21.49

Therefore, the radius of the circle is approximately 21.49 inches.

Answer: 8 inches

Step-by-step explanation:

Problem 1

Reason: We start at 0 and move 4 units left. This is represented by 0+(-4) or 0-4. That simplifies to -4. Then add on 7 to move 7 units to the right to arrive at 3 as the final destination.

=============================================

Problem 2

Reason: We start at 0 and move 8 units to the right. That is represented by +8 or simply 8. Then the +3 will move us 3 more units to the right to get to 11 on the number line. This is one visual way to see why 8+3 = 11.

Answer:

4) Good to Excellent

Answer:

Whats the question?

Step-by-step explanation:

or is it just like a fake question

Answer to the given famous joke is: "The plant in math class forgot to square its roots."

This joke plays on the mathematical concept of "squaring roots" and humorously applies it to a plant in a math class context. In mathematics, "squaring" a number means multiplying it by itself, and the "square root" of a number is the value that, when multiplied by itself, gives the original number.

In this joke, the plant is personified, as if it were a student in a math class, and humorously forgets to square its roots, which is something entirely unrelated to plants but fits within the mathematical context. The humor comes from the unexpected and clever blending of a mathematical concept with a non-mathematical subject, resulting in a lighthearted and punny punchline.

To know more about joke , click here.

https://brainly.com/question/33509840

#SPJ2

------------The given question is incomplete, the complete question is:

"Explain answer to the famous joke, "What happened to the plant in math class?"-----------------

Answer:

2841 no votes

Step-by-step explanation:

Answer:

Step-by-step explanation:

Let's use the following variables:

Let F be the number of sections of Finite Math

Let A be the number of sections of Applied Calculus

Let C be the number of sections of Computer Methods

We can create a system of equations based on the given information:

F + A + C = 7 (the college wishes to offer a total of seven sections)

40F + 60A + 290C = 298000 (the college wishes to bring in $298,000 in revenues)

40F + 40A + 10C = 220 (the college wishes to accommodate 220 students)

We can solve this system of equations using any method we prefer. Here's one possible way:

Multiply the third equation by 10 to get:

400F + 400A + 100C = 2200

Subtract the third equation from the second equation to eliminate C:

20A + 280C = 76000

Multiply the first equation by 40 and subtract it from the previous equation to eliminate A:

240C = 76000 - 1600

Solve for C:

C = 290

Substitute C = 290 into the third equation to solve for F:

40F + 40A + 10(290) = 220

40F + 40A = -2680

F + A = -67

Substitute C = 290 and F + A = -67 into the first equation to solve for A:

A = 10

Substitute A = 10 and C = 290 into the first equation to solve for F:

F = -3

We have a problem here: we obtained a negative number of sections for Finite Math, which is impossible. This means that the original system of equations is inconsistent, and there is no solution that satisfies all the requirements.

Therefore, the college cannot offer the desired number of sections while accommodating the desired number of students and revenue. Some adjustments need to be made, such as changing the number of students per section or the tuition fees.

Answer:

The one of -[n+2n+3n+4n]/nlne(10) has fewer operations because the value of n is static.

The one of n! ( factorial ) is factorised up to n∞ hence has infinity operations.

let's put h(x) in vertex form, and then let's see if we can get f(x) from there.

\(~~~~~~\textit{vertical parabola vertex form} \\\\ y=a(x- h)^2+ k\qquad \begin{cases} \stackrel{vertex}{(h,k)}\\\\ \stackrel{"a"~is~negative}{op ens~\cap}\qquad \stackrel{"a"~is~positive}{op ens~\cup} \end{cases} \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \stackrel{vertex}{\stackrel{h}{0}~~,~~\stackrel{k}{-3}}\qquad h(x)=a(x-0)^2-3 \\\\[-0.35em] ~\dotfill\)

\(h(x+2)=a[(x+2)-0]^2-3\implies h(x+2)=\underline{a(x+2)^2-3} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{llll} \underline{h(x+2)}-5\implies [a(x+2)^2-3]~~ - ~~5\implies &\boxed{a(x+2)^2-8=f(x)} \\\\ &a[x-\stackrel{h}{(-2)}]^2\stackrel{k}{-8}=f(x)\\\\ &\stackrel{vertex}{-2~~,~~-8} \end{array}\)

The solution is,  2.5 miles per hour was her walking rate in miles per hour.

We know that,

Speed is measured as distance moved over time.

The formula for speed is speed = distance ÷ time.

To work out what the units are for speed, you need to know the units for distance and time.

In this example, distance is in metres (m) and time is in seconds (s), so the units will be in metres per second (m/s).

Speed = Distance/ Time.

Here, given that,

Bao walked 15 miles in 6 hours.

so, we get,

in 6 hours = 15 miles

so, in 1 hour = 15 / 6 miles

                    =2.5 miles

Hence, The solution is,  2.5 miles per hour was her walking rate in miles per hour.

To learn more on speed click:

brainly.com/question/28224010

#SPJ1

Answer:

24

Step-by-step explanation:

let Sammy's age be x and Lisa y

since Lisa is 4years older than Sammy

y=x+4

28-4=y

y=24

The measure of angle POQ is given as follows:

30º.

The area of a circle of radius r is given by π multiplied by the radius squared, as follows:

A = πr²

The radius of the circle in this problem is given as follows:

r = OP = 2.

(distance of the center O to point P on the circumference).

Hence the area of the circle is given as follows:

A = 4π.

The area of the sector is given as follows:

π/3.

The ratio of the area of the sector and the area of the circumference is given as follows:

(π/3)/(4π) = 1/12.

The entire area has a measure of 360º, hence the angle measure is obtained as follows:

1/12 x 360 = 30º.

The problem is given by the image presented at the end of the answer.

More can be learned about angle measures at https://brainly.com/question/25716982

#SPJ1

The most effective action that Fatimah can take to reduce the reservoir's amount of water loss is to install an evaporation control system.

What is amount?

Amount is a term used to refer to the quantity or magnitude of something, typically in financial or numerical terms. It can refer to physical items such as money, goods, or services, as well as abstract concepts such as time, distance, or energy. The amount of something is usually determined by measuring, counting, or weighing it.

Evaporation is a major source of water loss in arid regions, as the dry air quickly absorbs the moisture from the reservoir's surface. By installing an evaporation control system, Fatimah can reduce the amount of water lost to evaporation by using a variety of strategies. These strategies can include the use of an impermeable membrane to cover the reservoir's surface, the installation of windbreaks to reduce the speed of the wind over the water, and the use of chemicals to reduce the rate of evaporation. All of these strategies can be used to drastically reduce the amount of water lost to evaporation.

The installation of an evaporation control system can also be relatively inexpensive compared to other solutions. For instance, compared to installing a new water pump system or rerouting water to the reservoir, installing an evaporation control system can be done quickly and at a lower cost. This makes it a more suitable solution for Fatimah's limited budget.

To know more about amount

https://brainly.com/question/24795637

#SPJ1

Answer:

The probability of the complement (no rain) is 0.75 or 75%.

Step-by-step explanation:

The complement of an event A is the probability of A not occurring, which is equal to 1 - P(A).

Given that the probability of rain today is 25%, the probability of no rain (the complement of rain) is:

P(no rain) = 1 - P(rain)

P(no rain) = 1 - 0.25

P(no rain) = 0.75

Therefore, the probability of the complement (no rain) is 0.75 or 75%.

Answer:

19

Step-by-step explanation:

Notice that these two triangles are comprised of the same two lines. Because of this we can assume that \(39 = (2x+1)\)

We can proceed from here.

The parentheses are unnecessary on the right side of the equation because there is nothing else on that side. Lets remove them

\(39=2x+1\)

Now remember that we must do OPPOSITES. do the opposite on both sides. For example lets get rid of the 1. The opposite of 1 is negative 1. So subtract 1 from both sides. We get

\(38=2x\)

now we are making progress.....

the opposite of 2 times x is 2 divided by x. Lets divide 2 from both sides.

\(19=x\)

SUCCESS!