Sean prepared 44 kilograms of dough after working 11 hours. How many hours did Sean work if he prepared 48 kilograms of dough? Assume the relationship is directly proportional.
Answers
This is an example of direct variation.
So, 44 48
11 x
For this, you have to use the formula, 44x = 48 × 11
= (48 × 11) ÷ 44 = 12
Hence, your answer is 12 hours
Related Questions
Dr. Bennington took an alloy containing 10% silver and mixed it with an alloy containing 40% silver to get a 60-ounce alloy containing 30% silver. How many ounces of the 10% alloy did he use?
Answers
Answer:
He used 20 ounces of the 10% alloy.
Step-by-step explanation:
Let x represent the number of ounces of alloy containing 10%
silver that was used.
Let y represent the number of ounces of alloy containing 40%
silver that was used.
The weight of the alloy made is 60 ounces. It means that
x + y = 60
The amount of silver contained in the first alloy is 10/100 × x = 0.1x
The amount of silver contained in the second alloy is 40/100 × x = 0.4x
The amount of silver contained in the mixture is 30/100 × 60 = 18
Therefore,
0.1x + 0.4y = 18- - - - - - - - - - - - -1
Substituting x = 60 - y into equation 1, it becomes
0.1(60 - y) + 0.4y = 18
6 - 0.1y + 0.4y = 18
- 0.1y + 0.4y = 18 - 6
0.3y = 12
y = 12/0.3
y = 40
x = 60 - 40
x = 20
what is the set from least to greatest

Answers
Answer:
the second answer choice
p³p²-p³r² = ...
HELPPPP
Answers
Answer:
p^5 - p^3 r^2
Step-by-step explanation:
Pls somone answer my family is toxic I can’t Finnish pls someone answer plssss :(
Mr. Judge wants to solve the inequality -7x + 4x – 17 ≥ -8. He says the answer is x ≥ -3. Is his answer correct?
Answers
Answer:
so i got x=-3 i didnt get any signs in between
Step-by-step explanation:
Help me pls asap! :)

Answers
Answer:
infinite solutions
4x+ 12 - 4 = 4x + 8
4x + 8 = 4x + 8
Fully simplified slope intercept form

Answers
Step-by-step explanation:
look at the picture
*for the equation you can choose any of the two points

For the pair of points, find the slope of the line that passes through both points.
If you get stuck, try plotting the points on graph paper and drawing the line through them with a ruler.
(2,5) and (-1,2)
Answers
Answer:
Step-by-step explanation:
You would have to go up 2 and then go to your Left 5 .
You would have to go over to your right -1 and then go up 2
Brainliest, 5 stars, and thanks if right

Answers
Answer:
from last question,
x = 25
25 + 15 = 40
I need to know how to solve this

Answers
To find angle y you subtract the two angles form 180 degrees because it is a straight line. Then you subtract angle y and 72 from 180 because a triangle adds up to 180 degrees and you get angle x.
Hope this helps, ask if you have any more questions!
- Evaluate Sc (y + x – 4ix3)dz where c is represented by: C:The straight line from Z = 0 to Z = 1+ i C2: Along the imiginary axis from Z = 0 to Z = i. = =
Answers
The value of the integral C1 and C2 are below:
∫[C1] (y + x – 4ix³) dz = -1/2 + 4/3 i
∫[C2] (y + x – 4ix³) dz = 0
To evaluate the integral, we need to parameterize the given contour C and express it as a function of a single variable. Then we substitute the parameterization into the integrand and evaluate the integral with respect to the parameter.
Let's evaluate the integral along contour C1: the straight line from Z = 0 to Z = 1 + i.
Parameterizing C1:
Let's denote the parameter t, where 0 ≤ t ≤ 1.
We can express the contour C1 as a function of t using the equation of a line:
Z(t) = (1 - t) ×0 + t× (1 + i)
= t + ti, where 0 ≤ t ≤ 1
Now, we'll calculate the differential dz/dt:
dz/dt = 1 + i
Substituting these into the integral:
∫[C1] (y + x – 4ix³) dz = ∫[0 to 1] (Im(Z) + Re(Z) - 4i(Re(Z))³)(dz/dt) dt
= ∫[0 to 1] (t + 0 - 4i(0)³)(1 + i) dt
= ∫[0 to 1] (t + 0)(1 + i) dt
= ∫[0 to 1] (t + ti)(1 + i) dt
= ∫[0 to 1] (t + ti - t + ti²) dt
= ∫[0 to 1] (2ti - t + ti²) dt
= ∫[0 to 1] (-t + 2ti + ti²) dt
Now, let's integrate each term:
∫[0 to 1] -t dt = [-t²/2] [0 to 1] = -1/2
∫[0 to 1] 2ti dt = \(t^{2i}\)[0 to 1] = i
∫[0 to 1] ti² dt = (1/3)\(t^{3i}\) [0 to 1] = (1/3)i
Adding the results together:
∫[C1] (y + x – 4ix³) dz = -1/2 + i + (1/3)i = -1/2 + 4/3 i
Therefore, the value of the integral along contour C1 is -1/2 + 4/3 i.
Let's now evaluate the integral along contour C2: along the imaginary axis from Z = 0 to Z = i.
Parameterizing C2:
Let's denote the parameter t, where 0 ≤ t ≤ 1.
We can express the contour C2 as a function of t using the equation of a line:
Z(t) = (1 - t)× 0 + t × i
= ti, where 0 ≤ t ≤ 1
Now, we'll calculate the differential dz/dt:
dz/dt = i
Substituting these into the integral:
∫[C2] (y + x – 4ix³) dz = ∫[0 to 1] (Im(Z) + Re(Z) - 4i(Re(Z))³)(dz/dt) dt
= ∫[0 to 1] (0 + 0 - 4i(0)³)(i) dt
= ∫[0 to 1] (0)(i) dt
= ∫[0 to 1] 0 dt
= 0
Therefore, the value of the integral along contour C2 is 0.
In summary:
∫[C1] (y + x – 4ix³) dz = -1/2 + 4/3 i
∫[C2] (y + x – 4ix³) dz = 0
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
please help With this question

Answers
Answer:
-1
Step-by-step explanation:
"Gradient" is yet another term for "slope" or "rate of change." It is the ratio of "rise" to "run."
Here, the graph goes through grid intersections such that 1 to the right is 1 down. The "rise" is -1 for a "run" of 1, and the slop (gradient) is ...
m = rise/run = -1/1 = -1
The gradient of the graphed line is -1.
Please answer question

Answers
Answer:
V = 28 mm³Step-by-step explanation:
Base is right triangle, so:
B = ¹/₂•4•6 = 12 mm²
H = 7 mm
V = ¹/₃•B•H
V = ¹/₃•12•7 = 4•7 = 28 mm³
Answer:
V=28 mm³
Step-by-step explanation:
V= volume of the pyramide
G = square of the triangle
h = high of the pyramide
V = 1/3 * G* h
G=1/2 *a*b
G = 1/2 * 6 * 4
G = 12
V= 1/3 *12*7
V=28 mm³
What is the value of the expression 3 ⋅ 10 + 3 + 10 ⋅ 3 2 3⋅10+3+10⋅3 2
Answers
Answer:
Hopes this helps not sure rlly
Step-by-step explanation:
3,277.32
LIT A hemispherical tank on an axis system is shown above. It has radius R = 9 m and it is filled with water A spout is L = 3 m above top of the tank. Find the work required to empty all the water out of the spout. Recall that the gravitational constant is g = 9.8 m The work to empty a full tank is (9.534)(10^7) (p=100 5). R ⠀ X J. (1 point) a b Total Work 21.3(10^6) X A tank in the shape of a right circular cone is shown above on an axis system. Calculate the work (in joules) required to pump all of the liquid out of the full tank. Assume a = 6 m, b = 12 m, liquid exits through the spout, c = 3 m, and density of the liquid is 1200 kg/m³. Recall that the gravitational constant is g = 9.8. EEE
Answers
That Radius R = 9 mL = 3 mg = 9.8 m/sec²Density, p = 1005 kg/m³Work required to empty a full tank = 9.534 × 10⁷ J
A hemispherical tank is given with radius R = 9 m and it is filled with water. A spout is L = 3 m above the top of the tank. We have to find the work required to empty all the water out of the spout.Work done against gravity to empty the water in the tank = mgh.
Here, m = mass of the water in the tankg = gravitational constanth height from the top of the tank to the spoutWe need to find the mass of the water in the tank, then we can easily find the work done against gravity using above formula.To find the mass of water in the tank, we can use the formula of the volume of the hemispherical tank.V = 2/3 πr³
V = 2/3 × π × 9³
V = 2/3 × π × 729
V = 486 π cubic meters1
m³ = 1000 liters1 liter of
water = 1 kg of massWeight of water in the
tank = pVgWeight of water in the
tank = 1005 × 486 π × 9.8Weight of water in the
tank = 4.74 × 10⁶ π NewtonsThe height from the top of the tank to the spout is given as 3 m.The work done against gravity to empty the tank isW = mgh
W = (4.74 × 10⁶ π) × 3 × 9.8
W = 139.97 × 10⁶ π JThe work done against gravity to empty all the water from the tank through the spout is 139.97 × 10⁶ π J.The required work is 139.97 × 10⁶ π J.
To know more about Density visit:
https://brainly.com/question/30636123
#SPJ11
unit 8 right triangle and trigonometry homework 5 trigonometry: finding sides and angles solve for x round to the nearest tenth.
plllls I will make brainlesst

Answers
Answer:
5. x = 25.6
6. x = 11.0
7. x = 41.8°
8. x = 64.2°
9. x = 12.8°
10. x = 51.3°
Step-by-step explanation:
Let's find the x value for each triangle.
For point 5
We have:
x: is the opposite cathetus to 52°
20: is the adjacent cathetus to 52°
52°: is the angle
We can find "x" with the following trigonometric function:
\( tan(52) = \frac{x}{20} \)
\( x = tan(52)*20 = 25.6 \)
For point 6
We have:
x: is the hypotenuse
5: is the opposite cathetus to the given angle
27°: is the angle
To find "x" we need to use the trigonometric function:
\( sin(27) = \frac{5}{x} \)
\(x = \frac{5}{sin(27)} = 11.0\)
For point 7
We know:
x°: is the angle
6: is the hypotenuse
4: is the opposite cathetus to x°
Hence, x is:
\( sin(x) = \frac{4}{6} \)
\( x = sin^{-1}(\frac{4}{6}) = 41.8 \)
For point 8
We have:
x°: is the angle
14: is the adjacent cathetus to x°
29: is the opposite cathetus to x°
To calculate "x" we need to use the trigonometric function tan(x):
\( tan(x) = \frac{29}{14} \)
\( x = tan^{-1}(\frac{29}{14}) = 64.2 \)
For point 9
We have:
x°: is the angle
54: is the hypotenuse
12: is the opposite cathetus to x°
We can use sin(x) to solve for x:
\( sin(x) = \frac{12}{54} \)
\( x = sin^{-1}(\frac{12}{54}) = 12.8 \)
For point 10
We have:
x°: is the angle
40: is the hypotenuse
25: is the adjacent cathetus to x°
We need to use cos(x) to solve for x:
\( cos(x) = \frac{25}{40} \)
\( x = cos^{-1}(\frac{25}{40}) = 51.3 \)
I hope it helps you!
To solve the given questions, either of the trigonometric functions; sine, cosine and tangent of an angle has to be applied appropriately to either of the questions. The answers to the questions are:
5. x = 25.60
6. x = 11.00
7. x = \(41.8^{o}\)
8. x = \(64.2^{o}\)
9. x = \(12.8^{o}\)
10. x = \(51.3^{o}\)
The questions given are right angled triangles which requires the application of trigonometric functions appropriately. A right angle triangle is one that has one of its angles to be \(90^{o}\).
So, each of the questions can be solved as follows:
5. Tan θ = \(\frac{opposite}{adjacent}\)
Tan 52 = \(\frac{x}{20}\)
⇒ x = Tan 52 * 20
= 25.5988
x = 25.60
6. Sin θ = \(\frac{opposite}{hypotenuse}\)
Sin 27 = \(\frac{5}{x}\)
⇒ x = \(\frac{5}{Sin 27}\)
= 11.0134
x = 11.00
7. Sin θ = \(\frac{opposite}{hypotenuse}\)
Sin x = \(\frac{4}{6}\)
= 0.66667
x = \(Sin^{-1}\) 0.66667
= \(41.8^{o}\)
x = \(41.8^{o}\)
8. Tan θ = \(\frac{opposite}{adjacent}\)
Tan x = \(\frac{29}{14}\)
= 2.0714
x = \(Tan^{-1}\) 2.0714
= \(64.2^{o}\)
x = \(64.2^{o}\)
9. Sin θ = \(\frac{opposite}{hypotenuse}\)
Sin x = \(\frac{12}{54}\)
= 0.22222
x = \(Sin^{-1}\) 0.22222
= \(12.8^{o}\)
x = \(12.8^{o}\)
10. Cos θ = \(\frac{adjacent}{hypotenuse}\)
Cos x = \(\frac{25}{40}\)
= 0.625
x = \(Cos^{-1}\) 0.625
= \(51.3^{o}\)
x = \(51.3^{o}\)
Visit: https://brainly.com/question/20926900
Lana has 4 bags of apples. Each bag has 9 apples. She puts an equal number of apples on each of 6 plates.
Let n be the number of apples on each plate.
What equation can be used to find n?
Answers
4x9 to get the total number of apples
Then divide by 6 to see how many apples for each plate (since there’s 6)
At a certain zoo, the average mass of one cow is measured to be 410 kilograms. Usescientific notation to express the mass of 150 cows.
Answers
Step 1:
Given data
The average mass of a cow = 410 kg
Step 2:
To find the mass of 150 cows, you will multiply 150 cows by 410 kg.
Therefore
\(\begin{gathered} \text{Total mass of 150 cows = 150 }\times\text{ 410 } \\ \text{ = 61500 kg} \end{gathered}\)Final answer
Write the total weight in scientific notation
\(=\text{ 6.15 }\times10^4\text{ kg}\)The two tables show the number of copies of albums x, y, and z sold in outlets a, b, c, and d of a company. which outlet sold the greatest number of copies of album x in july and august?
Answers
Outlet A sold the greatest number of copies of album x in July and August
How to determine the outlet?The tables of values are given as:
July
Album X Album Y Album Z
Outlet A 14 8 6
Outlet B 7 13 4
Outlet C 2 11 1
August
Album X Album Y Album Z
Outlet A 12 14 10
Outlet B 5 12 8
Outlet C 16 12 7
In July, the total sales of album x are:
Outlet A = 14
Outlet B = 7
Outlet C = 2
In August, the total sales of album x are:
Outlet A = 12
Outlet B = 5
Outlet C = 16
Add both sales
A = 14 + 12 = 26
B = 7 + 5 = 12
C = 2 + 16 = 18
26 (in outlet A) is greater than 12 and 18
Hence, outlet A sold the greatest number of copies of album x in July and August
Read more about two-way tables at:
https://brainly.com/question/15940356
#SPJ1
Answer:
Outlet D
Step-by-step explanation:
they sold 28 of album x
outlet a only sold 26
A person places $757 in an investment account earning an annual rate of 8.2%, compounded continuously. Using the formula V = Pe^{rt}V=Pe rt , where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 20 years.
Answers
Answer: 3902.4633
Step-by-step explanation: 3902.46 from deltamath
Three-sevenths of a number is 21. Find the number.
the number is 27
the number is 9
the number is 49
Answers
Answer:
the number is 49
Step-by-step explanation:
please mark me brainly please!!!
Please help, it’s not college math!!

Answers
Answer: The first answer choice
AKA: y = -1.74x + 46.6
Step-by-step explanation:
I JUST NEED A SENTENCE OR TWO OF EXPLAINATION.

Answers
Answer: No, your friend is not correct. If the problem was addition, then yes it would equal the same answer, but with subtraction, the answers will be different.
Step-by-step explanation:
why are 4:7, 8:15, 16:28, 20:35 equivalent
Answers
Answer:
I am assuming the 8:15 was a typo and was actually supposed to be a 8:14. Anyways, they are equivalent because they all make 4:7 when simplified.
Step-by-step explanation:
4:7 = itself at this point, as they don't have numbers that can simplify each other on both sides, unless you are looking for a decimal answer.
8:14 = 4:7 <- You can divide the 8 and 14 by two. 8 divided by 2 is four, and 14 divided by 2 is 7.
16:28 = 4:7 <- You can divide the 16 and the 28 by four. 16 divided by 4 is 4, and 28 divided by 4 is 7.
20:35 = 4:7 <- You can divide both sides by 5. 20 divided by 5 is 4, and 35 divided by 5 is 7.
Prove 3n^2 + 6n big theta of (n^2 log n)
Answers
Since 3n² + 6n is both O(n² log n) and Ω(n² log n), we can conclude that it is indeed Θ(n² log n).
To prove that 3n² + 6n is in Θ(n² log n), we need to show both the upper and lower bounds.
First, we will prove the upper bound by showing that 3n² + 6n is O(n² log n). This means we need to find constants c and n₀ such that 3n²+ 6n ≤ c(n² log n) for all n ≥ n₀.
Let's simplify the expression 3n² + 6n:
3n² + 6n ≤ 3n² + 6n² (for n ≥ 1, since n is always positive)
= 9n²
Now, we can set c = 9 and n₀ = 1. For all n ≥ 1:
3n² + 6n ≤ 9n² (which is the same as c(n²))
≤ 9n² log n
Therefore, we have shown that 3n² + 6n is O(n² log n), satisfying the upper bound.
Next, we will prove the lower bound by showing that 3n² + 6n is Ω(n² log n). This means we need to find constants c and n₀ such that 3n²+ 6n ≥ c(n² log n) for all n ≥ n₀.
Let's simplify the expression 3n² + 6n:
3n² + 6n ≥ 3n² (for n ≥ 1, since n is always positive)
= 3n² log n
Now, we can set c = 3 and n₀ = 1. For all n ≥ 1:
3n² + 6n ≥ 3n² log n (which is the same as c(n² log n))
Therefore, we have shown that 3n² + 6n is Ω(n² log n), satisfying the lower bound.
Learn more about upper bound here:
https://brainly.com/question/32676654
#SPJ11
a 90% confidence interval is constructed for the population mean. if a 95% confidence interval had been constructed instead (everything else remaining the same), how will that affect the width of the interval and the probability of making an error? group of answer choices interval width will increase and error will decrease interval width will increase and error will increase interval width will decrease and error will increase interval width will decrease and error will decrease
Answers
The width of the interval would be = Wider
The probability of making an error will be = Smaller
According to the question,
The actual interval to be constructed = 90%
The interval constructed otherwise = 95%
The formula for the width of the confidence interval will be,
W = 2 x CV x \(\frac{\alpha }{\sqrt{n} }\)
Considering,
n = sample size
\(\alpha\) = standard deviation
CV = critical value
Critical value is dependent on the confidence levelCritical value ∝ Confidence levelCritical value ∝ width of confidence level'The bigger the confidence level wider is the intervalConsidering the below table,
Confidence level z,
90% 1.64
95% 1.96
99% 2.58
So the confidence level of 95% will be more than 90%.
Therefore,
The width of the interval would be = Wider
The probability of making an error will be = Smaller
To learn more about z-table,
https://brainly.com/question/18761122
#SPJ4
help me please .
Ester purchased a used car, a Ford Focus, for $8400. The car is expected to decrease in value by 20% per year over the next couple of years.
At this rate, what can Ester expect the approximate value of the car to be after 6 years?
Question 6 options:
$1,409
$2,202
$4,200
$1,762
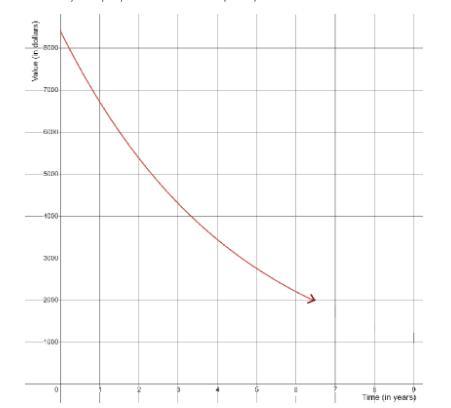
Answers
Answer:
$2,202
Step-by-step explanation:
If the car decreases in value 20% per year, that means that the car is only worth 80% of its value for the next year.
80% can be written as .80.
Multiply the value of the car by .80 6 times.
8400 multiplied by .80 = 6720
6720 multiplied by .80 = 5376
repeat this sequence 4 more times to come to an answer of 2,202
Mary wants to buy a mobile phone; the least expensive one she's spotted so far is $15. Mary has $4.25 saved for a mobile phone. If Mary works at a rate of $2.15 per hour, how many hours (H) will she have to work in order to afford a mobile phone?
Answers
Answer:
Mary would have to work 5 hours to afford a mobile phone.
Step-by-step explanation:
$15-$4.25= $10.75 that Mary would need to save.
2.15 x 5= 10.75
why is important to maintain an assessment’s validity, reliability, and equity in testing?
Answers
Answer: Reliability refers to the degree to which scores from a particular test are consistent from one use of the test to the next. ... Ultimately then, validity is of paramount importance because it refers to the degree to which a resulting score can be used to make meaningful and useful inferences about the test taker
Please helppppp!! Find the midpoint of the segment with the following end points (-2,7) and (2,3)
Answers
Answer:
\( \huge{ \boxed{ \bold{ \tt( \: 0 \: ,5 \: )}}}\)
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
☞ First, Let's explore about Midpoint :
Midpoint of the segment simply means middle point of a line segment. Formula of Midpoint :
\( \boxed{ \sf{(x _{ \: m \: } ,\: y_{m}) = ( \frac{x_{1} + x_{2}}{2} ,\: \frac{y_{1} + y_{2}}{2} )}}\)
where ,
\(( \sf{x_{ \: m \: } ,\: y _{ \: m \: })}\) = co-ordinates of the midpoint\(( \sf{ x_{ \: 1 \: }, \: y_{ \: 1 \: }})\) = co-ordinates of the first point\( \sf{(x _{ \: 2 \: } ,\: y_{ \: 2 \: })}\) = co-ordinates of the second pointThe Midpoint Formula is used to find the exact center point between two defined points in a line segment. The Midpoint formula is quite simple , so you should easily be able to remember it. It won't matter which point you pick to be the 'first" point you plug in. Just make sure that you're adding both an x to an x and a y to a y. Hence, keep in mind , in order to find the midpoint of a line segment, the first step is to add both ' x - co-ordinates' and divide it by 2 and then the second step is to add both ' y - co-ordinates ' and divide it by 2.
Now, Let's solve it!
☯ Question :
Find the midpoint of the segment with the following end points ( - 2 , 7 ) and ( 2 , 3 ).☯ Step - by - step explanation :
Let P ( x , y ) divide the line joining the points A ( - 2 , 7 ) and B ( 2 , 3 ). Now, let :
A ( - 2 , 7 ) → ( x₁ , y₁ )B ( 2 , 3 ) → ( x₂ , y₂ )Apply midpoint formula , then plug the values and lastly simplify it :
\( \sf{ midpoint \: = \: ( \frac{x _{ \: 1 \: } + x _{ \: 2 \: }}{2} , \: \frac{y_{ \: 1 \: } + y _{ \: 2\: }}{2} })\)
➺ \( \sf{midpoint = ( \frac{ - 2 + 2}{2}, \: \frac{7 + 3}{2} )}\)
➺ \( \sf{midpoint = ( \frac{0}{2} , \: \frac{10}{2} )}\)
➺ \( \boxed{ \sf{ midpoint = ( \: 0 \: , 5})}\)
Hence , The midpoint of the segment with the end points A ( - 2 , 7 ) and B ( 2 , 3 ) is ( 0 , 5 ) .
Hope I helped!
Have a wonderful time ッ
~TheAnimeGirl ♡
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁

which sum or difference is modeled by the algebraic tiles?

Answers
Answer:
C
Step-by-step explanation: