Sarah's books has tote bags on sale for $14.65 after a 20% markdown. What is the markdown in dollars?

Answer:

-18

Step-by-step explanation:

-3 × 2 = -6

-6 × 3 = -18

Answer:

The oldest person is 25 years old

Step-by-step explanation:

Represent David's age by d.

Then Dan's age is d + 5, and Bridget's is d - 8.

The sum of these three ages is 57:

d + (d + 5) + (d - 8) = 57

This simplifies to

3d - 3 = 57, or 3d = 60.  Then d must be 20.

David is 20, Dan is 25 (5 years older than David), and Bridget is 12 (8 years younger than David).

Check:  Do these three ages add up to 57?

20 + 25 + 12 = 57   YES\

The oldest person is 25 years old.  That's Dan's age.

Let x represent the number of cars

Let y represent the number of vans

We were told that the maximum capacity of the car is 4 passengers. This means that the number of passengers that x cars would carry is 4 * x = 4x

Also, the maximum capacity of the van is 9 passengers. This means that the number of passengers that y vans would carry is 9 * y = 9y

The total number of vehicles used is 11. It means that

x + y = 11

Also, the 11 vehicles can combine to carry 79 passengers. This means that

4x + 9y = 79

The equations are

x + y = 11

4x + 9y = 79

Answer:

A round pencil is sharpened at both ends the hight of the pencil is 16cm the length of the pencil is 1cm the radius of the two sharpened ends is 16cm 1.2cm

Calculate the volume using the value 22/7. 

Step-by-step explanation:

If we were getting 60% discount early and then again we are receiving 20% discount for using credit card then it means that we are getting 80% discount.

Discount means the amount which is deducted by sellers from the amount to be payable by buyers.

Let the total price to be paid by us to store is $100.

Discount received because on purchase on sale day=100*60%

=60

Discount received due to use of credit card=100*20%

=20

Total discount received from store=60+20

=80

Percentage=80/100*100

=80%

Hence the total discount received by us from store is 80%.

Learn more about percentage at https://brainly.com/question/843074

#SPJ2

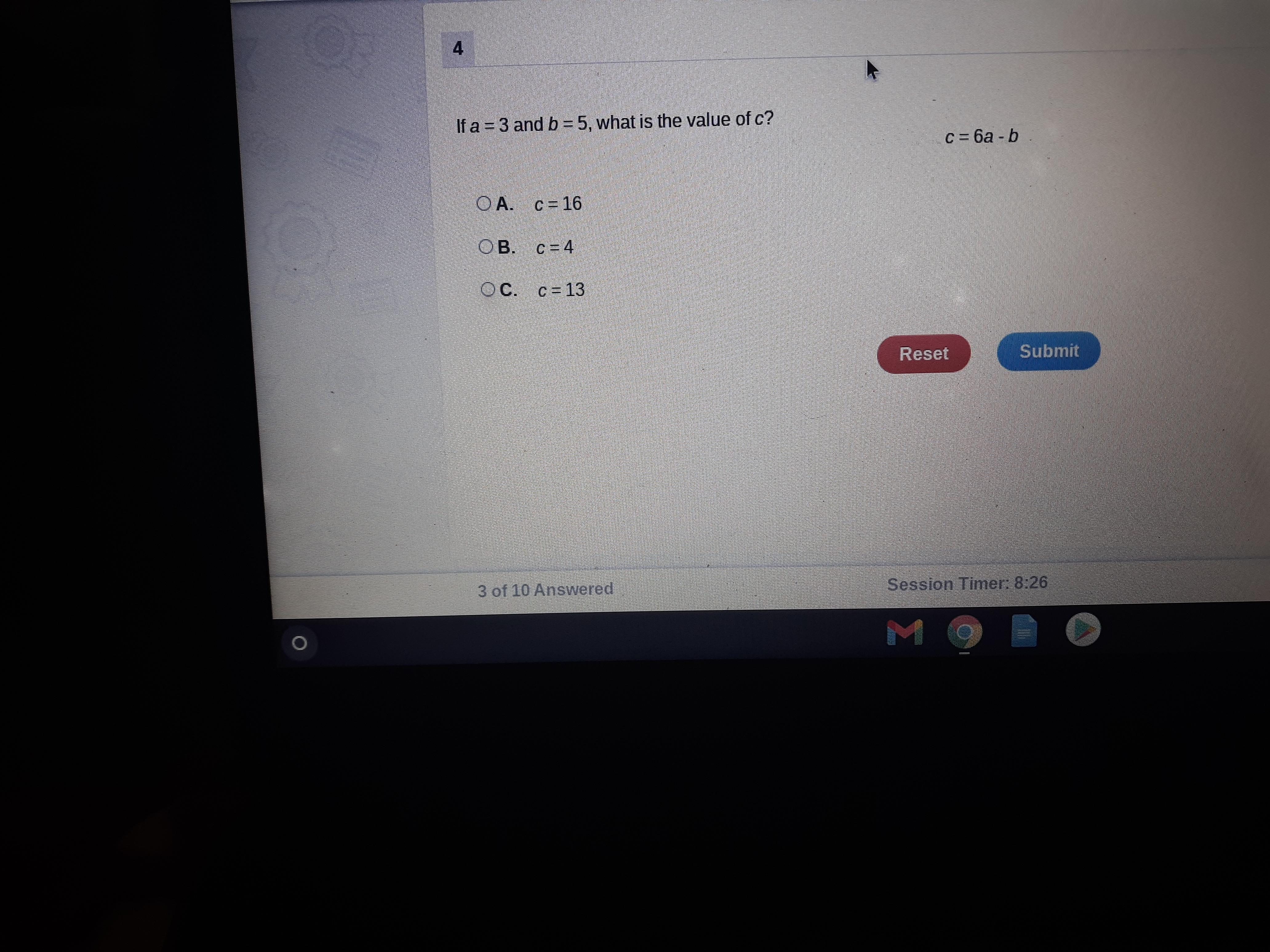
Answer:

Step-by-step explanation:

A sector is a portion of the circle that is bounded by 2 radii forming an angle at the center of the circle. If it is folded into a cone, the radius of the sector becomes the slant height of the cone. The length of the arc formed by the sector becomes the circumference of the circular base of the cone. Therefore, to calculate the

1) Base radius, we would apply the formula,

Circumference = 2πr

Circumference = length of arc = 125/360 × 2 × 3.14 × 18

= 39.25

Radius, r = 39.25/2 × 3.14 = 6.25 cm

2) Semi vertical height, we would apply Pythagoras Theorem with the slant height of the cone being the hypotenuse, the radius being the adjacent side and the slant height being the opposite side.

h² = 18² - 6.25² = 284.9375

h = √284.9375 = 16.88 cm

3) Volume = 1/3πr²h where h represents the vertical height

Volume = 1/3 × 3.14 × 6.25² × 16.88 = 690.15 cm³

\(\huge\underline\mathcal{\red{A}\blue{n}\pink{s}\purple{w}\orange{e}\green{r} -}\)

the question asks us to find the values of y.

the question can be solved as follows ~

\(\longrightarrow \: 5y {}^{2} - 17y = - 6\)

let's first convert the equation into its general formula , i.e. , ax² + bx + c = 0

\(\longrightarrow \: 5y {}^{2} - 17y + 6 = 0\)

using splitting the middle term , let's find out the factors of the given equation ~

\(\longrightarrow \: 5y {}^{2} - 15y - 2y + 6 = 0 \\ \\ \longrightarrow \: 5y \: (y - 3) - 2 \: (y - 3) = 0 \\ \\ \longrightarrow \: 5y - 2 = 0 \: \: \: or \: \: \: y - 3 = 0 \\ \\ \longrightarrow \:\boxed{ y = \frac{2}{5}} \: \: \: or \: \: \: \boxed{y = 3}\)

hope helpful ~

\( \: \: \: \: \: \: \: \: \: \: \: \: \purple\diamond{\boxed{\boxed{\boxed{\sf{{ \pink{ANSWER}}}}}}}\)

\(5y^2- 17y=-6\)

Move terms to the left side

\(5y^2- 17y=-6 \)

\(5y^2- 17y-(-6) = 0\)

Use the sum-product pattern

\(5y^2-17y+6=0\)

\(5y^2-2y-15y+6=0\)

Common factor from the two pairs

\((5y^2-2y)+(-15y+6) = 0\)

\(y(5y-2)-3(5y-2) = 0\)

Rewrite in factored form

\(y(5y-2)-3(5y-2) = 0\)

\((y-3)(5y-2) = 0\)

Create separate equations

\((y-3)(5y-2) = 0\)

\(y-3=0\)

\(5y-2=0\)

Solve :

Rearrange and isolate the variable to find each solution

\(y = 3\)

\(y = \frac{2}{5}\)

Answer:

DC = 16.5, CM = 16.5

Step-by-step explanation:

The centroid, C, would be the midpoint of DM if DM was a line between the midpoint of a side and it's opposite vertex. So DC and CM are half of DM. Hope this helps.

Answer:

Option B

Step-by-step explanation:

We are given the following system of equations -

\(\begin{bmatrix}-5x+2y-2z=26\\ 3x+5y+z=-22\\ -3x-5y-2z=21\end{bmatrix}\)

Now by Cramer's Rule, we would first write down the matrix of the coefficients , replacing each column with the answer column -

\(\begin{bmatrix}-5&2&-2\\ 3&5&1\\ -3&-5&-2\end{bmatrix}\) ,

\(\begin{bmatrix}26\\ -22\\ 21\end{bmatrix}\)

Replace each column of the coefficients shown at the top, with the answer column at the bottom respectively -

\(\begin{bmatrix}-5&2&26\\ 3&5&-22\\ -3&-5&21\end{bmatrix}\)

Now solve through Cramer's Rule -

x = Dx / D = - 6,

y = Dy / D = - 1,

z = Dz / D = 1

Solution = ( - 6, - 1, 1 ) = Option B

-5 x + 2 y - 2 z = 263 x + 5 y + z = -22 - 3 x - 5 y - 2 z = 21

Answer is x=-6,\:z=1,\:y=-1

According to the information, the missing number from the box is number 40.

To find the missing number of the table we must take into account different elements. In particular we must look at the totals and the columns and rows in which the empty space is. Once we identify the totals we can subtract the other values from the total and find the missing number in the table.

According to the above we can infer that the missing number is 40.

Learn more about numbers in: https://brainly.com/question/24908711
#SPJ1

Approximately 17.65% of Ana's salary is withheld for taxes.

To calculate the percentage of Ana's salary that is withheld for taxes, we need to determine the amount of tax withheld and then express it as a percentage of her net salary.

Number of hours worked per week (H) = 25 hours

Hourly wage (W) = $10

Net salary (S) = $212.50

Calculate the total earnings before taxes:

Total earnings = Hours worked * Hourly wage

Total earnings = 25 hours * $10/hour

Total earnings = $250

Determine the amount of tax withheld:

Tax withheld = Total earnings - Net salary

Tax withheld = $250 - $212.50

Tax withheld = $37.50

Calculate the percentage of salary withheld for taxes:

Percentage withheld = (Tax withheld / Net salary) * 100

Percentage withheld = ($37.50 / $212.50) * 100

Percentage withheld ≈ 17.65%

Therefore, approximately 17.65% of Ana's salary is withheld for taxes.

for such more question on percentage

https://brainly.com/question/24877689

#SPJ8

Answer:

-19

Step-by-step explanation:

18=-20-2b

18+20=-2b

38=-2b

b=-19

Answer:

$288

Step-by-step explanation:

10% of 240 is 240 / 10 = 24

24 X 2 = 48

240 + 48 = $288

Answer:

$288 ....brainliest appreciated pls

Step-by-step explanation:

20/100 × 240 = 48dollars

so...the selling price becomes 240+48 = $288

Answer:

The y intercept is (0,-22)

Step-by-step explanation:

The y intercept is the value when x =0

Y=5x-22

y = 5*0 -22

y = -22

The y intercept is (0,-22)

Answer:

According to the table, 97,825 females from a randomly selected population of 100,000 females live to the age of 38.

Step-by-step explanation:

Answer:

See image

Step-by-step explanation:

Plato

We can complete the blanks with the following ratios:

(7.5 mi/1) * (1 mi/ 5280 ft) * (400ft/1 yd) * (3 ft/1 ft) =33 flags

Since we do not need a flag at the starting line, then 32 flags will be required in total.

To solve the problem, we would first convert 400 yds to feet and miles.

To convert to feet, we multiply by 3. This gives us: 400 yd * 3 = 1200 feet.

To convert to miles, we would have 0.227 miles.

Now, we divide the entire race distance by the number of miles divisions.

This gives us:

7.5 mi /0.227 mi

= 33 flags

Learn more about miles-to-yards conversion here:

https://brainly.com/question/1609225

#SPJ1

Answer:

\(\frac{8}{15}\)

Step-by-step explanation:

Therefore, the answer is \(\frac{8}{15}\).

Answer:

-101

Step-by-step explanation:

Answer:

-101

Step-by-step explanation:

-12.8-88.2 is equal to -101

Answer: 36˚

Step-by-step explanation:

180 - 3x = 2x

180 = 5x

.: x = 36˚

Answer:

A

Step-by-step explanation:

slant height of the exagon = side/2 * √3 = 2.5√3 cm

area of the hexagon = (side * slant height)/2 * 6 = (5 * 2.5√3)/2 * 6 = 64,951905 cm^2

Volume of the prism = area of the hexagon * height = 974,278579 cm^3

Volume of the cylinder = radius^2 *  pi * height = 36 * pi * 15 = 1.696,460033 cm^3

volume of the kaleidoscope = 722,181454 cm^3

All of these options are equivalent and indicate that λ is an eigenvalue of the matrix A.

An eigenvector is a nonzero vector that when multiplied by a matrix, the result is a scalar multiple of the original vector. The scalar is called the eigenvalue. In other words, the eigenvector is a direction that is unchanged when the matrix is applied to it, but its magnitude may change.

If we assume that this vector is also an eigenvector, then we can write:

A x v = λ x v

where A is the square matrix, v is the nonzero vector in the null space, and λ is the eigenvalue. But we know that Av = 0 since v is in the null space. Thus, we have:

0 = λv

Since λ is nonzero (by definition of eigenvalue), we can divide both sides by λ:

0 / λ = v

This means that v must be the zero vector, which is a contradiction since we assumed v to be nonzero. Therefore, a vector in the nullspace cannot be an eigenvector.

Now, let's consider the options for what is equivalent to the statement that λ is an eigenvalue for a given square matrix.

There exists a nonzero vector v such that Av = λv

The determinant of A - λI (where I is the identity matrix) is equal to zero

The matrix A - λI is singular (i.e. its determinant is zero)

The rank of A - λI is less than the rank of A

To know more about matrix here.

https://brainly.com/question/28180105

#SPJ4

Answer:

what is this?

Step-by-step explanation:

if you elaborate I am more then happy to help

Answer:

.

Step-by-step explanation:

Answer:

c = 13

Step-by-step explanation:

c = 6(3) - 5

c = 13

Answer:

C. c=13

Step-by-step explanation:

This is how I figured it out:

1. I took the equation (c=6a-b) and I replaced the letters with the numbers given. (a=3 & b=5) so I got the new equation c=6(3)-5.

2. I used PEMDAS (parentheses, exponents, multiplication, division, addition and subtraction. Since we have multiplication and subtraction needed multiplication is shown before subtraction in PEMDAS so we would figure out 6(3) first which is equal to 18.

3. Now we have the new equation of c=18-5. Since subtraction is left we would take away 5 from 18 and now we have the final answer of 13. So the equation would now look like this: c=13. It's pretty obvious that c=13 that c has the value of 13.

I hope this helps:)

The values of f(x) for the given x - values rounded to 4 decimal places are 0.0078, 0.0078, 0.0020, 0.0020, 0.0019 and 0.0013 respectively

Given the function :

Substitute the given value of x to obtain the corresponding f(x) values :

x = -0.6

f(x) = (tanπ(-0.6))/7(-0.6) = 0.0078358

x = -0.51

f(x) = (tanπ(-0.51))/7(-0.51) = 0.0078350

x = -0.501

f(x) = (tanπ(-0.501))/7(-0.501) = 0.001967

x = -0.5

f(x) = (tanπ(-0.5))/7(-0.5) = 0.001959

x = -0.4999

f(x) = (tanπ(-0.4999))/7(-0.4999) = 0.001958

x = 0.499

f(x) = (tanπ(-0.499))/7(-0.499) = 0.001951

x = -0.49

f(x) = (tanπ(-0.49))/7(-0.49) = 0.00188

x = -0.4

f(x) = (tanπ(-0.4))/7(-0.4) = 0.00125

Therefore, values which complete the table are 0.0078, 0.0078, 0.0020, 0.0020, 0.0019 and 0.0013

Learn more on functions : https://brainly.com/question/12634120

#SPJ1

Using DeMoivre’s theorem, the answer in regular form would be (5 + 5√3i)⁷ = -5000000 + 8660254.03i

The De Moivre's Theorem is used to simplify the computation of powers and roots of complex numbers and is used in together with polar form.

Convert the complex number to polar form. The polar form of a complex number is z = r(cos θ + isin θ),

r = |z|  magnitude of z

it becomes

r = √((5)² + (5√3)²) = 10

θ = arg(z) is the argument of z.

θ = atan2(b, a) = atan2(5√3, 5) = π/3

(5 + 5√3i) = 10 × (cos π/3 + i sin π/3)

De Moivre's theorem to raise the complex number to the 7th power

(5 + 5√3i)⁷

= 10⁷× (cos 7π/3 + i sin 7π/3)

= 10⁷ × (cos 2π/3 + i sin 2π/3)

Convert this back to rectangular form:

Real part = r cos θ = 10⁷× cos (2π/3) = -5000000

Imaginary part = r sin θ = 10⁷ × sin (2π/3) = 5000000√3 = 8660254.03i

∴  (5 + 5√3i)⁷ = -5000000 + 8660254.03i

Find more exercises on De Moivre's Theorem ;

https://brainly.com/question/28999678

#SPJ1

Answer:10^7 (1/2 - √3/2 i)

Step-by-step explanation:

To use DeMoivre's theorem, we first need to write the number in polar form. Let's find the magnitude and argument of the number:

Magnitude:

|5 + 5√(3i)| = √(5^2 + (5√3)^2) = √(25 + 75) = √100 = 10

Argument:

arg(5 + 5√(3i)) = tan^(-1)(√3) = π/3

So the number can be written in polar form as:

5 + 5√(3i) = 10(cos(π/3) + i sin(π/3))

Now we can use DeMoivre's theorem:

(5 + 5√(3i))^7 = 10^7 (cos(7π/3) + i sin(7π/3))

To simplify, we need to find the cosine and sine of 7π/3:

cos(7π/3) = cos(π/3) = 1/2

sin(7π/3) = -sin(π/3) = -√3/2

Explanation:

So the final answer in rectangular form is:

10^7 (1/2 - √3/2 i)

Answer:

4:25 I think

Step-by-step explanation:

just added them all up I don't know if that's what you needed yho

Answer:

15:85 or 4:25

Step-by-step explanation:

jfhfjfjfjfjfndndndndndjdjfjfnnfjfjdjfjfjf

The area of the shaded portion in the equilateral triangle with sides 6 is 9√3 - 36π.

To find the area of the shaded portion in the equilateral triangle, we need to determine the area of the three arcs and subtract it from the area of the equilateral triangle.

First, let's find the area of one arc. Each arc has a radius equal to the length of the side of the equilateral triangle, which is 6. The formula for the area of a sector is A = (θ/360)πr², where θ is the central angle in degrees.

In an equilateral triangle, each interior angle measures 60 degrees, so the central angle of the arc is 120 degrees (360 degrees divided by 3). Plugging these values into the formula, we get A_arc = (120/360)π(6)² = (1/3)π(6)² = 12π.

Since there are three identical arcs, the total area of the arcs is 3 times the area of one arc, which is 3(12π) = 36π.

Now, let's find the area of the equilateral triangle. The formula for the area of an equilateral triangle is A_triangle = (√3/4)s², where s is the length of a side.

Plugging in the value of the side length, we have A_triangle = (√3/4)(6)² = (√3/4)(36) = 9√3.

Finally, we subtract the area of the arcs from the area of the equilateral triangle to find the shaded portion's area: A_shaded = A_triangle - A_arc = 9√3 - 36π.

For more such questions on triangle

https://brainly.com/question/1058720

#SPJ8

A scatter plot shows the correlation between 2 variables.

If the correlation is positive, the variables move in the same direction.

If the correlation is negative, the variables move in opposite direction.

To answer this question, observe the image below:

As can be observed, when driver age increases, the distance decreases.

So, the correlation is negative.

Answer: B) negative.

Answer:

6x+4y+3xy-2x+2y+2xy

4x+2y+xy

this is the answer

Step-by-step explanation:

4x+2y+xy answer

hope this will help you

Answer: y=(-5/3)x+8

Step-by-step explanation: earrange 5x+3y=6 in slope intercept form

y=mx=b

5x+3y=6

     3y=6-5x

       y=2-(5x)/3

then slope for a line parallel is -5/3

Use point slope form y-y1=m(x-x1)

plug un values of (x,y) = (6,-2)

and m=-5/3

y-y1=m(x-x1)

y-(-2)=(-5/3)(x-6)

y+2=(-5/3)x+10

y=(-5/3)x+10-2

y=(-5/3)x+8 <-- solution