Sandra takes 28 hours to finish a rectangular tapestry. If she works at the
same rate, how long will it take her to finish a bigger rectangular tapestry
that is 50% longer and 30% wider? Give your answer correct to the
nearest hour.

Answer:

3. 18 4. 54 5. 1 1/4 6. 6 divided by 1/4 which is 24

Step-by-step explanation:

I am pretty sure :)

The Longest Increasing Subsequence (LIS) problem is a classic problem in dynamic programming. Given a sequence of numbers, the problem is to find the longest subsequence in which the numbers are in increasing order. For example, given the sequence {3, 1, 5, 2, 4}, the longest increasing subsequence is {1, 2, 4}, which has length 3.

The LIS problem can be solved using dynamic programming by defining an array to store the length of the longest increasing subsequence that ends at each position in the sequence. The array is initialized to 1, and then for each position i in the sequence, the length of the longest increasing subsequence that ends at i is calculated by finding the maximum length of any subsequence that ends at a position j < i and has a smaller value than the value at i. The final solution is the maximum length of any subsequence in the array.

Find out more  about dynamic programming

brainly.com/question/29809157

#SPJ4

Answer:

Step-by-step explanation:

The height of the trapezoid needs to be 30/11 units in order for the trapezoid to have area 30.

To find the height of the trapezoid, we can use the formula for the area of a trapezoid, which is:

A = (1/2)h(b1 + b2)

where A is the area of the trapezoid, h is the height, b1 and b2 are the lengths of the parallel bases.

We know that the lengths of the parallel bases are 8 and 14, and we want the area to be 30. Substituting these values into the formula, we get:

30 = (1/2)h(8 + 14)

Simplifying the right-hand side, we get:

30 = 11h

Dividing both sides by 11, we get:

h = 30/11

Therefore, the height of the trapezoid needs to be 30/11 units in order for the trapezoid to have area 30.

To see why this works, we can visualize the trapezoid as a rectangle with a smaller right triangle on top. The height of the rectangle is equal to the height of the trapezoid, and the width is equal to the average of the lengths of the bases, which is (8+14)/2 = 11. The area of the rectangle is therefore 11h, and the area of the triangle on top is (1/2)bh, where b is the difference between the lengths of the bases, which is 14-8 = 6. The total area of the trapezoid is the sum of the area of the rectangle and the area of the triangle, which is:

A = 11h + (1/2)(6)(h) = 11.5h

Setting this equal to 30 and solving for h, we get the same result as before:

11.5h = 30

h = 30/11

Therefore, the height of the trapezoid needs to be 30/11 units in order for the trapezoid to have area 30.

To know more about area of a trapezoid refer here:

https://brainly.com/question/21025771

#SPJ11

The trigonometric ratios with respect to angle A are given as follows:

The three trigonometric ratios are the sine, the cosine and the tangent, and they are defined as follows:

The hypotenuse is of 37, and the sides relative to angle A are given as follows:

Hence the trigonometric ratios are given as follows:

More can be learned about trigonometric ratios at brainly.com/question/24349828

#SPJ1

Answer: 86 ÷ x or 86 / x

Step-by-step explanation:

A quotient is a number that results when one number is divided by another.

Therefore, in order to get the quotient, numbers or terms should process division which the final answer would be quotient.

In the process, [÷ ] or [/] the division signs shall be applied.

The quotient of 86 and x represents 86 divided by x, which the final result would be \(\boxed {86/x}\)

Hope this helps!! :)

Please let me know if you have any questions

I believe the answer you are looking for is simply just 86÷x or 86/x.

Answer:

1) -2

2) 8/3

3) 1/2

4) -1/2

5) 5/9

6) -4

Step-by-step explanation:

The slope formula is:

rise/run

The difference in the Y  value is the rise and the difference in the x is the run.

for number 1, you would do

8-4/1-3

4/-2

slope = -2

and so on

Answer:

D) The same as

Step-by-step explanation:

both 4x and 2x have x at the end

x equals x

Answer:

D.same as  cause both the 4 and the 2 have x and x do equal x

Step-by-step explanation:

The disc jockey could use a Monte Carlo simulation to estimate the probability that the next three songs are all rock songs.

In this simulation, she would randomly select a rock or pop song for each of the three slots, and then repeat this process many times (e.g. 10,000 times). She could then count the number of times that all three songs were rock songs, and divide this by the total number of simulations to get an estimate of the probability.

To estimate the probability that the next three songs are all rock songs, the disc jockey could use the following simulation design:
1. Assign a number to each rock and pop song, ensuring that both genres have equal numbers.
2. Use a random number generator to select three numbers corresponding to the songs.
3. Record the genres of the chosen songs and note if all three are rock songs.
4. Repeat the simulation process multiple times (e.g., 1000 times) to obtain a larger sample.
5. Calculate the probability by dividing the number of times all three selected songs were rock songs by the total number of simulations performed.
This simulation design will help estimate the probability of the next three songs being rock songs by accounting for the equal number of rock and pop songs in the selection pool.

To learn more about probability visit;

https://brainly.com/question/30034780

#SPJ11

The value of the double integral is  \(I = \int\limits^{\pi/2}_{\pi/4} \int\limits^{3/sin0}_{r=0} r^{2}cos0drd0\).

Let z* be the common (finite) optimal value of P and D.

Given integral is

\(I = \int\limits^3_{y = 0} \int\limits^y_{x=0} {x} \, dxdy\)

The region of integration lies between

y = 0, y = 3, x = 0 & x = y

Let x = rcosθ, y = rsinθ,

\(x^{2} +y^{2}= r^{2}\)

At y = 3, rsinθ = 3

Thus r varies from 0 to 3/sinθ

θ varies from π/4 to π/2

Now, dxdy ----> rdrdθ

Therefore,

\(I = \int\limits^{\pi/2}_{\pi/4} \int\limits^{3/sin0}_{r=0} r^{2}cos0drd0\)

Hence the answer is The value of the double integral is  \(I = \int\limits^{\pi/2}_{\pi/4} \int\limits^{3/sin0}_{r=0} r^{2}cos0drd0\).

To learn more about double integral click here https://brainly.com/question/12481861

#SPJ4

we need to find the parametric equations for the tangent line at the point (cos(56π),sin(56π),56π) on the curve x = cos(t), y = sin(t), z = t.

To find the tangent line, we need to calculate the derivatives of x(t), y(t), and z(t) with respect to t. The derivatives give us the slopes of the tangent line in each direction. Then, we can use the point-slope form of a line to obtain the parametric equations.

The derivative of x(t) is -sin(t), the derivative of y(t) is cos(t), and the derivative of z(t) is 1. Using these derivatives, we can construct the parametric equations for the tangent line passing through the given point.

To know more about tangent line here: brainly.com/question/31617205

#SPJ11

The best interpretation of  P(3) = 12 is that the probability of 3 is 12

Probability is simply described as an important branch of mathematics that concerns numerical descriptions of the likelihood  of the occurance of an event the proposition of how true it is.

The probability of an event is a number that must be between 0 and 1.

Given that;

Note that the analysis of events that is being governed by probability is known as statistics.

The types of probability are;

Hence, P(3) = 12 is  the probability of 3 is 12

Learn more about probability here:

https://brainly.com/question/24756209

#SPJ1

Answer:

(c) The equation, y = -3x + 100, represents the Model S tank.

(f) The Model T tank drains the fastest at 3.5 gallons per minute.

Step-by-step explanation:

Given

See attachment for models S and T

First, we calculate the equation of both models

Model S

\((x_1,y_1) = (0,100)\\\\(x_2,y_2) = (6,82)\)

Calculate drainage rate (m)

\(m = \frac{y_2 - y_1}{x_2 -x_1}\)

\(m = \frac{82-100}{6-0}\)

\(m = \frac{-18}{6}\)

\(m = -3\) -- This implies that model S drains at 3 gallons per minutes

The equation is:

\(y = m(x - x_1) + y_1\)

\(y = -3(x - 0)+100\)

\(y = -3(x)+100\)

\(y = -3x+100\)

Model T

\((x_1,y_1) = (0,100)\\\\(x_2,y_2) = (4,86)\)

Calculate drainage rate (m)

\(m = \frac{y_2 - y_1}{x_2 -x_1}\)

\(m = \frac{86-100}{4-0}\)

\(m = \frac{-14}{4}\)

\(m = -3.5\) -- This implies that model T drains at 3.5 gallons per minutes

The equation is:

\(y = m(x - x_1) + y_1\)

\(y = -3.5(x - 0)+100\)

\(y = -3.5(x)+100\)

\(y = -3.5x+100\)

From the calculations above, the following options are true:

(c) and (f)

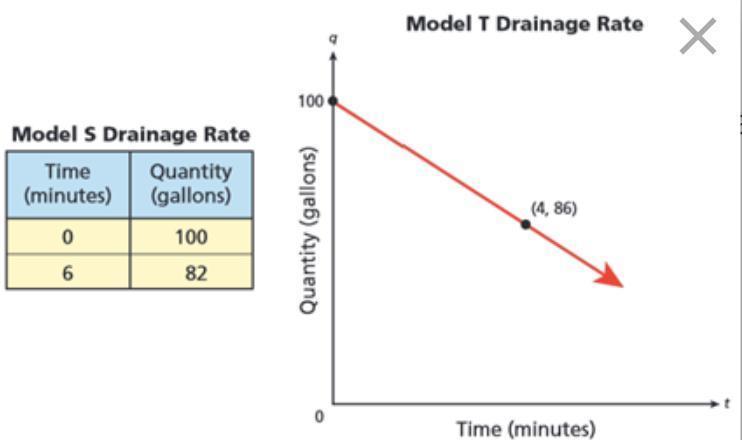
It is required to find which statements are true.

The statements that are true are

The equation, y = -3x + 100, represents the Model S tank.

The Model T tank drains the fastest at 3.5 gallons per minute.

Equation of a line is

\(y=mx+c\)

where,

\(y=\text{Gallons of water left}\)

\(x=\text{Minutes passed}\)

\(m=\text{Slope}=\dfrac{\Delta y}{\Delta x}\)

\(c=\text{Y intercept}\)

The equation of the line for model S is

\(y-100=\dfrac{82-100}{6-0}(x-0)\\\Rightarrow y-100=-3x\\\Rightarrow y=-3x+100\)

The option C is true.

The equation of the line for model T is

\(y-100=\dfrac{86-100}{4-0}(x-0)\\\Rightarrow y-100=-3.5x\\\Rightarrow y=-3.5x+100\)

The slope or rate of drain is 3.5 gallons per minute.

So, option F is true.

Learn more:

https://brainly.com/question/18011570?referrer=searchResults

The family of functions P = C1e^t / (1 + C1e^t) is a solution to the differential equation dP/dt = P(1 - P) on an appropriate interval of definition.

In the first paragraph, we summarize that the family of functions P = C1e^t / (1 + C1e^t) is a solution to the differential equation dP/dt = P(1 - P). This equation represents the rate of change of the variable P with respect to time t, and the solution provides a relationship between P and t. In the second paragraph, we explain why this family of functions satisfies the given differential equation.

To verify the solution, we can substitute P = C1e^t / (1 + C1e^t) into the differential equation dP/dt = P(1 - P) and see if both sides are equal. Taking the derivative of P with respect to t, we have:

dP/dt = [d/dt (C1e^t / (1 + C1e^t))] = C1e^t(1 + C1e^t) - C1e^t(1 - C1e^t) / (1 + C1e^t)^2

      = C1e^t + C1e^(2t) - C1e^t + C1e^(2t) / (1 + C1e^t)^2

      = 2C1e^(2t) / (1 + C1e^t)^2.

On the other hand, evaluating P(1 - P), we get:

P(1 - P) = (C1e^t / (1 + C1e^t)) * (1 - C1e^t / (1 + C1e^t))

        = (C1e^t / (1 + C1e^t)) * (1 - C1e^t + C1e^t / (1 + C1e^t))

        = (C1e^t - C1e^(2t) + C1e^t) / (1 + C1e^t)

        = (2C1e^t - C1e^(2t)) / (1 + C1e^t)

        = 2C1e^t / (1 + C1e^t) - C1e^(2t) / (1 + C1e^t).

Comparing the two sides, we see that dP/dt = P(1 - P), which means the family of functions P = C1e^t / (1 + C1e^t) is indeed a solution to the given differential equation.

Learn more about differential equation here:

https://brainly.com/question/25731911

#SPJ11

Finally, we need to subtract one-half the original number, which is $\frac{x}{2}$. So the final expression is:$$\frac{x+100}{2} - \frac{x}{2} = 50$$

1. Let's call the original number x.
2. Double the number: 2x
3. Add 200: 2x + 200
4. Divide the answer by 4: (2x + 200) / 4
5. Subtract one-half the original number: ((2x + 200) / 4) - (x / 2)

Now let's simplify the expression:

((2x + 200) / 4) - (x / 2)

= (2x/4 + 200/4) - (x / 2)

= (x/2 + 50) - (x / 2)

= x/2 - x/2 + 50

= 0 + 50

So, the value of the result is 50.

To know more about final expression visit:

https://brainly.com/question/29264271

#SPJ11

The rate at which the area of the triangle is increasing when the angle between the sides of fixed lengths is π/3 is 0.3 m²/s.

If the lengths a and b for two sides of the triangle, as well as the included angle θ, are known, the area of a triangle can be calculated using the sine formula.

\(\text { Area }=\frac{1}{2} a b \sin \theta\)

Now, according to the question;

The two sides of the triangle are given;

Let a = 4m and b = 5m.

Let θ = π/3. be the angle between the two sides;

Then,

Differentiate the area with respect to time (as rate of change of area)

\(\begin{aligned}\frac{\mathrm{d} A}{\mathrm{~d} t}=\frac{\mathrm{d}}{\mathrm{d} t} \frac{1}{2} a b \sin \theta &=\frac{1}{2} * 4 * 5 * \frac{\mathrm{d}(\sin \theta)}{\mathrm{d} \theta} \cdot \frac{\mathrm{d} \theta}{\mathrm{d} t} \\&=10 *(\cos \theta) * 0.06 \frac{\mathrm{m}^{2}}{\mathrm{~s}}=0.6 \cos (\pi / 3) \frac{\mathrm{m}^{2}}{\mathrm{~s}} \\&=0.6 * 0.5 \frac{\mathrm{m}^{2}}{\mathrm{~s}}=0.3 \frac{\mathrm{m}^{2}}{\mathrm{~s}}\end{aligned}\)

Therefore, the area of the triangle as a function of angle is 0.3 m²/s.

To know more about rate of change of area, here

https://brainly.com/question/17203328

#SPJ4

The complete question is-

Two sides of a triangle are 4m and 5 m in length and the angle between them is increasing at a rate of 0.06 rad/sec. Find the rate at which the area of the triangle is increasing when the angle between the sides of fixed lengths is π/3.

The dot plot of the data values is added as an attachment

From the question, we have the following parameters that can be used in our computation:

85,88,75,100,90,90,88,72,72,79,88,85

Next, we create a frequency table

So, we have

Values   Frequency

72             2

75             1

79             1

85            2

88            3

90           2

100          1

Total      12

Using the frequency table above, we create the dot plot

See attachment for the dot plot

Read more about dot plot

https://brainly.com/question/30117279

#SPJ1

The percentage of the data values in the box-and-whiskers plot, that are greater than or equal to 92, which is the 75th percentile, based on the five number summary, are 25 percent of the data.

The five number summary of a box-and-whiskers plot are value of the minimum, the first quartile, the median, the third quartile and the maximum value of the set of data.

Please find attached the possible box-and-whiskers plot in the question, obtained from a similar question on the internet

The five number summary from the box-and-whiskers plot are;

Minimum value = 82

The first quartile or the 25th percentile = 87

The median, second quartile or the 50th percentile = 90

The third quartile or the 75th percentile = 92

The value 92 on the data represents the 75th percentile, therefore, the percentage of the data that are greater than or equal to 92 are; 100 - 75 = 25 percent

Learn more on box-and-whiskers plots here: https://brainly.com/question/973515

#SPJ1

Answer:

The constant of variation is k=5

Step-by-step explanation:

Proportions

A direct proportion is a relation between variables where their ratio is a constant value. This means that if y and x are proportional, then:

\(y=k\cdot x\)

Where k is the constant of proportionality.

We know R varies directly with S. Their relationship is:

\(R=k\cdot S\)

We also have when S=16, R=80. Thus:

\(80=k\cdot 16\)

Solving for k:

\(k=80/16=5\)

The constant of variation is k=5

Answer:

No

Step-by-step explanation:

\(5^{2} = 25\\9^{2} = 81\\11^{2} = 121\\25 + 81 = 106\)

therefore it doesn't coenide with pythagorian theorem

The total cost of power generation for a specific load demand can be calculated by optimally allocating the load demand to each unit based on their power output limits. The allocation is done in a way that minimizes the overall cost while meeting the load demand.

In the given power system depicted in Figure 1, there are three units that are always running. Each unit has specific characteristics regarding their minimum power output (Pmin), maximum power output (Pmax), and incremental cost (Ci). Let's discuss the characteristics of each unit and calculate the total cost of power generation for a given load demand.

Unit 1:

Pmin = 200 MW

Pmax = 500 MW

Ci = $50/MWh

Unit 2:

Pmin = 150 MW

Pmax = 400 MW

Ci = $40/MWh

Unit 3:

Pmin = 100 MW

Pmax = 300 MW

Ci = $30/MWh

To calculate the total cost of power generation for a given load demand, we need to determine the optimal power output for each unit. We start by considering the units with the lowest incremental cost first.

Suppose the load demand is D MW. We allocate the load demand to the units as follows:

Step 1: Check if Unit 1 can meet the load demand within its power range. If yes, allocate the load demand to Unit 1 and calculate the cost:

Cost1 = Ci * P1, where P1 is the power output of Unit 1.

Step 2: If there is still remaining load demand, allocate it to Unit 2:

Cost2 = Ci * P2, where P2 is the power output of Unit 2.

Step 3: If there is still remaining load demand, allocate it to Unit 3:

Cost3 = Ci * P3, where P3 is the power output of Unit 3.

Finally, the total cost of power generation, Cost_total, is the sum of Cost1, Cost2, and Cost3:

Cost_total = Cost1 + Cost2 + Cost3

To find the optimal power output for each unit, we consider the load demand and compare it to the minimum and maximum power output limits for each unit. The power allocation is based on meeting the load demand while minimizing the overall cost of power generation.

In summary, given the characteristics of the three units in the power system (Pmin, Pmax, and Ci), the total cost of power generation for a specific load demand can be calculated by optimally allocating the load demand to each unit based on their power output limits. The allocation is done in a way that minimizes the overall cost while meeting the load demand.

Learn more about demand here

https://brainly.com/question/14274996

#SPJ11

In the inpatient setting, a CPT code (Current Procedural Terminology) would typically be assigned by the hospital for a procedure code to accurately bill for the services provided during the patient's stay.

This code is used to describe the specific medical service or procedure performed, such as a surgery or diagnostic test. It is important for hospitals to accurately assign CPT codes to ensure proper billing and reimbursement for the services provided. Additionally, the use of standardized CPT codes helps to facilitate communication and record-keeping across different healthcare providers and facilities.

Visit here to learn more about Current Procedural Terminology brainly.com/question/28296339

#SPJ11

Answer:

Step-by-step explanation:

\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\\\d=\sqrt{(1-11)^2+(3-10)^2}=\sqrt{(-10)^2+(-7)^2}=\sqrt{149}\\\\d=12.2065...\approx12.2\)

Using the equation for equilibrium output, Y = C + I, we can solve for the initial output level when I = 75:
Y = C + I

Y = 550(0.8Y) + 75
Y = 440Y + 75
Y = 75/(1-440)
Y = 132.35
So the initial equilibrium output is 132.35.
Now, if investment increases by 100, the new level of investment would be I = 75 + 100 = 175. Plugging this into the equation for equilibrium output, we get:
Y = C + I
Y = 550(0.8Y) + 175
Y = 440Y + 175
Y = 175/(1-440)
Y = 313.72
So the new equilibrium output is 313.72. The increase in equilibrium output is the difference between the new and initial equilibrium output levels:
ΔY = 313.72 - 132.35 = 181.37
Therefore, if investment increases by 100, the equilibrium output increases by a total of 181.37.
Based on the information provided, we have a simple economy with no government or foreign sector. The consumption function is given as C = 550 + 0.8Y, and the initial investment (I) is 75. If the investment increases by 100, we need to find the increase in equilibrium output.
In this economy, the equilibrium output (Y) is determined by the equation Y = C + I. After the investment increase, the new investment (I') is 175 (75 + 100). Now, we can find the new equilibrium output (Y') using the updated equation Y' = C + I':
Y' = 550 + 0.8Y' + 175
To solve for Y', we can rearrange the equation:
0.2Y' = 725
Y' = 3625
Now, to find the increase in equilibrium output, we subtract the initial output (Y) from the new output (Y'):
Increase in output = Y' - Y = 3625 - 3250 = 375
So, the equilibrium output increases by a total of 375 when the investment increases by 100.

To know more about equilibrium visit:

https://brainly.com/question/30694482

#SPJ11

Answer:

x² + (y + 3)² = 25

Step-by-step explanation:

the centre (C) of the circle is at the midpoint of the diameter.

using the midpoint formula

midpoint = ( \(\frac{x_{1}+x_{2} }{2}\) , \(\frac{y_{1}+y_{2} }{2}\) )

with (x₁, y₁ ) = P (3, 1 ) and (x₂, y₂ ) = Q (- 3, - 7 )

C = ( \(\frac{3-3}{2}\) , \(\frac{1-7}{2}\) ) = ( \(\frac{0}{2}\) , \(\frac{-6}{2}\) ) = (0, - 3 )

the radius r is the distance from the centre to either P or Q

using the distance formula

r = \(\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\)

with (x₁, y₁ ) = C (0, - 3 ) and (x₂, y₂ ) = P (3, 1 )

r = \(\sqrt{(3-0)^2+(1-(-3)^2}\)  

 = \(\sqrt{3^2+(1+3)^2}\)

 = \(\sqrt{3^2+4^2}\)

 = \(\sqrt{9+16}\)

 = \(\sqrt{25}\)

 = 5

the equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k ) are the coordinates of the centre and r is the radius

here (h, k ) = (0, - 3 ) and r = 5 , then

(x - 0 )² + (y - (- 3) )² = 5² , that is

x² + (y + 3)² = 25

Answer:

It decreases $2 with each lunch bought.

Step-by-step explanation:

It decreases by $16 from 8 lunches. I took the $16 and divided it by the 8 lunches to get $2 each lunch.

(a) Find the dual of the LP.Primal problem isminimize \($b_1y_1+C_1x_1+...+C_nx_n$\) subject to \($a_{11}x_1+a_{12}x_2+...+a_{1n}x_n \leq\) \(b_1$...$a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n \leq b_m$ and $x_1, x_2,\)..., x_n\(\geq 0$\)

Let us find the dual of the above primal problem.

Dual problem ismaximize \($b_1y_1+...+b_my_m$\)subject to \($a_{11}y_1+a_{21}y_2+...+a_{m1}y_m \leq\)\(C_1$...$a_{1n}y_1+a_{2n}y_2+...+a_{mn}y_m \leq C_n$\)

and\($y_1, y_2, ..., y_m \geq 0$\)

(b) Find the standard form of the LP and dual.Standard form of the primal problem isminimize \($b_1y_1+C_1x_1+...+C_nx_n$\)subject to \($a_{11}x_1+a_{12}x_2+...+a_{1n}x_n +s_1 = b_1$...$a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n +s_m = b_m$\) and\($x_1, x_2, ..., x_n, s_1, s_2, ..., s_m \geq 0$\)

Standard form of the dual problem ismaximize \($b_1y_1+...+b_my_m$\)subject to \($a_{11}y_1+a_{21}y_2+...+a_{m1}y_m \leq 0$...$a_{1n}y\)

To know more about isminimize visit:

https://brainly.com/question/32370699

#SPJ11

The function satisfies the following properties:

(a) satisfies (u,v) = (v,u)

(c) satisfies (u, v+w) = (u,v) + (u,w)

(e) satisfies c(u,v) = (cu,v)

(g) satisfies (v,v) >= 0 and (v,v) = 0 if and only if v = 0

(a) The function satisfies (u,v) = (v,u) because the order of the elements in the inner product does not affect the result.

(c) The function satisfies (u, v+w) = (u,v) + (u,w) because it follows the distributive property of addition.

(e) The function satisfies c(u,v) = (cu,v) because it follows the property of scalar multiplication.

(g) The function satisfies (v,v) >= 0 and (v,v) = 0 if and only if v = 0 because it fulfills the requirements for a non-negative value for the inner product and the condition for the inner product to be zero only when the vector is the zero vector.

To know more about function refer here:

https://brainly.com/question/31062578

#SPJ11