Samantha has 146 ft of yarn. She wants to cut the yarn into equal pieces to give her 18 students. How much yarn will she give each student?
Answers
Answer
answers is 267 bits oof yard
Step-by-step explanation:
Answer:
146 divided into 18 would be 8.11111111111.. and so on.
Step-by-step explanation:
Hope that helps :)
Related Questions
The area of a triangle is 60 cm2. Its base measures 5 cm. What is the triangle's
height on this base?
possible answers:
7.75 cm approximately
12 cm
24 cm
150 cm
Answers
Answer:
24
Step-by-step explanation:
Answer:
h = 24 cm
Step-by-step explanation:
Area = 1/2 b * h
b = 5 cm
Area = 60 cm^2
60 = 1/2 * 5 * h Multiply both sides by 2
60*2 = 2*1/2 * 5 * h
120 = 5 h Divide by 5
24 = h
[3x (4.6÷2)] +14.1 =
Answers
Answer:
21
Step-by-step explanation:
PEMDAS : Parenthesis, Exponent, Multiplication/Division, Addition/Subtraction.
First, we want to deal with the parenthesis within the parenthesis.
(4.6/2) = 2.3
Rewrite it into the equation.
[3 * 2.3] + 14.1 = ?
Now, do the work in the parenthesis again.
[6.9] + 14.1 = ?
There isn't anymore parenthesis, exponents, or multiplication/division, so we move onto addition now and add both terms.
6.9 + 14.1 = 21
? = 21
The answer is 21.
Find the missing side lengths, put answer as radical in simplest form
Look at picture for reference

Answers
The value of the missing side lengths x and y are 5√2 and 5 respectively.
What is the value of side length x and y?The figure in the image is a right triangle.
Angle θ = 45 degree
Hypotenuse = x
Opposite to angle θ = y
Adjacent to angle θ = 5
To solve for side x and side y, we use the trigonometric ratio.
Note that:
Cosine = adjacent / hypotenuse
tangent = opposite / adjacent
Solving for x:
Cosine = adjacent / hypotenuse
Plug in the values
cos( 45 ) = 5/x
x = 5 / cos( 45 )
x = 5√2
Solving for side y:
tangent = opposite / adjacent
Plug in the values
tan( 45 ) = y/5
y = tan( 45 ) × 5
y = 5
Therefore, the value of side length x is 5 units.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
A manufacturer of computer memory chips produces chips in lots of 1000. If nothing has gone wrong in the manufacturing process, at most 7 chips each lot would be defective, but if something does go wrong, there could be far more defective chips. If something goes wrong with a given lot, they discard the entire lot. It would be prohibitively expensive to test every chip in every lot, so they want to make the decision of whether or not to discard a given lot on the basis of the number of defective chips in a simple random sample. They decide they can afford to test 100 chips from each lot. You are hired as their statistician.
There is a tradeoff between the cost of eroneously discarding a good lot, and the cost of warranty claims if a bad lot is sold. The next few problems refer to this scenario.
Problem 8. (Continues previous problem.) A type I error occurs if (Q12)
Problem 9. (Continues previous problem.) A type II error occurs if (Q13)
Problem 10. (Continues previous problem.) Under the null hypothesis, the number of defective chips in a simple random sample of size 100 has a (Q14) distribution, with parameters (Q15)
Problem 11. (Continues previous problem.) To have a chance of at most 2% of discarding a lot given that the lot is good, the test should reject if the number of defectives in the sample of size 100 is greater than or equal to (Q16)
Problem 12. (Continues previous problem.) In that case, the chance of rejecting the lot if it really has 50 defective chips is (Q17)
Problem 13. (Continues previous problem.) In the long run, the fraction of lots with 7 defectives that will get discarded erroneously by this test is (Q18)
Problem 14. (Continues previous problem.) The smallest number of defectives in the lot for which this test has at least a 98% chance of correctly detecting that the lot was bad is (Q19)
(Continues previous problem.) Suppose that whether or not a lot is good is random, that the long-run fraction of lots that are good is 95%, and that whether each lot is good is independent of whether any other lot or lots are good. Assume that the sample drawn from a lot is independent of whether the lot is good or bad. To simplify the problem even more, assume that good lots contain exactly 7 defective chips, and that bad lots contain exactly 50 defective chips.
Problem 15. (Continues previous problem.) The number of lots the manufacturer has to produce to get one good lot that is not rejected by the test has a (Q20) distribution, with parameters (Q21)
Problem 16. (Continues previous problem.) The expected number of lots the manufacturer must make to get one good lot that is not rejected by the test is (Q22)
Problem 17. (Continues previous problem.) With this test and this mix of good and bad lots, among the lots that pass the test, the long-run fraction of lots that are actually bad is (Q23)
Answers
Step-by-step explanation:
A manufacturer of computer memory chips produces chips in lots of 1000. If nothing has gone wrong in the manufacturing process, at most 7 chips each lot would be defective, but if something does go wrong, there could be far more defective chips. If something goes wrong with a given lot, they discard the entire lot. It would be prohibitively expensive to test every chip in every lot, so they want to make the decision of whether or not to discard a given lot on the basis of the number of defective chips in a simple random sample. They decide they can afford to test 100 chips from each lot. You are hired as their statistician.
There is a tradeoff between the cost of eroneously discarding a good lot, and the cost of warranty claims if a bad lot is sold. The next few problems refer to this scenario.
Problem 8. (Continues previous problem.) A type I error occurs if (Q12)
Problem 9. (Continues previous problem.) A type II error occurs if (Q13)
Problem 10. (Continues previous problem.) Under the null hypothesis, the number of defective chips in a simple random sample of size 100 has a (Q14) distribution, with parameters (Q15)
Problem 11. (Continues previous problem.) To have a chance of at most 2% of discarding a lot given that the lot is good, the test should reject if the number of defectives in the sample of size 100 is greater than or equal to (Q16)
Problem 12. (Continues previous problem.) In that case, the chance of rejecting the lot if it really has 50 defective chips is (Q17)
Problem 13. (Continues previous problem.) In the long run, the fraction of lots with 7 defectives that will get discarded erroneously by this test is (Q18)
Problem 14. (Continues previous problem.) The smallest number of defectives in the lot for which this test has at least a 98% chance of correctly detecting that the lot was bad is (Q19)
(Continues previous problem.) Suppose that whether or not a lot is good is random, that the long-run fraction of lots that are good is 95%, and that whether each lot is good is independent of whether any other lot or lots are good. Assume that the sample drawn from a lot is independent of whether the lot is good or bad. To simplify the problem even more, assume that good lots contain exactly 7 defective chips, and that bad lots contain exactly 50 defective chips.
Problem 15. (Continues previous problem.) The number of lots the manufacturer has to produce to get one good lot that is not rejected by the test has a (Q20) distribution, with parameters (Q21)
Problem 16. (Continues previous problem.) The expected number of lots the manufacturer must make to get one good lot that is not rejected by the test is (Q22)
Problem 17. (Continues previous problem.) With this test and this mix of good and bad lots, among the lots that pass the test, the long-run fraction of lots that are actually bad is (Q23)
Which graph shows the solution set for 2x+3 >-9?
o
8 -7 -6 -5 -4 -3 -2 -1 0
1 2
o
-6-5-4 - -21
0
1
2
0
-8 -7 -6 -5 -4 -3 -2 -1
0
1
2
O +
-8 -7 -6 -5 4 3 2-1
1
2
Save and Exit
Next
Submit
Mark this and return

Answers
I can't see pictures, but I'm going to solve the inequality and hope it helps.
2x+3>-9
-3 -3
2x>-12
/2 /2
x>-6
To graph this, you need to convert this to slope form.
x>-6/1
-6 is the rise, and 1 is the run. That means that when you start at the origin, (0,0), you go down 6 units, because of the negative, and go right 1 unit. Repeat until you have maybe about 3 points, or until you can make a line. Then because the inequality has >, you shade to the right.
---
hope it helps
sorry if it doesn't
There's another silence as Steve looks toward the crowd and then toward Tommy. He wears a tight grin.
STEVE
Based on the clues in this passage, what will most likely happen next?
• The neighbors will stop doubting Tommy.
Well, I guess what we'd better do then is to run a check on the neighborhood and see which ones of us are really human.
• The neighbors will stop taking Steve seriously.
• The neighbors will continue to joke about the situation.
There's laughter at this, but it's a laughter that comes
from a desperate attempt to lighten the atmosphere. It's a • The neighbors will begin checking to see who is release kind of laugh.
really human.
36. GROUP SHOT - THE PEOPLE 36.
As they look at one another in the middle of their laughter.
-The Monsters Are Due on Maple Street,
Rod Serling
Answers
Answer:
5
Step-by-step explanation:
A triangular prism has height 20 cm.
Its triangular face has base 7 cm and height 10 cm.
A. what is the volume of the prism?
B. suppose you triple the height of the prism.what happen to the volume?
C. suppose you triple the base of the triangular face.what happen to the volume?
D. suppose you triple the height of the triangular face.what happen to the volume?
E. suppose you triple all 3 dimensions.what happen to the volume?
Answers
Answer:
A. The volume of the triangular prism can be calculated using the formula V = (1/2)bh × h, where b is the base of the triangular face and h is the height of the prism. Thus, V = (1/2)(7 cm)(10 cm) × 20 cm = 700 cubic centimeters.
B. If the height of the prism is tripled to 60 cm, then the new volume would be V' = (1/2)(7 cm)(10 cm) × 60 cm = 2100 cubic centimeters. Thus, the volume is tripled.
C. If the base of the triangular face is tripled to 21 cm, then the new volume would be V' = (1/2)(21 cm)(10 cm) × 20 cm = 2100 cubic centimeters. Thus, the volume is tripled.
D. If the height of the triangular face is tripled to 30 cm, then the new volume would be V' = (1/2)(7 cm)(30 cm) × 20 cm = 2100 cubic centimeters. Thus, the volume is tripled.
E. If all three dimensions (base, height of triangular face, and height of prism) are tripled, then the new volume would be V' = (1/2)(21 cm)(30 cm) × 60 cm = 18900 cubic centimeters. Thus, the volume is multiplied by a factor of 27.
Find two consecutive whole numbers that 56 lies between.
(NEED ASAP PLEASE !!)
Answers
Find the measure of the largest angle in the triangle
shown.
15x
24x
21x
Answers
Answer:
72°
Step-by-step explanation:
Find the image of the question attached
The sum of angle in a triangle is 180°
Hence:
15x+24x+21x = 180°
60x =180
x =180/60
x= 3
Get the largest angle
The largest angle out of the angles is 24x
24x =24(3)
24(3) =72°
Hence the measure of the largest angle is 72°

Point Farmer Ed has 60 feet of fencing, and wants to enclose a rectangular plot that borders on a river. If Farmer Ed does not fence the side along the river, find the length and width of the plot that will maximize the area. What is the largest area that can be enclosed?
Answers
Answer:
Farmer Ed has 60 feet of fencing; and wants to enclose rectangular plot that borders on river: If Farmer Ed does not fence the side along the river; find the length and width of the plot that will maximize the area_ What is the largest area that can be enclosed? What width will maximize the area? The width, labeled x in the figure. (Type an integer or decimal ) What length will maximize the area? The length, labeled in the figure, is (Type an integer or decimal ) What is the largest area that can be enclosed? The largest area that can be enclosed is (Type an integer or decimal.)
You have 120 feet of fencing to enclose a rectangular plot that borders on a river.
In order to increase customer service, a muffler repair shop claims its mechanics can replace a muffler in 13 minutes. A time management specialist selected six repair jobs and found their mean time to be 12.3 minutes. The standard deviation of the sample was 2.3 minutes. At α=0.05, is there enough evidence to conclude that the mean time in changing a muffler is less than 13 minutes?
Answers
There is not enough evidence to conclude that the mean time in changing a muffler is less than 13 minutes.
To determine whether there is enough evidence to conclude that the mean time in changing a muffler is less than 13 minutes, we can conduct a one-sample t-test with the following hypotheses:
Null hypothesis: The true mean time in changing a muffler is equal to 13 minutes.
Alternative hypothesis: The true mean time in changing a muffler is less than 13 minutes.
Use the formula to calculate the test statistic,
\(t = \dfrac{(x - \mu)} { \dfrac{s} { \sqrt{n}}}\)
where x is the sample mean, μ is the hypothesized population mean (13 minutes), s is the sample standard deviation, and n is the sample size (6).
Plugging in the numbers, we get:
t = (12.3 - 13) / (2.3 / √6) = -0.72
Using a t-distribution table with 5 degrees of freedom (n - 1), we find that the critical value for a one-tailed test with α = 0.05 is -2.571. Since our calculated t-value (-0.72) is greater than the critical value, we fail to reject the null hypothesis.
Therefore, there is not enough evidence to conclude that the mean time in changing a muffler is less than 13 minutes.
To know more about the hypothesis follow
https://brainly.com/question/23730829
#SPJ1
someone please help me

Answers
9514 1404 393
Answer:
x = 6
Step-by-step explanation:
The ratio of the long segment to the whole is the same for both transversals.
(4x +3)/15 = (8+10)/10 = (whole)/(long segment)
2(4x +3) = 3(18) . . . . . . . multiply by 30
8x = 48 . . . . . . . . . . . . . . subtract 6, simplify
x = 6 . . . . . . . . divide by 8
A photograph is dilated to fit in a frame, so that its area after the dilation is 9 times greater than the area of the original
photograph. What is the scale factor of the dilation?
thank you!

Answers
Answer:
The answer is 3
Step-by-step explanation:
John wishes to choose a combination of two types of cereals for breakfast - Cereal A and Cereal B. A small box (one serving) of Cereal A costs $0.50 and contains 10 units of vitamins, 5 units of minerals, and 15 calories. A small box (one serving) of Cereal B costs $0.40 and contains 5 units of vitamins, 10 units of minerals, and 15 calories. John wants to buy enough boxes to have at least 500 units of vitamins, 600 units of minerals, and 1200 calories. How many boxes of each cereal should he buy to minimize his cost?
Answers
Let's assume that John buys x boxes of Cereal A and y boxes of Cereal B. Then, we can write the following system of inequalities based on the nutrient and calorie requirements:
10x + 5y ≥ 500 (minimum 500 units of vitamins)
5x + 10y ≥ 600 (minimum 600 units of minerals)
15x + 15y ≥ 1200 (minimum 1200 calories)
We want to minimize the cost, which is given by:
0.5x + 0.4y
This is a linear programming problem, which we can solve using a graphical method. First, we can rewrite the inequalities as equations:
10x + 5y = 500
5x + 10y = 600
15x + 15y = 1200
Then, we can plot these lines on a graph and shade the feasible region (i.e., the region that satisfies all three inequalities). The feasible region is the area below the lines and to the right of the y-axis.
Next, we can calculate the value of the cost function at each corner point of the feasible region:
Corner point A: (20, 40) -> Cost = 20
Corner point B: (40, 25) -> Cost = 25
Corner point C: (60, 0) -> Cost = 30
Therefore, the minimum cost is $20, which occurs when John buys 20 boxes of Cereal A and 40 boxes of Cereal B.
I need help please. aaaaaannnnnnnnndddddddddd thannkyou

Answers
Answer:
7:58
Step-by-step explanation:
The little hour hand is a bit past the 7. The long minute hand is closest to 12, which is 60 minuets. Just look the the mark that the little hand points at.
Which of these statements is true for f(x) = 2 · 3x?

Answers
Answer:
the statement number D okay!
The y-intercept of the function will be at (0, 2). Then the correct option is A.
What is an exponent?Let b is the base and x is the power of the exponent function and a is the leading coefficient. The exponent is given as
y = a(b)ˣ
The function is given below.
y = 2·(3)ˣ
The value of y at x = 0, we have
y = 2·3⁰
y = 2·1
y = 2
The y-intercept of the function will be at (0, 2).
Then the correct option is A.
More about the exponent link is given below.
https://brainly.com/question/5497425
#SPJ5

will mark brainliest please this is urgent

Answers
If a truck used 25 gallons to travel 375 mies, how many miles would it travel on 4 gallons of gas?
Answers
Answer:
93.75 miles if im not mistaken
Step-by-step explanation:
because the most miles is 375 so you would divide that number by four to see how many miles u can go before filling up again.
What is the perimeter of the parallelograrn?
Answers
A company’s sales increased 17% this year, to $8267. What were their sales last year?
Answers
Answer:
eekk im not shure sorry but it might be 8156 i no no
Step-by-step explanation:
Which expression is equivalent to: 7(y+3+2b)
Answers
Answer:
7y + 21 + 14b
Step-by-step explanation:
Use the distributive property.
7 x y = 7y
7 x 3 = 21
7 x 2b = 14b
7y + 21 + 14b
Without graphing, describe the transformations of each parabola or absolute value function 2) y =(x + 4) + 4 3) y=-2(x+4)² + 4 Fo 4 y = |x-31+3 5) y= 2(x - 1)2 + 4 T) y = -3/x-21 v- +11+3 = 2/x - 3/+4 9) y = 2|x1 + +1Please, solve for cases 3 and 4 only.

Answers
Solving for Case 3:
y = -2(x + 4)^2 + 4
We have that the parent function is:
y = x^2
This parabola has a transformation as follows:
1. It has a vertical shift of four units upward.
2. It moves four units to the left (a horizontal shift to left in four units.)
3. It is vertically stretched by 2 (its y-coordinates) and it is followed by a reflection across the x-axis (it was multiplied by -2.) In the latter, the parabola is open downward.
(In this case last case we have (x, y) ---> (x, -2y).)
Solving for the Case 4:
| x - 3 | + 3
In this case, the parent function is:
y = | x |
This function has a transformation as follows:
1. It has a horizontal shift to the right of three units.
2. It has a vertical shift upwards of three units.

I need help with this. -y^2+x^3-4x^3-6y^3+5-2x^3
Answers
Answer:
-y^2-5x^3-6y^3+5
Step-by-step explanation:
Collect the terms
ANSWER THIS CORRECTLY FOR BRAINLIEST (algebra)
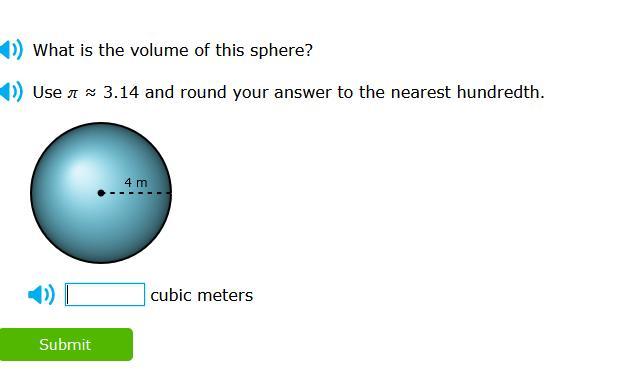
Answers
Answer:
267.95 cubic meters
Explanation:
volume of sphere: (4/3)π(radius)³
Here given:
radius: 4 meterVolume:
(4/3)π(radius)³insert values
(4/3)(3.14)(4)³simplify
(4/3)(3.14)(64)final answer
267.95 cm³Answer:
V = 267.95
Step-by-step explanation:
The equation to find the volume of a sphere is:
V = \(\frac{4}{3} \pi r^{3}\)
r = radius
In the diagram of the question it shows that the radius is 4 m. Plug this into the equation:
\(V=\frac{4}{3} (3.14) (4)^{3}\)
Use a calculator to find the answer and then round to two decimal points:
V = 267.95
Hope this helps!!
1) Matching.
The United States won 104 gold (g), silver s, and bronze (b) medals in the 2012 Summer Olympics.
____________a. Select the linear equation in standard form for three unknowns:
____________b. The United States won 46 gold medals and the same number each of silver and bronze medals. Select the relationship between the number of silver to bronze medals in an equation of two unknowns.
_____________c. With the information given in b, solve the linear equation in a for the number of gold, silver, and bronze medals won.
a. =g + s + b=104
b. =g=29, s=46, b=29
c. =g=b
d. =s=b
e =-g=46, s=29, b=29
f. =g + s + b=100

Answers
The linear equation in standard form is g + s + b=104, the relationship between silver to bronze medals is g = s and the solution is g=46, s=29, b=29
How to select the linear equation in standard form for three unknowns?
(a) Since the United States won 104 gold (g), silver s, and bronze (b) medals in the 2012 Summer Olympics.
This means the sum of gold (g), silver s, and bronze (b) medals is equal to 104. Thus, the linear equation in standard form is:
g + s + b = 104
(b) Since the United States won 46 gold medals and the same number each of silver and bronze medals. This implies:
g = 46
s = b
Thus, the relationship between the number of silver to bronze medals is s = b
(c) To solve the linear equation, substitute g = 46 and s = b into the equation g + s + b = 104:
g + s + b = 104
46 + b + b = 104
46 + 2b = 104
2b = 104 -46
2b = 58
b = 58/2
b = 29
Also, s = 29 (Remember: s = b)
Thus, g = 46, s =29, b = 29
Therefore, the United States won 46 gold (g), 29 silver (s), and 29 bronze (b) medals in the 2012 Summer Olympics. Select options a., d. and e. for a., b., and c. respectively
Learn more about linear equation on:
brainly.com/question/15602982
#SPJ1
Chris drove 265 miles using 10 gallons of gas. At this rate, how many gallons of gas would he need to drive 424 miles?
Answers
Answer:16
Step-by-step explanation:
265 / 10= 26.5 miles per gal.
424 miles / 26.5 mpg = 16 gallons
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
Answer: 0.6156 or in fraction form, 62%
Step-by-step explanation: To find the probability that at least one of the two people does not go on vacation, we subtract the probability that both of them go on vacation from 1. The probability that both go on vacation is 0.62 * 0.62 = 0.3844.
Therefore, the probability that one or both of them does not go on vacation is 0.6156, or about 62%.
Answer: 0.2356 and 0.1444
Step-by-step explanation:
62% of Americans go on Vacation
So out of 100 Americans, 62 go on vacation
The chance of one of them NOT going on vacation is 100-62 or 38%, however, the other person has to go on vacation, so it's 38%*62% or 0.2356, approx 40%*60% or 0.24
The chance of both of them do not go on vacation is 38%*38%, or 0.1444 or approx 40%*40% or 0.16 (very rough calculating)
Mrs. Jones bought 250 apples for $22 500. She sold 50 for $120 each, and the remain she sold 5 for $1 000 a parcel. (a) State whether she made a profit or loss. (b) Calculate her percentage profit or percentage loss.
Answers
Answer:
(a) yes
(b) 104% profit
Step-by-step explanation:
250 apples for $22,500 (were they gold?)
Part 1:
50x$120=$6000
Part 2:
200 sold at $1000 per 5 apples=200/5x1000=$40,000
$40,000+$6000=$46,000
A profit of $23,500
23500/22500=1.044 or 104% profit
A shoe boxmeasures 15 in.by 7 in. by 4 1/2 in what is the surface area of the box?
Answers
The surface area of the box is 408 in²
How to determine the surface area of the box?The surface area of the box can be calculated by using the formula for the surface of rectangular prism.
The surface area of rectangular prism is given by:
A = 2LW + 2WH + 2LH
Where L, W and H are the length, width and height of the prism respectively
L = 15 in, W = 7 in and H = 4 1/2 in
A = 2(15×7) + 2(7×4.5) + 2(15×4.5)
A = 210 + 63 + 135
A = 408 in²
Learn more about surface area of rectangular prism on:
brainly.com/question/26759265
#SPJ1
Please look at the photo. Thank you.

Answers
The output value of (f∘g)(x) is: \((f \circ g)(x) = \frac{4x^2-29x+60}{x +3}\)
The domain of (f∘g)(x) is (-∞, -3) U (-3, ∞).
How to determine the corresponding output value for this function?In this scenario, we would determine the corresponding composite function of f(x) and g(x) under the given mathematical operations (multiplication) in simplified form as follows;
\(f(x) = \frac{x-6}{x +3}\)
g(x) = 4x - 15
Next, we would write the numerators and denominators in factored form as follows;
(x - 6)(4x - 15)
4x² - 15x - 24x + 60
4x² - 29x + 60
Now, we can derive the corresponding composite function of f(x) and g(x);
\((f \circ g)(x) = \frac{4x^2-29x+60}{x +3}\)
For the restrictions on the domain, we would have to equate the denominator of the rational function to zero and then evaluate as follows;
x + 3 ≠ 0
x ≠ -3
Domain = (-∞, -3) U (-3, ∞).
Read more on domain here: brainly.com/question/17440903
#SPJ1