Ruth has 12 feet of ribbon.
She uses 7 feet of it for a craft project and gives 28 inches of it to her sister.
How many inches of ribbon does she have left?
Enter your answer in the box.
Answers
Answer:
See I don't know the answer but I did another one like this if it doesn't help you can report it no problem
Step-by-step explanation:
There are 2 different ways you can solve this problem and you'll get the same answer.
To help you visualize what you have to do, it might be easiest to translate your problem to a unit that easier to use.
Since you only have a ribbon 5 feet long, but you must cut it into 6 pieces, you know it won't even be 1 foot long.
One way to solve the problem would be to translate your 5-foot ribbon into a ribbon divided into inches.
1 foot = 12 inches
To find out how many inches long your ribbon is, you'll need to multiply the number of feet by 12.
Once you know that, then you can more easily divide it by 6. This will tell you how many inches each ribbon is.
Careful! the answer is to be put into feet so once you know how many inches long the ribbon is, you must then divide by 12 to get the correct answer in feet. Don't forget to round to the nearest tenth.
Another way to solve the problem is to simply divide the 5 feet by the number 6 and then round your number to the nearest tenth. It may be harder to visualize the answer this way, but you will get the same answer as if you translated your ribbon into inches and then divided by 12.
Good luck! I hope this helps!

Related Questions
What is the value of the digit in the ones place?
2,615
A. 50
B. 5
OC. 2,000
OD. 100
Answers
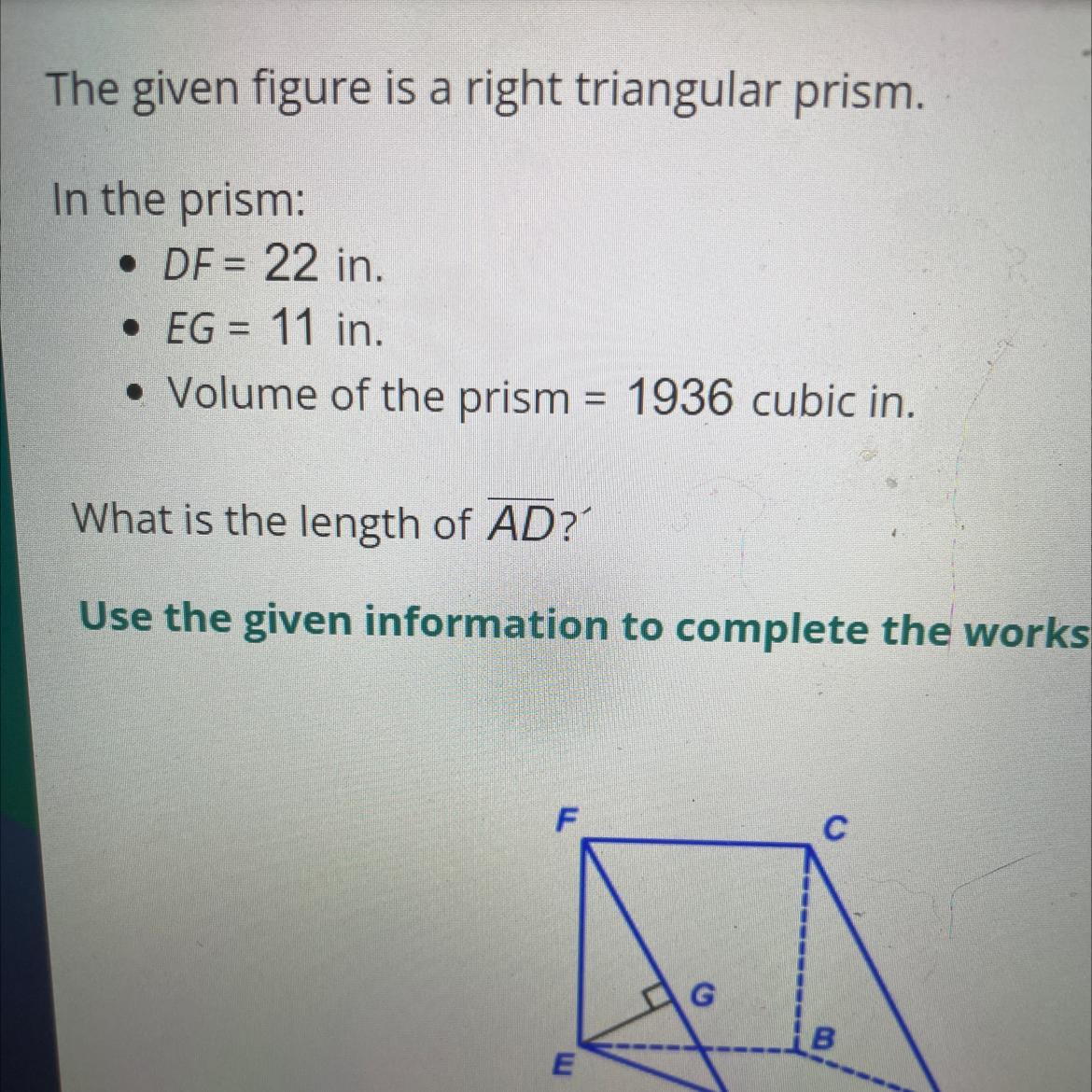
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Find theValue of x
40°
70°
(5x+10)°

Answers
Value of an exterior angle of a triangle is equal to the sum of values of two opposite interior angles of a triangle.
therefore,\(\qquad\displaystyle \tt \dashrightarrow \: 5x + 10 = 40 + 70\)
\(\qquad\displaystyle \tt \dashrightarrow \: 5x = 110 - 10\)
\(\qquad\displaystyle \tt \dashrightarrow \: 5x = 100\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 100 \div 5\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 20\)
Value of x = 20°
Hey! there . Thanks for your question :)
Answer:
20° is the correct answer.Step-by-step explanation:
In this question we are given with two interior angles of the triangle that are 40° and 70° , also we are given an exterior angle that is (5x + 10)°. And we are asked to find the value of angle x.
Solution :-
For finding the value of angle x , we have to use exterior angle property of triangle which states that sum of opposite interior angles of triangle is equal to the given exterior angle. So :
Step 1: Making equation :
\( \longmapsto \: \sf{40 {}^{°} + 70 {}^{°} = (5x + 10) {}^{°} }\)
Solving :
\( \longmapsto \: \sf{110 {}{°} = (5x) {}^{°} +10 {}^{°} }\)
Step 2: Subtracting 10 on both sides :
\( \longmapsto \sf{ 110 {}^{°} - 10 {}^{°} = 5x + \cancel{10 {}^{°}} - \cancel{10 {}^{°} } }\)
We get ,
\( \longmapsto \sf{(5x ){}^{°} = 100 {}^{°} }\)
Step 3: Dividing both sides by 5 :
\( \longmapsto \dfrac{ \cancel{5}x {}^{°} }{ \cancel{5}} = \dfrac{ \: \: \: \: \cancel{ 100} {°}^{} }{ \cancel{5} }\)
On cancelling , we get :
\( \longmapsto \underline{\boxed{\red{\sf{ \bold{ x = 20 {}^{°} }}}}} \: \: \bigstar\)
Therefore , value of x is '20°'Verification :-
For verifying sum of both the interior angles is equal to given exterior angles. As we get the value of x as 20 we need to substitute it's value in place x and then L.H.S must be equal to R.H.S :
40° + 70° = 5(20°) + 10°110° = 100° + 10°110° = 110°L.H.S = R.H.STherefore , our answer is correct .
Hope , it'll help you! :)#\( \underline{ \sf{ \bold{ Keep \: Learning }}}\)?
58 62
28 27 13
13 15 12 11
6 7 8 4 7
4 2 5 3 1 6
Answers
Answer:
105
Step-by-step explanation:
First, adding two sequence numbers and that result become upper number
Solve the following:
a) 2(5x - 3) = 24
Answers
Answer:
x=3
Step-by-step explanation:
\(2(5x - 3) = 24\\\\10x-6=24\\\\10x=24+6\\\\10x=30\\\\x=30/10\\\\x=3\)
Answer:
open the bracket by multiplying everything in the bracket by2
then you get
2×5x-2×-3=24
10x-6=24
10x=24+6
10x=30
x=3
Graph the linear equation.
x - 2y = - 2

Answers
The graph of the linear equation can be seen in the image below.
How to graph the linear equation?Here we have the linear equation:
x - 2y = -2
To graph it, we need to find two points that belong to the line, and then we can graph these and connect them with a line.
If x = 0, we have:
0 - 2y = -2
y = -2/-2 = 1
if x = 1 then:
1 - 2y = -2
1 + 2 = 2y
3 = 2y
3/2 = y
Then we have the points (0, 1) and (1, 3/2), now just graph these points on a coordinate axis and then connect them with a line, we will get:
If you want to learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1

A = multiples of 5 between 14 and 26
B = odd numbers between 14 and 26
(a) List the members of (A ∪ B)
Answers
Answer:
(A ∪ B) = {15, 17, 19, 20, 21, 23, 25}
Step-by-step explanation:
Multiples of 5:
{0, 5, 10, 15, 20, 25, ...}
So between 14 and 26:
A = {15, 20, 25}
Odd numbers between 14 and 26:
B = {15, 17, 19, 21, 23, 25}
(A ∪ B)
All numbers that are part of at least one of these sets. So
(A ∪ B) = {15, 17, 19, 20, 21, 23, 25}
Dana is making bean soup. The recipe she has makes 10 servings and uses
3/4
of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup?
She has
1/16
of a pound of beans in one container and
1/4
of a pound of beans in another container. How many more pounds of beans does Dana need to make the 5 servings of soup? Show your work or explain your answer.
Answers
A variable is normally distributed with mean 6 and standard 2 deviation .
a. Find the percentage of all possible values of the variable that lie between 5 and 9.
b. Find the percentage of all possible values of the variable that exceed 1.
c. Find the percentage of all possible values of the variable that are less than 4.
Answers
The normal distribution is also known as the Gaussian distribution. The percentage of all possible values of the variable that are less than 4 is 15.87%.
What is a normal distribution?
The normal distribution, also known as the Gaussian distribution, is a symmetric probability distribution about the mean, indicating that data near the mean occur more frequently than data distant from the mean. The normal distribution will show as a bell curve on a graph.
A.) The percentage of all possible values of the variable that lie between 5 and 9.
P(5<X<9) = P(X<9) - P(5<X)
= P(z<1.5) - P(-0.5<z)
= 0.9332 - 0.3085
= 0.6247
= 62.47%
B.) The percentage of all possible values of the variable that exceed 1.
P(X>1) = 1 - P(X<-2.5)
= 1-0.0062
= 0.9938
= 99.38%
C.) The percentage of all possible values of the variable that are less than 4.
P(X<4) = P(X <4)
= P(z<-1)
= 0.1587
= 15.87%
Learn more about Normal Distribution:
https://brainly.com/question/15103234
#SPJ1
graph h(x)=(x-1)^2-9
Answers
The graph of h(x) = (x-1)^2 - 9 is a U-shaped parabola that opens upwards, with the vertex at (1, -9), and it extends indefinitely in both directions.
The function h(x) = (x-1)^2 - 9 represents a quadratic equation. Let's analyze the different components of the equation to understand the behavior of the graph.
The term (x-1)^2 represents a quadratic term. It indicates that the graph will have a parabolic shape. The coefficient in front of the quadratic term (1) implies that the parabola opens upwards.
The constant term -9 shifts the graph downward by 9 units. This means the vertex of the parabola will be at the point (1, -9).
Based on this information, we can draw the following conclusions:
The graph will be a U-shaped curve with the vertex at (1, -9).
The vertex represents the minimum point of the parabola since it opens upward.
The parabola will be symmetric with respect to the vertical line x = 1 since the coefficient of the quadratic term is positive.
The graph will extend indefinitely in both directions.
To accurately plot the graph, you can choose several x-values, substitute them into the equation to find the corresponding y-values, and then plot the points on the graph. Alternatively, you can use graphing software or calculators that can plot the graph of the equation for you.
Remember to label the axes and indicate the vertex at (1, -9) to provide a complete representation of the graph of h(x) = (x-1)^2 - 9.
for such more question on parabola
https://brainly.com/question/9201543
#SPJ8
What two numbers multiply to -35 and add to get -18
Answers
he two numbers that multiply to -35 and add to get -18 are -5 and 3.
To see why, you can use the factoring method. First, find two numbers that multiply to give you -35. The factors of -35 are -1, 1, -5, and 5. So, the two numbers that multiply to -35 are either -5 and 7 or 5 and -7.
Next, find which pair of numbers adds up to -18. It's clear that 5 and -7 add up to -2, so they don't work. However, if we choose -5 and 3, we get:
-5 + 3 = -2
So, -5 and 3 are the two numbers that multiply to -35 and add to -18.
100 Points! Algebra question. Photo attached. Use a trigonometric function to find the value of x. Round to the nearest tenth if necessary. Please show as much work as possible. Thank you!

Answers
The value of x for each item is given as follows:
a) x = 3.9.
b) x = 32.6º.
What are the trigonometric ratios?The three trigonometric ratios are the sine, the cosine and the tangent, and they are obtained according to the rules presented as follows:
Sine of angle = opposite side/hypotenuse.Cosine of angle = adjacent side/hypotenuse.Tangent of angle = opposite side/adjacent side = sine/cosine.For item a, we have that x is opposite to the angle of 63º, while 2 is the adjacent side, hence:
tan(63º) = x/2
x = 2 x tangent of 63 degrees
x = 3.9.
For item b, we have that x is the angle, while 7 is the opposite side and 13 is the hypotenuse, hence:
sin(x) = 7/13
x = arcsin(7/13)
x = 32.6º.
Learn more about trigonometric ratios at brainly.com/question/24349828
#SPJ1
Instructions: Identify the type of sequence and write the explicit rule. write Explicit Rule Sequence: -39, -45, 51, 57,... Type: Arithmetic e Explicit Rule:
Answers
The given sequence does not follow a simple arithmetic or geometric pattern, making it challenging to determine an explicit rule based on the given terms.
To identify the type of sequence and write the explicit rule, we need to examine the pattern of the given sequence: -39, -45, 51, 57, ...
By observing the differences between consecutive terms, we can determine if it follows an arithmetic or geometric pattern.
Arithmetic sequences have a common difference between each term, meaning that by adding (or subtracting) the same value repeatedly, we can generate the sequence. Geometric sequences, on the other hand, have a common ratio between each term, meaning that by multiplying (or dividing) by the same value repeatedly, we can generate the sequence.
Let's calculate the differences between consecutive terms:
-45 - (-39) = -6
51 - (-45) = 96
57 - 51 = 6
From the differences, we can see that the sequence is not arithmetic since the differences are not constant. However, the differences alternate between -6 and 6, indicating a possible geometric pattern.
Let's calculate the ratios between consecutive terms:
-45 / (-39) ≈ 1.1538
51 / (-45) ≈ -1.1333
57 / 51 ≈ 1.1176
The ratios are not constant, indicating that the sequence is neither geometric nor arithmetic.
Therefore, the given sequence does not follow a simple arithmetic or geometric pattern, and it is difficult to determine the explicit rule based on the given terms. It is possible that the sequence follows a more complex pattern or rule that is not apparent from the given terms.
For more such question on arithmetic. visit :
https://brainly.com/question/7882626
#SPJ8
Complete the square to re-write the quadratic function in vertex form:
y= x2 - 5x +9
Answer: y =
Submit Answer
Answers

A loan of $7,000 for 4 acres of woodland is compounded somiannually at an annual rate of 8% for 3 years.
How much INTEREST is paid at the end of 3 years?
Answers
Answer:
$560
Step-by-step explanation:
A rectangular parking lot has a length that is 9 yards greater than the width. The area of the parking lot is 360 square yards. Find the length and the width.
Answers
Answer: The width is 15 yards and the length is 24 yards
Step-by-step explanation:
Let x represent the width of the parking lot in yards
Let the length of the parking lost be (x + 9) as the length is 9 yards greater than the width
So, area = width * length
i.e. 360 = x(x + 9)
360 = x2 + 9x
x2 + 9x - 360 = 0
x2 + 24x - 15x - 360 = 0
x(x + 24) - 15(x + 24) = 0
(x + 24)(x - 15) = 0
Either x = -24 or, x = 15
But as width can not be negative, so we can not have, x = -24
So, we have, x = 15
Therefore, (x + 9) = (15 + 9) = 24
So, we have the following answers.
Width : 15 yards
Length : 24 yards
Ultrasound waves are used in Indoor Positioning Systems in hospitals to detect the location of equipment. If the system must be centrally located in a hospital that measures 860 meters in the east-west direction by 950 meters in the north-west direction, which would be an equation that models the range of the IPS for this hospital?
Answers
The equation that models the range of the Indoor Positioning System (IPS) in this hospital is Range^2 = 410,525.
To model the range of the Indoor Positioning System (IPS) in a hospital that measures 860 meters in the east-west direction by 950 meters in the north-west direction, we can consider the range as a function of the distance from the central location. Let's assume the central location is the origin (0,0) on a Cartesian coordinate system.
The range of the IPS can be modeled using the Pythagorean theorem, as it measures the distance between two points in a Cartesian plane. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
In this case, the range of the IPS can be represented by the equation:
Range^2 = x^2 + y^2
Where x represents the distance in the east-west direction and y represents the distance in the north-west direction from the central location.
Given the dimensions of the hospital (860 meters in the east-west direction and 950 meters in the north-west direction), we can substitute the values into the equation to get:
Range^2 = (860/2)^2 + (950/2)^2
Simplifying this equation, we have:
Range^2 = 430^2 + 475^2
Therefore, the equation that models the range of the IPS for this hospital is:
Range^2 = 184,900 + 225,625
To learn more about Cartesian coordinate system
https://brainly.com/question/4726772
#SPJ8
3) Which graph represents a function?
X
2
10

Answers
Answer:
D (Bottom right choice)
Step-by-step explanation:
This is because we have a linear line that changes the same amount every time.
The bottom right graph
Explanation:
Because the graph is going in a straight line. And the rate of change is constant
select an expression that is equivalent to 2^4/8

Answers
Answer:
The answer is C
Step-by-step explanation:

c. 8√(2^4 )
given 2^(4/8) can be written as 2^(4×1/8)
eg: 2^(1/2) is √2 hence same rule we can apply here and since 2^(1/8) we can write as 8√2 and given 2^4
further knowledge: so if asked to expand more we can write it as 8√16 simplifying this further we get 2^(1/2) which is actually √2
for more on square roots: https://brainly.com/question/29286039
how do i do this ive been struggling for 45 minutes and i can’t seem to solve it…

Answers
The quadratic function for the value of David's investment indicates;
(i) $45,000
(ii) 9.375 months
What is a quadratic function?A quadratic function is a function that can be expressed in the form; f(x) = a·x² + b·x + c, where a ≠ 0, and a, b, and c are numbers.
The model of the value of the investment in the bank obtained from the amount of his retirement funds David invested in the bank can be presented as follows;
a = 45 + 75·t - 4·t²
Where;
a = The value of the investment in thousand of dollars after t months
t = The number of months of the investment
(i) The initial amount David invested can be found by plugging in t = 0, in the function for the amount David invested in the bank, as follows;
a = 45 + 75 × 0 - 4 × 0² = 45
The initial amount David invested is; a = $45,000
(ii) The number of months it takes for David investment to reach a maximum value can be found from the quadratic function as follows;
The number of months t(max) at the maximum amount is; t(max) = -75/(2 × (-4)) = 9.375
Therefore, it will take 9.375 months for David's investment to reach a maximum value
Learn more on the maximum value of a quadratic function here: https://brainly.com/question/11170631
#SPJ1
Choose the correct answer
The triangle below is rotated about the x- axis
(Choices are in the picture)

Answers
Answer:
see attached
Step-by-step explanation:


) Assume that a simple random sample has been selected from a normally distributed population and test the given claim at α = 0.05. State the claim mathematically. Identify the null and alternative hypotheses, test statistic, critical region(s), and the decision regarding the null hypothesis. State the conclusion that addresses the original claim. A local group claims that police issue at least 60 speeding tickets a day in their area. To prove their point, they randomly select two weeks. Their research yields the number of tickets issued for each day. The data are listed below. 70 48 41 68 69 55 70 57 60 83 32 60 72 58
Answers
We cannot conclude that there are more than 70,000 defined words in the dictionary.
To test the claim that there are more than 70,000 defined words in the dictionary, we can set up the null and alternative hypotheses as follows:
Null Hypothesis (H0): The mean number of defined words on a page is 48.0 or less.
Alternative Hypothesis (H1): The mean number of defined words on a page is greater than 48.0.
So, sample mean
= (59 + 37 + 56 + 67 + 43 + 49 + 46 + 37 + 41 + 85) / 10
= 510 / 10
= 51.0
and, the sample standard deviation (s)
= √[((59 - 51)² + (37 - 51)² + ... + (85 - 51)²) / (10 - 1)]
≈ 16.23
Next, we calculate the test statistic using the formula:
test statistic = (x - μ) / (s / √n)
In this case, μ = 48.0, s ≈ 16.23, and n = 10.
test statistic = (51.0 - 48.0) / (16.23 / √10) ≈ 1.34
With a significance level of 0.05 and 9 degrees of freedom (n - 1 = 10 - 1 = 9), the critical value is 1.833.
Since the test statistic (1.34) is not greater than the critical value (1.833), we do not have enough evidence to reject the null hypothesis.
Therefore, based on the given data, we cannot conclude that there are more than 70,000 defined words in the dictionary.
Learn more about test statistic here:
https://brainly.com/question/31746962
#SPJ1
Watch help video
The point A is plotted on the coordinate grid below. Plot the point A', the reflection
of A over the x-axis.
Click on the graph to plot a point. Click a point to delete it.
5
3
N
A
T
3
2
1
2
A
3
5
Answers
Answer:
The answer is point A' (3, -2).
3
\(3 \sqrt{81} \)
what's the answer
Answers
Answer will be 27.
Given,
3√81
Now, to solve the expression the squares of whole numbers and square roots for some numbers must be known.
For example, squares of
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
Square roots,
√100 = 10
√81 = 9
√64 = 8
√49 = 7
√36 = 6
√25 = 5
√16 = 4
√9 = 3
√4 = 2
√1 = 1
Now ,
3√81 = 3× 9
= 27.
Thus the value is 27.
Know more about Square roots,
https://brainly.com/question/16113248
#SPJ1
No rush but please help

Answers
Answer:
C. .
Irrational numbers are those, which are non-recurring and non-terminating.
I hope it will be useful.
Answer:
C
Step-by-step explanation:
The diet of a jellyfish consists primarily of plankton, which are tiny
organisms living in the ocean. One species of plankton has an average length
of 0.08 inches. Suppose a certain jellyfish has a length of 12 cinches. Write
a percent that compares the length of the plankton to the length of the
jellyfish.

Answers
Answer:
To compare the length of the plankton to the length of the jellyfish, we can express the length of the plankton as a percentage of the length of the jellyfish.
First, we need to convert the length of the jellyfish from inches to centimeters so that we can compare the two measurements in the same unit.
12 inches = 12*2.54 = 30.48 cm
Next, we divide the length of the plankton by the length of the jellyfish and multiply by 100 to get the percentage.
0.08 inches / 30.48 cm * 100 = 0.00262 * 100 = 0.262%
So, the length of the plankton is 0.262% of the length of the jellyfish.
Brainliest if correct
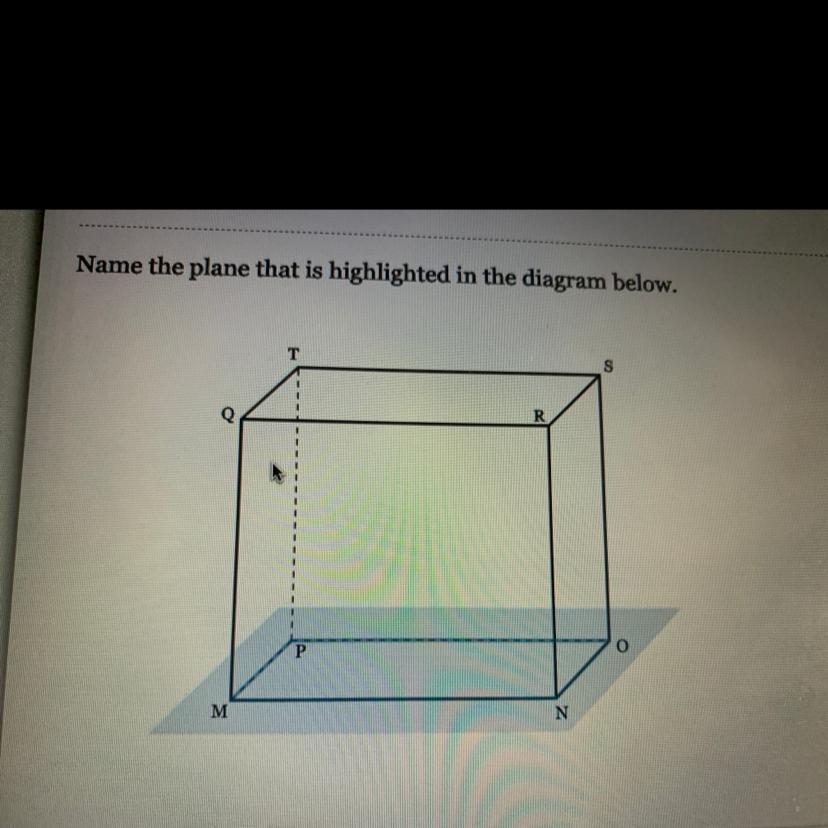
Answers
Answer:
The plane is:
MPON (or MNOP)This is containing the bottom face of the prism
Answer:
cuboid is shown in figure having
the plane is MNOP
I NEED ANSWER ASAP PLEASE WITH WORK PLEASE AND TY!!!!!! In the image the question is 32!! What is the factored form of x2 + 12x - 64?
A (x-4)(x + 16)
B. (x-2)(x + 32)
C. (x + 4)(x - 16)
D. (x-6)(x + 18)

Answers
Answer:
A) (x-4)(x+16)
Step-by-step explanation:
\(x^2+12x-64\\=x^2-4x+16x-64\\=x(x-4)+16(x-4)\\=(x+16)(x-4)\)
Hi I need help.
An education reform lobby is compiling data on the state of education in the United States. In their research they looked at the percent of people who graduate high school in 10 different states. The data are provided below. Use a TI-83, TI-83 Plus, or TI-84 to calculate the sample standard deviation and the sample variance.
Round your answers to one decimal place.
High School Graduation Rate (%)
77.1
82.9
90
91.3
81.9
83.3
84.9
82.5
84.6
Answers
The sample variance and standard deviation are given as follows:
Variance = 87.22 %.
Standard deviation = 9.34%.
To obtain the variance and the standard deviation first, we must obtain the mean, which is given by the sum of all observations divided by the number of observations, hence:
Mean = (77.1 + 82.9 + 90 + 91.3 + 81.9 + 83.3 + 84.9 + 82.5 + 84.6)/10
Mean = 75.85.
Then we must obtain the sum of the differences squared between each observation and the mean, as follows:
(77.1 - 75.85)² + (82.9 - 75.85)² + (90 - 75.85)² + (91.3 - 75.85)² + (81.9 - 75.85)² + (83.3 - 75.85)² + (84.9 - 75.85)² + (82.5 - 75.85)² + (84.6 - 75.85)² = 784.9825
The sample variance is given by the above sum divided by one less than the sample size, hence:
Variance = 784.9825/9
Variance = 87.22 %.
The standard deviation is the square root of the variance, hence:
Standard deviation = sqrt(87.22)
Standard deviation = 9.34%.
To learn more about standard deviation here:
brainly.com/question/30240469
#SPJ4
I need help ASAP please giving brainliest

Answers
Answer:
Step-by-step explanation:
A and B form a right angle
meaning that A+B=90
if A=58
B=90-58 = 32
answers
B is acute angle, true
second statement is False
Last statement is true