Richard and Teo have a combined age of 21. Richard is 3 years older than twice Teo’s age. How old are Richard and Teo?
Answers
Answer:
Richard's age = 15
Teo's age = 6
Step-by-step explanation:
Let's say Teo's age is x.
Then, we will get this very equation.
\(3 + 2x \)
The equation above is Richard's age.
\(x + 2x + 3 = 21\)
This equation is their ages conbined.
Now, let's solve the equation.
Collect like terms.
\(3x + 3 = 21\)
Move the constant. ( Which is 3, in this case. )
\(3x = 21 - 3\)
Calculate.
\(3x = 18\)
Because we want only "x", divide both sides of the equation by 3.
\(x = 6\)
As I have said above, "x" is Teo's age.
Let's find Richard's.
It is:
2x + 3
x is 6.
(2 x 6) + 3
12 + 3
15 ( Richard's age.)
I hope it helps.
Answer:
Two's age = 6 years.Richard's age = 15 yearsStep-by-step explanation:
In the question ,
Given :
Richard and Two have combined age of 21. Richard is 3 years older than twice Two's ageAnd , we have to find the ages of Richard and Teo . So we are assuming that Teo's age be x . Therefore Richard's age be 2x + 3 ( because in the question it is given that Richard is 3 years older than twice the age of Teo ) .
According to question , we are adding Richard's age and Teo's age :
\(\longrightarrow \: x + 2x + 3 = 21\)
Step 1 : Adding the like term in left hand side :
\(\longrightarrow \: 3x + 3 = 21\)
Step 2 : Transposing 3 to right hand side :
\(\longrightarrow \: 3x = 21 - 3\)
Step 3 : By Subtracting 3 from 21 , We get :
\(\longrightarrow \: 3x = 18\)
Step 4 : Transposing 3 to right hand side :
\(\longrightarrow \: x = \cancel\frac{18}{3} \)
Step 5 : Now dividing 18 by 3 :
\(\longrightarrow \: \red{\boxed{ x = 6}}\)
We know that ,
x = Teo's age 6Therefore , Teo's age is 6 year old .And ,2x + 3 = Richard's age2 ( 6 ) + 312 + 315Therefore , Richard's is 15 year old#Keep LearningRelated Questions
two times a number less 4 is greater than the same number plus 6. for what number or numbers is true?
Answers
Answer:
n > 10 meaning, n is greater than 10
Step-by-step explanation:
Two times a number : 2n
Less 4 : -4
2n-4
Greater than the same number : >n
Plus 6 : +6
> n+6
2n-4 > n+6
To find n, we have to get n alone and equal to a single number. To do this, we first subtract 6 from both sides.
2n-10 > n
Then, subtract 2n from both sides
-10 > -n
Now, divide by -1
10 < n
So, n is greater than 10
the dimensions of the rectangular pool shown below are 40 yards by 20 yards. A fence will be built around the outside of the deck. The ratio of the dimensions of the fence to the dimensions of the pool is 3/2. How many yards of fence should be purchased?
Answers
90 yards of fence should be purchased
How many yards of fence should be purchased?We have:
Dimensions of the pool: 40 yards by 20 yards
Ratio of the dimensions of the fence to the dimensions of the pool: 3/2
Thus, we can say:
The length of the fence is:
3/2 * 40 yards = 60 yards
The width of the fence is:
3/2 * 20 yards = 30 yards
The total length of the fence is:
60 yards + 30 yards = 90 yards
Therefore, 90 yards of fence should be purchased
Learn more about dimension on:
https://brainly.com/question/27404871
#SPJ1
A package of 3 pairs of insulated gloves costs $25.77. What is the unit price of the pairs of gloves? The unit prices is $ per pair of gloves
Answers
pls help me with this question and pls don't answer if you don't know. thank you,
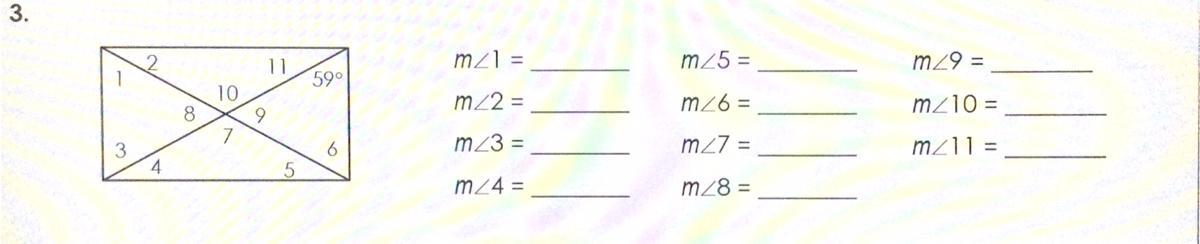
Answers
Answer:
I apologize if this was poorly explained. The explanation for each is below the angle.
Since these triangles are in a rectangle, The top and bottom triangles are congruent, and the left and right triangles are congruent. All 4 triangles are also Isosceles. (Two equal sides/angles)
m<1= 59
(Left and right triangles are congruent)
m<2=31
(Top and bottom triangles are congruent)
m<3= 59
(Directly across from the other 59)
m<4=31
(Each of the rectangles corner angles totals to 90 degrees, therefore making this angle 31 degrees.)
m<5=31
(Since the triangles are isosceles, this angle is also 31)
m<6= 59
(Since m<5 is 31, this angle is 59.)
m<7=118
{(Two other angles in the triangle) 31+31= 62 180-62= 118)}
m<8=62
{(Two other angles in the triangle)59+59= 118. 180-118= 62}
m<9=62
(This angle and m<8 are congruent.)
m<10=118
(This angle and m<7 are congruent.)
m<11=31
(Same reason as m<4)
I hope this helps!
Simplify: (4 /5 + 6/ 25 ) X (8/ 9 + −8 /7 )
Answers
Answer: -416/1575
Step-by-step explanation:
\(\frac{4}{5}=\frac{20}{25} \implies \frac{4}{5}+\frac{6}{25}=\frac{26}{25}\\\)
\(\frac{8}{9}=\frac{56}{63}\\\\-\frac{8}{7}=-\frac{72}{63}\\\\\implies \frac{8}{9}-\frac{8}{7}=-\frac{16}{63}\)
\(\frac{26}{25} \times -\frac{16}{63}=-\frac{416}{1575}\)
Please help me solve this. With Reasoning
6 2/5 - 4 2/3
Answers
Answer:
1 and 11/15.
Step-by-step explanation:
To solve, we can separate the integers from the fractions.
(6 - 4) + (2/5 - 2/3)
= 2 + (6/15 - 10/15)
= 2 + (-4/15)
= 1 + 15/15 - 4/15
= 1 + 11/15
= 1 and 11/15
Hope this helps!
Maria has made $28 selling bracelets at a craft fair. She spends $52 on supplies to make the bracelets. She sells each bracelet for $3. Which inequality can Maria use to find how many more bracelets she needs to sell to make more money than she spent on supplies. A. 3x + 52 < 28 B. 28x +3 >52 C. 3x + 28 < 52 D. 3x +28 > 52
Answers
Answer: D. 3x +28 > 52
Step-by-step explanation:
Based on the information given, the inequality that Maria can use to find how many more bracelets she needs to sell to make more money than she spent on supplies will be calculated thus:
With the question above, the total sales must be greater than the amount spent on supplies. Let the number of bracelets that needs to be sold be represented by x.
Therefore, (3 × x) + 28 > 52
= 3x + 28 > 52.
We can calculate further
3x > 52 - 28
3x > 24
x > 24/3
x > 8
Therefore, 9 or more bracelets needs to be sold since x is greater than 8.
Therefore, the correct option is D 3x +28 > 52
Answer:
D. 3x + 28 > 52
Step-by-step explanation:
use tukey’s procedure on the data in example 10.3 to identify differences in true average bond strengths among the five protocols
Answers
Tukey's procedure, also known as the Tukey-Kramer test, a statistical method used to compare multiple groups and identify significant differences in their means. Tukey's procedure is used to identify differences in the true average bond strengths among the five protocols in Example 10.3.
Tukey's procedure, also known as the Tukey-Kramer test, a statistical method used to compare multiple groups and identify significant differences in their means. In this case, we are applying Tukey's procedure to the data in Example 10.3, which consists of bond strengths measured under five different protocols.
To perform Tukey's procedure, we first calculate the mean bond strength for each protocol. Next, we compute the standard error of the mean for each protocol. Then, we calculate the Tukey's test statistic for pairwise comparisons between the protocols. The test statistic takes into account the means, standard errors, and sample sizes of the groups.
By comparing the Tukey's test statistic to the critical value from the studentized range distribution, we can determine if there are statistically significant differences in the true average bond strengths among the protocols. If the test statistic exceeds the critical value, it indicates that there is a significant difference between the means of the compared protocols.
Using Tukey's procedure on the data in Example 10.3 will allow us to identify which pairs of protocols have significantly different average bond strengths and provide insights into the relative performance of the protocols in terms of bond strength.
Learn more about test statistic here:
https://brainly.com/question/31746962
#SPJ11
One number is 4 less than 3 times a second number. If 3 more than two times the first
number is decreased by 2 times the second number, the result is 11. Use the substitution
method. What is the first number?
Answers
Answer:
The first number (x) = 8
Step-by-step explanation:
Let x = the first number
Let y = the second number
x = 3*y - 4
2x + 3 - 2y = 11 Subtract 3 from both sides
2x - 2y = 11 - 3
2x - 2y = 8 Divide by 2
x - y = 4 Add y to both sides
x = y + 4 Now go back to the very first equation. Substitute for x
y + 4 = 3y - 4 Subtract y from both sides
4 = 3y - y - 4
4 = 2y - 4 Add 4 to both sides
4 + 4 = 2y
8 = 2y Divide by 2
8/2 = y
y = 4
x = 3y - 4
x = 3*4 - 4
x = 12 - 4
x = 8
Solve the following recurrence relations. a) T(n)=T(n−1)+3,T(1)=0 b) T(n)=3T(n−1) for n>1,T(1)=2. c) T(n)=T(n/2)+2n for n>1,T(1)=1, you may assume n=2 k
Answers
(a) To solve the recurrence relation T(n) = T(n-1) + 3, we can expand it recursively:
T(n) = T(n-1) + 3
= (T(n-2) + 3) + 3
= T(n-2) + 2*3
= T(n-3) + 3*3
= T(n-4) + 4*3
= ...
= T(n-k) + k*3
We can observe that T(n-k) = T(1) = 0, as given in the initial condition. So, we have:
T(n) = T(n-k) + k*3
= 0 + k*3
= 3k
Therefore, the solution to the recurrence relation T(n) = T(n-1) + 3 with T(1) = 0 is T(n) = 3n.
(b) To solve the recurrence relation T(n) = 3T(n-1) with T(1) = 2, we can expand it recursively:
T(n) = 3T(n-1)
= 3*(3T(n-2))
= 3*(3*(3T(n-3)))
= ...
= 3^k * T(n-k)
We can observe that T(n-k) = T(1) = 2, as given in the initial condition. So, we have:
T(n) = 3^k * T(n-k)
= 3^k * 2
Since n = n - k, we can solve for k:
n - k = 1 => k = n - 1
Substituting this value of k into the solution, we get:
T(n) = 3^(n-1) * 2
Therefore, the solution to the recurrence relation T(n) = 3T(n-1) with T(1) = 2 is T(n) = 3^(n-1) * 2.
(c) To solve the recurrence relation T(n) = T(n/2) + 2n with T(1) = 1, we can expand it recursively:
T(n) = T(n/2) + 2n
= (T(n/4) + 2*(n/2)) + 2n
= T(n/4) + 2*(n/2) + 2n
= T(n/4) + 3n
= (T(n/8) + 2*(n/4)) + 3n
= T(n/8) + 2*(n/4) + 3n
= T(n/8) + 4n/2 + 3n
= T(n/8) + 7n/2
= ...
= T(n/2^k) + (2^k - 1)n/2
We can observe that T(n/2^k) = T(1) = 1, as given in the initial condition. So, we have:
T(n) = T(n/2^k) + (2^k - 1)n/2
= 1 + (2^k - 1)n/2
Since n = 2^k, we can solve for k:
2^k = n => k = log2(n)
Substituting this value of k into the solution, we get:
T(n) = 1 + (2^(log2(n)) - 1)n
To learn more about recurrence relation:https://brainly.com/question/4082048
#SPJ11
Which of the following algebraic represents shows a dilation that is an enlargement ?
Answers
The algebraic representation that shows a dilation that is an enlargement is (5/2 x,5/2 y). (Option D)
A dilation is a type of transformation that changes the size of the shape or object. It refers to a process of changing an object’s size by decreasing or increasing its dimensions by a scaling factor. A dilation produces an image that has the same shape as the original image but is a different size.
A dilation that results in a larger image is called an enlargement while a dilation that generates a smaller image is called a reduction. A dilation is described using the scale factor and the center of the dilation (which is a fixed point in the plane).
For a scale factor > 1, the image is an enlargement; for a scale factor < 1 and > 0, the image is a reduction; and for a scale factor = 1, the figure and the image are congruent. Hence, for a point (x,y), algebraic representation that shows a dilation that is an enlargement is (5/2 x,5/2 y) as the scale factor is greater than 1. For the remaining options, the scale factor is between 0 and 1, hence they are reduction.
Note: The question is incomplete. The complete question probably is: Which of the following algebraic representation shows a dilation that is an enlargement? A) (1/3 x,1/3 y) B) (0.1x, 0.1y) C) (5/6 x,5/6 y) D) (5/2 x,5/2 y)
Learn more about Dilation:
https://brainly.com/question/29449871
#SPJ4
A sports team donates 252 tickets to a sporting event, with tickets to be shared equally among 9 classrooms. How many tickets does each classroom receive?
Answers
Answer:
28 tickets
Step-by-step explanation:
252/9=28
52÷25
What is the answer :)
Answers
Answer:
2.08 this is answer
Please please help me making brainliest if correct

Answers
Answer:
It's A
Step-by-step explanation:
Because both triangles have the same side connected to, which means that that side is congruent to each other and because it tells us that JL and JK are congruent and KM and ML are congruent that means that its sss. Also, it is not giving us an angle to find the congruence so it has to be sss.
an insurance agent meets twelve potential customers independently, each of whom is equally likely to purchase an insurance product. six are interested only in auto insurance, four are interested only in homeowners insurance, and two are interested only in life insurance. the agent makes six sales. calculate the probability that two are for auto insurance, two are for homeowners insurance, and two are for life insurance.
Answers
The probability of customers buying each insurance is 1/24.
What is probability?Probability is the branch of Mathematics that deals with the measurement of the chance of occurrence of a random event.
The probability of any event always lie in the close interval of 0 and 1 [0,1].
Given that,
Total number of sales is 6.
Total number of customers is 12.
The number of customers interested only in auto insurance is 6.
The number of customers interested only in homeowners insurance is 4.
The number of customers interested only in life insurance is 2.
Now, the probability that two sales are for auto insurance is given as,
2/6 = 1/3
The probability that two sales are for homeowners insurance is given as,
2/4 = 1/2
And, the probability that two sales are for life insurance is given as,
2/4 = 1/2
Thus the probability of two sales for each insurance is given as the product of all the three probabilities as,
1/3 × 1/2 × 1/2 = 1/12
And, the probability of six customers out of 12 buying the sales is,
6/12 = 1/2
Thus, the probability for the given case is,
1/2 × 1/12 = 1/24
Hence, the probability for the given problem is 1/24.
To know more about probability click on,
https://brainly.com/question/11234923
#SPJ1
what is the minimum vertical distance between the line y=x^2 1 and y=x-x^2
Answers
The minimum vertical distance between the curves y = x^2 + 1 and y = x - x^2 is approximately 0.7937 units.
To find the minimum vertical distance between the lines y = x^2 + 1 and y = x - x^2, we can set these two equations equal to each other and solve for x:
x^2 + 1 = x - x^2
Rearranging, we get:
2x^2 - x + 1 = 0
We can use the quadratic formula to solve for x:
x = [1 ± sqrt(1 - 4(2)(1))]/(2(2))
x = [1 ± sqrt(-7)]/4
Since the discriminant of the quadratic equation is negative, the roots are imaginary and there are no real solutions for x. Therefore, the two curves do not intersect, and the minimum vertical distance between them is the shortest distance between any point on one curve and any point on the other curve.
To find this minimum distance, we can use the perpendicular distance between the curves. The line perpendicular to the curve y = x^2 + 1 at a point (a, a^2 + 1) will have a slope of -1/(2a), since the derivative of the curve at that point is 2a. Therefore, the equation of the perpendicular line is:
y - (a^2 + 1) = (-1/(2a))(x - a)
The intersection of this line with the curve y = x - x^2 will give us the point on the second curve that is closest to the first curve. Substituting y = x - x^2 into the equation of the perpendicular line, we get:
x - x^2 - (a^2 + 1) = (-1/(2a))(x - a)
Simplifying and solving for x, we get:
x = (2a^3 - 2a^2 - a + 1)/(2a^2 + 1)
Substituting this value of x back into the equation y = x - x^2, we get:
y = (2a^3 - 2a^2 - a + 1)/(2a^2 + 1) - (2a^6 - 4a^5 + 2a^4 + 1)/(4a^4 + 2a^2 + 1)
Simplifying, we get:
y = (-2a^7 + 6a^6 - 6a^5 + 3a^4 - a^3 + 2a^2 - a + 1)/(4a^4 + 2a^2 + 1)
Now, we can use calculus to find the minimum value of this expression. Taking the derivative with respect to a and setting it equal to zero, we get:
-14a^6 + 36a^5 - 30a^4 + 12a^3 - 3a^2 + 4a - 1 = 0
This equation has no closed-form solution, but we can use numerical methods to approximate the value of a that minimizes the expression. Solving this equation numerically, we get:
a ≈ 0.3538
Substituting this value of a back into the expression for y, we get:
y ≈ 0.7937
Click the below link, to learn more about vertical distance:
https://brainly.com/question/4493830
#SPJ11
4 out of 5 dentists prefer Crest. If they asked 30 dentists what tooth paste they prefer, how many did NOT PREFER Crest.
Answers
Answer:
24 would prefer CREST
6 woul NOT prefer Crest
Step-by-step explanation:
4:5=x:30
In the rainforest of Puerto Rico, I needed to measure the height of a really tall tree. I used a device to measure the angle of elevation from my line of sight to the top of a tree to be 31°. Find the height of the tree if my height is 6 feet and I was 275 feet from the tree
Answers
Answer:
Step-by-step explanation:
See image

if two lines are parallel and one has a slope of -1/7, what is the slope of the other line?
Answers
-1/7, since parallel lines have equal slopes.
If Emilie and Jessie can skateboard 4 miles in 20 minutes. How far can they go in 60 minutes?
Answers
Answer:
12 miles
Step-by-step explanation:
Answer:
12 miles
Step-by-step explanation:
20 * 3 = 60 minutes
4 * 3 = 12 miles
Hope this is helpful:)
can anyone help ?????

Answers
What is the measure of the obtuse angle? 18 54 108 216
Answers
The measure of the obtuse angle in the triangle is 108 degrees.
How to find obtuse angles of a triangle?A triangle is a polygon with three sides. The total sum of the angles in a triangle is 180 degrees.
Therefore, the measure of the obtuse angle in the triangle can be found as follows;
An obtuse angle is an angle which is greater than 90° and less than 180°.
Hence, the angles of the triangle are 1x, 3x and 6x.
3x + 1x + 6x = 180
10x = 180
x = 180 / 10
x = 18
Therefore, the obtuse angle of the triangle is 6(18) = 108 degrees.
learn more on obtuse angles here: brainly.com/question/9637024
#SPJ1

Answer:
c) 108 on edgen
If someone could help me with these two problems please.
( will mark brainliest if correct )

Answers
Answer:
1st- x=140°
2nd-x=90°
Step-by-step explanation:
The interior angle of a 9 -sided polygon is 140x9=1260
divide by 9
The interior angles of a triangle always add up to 180
90°each
I NEED HELP ON THIS, IT'S DUE IN A FEW HOURS! I WILL GIVE BRAINLIEST!

Answers
Answer:
Heres the general Idea i Got
Step-by-step explanation:
You can Connect the various shapes into traingles and rectangles . for ex : from -8 to 4 you can form a traingle. and then from B to G you can form a rectangle, From G to H by moving straight along G you can make another traingle and so on You can use your imagination to figure the total area by adding up those small figures you just made !
Case 1: Carter needs a fence with a length of 78.724 yards.
Case 2: Carter needs a grass sod with an area of 178 square yards.
How to determine the fence and grass sod area needed for a backyard
In this problem we find the representation of a backyard, which is a combinations of areas of triangles and rectangles, whose formulas are introduced below:
Rectangle
A = b · h
Triangle
A = 0.5 · b · h
Where:
b - Base, in yards.h - Height, in yards.A - Area, in square yards.The perimeter of the backyard is the sum of its sides, where oblique sides are determined by Pythagorean theorem. Now we proceed to compute for each each case:
Case 1 - Carter needs the length of the fence.
p = 8 yd + √[(10 yd)² + (6 yd)²] + 6 yd + 4 yd + 4 yd + 6 yd + 6 yd + √[(7 yd)² + (4 yd)²] + 18 yd + 7 yd
p = 78.724 yd
Case 2 - Carter needs the area of the grass sod.
A = 0.5 · (10 yd) · (6 yd) + (7 yd) · (8 yd) + (13 yd) · (6 yd) + 0.5 · (7 yd) · (4 yd)
A = 178 yd²
To learn more on areas and perimeters: https://brainly.com/question/11957651
#SPJ1
A tank is full of water. Find the work required to pump the water out of the spout. Use the fact that water weighs 62.5 lb/ft3
Answers
The work required to pump the water out of the spout is 5000ft⋅lb
Given
The volume V=12(4ft)(5ft)(6ft)=60ft3,
Then the weight is w = γV = (62.5lb /ft³) (60ft³) = 3750lb.
Since work is force × distance, you need a distance here, and the appropriate one is the distance you must raise the center of mass to get the H2O out of the spout.
Since the center of mass of a uniform triangular area is 13 of the way from any side, the distance is (4ft)/3 so the work is (3750lb) (4ft)/3=5000 ft-lb.
In calculus, the area of a horizontal section yft from the lowest point is (5ft) × (6ft) × y / (4ft) = 7.5y ft2.
We have to lift that slice 4ft−y, so work is
w = \(\int\limits^4_0\) (62.5)(4 − y) (7.5y)
dy = (62.5)[15y2−2.5y3]40 = 5000ft⋅lb
The work required to pump the water out of the spout is 5000ft-lb
Learn more about calculus here: https://brainly.com/question/24430269
#SPJ4
The elder brother has 280 yuan, and the younger brother has 56 yuan, How many times is the money of the elder brother?
Answers
Step-by-step explanation:
how many times is the money of the elder brother ?
this is the same to ask "how many times do I need to add the money of the younger brother to get the money off the older brother ?"
this is simply done by division : how many times do 56 fit into 280 ?
280 / 56 = 5
so, the elder brother has 5 times the money of the younger brother.
Answer:
56+56+56+56+56
hence
5 times
Which expression is a monomial

Answers
second one for sure
Find the constant of proportionality in the following table:
Pls be quick!

Answers
Answer:
0.2
Step-by-step explanation:
The standard form of the equation of a direct proportion is
y = kx
Substitute x and y with values from one given point, and solve for k.
0.4 = k × 2
2k = 0.4
k = 0.2
Answer: 0.2
Steven has $14.26 and buys a leash. How much money does Steven have left?
explanation PLS
Answers
Answer:
x
Explanation:
Let cost of leash = y
14.26 - y = x
Hope this helps and have a great day :)
And please mark me brainliest if you can :)
A bag contains 3 red balls and 2 blue balls if two balls were drawn at random one at a time with replacement what is the probability that the first one is red and the second one is blue.
Answers
Answer:
2/5, 1/5
Step-by-step explanation: