Rewrite the expression as a single logarithm
Please help will give brainlist only if correct!

Answers
The correct option is (d) i.e. log [ √x × (x-1)^3 / ∛ (x+1)^2 ] is as the single logarithm.
What is logarithm?
Logarithm is a mathematical operation which is used to determine the exponential power of a number. It is the inverse operation of exponentiation. Logarithm is commonly used in calculus, algebra, and other areas of mathematics. It can also be used to solve problems involving exponents, roots, and powers. Logarithm is denoted by the symbol log, and is read as "log to the base". The base is the number which the logarithm is taken to. For example, log2 10 is the logarithm to the base 2 of 10. This is equivalent to saying "2 to the power of what equals 10?" The answer is that 2 raised to the power of 3 (2^3) would equal 10.
Given, log x / 2 + 3 [ log(x-1) - 2/9 log(x+1) ]
= log √x + 3 log(x-1) - 2/3 log (x+1) {∵ log x^a = a log x }
= log √x + log (x-1)^3 - log (x+1)^2/3
= log √x + log [(x-1)^3 / (x+1)^2/3] {∵ log a - log b = log a/b }
= log [√x × (x-1)^3 / (x+1)^2/3 ]
= log [ √x × (x-1)^3 / ∛ (x+1)^2 ]
Hence, (d) is the correct option.
Learn more about Logarithm from the link given below:
https://brainly.com/question/25710806
#SPJ1
Related Questions
The figure shows a two-dimensional
representation of a bird made out of
origami paper. Find m/1 and m/2.
Explain your reasoning.
(3x + 5)°
(4x-30)

Answers
In the given origami of the two dimensional figure , the value of angle 2 is 70° and the value of angle 1 is 110 °
Parallel lines are straight lines that do not intersect at any point in geometry.
Parallel planes are three-dimensional pathways that never intersect. Parallel curves do not touch or intersect and have a fixed minimum distance.
From the figure we can see that m∠1 = 4x-30 as they are vertically opposite angles.
Again m∠1 = 3x+5 as they are corresponding angles from the pair of parallel lines.
now let us solve the linear equation to calculate the value of x.
3x+5 = 4x-30
or, -x = -35
or, x = 35
Now
m∠1 = 3x+5 = 110
Therefore m∠2 = 180 -110 = 70 ( straight angle formed whose sum is 180)
To learn more about origami visit:
https://brainly.com/question/8667656
#SPJ1
Use the normal distribution to compute probability with technology - Calculator Question Suppose that the annual household income in a region is normally distributed with mean $25,000 and standard deviation $6,000. If the poverty level for the region is at or below $12,000, what percentage of the population lives in poverty? • Round your answer to two decimal places.
Answers
Answer:
0.02
Step-by-step explanation:
Given a normal distribution :
Mean income (m) = 25000
Standard deviation of income (s) = 6000
X ≥ 12000
Using the relation to fund the standardized score :
Zscore =(x - m) / s
Zscore = ( 12000 - 25000) / 6000
Zscore = -13000 / 6000
Zscore = - 2.167
Using a z probability calculator :
P(Z ≤ - 2.167) = 0.015117
= 0.02
Tim has a collection of model cars and boats.he has 3 cars for every 2 boat. He has a total of 12 boats.
Answers
Answer:
18 cars
Step-by-step explanation:
6 times 2= 12 boats
3 times 6= 18 cars
Hopefully this helps!
Answer:
He has 36 cars if there are 12 boats
Step-by-step explanation:
If he has 3 cars for every 2 boats he has then he would have 36 cars. You multiply 12 and 3 to get 36.
you have $6.17. you buy 7 items that cost $0.76 each. how much money do you have left
Answers
Answer:
$0.85
Step-by-step explanation:
if you multiply 7x0.76=5.32
and then subtract the 6.17-5.32=$.85
Answer:
.85
Step-by-step explanation:
Multiply .76x7 then subtract 5.32 from 6.17 and you get 0.85.
The strength of an aluminum alloy is normally distributed with mean 10 gigapascals (GPa) and standard deviation 1.4 GPa. What is the first [lower] quartile of the strengths of this alloy
Answers
Answer:
The first quartile of the strengths of this alloy is 9.055 GPa.
Step-by-step explanation:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
The strength of an aluminum alloy is normally distributed with mean 10 gigapascals (GPa) and standard deviation 1.4 GPa.
This means that \(\mu = 10, \sigma = 1.4\)
What is the first [lower] quartile of the strengths of this alloy?
This is the 100/4 = 25th percentile, which is X when Z has a pvalue of 0.25, so X when Z = -0.675.
\(Z = \frac{X - \mu}{\sigma}\)
\(-0.675 = \frac{X - 10}{1.4}\)
\(X - 10 = -0.675*1.4\)
\(X = 9.055\)
The first quartile of the strengths of this alloy is 9.055 GPa.
need help these 3 math ?

Answers
Answer:
I can't see the problem, sorry.
Good morning can somebody help me out the answer choice are
A.56.4 degrees
B.40.0 degrees
C. 13.3 degrees
D. 33.6 degrees

Answers
Answer:
Option D
Step-by-step explanation:
Measure of adjacent side = 20
Measure of Hypotenuse = 24
Since, measures of adjacent side and Hypotenuse have been given in the question, cosine ratio will be applied to find the measure of angle x.
cos(x) = \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
cos(x) = \(\frac{20}{24}\)
x = \(\text{cos}^{-1}(0.833)\)
= 33.55°
≈ 33.6°
Option D is the answer.
Find the coordinates of a point A whose distance from the origin (0, 0) is 5 units.
Answers
Answer:
Two examples of points that satisfy this condition is (0,5) and (0,-5).
Step-by-step explanation:
Suppose we have two points:
\(A = (x_{1}, y_{1})\)
\(B = (x_{2}, y_{2})\)
The distance between these points is:
\(D = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}\)
In this question:
B(0,0)
A(x,y)
We have to find x and y.
We have that:
\(\sqrt{(x-0)^{2} + (y-0)^{2}} = 5\)
\(\sqrt{x^{2} + y^{2}} = 5\)
\((\sqrt{x^{2} + y^{2}})^{2} = 25\)
\(x^{2} + y^{2} = 25\)
One example of a point:
I will say that x = 0. So
\(0^{2} + y^{2} = 25\)
\(y = \pm \sqrt{25}\)
\(y = \pm 5\)
So two examples of points that satisfy this condition is (0,5) and (0,-5).
The distance formula is a formula that is used to find the distance between two points.
The coordinate of point A is (0, 5) or (0, -5).
Distance formula:Let us consider that, coordinate of point A is (x, y).
The distance between (0,0) and (x, y) is computed as by using distance formula.
\(Distance=\sqrt{(x-0)^{2}+(y-0)^{2} } \\\\5=\sqrt{(x-0)^{2}+(y-0)^{2} } \\\\x^{2} +y^{2}=25\)
All values that satisfies above equation, will be the coordinate of point A.
When x = 0,
\(y=\sqrt{25} =\pm 5\)
The coordinate of point A is (0, 5) or (0, -5).
Learn more about the distance formula here:
https://brainly.com/question/661229
Jane has a pre-paid cell phone with NextFell. She can't remember the exact costs, but her plan has a monthly fee and a charge for each minute of calling time. In June she used 370 minutes and the cost was $133.00. In July she used 530 minutes and the cost was $181.00.
A) Express the monthly cost C
C
in terms of x
x
, the number of minutes of calling time she used.
Answer: c
B) If Jane used 477 minutes of calling time in August, how much was her bill?
Answer: $
Answers
Answer:
C = 0.30x +22$165.10Step-by-step explanation:
A) Let x represent minutes used, and C represent monthly charge. We are given two (x, C) pairs: (370, 133.00) and (530, 181.00)
We can use these in the 2-point form of the equation for a line.
y = (y2 -y1)/(x2 -x1)(x -x1) +y1
C = (181 -133)/(530 -370)(x -370) +133
C = 48/160(x -370) +133
C = 0.30x -111 +133
C = 0.30x +22
__
B) For x = 477 minutes, the charge will be ...
C = 0.30(477) +22 = $165.10 . . . . for 477 minutes
The monthly cost C = $22 + $0.30x
Jane's bill for August is $165.10
The total amount Jane pays is the sum of the monthly fee and the charge per minute.
Total amount = monthly fee + charge per minute
Two equations can be derived from the question
a + 370b = 133 equation 1
a + 530b = 181 equation 2
Where:
a = monthly fee
b = charge per minute
This equation would be solved using simultaneous equation
Subtract equation 1 from equation 2
160b = 48
Divide both sides of the equation by 160
b = 48 / 160
b = 0.30
Substitute for b in equation 1
a + 370(0.30) = 133
a + 111 = 133
a = 133 - 111
a = 22
Based on the above calculations, the monthly fee is $22 and the charge per minute is $0.30
Equation for monthly cost = $22 + $0.30x
If Jane used 477 minutes, total charge :
$22 + $0.30(477) =
22 + 143.10
= $165.10
A similar question was solved here: https://brainly.com/question/17911105?referrer=searchResults
saras bookshelf is 40cm long 50 cm wide and 900 mm high she wants to paint it and calculated its volume as 180000cm3 check if theres something wrong if yes show your working for correction
ill mark u
Answers
Answer:
The volume of the bookshelf is 180000 cm³.
Step-by-step explanation:
The dimensions of the bookshelf are 40 cm, 50 cm and 900 mm.
We know that,
1 mm = 0.1 cm
900 mm = 90 cm
Now the dimensions become 40 cm, 50 cm and 90 cm.
The volume of the bookshelf can be calculated as :
V = lbh
Substitute all the values,
V = 40 cm × 50 cm × 90 cm
V = 180000 cm³
So, the volume of the bookshelf is 180000 cm³.
What reason can be used to complete this proof?
m∠1=m∠3 because ∠1≅∠3.
m∠1+m∠2=m∠CXB and m∠2+m∠3=m∠AXD _________.
m∠1+m∠2=m∠AXD because you can substitute m∠1 for m∠3.
m∠CXB=m∠AXD by the transitive property of equality.
So, ∠AXD≅∠CXB.
Answers
Answer:
Option (2)
Step-by-step explanation:
Given:
∠1 ≅ ∠3
To Prove:
∠AXD ≅ ∠CXB
Solution:
Given question is incomplete; find the complete question in the attachment.
Statements Reasons
1). m∠1 ≅ m∠3 because m∠1 ≅ m∠3 1). Given
2). m∠1 + m∠2 = m∠CXB and
m∠2 + m∠3 = m∠AXD 2). Angle addition postulate
3). m∠1 + m∠2 = m∠AXD 3). Because you can substitute
m∠1 for m∠3
4). m∠CXB = m∠AXD 4).Transitive property of equality
5). ∠AXD ≅ ∠CXB
Therefore, Option (2) will be the correct option.

Please use the following to answer the next 4 questions. A soft drink filling machine, when in perfect adjustment, fills the bottles with 12 ounces of soft drink. A random sample of 49 bottles is selected, and the contents are measured. The sample yielded a mean content of 11.88 ounces with a standard deviation of 0.35 ounces.
1.State the null and alternative hypotheses.
a. H0: µ = 0, Ha: µ > 11.88
b. H0: µ = 0, Ha: µ ≠ 11.88
c. H0: µ = 0, Ha: µ > 12
d. H0: µ = 0, Ha: µ ≠ 12
2.Specify the rejection region for = 0.01. Reject H0 if
a. t > 2.68
b. t < -2.68
c. |t| > 2.68
d. z < 2.68
3.Calculate the p-value
a. 0.01
b. 0.02
c. 0.005
d. 0.05
4. What is your conclusion?
a. Reject H0
b. Fail to reject H0
c. Reject Ha
d. Fail to reject Ha
Answers
The null and alternative hypotheses can be stated as follows:
c. H0: µ = 12, Ha: µ ≠ 12
The null hypothesis (H0) assumes that the population mean content of the bottles is 12 ounces, indicating perfect adjustment of the filling machine. The alternative hypothesis (Ha) states that the population mean content is not equal to 12 ounces, suggesting that the machine is not in perfect adjustment.
The rejection region for α = 0.01 can be specified as:
c. |t| > 2.68
This means that we would reject the null hypothesis if the absolute value of the calculated t-statistic is greater than 2.68.
To calculate the p-value, we need the t-statistic corresponding to the sample mean and standard deviation. With a sample mean of 11.88 ounces, a standard deviation of 0.35 ounces, and a sample size of 49, we can calculate the t-statistic. The p-value represents the probability of observing a sample mean as extreme as the one obtained, assuming the null hypothesis is true.
The p-value cannot be determined without the t-statistic value or the corresponding degrees of freedom.
Without the p-value, we cannot draw a definitive conclusion. To make a conclusion, we would compare the calculated t-statistic to the critical t-value based on the chosen significance level (α = 0.01). If the calculated t-statistic falls within the rejection region (|t| > 2.68), we would reject the null hypothesis. If the calculated t-statistic falls outside the rejection region, we would fail to reject the null hypothesis.
For such more question on hypotheses
https://brainly.com/question/606806
#SPJ8
At the grocery store, Abdullah purchased 3 pounds of mac and cheese for $7.50. How much mac and cheese could Abdullah buy for $20?
Answers
The number of mac and cheese Abdullah can buy for $20 is 8.
What is the unitary method?The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.
Given that, at the grocery store, Abdullah purchased 3 pounds of mac and cheese for $7.50.
Now, cost of 1 pound of mac and cheese =Total cost/Number of pounds of mac and cheese
= 7.50/3
= $2.50
Then, with $20 Abdullah can by =20/2.50
= 8
Therefore, the number of mac and cheese Abdullah can buy for $20 is 8.
To learn more about the unitary method visit:
brainly.com/question/22056199.
#SPJ1
Which sequence of transformations was applied to the parent tangent function to create the function m(x) = 2tan(3x+4)
Answers
The function m(x) = 2tan(3x+4) is obtained by applying a sequence of transformations to the parent tangent function.
To determine the sequence of transformations, let's break down the given function:
1. Inside the tangent function, we have the expression (3x+4). This represents a horizontal compression and translation.
2. The coefficient 3 in front of x causes the function to compress horizontally by a factor of 1/3. This means that the period of the function is shortened to one-third of the parent tangent function's period.
3. The constant term 4 inside the parentheses shifts the function horizontally to the left by 4 units. So, the graph of the function is shifted to the left by 4 units.
4. Outside the tangent function, we have the coefficient 2. This represents a vertical stretch.
5. The coefficient 2 multiplies the output of the tangent function by 2, resulting in a vertical stretch. This means that the graph of the function is stretched vertically by a factor of 2.
In summary, the sequence of transformations applied to the parent tangent function to create the function m(x) = 2tan(3x+4) is a horizontal compression by a factor of 1/3, a horizontal shift to the left by 4 units, and a vertical stretch by a factor of 2.
Example:
Let's consider a point on the parent tangent function, such as (0,0), which lies on the x-axis.
After applying the transformations, the corresponding point on the function m(x) = 2tan(3x+4) would be:
(0,0) -> (0,0) (since there is no vertical shift in this case)
This example helps illustrate the effect of the transformations on the graph of the function.
For more question on expression
https://brainly.com/question/1859113
#SPJ8
the weight of an apple is 150g, rounded to the nearest 5g. What is the lower bound of the weight of the apple?
What is the upper bound of the weight of the apple?
Answers
Answer:
1 answer
Answer:lower bound = 147.5gupper bound = 152.5gStep-by-step explanation:if you were rounding a single digit number to the nearest 5, ...
Step-by-step explanation:
what theorems or postulates could you use to prove this relationship

Answers
From the diagram given, we can see that line a is parallel to line b. This means that the position of each of the angle on line a is equal to the position of each of the angle in line b
From the figure <1 = <(7x+19)degree (corresponding angle). Also <5 = 7x+19 = <1 (corresponding angle as well)
From the above, we can say that <5 = <1 and since <5 and <6 lies on the same stright line, their sum will be 180.
Don't forget that <5 is now replaced as <1. Hence <1+<6 = 180 (supplementary angle).
From the expalnation above, the theorems that was used to prove the relationship between <1 and <6 are supplementary angle, corresponding angle and same side interior angle
Hence option D is correcct
Find the slope and the y-intercept of the line. 3x -4y = -12
Answers
\(\\ \sf\longmapsto 3x-4y=-12\)
Convert to y=mx+b form\(\\ \sf\longmapsto 3x+12=4y\)
\(\\ \sf\longmapsto y=\dfrac{3x+12}{4}\)
\(\\ \sf\longmapsto y=\dfrac{3}{4}x+\dfrac{12}{4)\)
\(\\ \sf\longmapsto y=\dfrac{3}{4}+3\)
Slope=3/4While starting salaries have fallen for college graduates in many of the top hiring fields, there is some good news for business undergraduates with concentrations in accounting and finance (Bloomberg Businessweek, July 1, 2010). According to the National Association of Colleges and Employers’ Summer 2010 Salary Survey, accounting graduates commanded the second highest salary at $50,402, followed by finance graduates at $49,703. Let the standard deviation for accounting and finance graduates be $6,000 and $10,000, respectively.
a. What is the probability that 100 randomly selected accounting graduates will average more than $52,000 in salary?
b. What is the probability that 100 randomly selected finance graduates will average more than $52,000 in salary?
c. Comment on the above probabilities.
Answers
Answer:
Step-by-step explanation:
According to the central limit theorem, if independent random samples of size n are repeatedly taken from any population and n is large, the distribution of the sample means will approach a normal distribution. The size of n should be greater than or equal to 30. Given n = 100 for both scenarios, we would apply the formula,
z = (x - µ)/(σ/√n)
a) x is a random variable representing the salaries of accounting graduates. We want to determine P( x > 52000)
From the information given
µ = 50402
σ = 6000
z = (52000 - 50402)/(6000/√100) = 2.66
Looking at the normal distribution table, the probability corresponding to the z score is 0.9961
b) x is a random variable representing the salaries of finance graduates. We want to determine P(x > 52000)
From the information given
µ = 49703
σ = 10000
z = (52000 - 49703)/(10000/√100) = 2.3
Looking at the normal distribution table, the probability corresponding to the z score is 0.9893
c) The probabilities of either jobs paying that amount is high and very close.
(a) The number of terms in an arithmetic progression is 40 and the last is -54. Given that the sum of the 15 terms added to the sum of the first 30 terms is zero. Calculate (1) The first term and common difference, (ii) the sum of the progression.
Answers
(i) The first term (a) is 24 and the common difference (d) is -2.
(ii) The sum of the progression is 2520.
i) Finding the first term and common difference:
Given that the number of terms in the arithmetic progression is 40 and the last term is -54, we can use the formula for the nth term of an arithmetic progression to find the first term (a) and the common difference (d).
The nth term formula is: An = a + (n-1)d
Using the given information, we can substitute the values:
-54 = a + (40-1)d
-54 = a + 39d
We also know that the sum of the first 15 terms added to the sum of the first 30 terms is zero:
S15 + S30 = 0
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values for S15 and S30:
[(15/2)(2a + (15-1)d)] + [(30/2)(2a + (30-1)d)] = 0
Simplifying the equation:
15(2a + 14d) + 30(2a + 29d) = 0
30a + 210d + 60a + 870d = 0
90a + 1080d = 0
a + 12d = 0
a = -12d
Substituting this value into the equation -54 = a + 39d:
-54 = -12d + 39d
-54 = 27d
d = -2
Now we can find the value of a by substituting d = -2 into the equation a = -12d:
a = -12(-2)
a = 24
Therefore, the first term (a) is 24 and the common difference (d) is -2.
ii) Finding the sum of the progression:
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S40 = (40/2)(2(24) + (40-1)(-2))
S40 = 20(48 - 39(-2))
S40 = 20(48 + 78)
S40 = 20(126)
S40 = 2520
Therefore, the sum of the arithmetic progression is 2520.
for such more question on common difference
https://brainly.com/question/25731911
#SPJ8
6. A company car purchased for $39,600 depreciates at 12% per annum. What is the car
worth after 3 years?
Answers
Answer:
$26,986.29
Step-by-step explanation:
We can use the formula for calculating the depreciation of an asset over time:
wor
\(\bold{D = P(1 - \frac{r}{100} )^t}\)
where:
D= the current value of the asset
P = the initial purchase price of the asset
r = the annual depreciation rate as a decimal
t = the number of years the asset has been in use
In this case, we have:
P = $39,600
r = 12% = 0.12
t = 3 years
Substituting these values into the formula, we get:
\(D= 39,600(1 - \frac{12}{100})^3\\D= 39,600(1 - 0.12)^3\\D= 39,600*0.88^3\\D= 39,600*0.681472\\D=26986.2912\)
Therefore, the car is worth approximately $26,986.29 after 3 years of depreciation at a rate of 12% per annum.
Answer:
$26,986.29
Step-by-step explanation:
As the car's value depreciates at a constant rate of 12% per annum, we can use the exponential decay formula to create a function for the value of the car f(t) after t years.
Exponential Decay formula\(\boxed{f(t)=a(1-r)^t}\)
where:
f(t) is the value of the car (in dollars) after t years.a is the initial value of the car.r is the depreciation rate (as a decimal).t is the time period (number of years after purchase).In this case, the initial value is $39,600, and the rate of depreciation is 12% per year. Therefore, the function that models the value of the car after t years is:
\(f(t)=39600(1-0.12)^t\)
\(f(t)=39600(0.88)^t\)
To calculate the value of the car after 3 years, substitute t = 3 into the function:
\(\begin{aligned} f(3)&=39600(0.88)^3\\&=39600(0.681472)\\&=26986.2912\\&=26986.29\;(\sf 2\;d.p.)\end{aligned}\)
Therefore, the car is worth $26,986.29 after 3 years.
Find the x- and y- intercepts of each equation.
y = -2x + 7

Answers
Answer:
y-intercept: (0,7)
x-intercept: (3.5,0)
Step-by-step explanation:
The equation is in slope-intercept form.
\(y = mx + b\\\rule{150}{0.5}\\m - \text{slope}\\b - \text{y-intercept}\)
Since '7' is in b's spot, it is the y-intercept of the equation.
(0,7)
To find the x-intercept, we would plug 'y' in for 0 and solve for x.
\(y = -2x + 7\\\rule{150}{0.5}\\0 = -2x + 7\\\\0 - 7 = -2x + 7 - 7\\\\-7 = -2x\\\\\frac{-7=-2x}{-2}\\\\\boxed{x = 3.5}\)
The x-intercept is (3.5, 0).
Hope this helps.
Fred buys flags from a manufacturer for f dollars each and then sells the flags in his store for a 26%markup.

Answers
Answer:
the markup is 1.26 (the amount added is .26)
1.26x (when x is the price Fred buys them for from the manufacturer)
1.26(40)
$50.40 is the retail price
50.4-40
$10.40 is the markup
Step-by-step explanation:
The 26% markup means that he is selling the flags 26% above the cost.
So, the cost would represent 100%, which is 1, and 26% of markup in decimal number is 0.26.
The price including the markup would be 1.26 as decimal or 126% as percentage.
The problem states that the cost is unknown, so we represent that with a variable x. The retail price would be 1.26x, which is 126% per flag.
Finally, if Fred paid $40 per flag, the actual retail price would be:
1.26($40)=$50.40.
With $10.40 of markup.
The dimensions of a trapezoid are halved.
a) How will the area be affected?
b) If the area of the original trapezoid is 28 cm?, then what will the area of the smaller
trapezoid be?
Draw or add images here
Answers
Answer:
a) area will be 1/4 of the original
b) 7 cm²
Step-by-step explanation:
a)Consider the equation for the area of a trapezoid:
A = 1/2(b1 +b2)h
Now, halve each of the dimensions:
A' = 1/2((1/2)b1 +(1/2)b2)((1/2)h)
A' = (1/4)(1/2(b1 +b2)h) = 1/4A
The area is multiplied by the square of the scale factor: (1/2)² = 1/4.
__
b)The area of the smaller trapezoid will be ...
A' = 1/4A = (1/4)(28 cm²) = 7 cm²

I WILL MARK BRAINIEST
Please help asap it’s due

Answers
7x-8=90
7x=98
x=14
A number between 10 and 100 is four times the sum of its digits. If the product of two digits is 8, find the sum of digits of the number.
Answers
Answer:
24 is the number. The sum of its digits is 6.
Step-by-step explanation:
There are four two-digit numbers the product of whose digits is 8: 18, 24, 42, and 81. Of these numbers, 24 is four times the sum of its digits:
24 = 4 × 6 = 4 × (2 + 4)
is a number that is____________
a multiple of two or more numbers.
Answers
A number that can only be divided by 1 or 0 is prime. A composite number is a number that can be divided by 0, 1, 2, etc. I couldn't really get the question that you were trying to type, but this is what I came up with.
Hope this helps and just remember you are loved!
Two sides of a triangle have lengths 13 m and 19 m. The angle between them is increasing at a rate of 2°/min. How fast is the length of the third side increasing when the angle between the sides of fixed length is 60°? (Round your answer to three decimal places.)
Answers
Answer:
The third side is increasing at an approximate rate of about 0.444 meters per minute.
Step-by-step explanation:
We are given a triangle with two sides having constant lengths of 13 m and 19 m. The angle between them is increasing at a rate of 2° per minute and we want to find the rate at which the third side of the triangle is increasing when the angle is 60°.
Let the angle between the two given sides be θ and let the third side be c.
Essentially, given dθ/dt = 2°/min and θ = 60°, we want to find dc/dt.
First, convert the degrees into radians:
\(\displaystyle 2^\circ \cdot \frac{\pi \text{ rad}}{180^\circ} = \frac{\pi}{90}\text{ rad}\)
Hence, dθ/dt = π/90.
From the Law of Cosines:
\(\displaystyle c^2 = a^2 + b^2 - 2ab\cos \theta\)
Since a = 13 and b = 19:
\(\displaystyle c^2 = (13)^2 + (19)^2 - 2(13)(19)\cos \theta\)
Simplify:
\(\displaystyle c^2 = 530 - 494\cos \theta\)
Take the derivative of both sides with respect to t:
\(\displaystyle \frac{d}{dt}\left[c^2\right] = \frac{d}{dt}\left[ 530 - 494\cos \theta\right]\)
Implicitly differentiate:
\(\displaystyle 2c\frac{dc}{dt} = 494\sin\theta \frac{d\theta}{dt}\)
We want to find dc/dt given that dθ/dt = π/90 and when θ = 60° or π/3. First, find c:
\(\displaystyle \begin{aligned} c &= \sqrt{530 - 494\cos \theta}\\ \\ &=\sqrt{530 -494\cos \frac{\pi}{3} \\ \\ &= \sqrt{530 - 494\left(\frac{1}{2}\right)} \\ \\&= \sqrt{283\end{aligned}\)
Substitute:
\(\displaystyle 2\left(\sqrt{283}\right) \frac{dc}{dt} = 494\sin\left(\frac{\pi}{3}\right)\left(\frac{\pi}{90}\right)\)
Solve for dc/dt:
\(\displaystyle \frac{dc}{dt} = \frac{494\sin \dfrac{\pi}{3} \cdot \dfrac{\pi}{90}}{2\sqrt{283}}\)
Evaluate. Hence:
\(\displaystyle \begin{aligned} \frac{dc}{dt} &= \frac{494\left(\dfrac{\sqrt{3}}{2} \right)\cdot \dfrac{\pi}{90}}{2\sqrt{283}}\\ \\ &= \frac{\dfrac{247\sqrt{3}\pi}{90}}{2\sqrt{283}}\\ \\ &= \frac{247\sqrt{3}\pi}{180\sqrt{283}} \\ \\ &\approx 0.444\text{ m/min}\end{aligned}\)
The third side is increasing at an approximate rate of about 0.444 meters per minute.
9514 1404 393
Answer:
0.444 m/min
Step-by-step explanation:
I find this kind of question to be answered easily by a graphing calculator.
The length of the third side can be found using the law of cosines. If the angle of interest is C, the two given sides 'a' and 'b', then the third side is ...
c = √(a² +b² -2ab·cos(C))
Since C is a function of time, its value in degrees can be written ...
C = 60° +2t° . . . . . where t is in minutes, and t=0 is the time of interest
Using a=13, and b=19, the length of the third side is ...
c(t) = √(13² +19² -2·13·19·cos(60° +2t°))
Most graphing calculators are able to compute a numerical value of the derivative of a function. Here, we use the Desmos calculator for that. (Angles are set to degrees.) It tells us the rate of change of side 'c' is ...
0.443855627418 m/min ≈ 0.444 m/min
_____
Additional comment
At that time, the length of the third side is about 16.823 m.
__
c(t) reduces to √(530 -494cos(π/90·t +π/3))
Then the derivative is ...
\(c'(t)=\dfrac{494\sin{\left(\dfrac{\pi}{90}t+\dfrac{\pi}{3}\right)}\cdot\dfrac{\pi}{90}}{2\sqrt{530-494\cos{\left(\dfrac{\pi}{90}t+\dfrac{\pi}{3}}}\right)}}}\\\\c'(0)=\dfrac{247\pi\sqrt{3}}{180\sqrt{283}}\approx0.443855...\ \text{m/min}\)

If the present value of an item is P and we experience an inflation rate of r, which is compounded continuously, for t years, what will the future value of the item be?
P = $60
r = 4.75%
t = 5
Answers
Answer:
I think it is p= $60
PLEASE HELP
Graph the following exponential function. Show work in how you find the y intercept, talk about the end behavior, and state if it is a growth or decay function. See image.
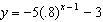
Answers
The y-intercept of the function is -9,25
How to graph the function?The function is given as:
\(y = -5(.8)^{x - 1} - 3\)
See attachment for the graph of the function
From the graph, we have the following highlights:
y-intercept = -9,25As x increases, y approaches -3As x decreases, y approaches negative infinityRead more about exponential functions at:
https://brainly.com/question/2456547
#SPJ1

Evaluate the expression
(16 + 14) +9
Answers
Answer:
39
Step-by-step explanation: