reClassify the sequence (4.) = {1,24,5,28,...) as arithmetic, geometric, or neither. If there is not enough information to classify the sequence, choose not enoughnformationO A arithmeticOB. geometricOC neitherOD. not enough information

Answers
An arithmetic sequence is a sequence of numbers in which each successive term increases or decreases by a constant value, called the common difference.
A geometric sequence is one in which each successive term of the series is obtained by multiplying the previous term by a constant value called the common ratio.
In the series below:
\(\mleft\lbrace a_n\mright\rbrace\text{ = }\mleft\lbrace1,\text{ 24, 5, 28,}\ldots\mright\rbrace\)first term = 1
second term = 24
third term = 5
fourth term = 28
Common difference d:
The difference between the second and first terms must be equal to the difference between the third and the second term.
\(\begin{gathered} d\text{ = second term - first term} \\ =\text{ 24 -1} \\ d\text{ = 23} \end{gathered}\)\(\begin{gathered} d\text{ = third term - second term} \\ =5-24 \\ d\text{ = -19} \end{gathered}\)Since the common differences obtained above are not equal, the sequence is thus not an arithmetic sequence.
Common ratio r:
The common ratio between the second and the first term must be equal to the common ratio between the third and the second term.
\(\begin{gathered} r\text{ = }\frac{\sec ond\text{ term}}{first\text{ term}} \\ =\frac{24}{1} \\ \Rightarrow r=24 \end{gathered}\)\(\begin{gathered} r=\frac{third\text{ term}}{\sec ond\text{ term}} \\ =\frac{5}{24} \\ \Rightarrow r=0.208 \end{gathered}\)Since the common ratios obtained above are not equal, the sequence is thus not a geometric sequence.
Hence, the sequence is neither an arithmetic sequence nor a geometric sequence.
The correct option is C.
Related Questions
Oliver and Chen both write down a number. Oliver says, my number has 8 hundreds and Chen's number only has 3 hundreds my number must be bigger. Oliver is not correct. explain why
Answers
Oliver's number is bigger than that of Chen.
What are hundreds in a number?It is a number equal to 10 times 10.
Given is that Oliver and Chen both write down a number. Oliver says, my number has 8 hundreds and Chen's number only has 3 hundreds, my number must be bigger.
Oliver number can be written as follows -
8 x 10 x 10
Chens number can be written as follows -
3 x 10 x 10
It can be concluded that Oliver's number is bigger than that of Chen.
Therefore, Oliver's number is bigger than that of Chen.
To solve more questions on ones and hundreds, visit the link below
https://brainly.com/question/29255057
#SPJ9
Please help
Graph the piecewise function.

Answers
Answer:
See attached
Step-by-step explanation:
The graph is attached

Consider the system of equations and the partial solution below.
6x+3y=9
5x+4y=10
Multiply the first equation by -4.
Multiply the second equation by 3.
Add the resulting system of equations.
Which terms will cancel when you add the resulting system of equations?
-36 and 36
-24x and 24x
O-15x and 15x
-12y and 12y
Answers
-15x and 15x is the answer
Answer:
-12y and 12y
Step-by-step explanation:
lets do the multiplication to each equation
\(\left \{ {{(6x+3y)(-4)=9(-4)} \atop {(5x+4y)3=10(3)}} \right.\)
this is
\(\left \{ {{-24x-12y=-36} \atop {15x+12y=30}} \right.\)
if we add the systems notice the values that do cancel are -12y and 12y
and the results of the adition is
\(-9x=-6\)
from this
\(x=\frac{-6}{-9} =\frac{2}{3}\)
and you can find y from any of the first equation.
\(y=3-2x=3-\frac{4}{3} =\frac{5}3}\)
There are spiders and dogs in Veronica's backyard. Veronica sees 240 legs in total. The total number of animals (spiders and dogs) is 3 times the amount of spiders. How many spiders are in the backyard?

Answers
There are 15 spiders in the backyard. The correct option is D
To solve this problemLet's begin by resolving the issue using algebra. Let's use "s" for the quantity of spiders and "d" for the quantity of dogs in the backyard.
As a result of the difficulty, we know that there are 3 times as many animals as there are spiders.
s + d = 3s
Simplifying this equation, we get:
d = 2s
We also know that there are 240 legs in the backyard, with each dog having 4 legs and each spider having 8. Thus, we can create the following equation:
8s + 4d = 240
Substituting d = 2s, we get:
8s + 4(2s) = 240
Simplifying and solving for s, we get:
16s = 240
s = 15
Therefore, there are 15 spiders in the backyard.
Learn more about algebra here : brainly.com/question/6143254
#SPJ1
A pair of dice are tossed twice. Find the probability that the first roll is a total of at least 5 and the second roll is a total of at least 4.
Answers
The probability that the first roll is a total of at least 5 and the second roll is a total of at least 4 is 0.764 or 76.4%.
What is the probability?The probability is the chance that an expected event occurs out of many possible events.
For two independent events happening, we use the rule of multiplication of independent events based on dice probabilities.
The event that the first roll is a total of at least 5 = A
In the event that the second roll is a total of at least 4 = B
The number of faces on each die, n = 6
The probability of event A = ³⁰/₆ = ⁵/₆
The probability of event B = ³³/₃₆ = ¹¹/₁₂
Multiplying the two probabilities, P(A) and P(B) = ⁵/₆ × ¹¹/₁₂
= ⁵⁵/₇₂ = 0.764
Thus, there is a ⁵⁵/₇₂ or 0.764 chance that the first roll is at least 5 and the second roll is at least 4.
Learn more about dice probabilities at https://brainly.com/question/23955312.
#SPJ1
Mark wants to be a chef someday and would like to start learning to grow his own
ingredients in a garden. His mom gives him 12 square feet of space in the back yard to plant
a garden. He marks off % of it to save for a tomato plant and has the rest to use for onions.
Each onion bulb needs square feet of room to grow. How many onion bulbs can he
plant?
Answers
The area of the space available for onions is:n12 square feet - 0.12x square feet. number of onion bulbs Mark can plant is: (12 - 0.12x) / y
What is percentage?
Percentage is a way of expressing a number or proportion as a fraction of 100. It is represented by the symbol "%".
Mark has marked off a certain percentage of the 12 square feet to save for a tomato plant, which means the remaining space will be used for onions.
Let's say Mark marks off x% of the space for the tomato plant. That means he will have (100-x)% of the space for onions.
The area of the space reserved for the tomato plant is:
12 square feet x (x/100) = 0.12x square feet
The area of the space available for onions is:
12 square feet - 0.12x square feet
Let's say each onion bulb needs y square feet of room to grow. Mark can plant as many onion bulbs as can fit in the remaining space, which is:
(12 square feet - 0.12x square feet) / y
So the number of onion bulbs Mark can plant is:
(12 - 0.12x) / y.
To learn more about percentage from the given link:
https://brainly.com/question/29306119
#SPJ1
4 cm
1
1
1
1
1
4 cm
/
5 cm
What is the volume of the solid?
Answers
Answer:
I don't know what you are asking.
cindy throws one red and one blue dice. find the probability that the sum of the two dice is less than 4.
Answers
The probability that the sum of the two dice is less than 4 is 3/36, which simplifies to 1/12.
What is dice probability?Dice probability refers to the likelihood of a certain outcome when rolling one or more dice. The probability of rolling a particular number on a fair six-sided die, for example, is 1 in 6 or approximately 16.67%. The probability of rolling any number from 1 to 6 on a single die is always the same since each face has an equal chance of landing face up.
Given by the question.
To finds the probability that the sum of the two dice is less than 4, we need to list all the possible outcomes when Cindy throws one red and one blue dice, and then count the number of outcomes that satisfy the condition.
Possible outcomes when throwing two dice:
Red Blue
1 1
1 2
1 3
1 4
1 5
1 6
2 1
2 2
2 3
2 4
2 5
2 6
3 1
3 2
3 3
3 4
3 5
3 6
4 1
4 2
4 3
4 4
4 5
4 6
5 1
5 2
5 3
5 4
5 5
5 6
6 1
6 2
6 3
6 4
6 5
6 6
There are 36 possible outcomes when throwing two dice.
Outcomes where the sum of the two dice is less than 4:
Red Blue
1 1
1 2
2 1
There are 3 outcomes where the sum of the two dice is less than 4.
To learn more about probability:
https://brainly.com/question/23653224
#SPJ1
Coursera gradient descent is an algorithm for finding values of parameters w and b that minimize the cost function j. True or False
Answers
Gradient Descent, a first-order iterative optimization algorithm. That means growing up. It is true.
The learning factor is always a positive number, so if you subtract W from a negative number, you get a new larger (more positive) W value.
The most popular optimization algorithm in machine learning and deep learning is gradient descent. It is a first-order optimization algorithm. This means that only the first derivative is taken into account when updating the parameters.
Gradient Descent (GD) is a first-order iterative optimization algorithm used to find the local minimum/maximum of a given function. This method is commonly used in machine learning (ML) and deep learning (DL) to minimize cost/loss functions (such as linear regression).
To know more about Gradient descent ,
brainly.com/question/30561031
#SPJ4
If the prime factorization of 600 is 2 x 2 × 2 × 3 × 5 × 5, what would you need to multiply it by to get the prime factorization of 3000?
Answers
To get the Prime factorization of 3000 we need to multiply by 5.
What is Prime Factorization:When the number is factored using prime numbers, or primes, the process is known as prime factorization. The easiest method to determine the prime factors of a given number is to keep dividing the given number by the prime factors until we will get 1.
For example, the Prime factorization of 45 is given below
=> 45/5 = 9, 9/3 = 3, 3/3 = 1
=> 45 = 5 × 3 × 3
Here we have
The prime factorization of 600 is 2 x 2 × 2 × 3 × 5 × 5
Let us assume that on multiplying with p,
we will get the factorization of 3000
=> 2 x 2 × 2 × 3 × 5 × 5 × p = 3000
=> p = \(\frac{3000}{2\times 2 \times 2 \times 3 \times 5 \times 5}\)
Her 2 x 2 × 2 × 3 × 5 × 5 = 600
=> p = \(\frac{3000}{600}\)
=> p = 5
Therefore,
To get the Prime factorization of 3000 we need to multiply by 5.
Learn more about Prime factorization at
https://brainly.com/question/9523814
#SPJ9
In the diagram below of triangle � � � GHI, � J is the midpoint of � � ‾ GI and � K is the midpoint of � � ‾ HI . If � � = − 6 � + 47 JK=−6x+47, and � � = − 2 � + 34 GH=−2x+34, what is the measure of � � ‾ JK ?
Answers
Therefore , the solution of the given problem of triangle comes out to be section J K's measure is 11 units.
What precisely is a triangle?Since a triangle has four or so more sections, it is a polygon. It has an easy rectangular form. Triangle ABC refers to a rectangle with edges A, B, and C. A single plane and cube are produced by Euclidean geometry when the sides are really not collinear. A triangle is a polygon if it has 3 components and three angles. Where a triangle's three edges come together are known as the corners. A triangle's sides add up to 180 degrees.
Here,
GJ = JI is known because J is the middle of segment GI. Similarly, we conclude that HK = KI because K is the center of section HI. Consequently, we can write:
HK = KI, GJ = JI.
Since J is the middle of GI and K is indeed the midpoint of HI, we also realize that GH = 2JK. With the provided formulas in place of GH as well as JK, we obtain:
=> -2x + 34 = 2(-6x + 47)
When we simplify and find x, we obtain:
=> -2x + 34 = -12x + 94
=> 10x = 60
=> x = 6
Now that we know how long section JK is,
JK = -6x + 47\s= -6(6) + 47\s= 11
Therefore, section J K's measure is 11 units.
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
f(x)=3x 2 +16 Find f(-1)
Answers
Answer:
X-18/3
Step-by-step explanation:
Assuming you meant 3x+18
The inverse f(-1) of the equation is above.
3.21 x 10^4 in standard notation
Answers
Answer:
32100
Step-by-step explanation:
hope this helps
sorry if its wrong
4 places to the right.
32100
Please help me I’ve been struggling

Answers
Answer:
147cm³
Step-by-step explanation:
Bottom rectangular prism: 3x4x6=72
Top rectangular prism: 5x5x3=75
72+75=147cm³
Given f(x) = 3x^3+kx-13, and x-1 is a factor of f(x), then what is the value of k?
Answers
Answer: k=10
Step-by-step explanation:
Given (x – 7)2 = 36, select the values of x. x = 13 x = 1 x = –29 x = 42
Answers
Answer:
x = 1 , x = 13
Step-by-step explanation:
(x - 7)² = 36 ( take square root of both sides )
x - 7 = ± \(\sqrt{36}\) = ± 6 ( add 7 to both sides )
x = 7 ± 6
then
x = 7 - 6 = 1
x = 7 + 6 = 13
If 20% of the people in a small town are voters and there are 2360 voters what is the population of the town
Answers
Answer:
I think its 472.
Step-by-step explanation:
The population of the town is 11,800 people.
Hope it helps ! :3
Can someone please hope and show the work?

Answers
Answer: 16 pounds of grain.
Step-by-step explanation: 36 divided by 9 is 4, which means we have to multiply bin C by how much bin J was multiplied by, which is 4, so 4x4 is 16.
(let me know if you would like me to explain more on this)
(b) Suppose CG = 3 in., CH = 2 in. and GE = 5 in. Is it possible to find the length of DH? If so, show how
to find the length. If not, explain why not.
Answers
When CG = 3 in., CH = 2 in. and GE = 5 in. the information made available in the question is not enough to solve for DH
What are similar triangles?This is a term used in geometry to mean that the respective sides of the triangles are proportional and the corresponding angles of the triangles are congruent
Examining the figure, shows that lines GH and DE should be parallel to create similar triangles
For similar triangles the sides are proportional and this can be used to solve for DH using the equation below'
CG / CE = CH / CD
Learn more about similar triangles here:
https://brainly.com/question/29333623
#SPJ1
The complete question is attached

x − 6 = -4 what is the solution
Answers
Step-by-step explanation:
\(x - 6 = - 4 \\ \\ \implies \: x = - 4 + 6 \\ \\ \implies \: x = 2\)
Answer:
2
Step-by-step explanation:
because if you substitute 2-6 you will get negative 4
\(\sqrt{2x} + 3 = 8\)2 x + 3 = 8
Answers
Answer: x= 6241/2
Step-by-step explanation:
Solve 2-3 cos x=5+3 cosx for 0° ≤ 180°
Answers
The equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
1. Start with the given equation: 2-3cos(x) = 5+3cos(x).
2. Subtract 3cos(x) from both sides to isolate the constant term: 2-3cos(x) - 3cos(x) = 5.
3. Combine like terms: 2-6cos(x) = 5.
4. Subtract 2 from both sides: -6cos(x) = 3.
5. Divide both sides by -6: cos(x) = -1/2.
6. To find the solutions for cos(x) = -1/2 in the range of 0° to 180°, we need to determine the angles where cos(x) equals -1/2.
7. These angles are 120° and 240°, as cos(120°) = cos(240°) = -1/2.
8. However, the given equation states that 2-3cos(x) equals 5+3cos(x), which is not satisfied by cos(x) = -1/2.
9. Therefore, the equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
For more such questions on equation, click on:
https://brainly.com/question/17145398
#SPJ8
Random variable X has a normal distribution with mean u and standard deviation 2. The pdf f(x) of X satisfies the following conditions: (A) f6 > f(16), (B) f(1)
Answers
As per the standard deviation, the probability of 8≤ X < 11 is 0.1429.
A random variable X is a mathematical representation of the possible values that a random process or experiment can take on. X has a normal distribution, meaning that its distribution follows a bell-shaped curve.
The standard deviation measures how spread out the values of X are around the mean.
If X has a mean of μ and a standard deviation of 2, then 68% of the values of X will fall within one standard deviation of the mean.
This means that about 68% of the values of X will fall between μ-2 and μ+2.
To find the probability that X falls between 8 and 11, we need to use the cumulative distribution function (CDF).
Using the standard normal distribution table, we find that P(X < 8) = 0.8413 and P(X < 11) = 0.9842.
Thus, the probability that 8≤ X < 11 is
=> 0.9842 - 0.8413 = 0.1429,
which rounded off to the 4th decimal place is 0.1429.
Complete Question:
Random variable X has a normal distribution with mean μ and standard deviation 2. The pdf f(x) of X satisfies the following conditions: (A) f(6) > f(16), (B) f(1) < f(17). When u is an integer, what is P(8≤ X < 11) (round off to the 4th decimal place)?
To know more about standard deviation here.
https://brainly.com/question/16555520
#SPJ4
Please help really urgent

Answers
Answer:
0.0909
Step-by-step explanation:
4 blue + 5 red + 3 black = 12 chips in total.
p=probability
1st draw:
p (blue) = 4/12
there are now 11 chips in the bag, 4-1 =3 are blue.
2nd draw?
p (blue) = 3/11
probability of pulling one blue chip followed by another blue chip is:
(4/12) X (3/11) = (4X3)/12X11)
= (12)/(132)
= 1/11
0.0909
a) Find the ratio of the number of boys to the number of girls in a class if the number of boys is
115 and that of girls is 46.
Answers
Answer:
5/7
Step-by-step explanation:
First calculate the total number of students:
Girls + boys
= 46 + 115
= 161
Then divide the number of boys over all students
= 115/161
= 5/7
PLEASE HELP I WILL MARK BRAINLIST
What is the polynomial function in standard form with zeros -10,0,2?
a) x^3 + 8x^2 + 20x
b) x^3 + 8x^2 - 20x
c) x^2 +8x -20
d) x^2 + 8x + 20
Answers
Answer:
x³ - 8x² - 20x
Step-by-step explanation:
Zeroes: 10, 0, -2
Factors are: (x - 10), (x - 0), (x + 2)
Multiply all factors to get expression:
(x - 10)x(x + 2) = x(x - 10)(x + 2)
= x(x² - 10x + 2x - 20)
= x(x² - 8x - 20)
= x³ - 8x² - 20x
The amount of a radioactive isotope present at time t is given by A(t) = 500e^ -0.028171
grams.
How many grams remain after 40 years?
Answers
According to the radioactive isotope disintegration model, the remaining mass of the radioactive isotope after 40 years is approximately equal is 129.622 grams.
What is the amount of the mass of a radioactive isotope after a period of 40 years?
The deceasing exponential expression described in the statement models the mass of the radioactive isotope (m), in grams, as a function of time (t), in years, which represents the solution of an ordinary differential equation that represents a simple disintegration.
Now, we need to evaluate the function at t = 40 to find the amount remaining after 40 years:
A(40) = 500 · exp(- 0.028171 · 40)
A(40) = 129.622
To learn more on radioactive decay: https://brainly.com/question/2028971
#SPJ1
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
this questions is reallly complicated can u please solve it
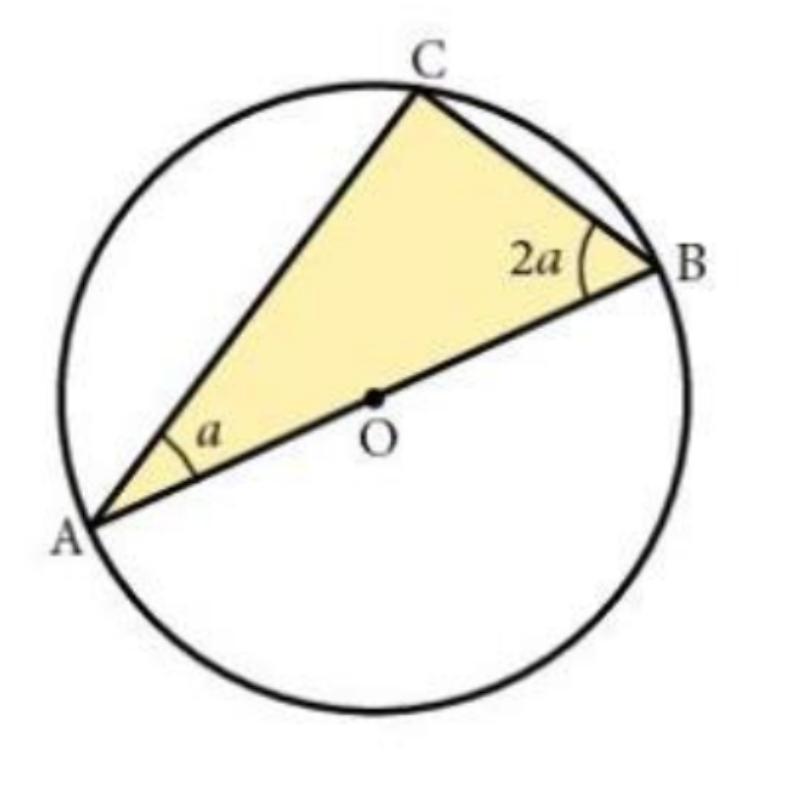
Answers
The measure of angle a is determined as 30 degrees.
What is the measure of angle a?The measure of angle a is calculated by applying the following circle theorem as follows;
If line AB is the diameter of the circle, then angle ACB will be equal to 90 degrees.
The value of a is calculated as;
a + 2a = 90 (complementary angles sum up to 90 degrees since angle ACB is equal to 90 degrees)
3a = 90
divide both sides by 3;
3a/3 = 90 / 3
a = 30
Thus, the measure of angle a is calculated by applying the following circle theorem for complementary angles.
Learn more about complementary angles here: https://brainly.com/question/16281260
#SPJ1
The bar graph shows the height of a plant each month for four months. Your friend concludes that the height of the plant in Month 4 is 3
times its height in Month 1. Is this conclusion accurate? Explain.

Answers
Answer:
I can't see the pic or I can't answer sorry
Step-by-step explanation: