QUESTION 8
Simplify 6a+ (-12b) - 9b+8a
O 2a + 3b
O 14a-21b
O2a-21b
O 14a + 3b

Answer:

Multiply 2.9 by 102.

295.8

Step-by-step explanation:

please........

Step-by-step explanation:

x = 3

y = - 2

z = 6

\(7xyz\)

Solution,

= 7 × 3 ( - 2 ) × 6

= 21 ( - 2 ) × 6

= - 42 × 6

= - 252

hence the answer is - 252....

Answer: b

Step-by-step explanation:

Answer:

-2 11/12 is the answer for me

The probability of drawing a king from a standard deck of 52 cards is 1/13.

In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.

To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).

The total number of possible outcomes is 52 because there are 52 cards in the deck.

The favorable outcomes, in this case, are the four kings.

Therefore, the probability of drawing a king is given by:

Probability = (Number of favorable outcomes) / (Number of possible outcomes)

= 4 / 52

= 1 / 13

Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.

This means that out of every 13 cards drawn, on average, one of them will be a king.

It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.

Each draw is independent, and the probability of drawing a king is constant.

For similar question on probability.

https://brainly.com/question/7965468  

#SPJ8

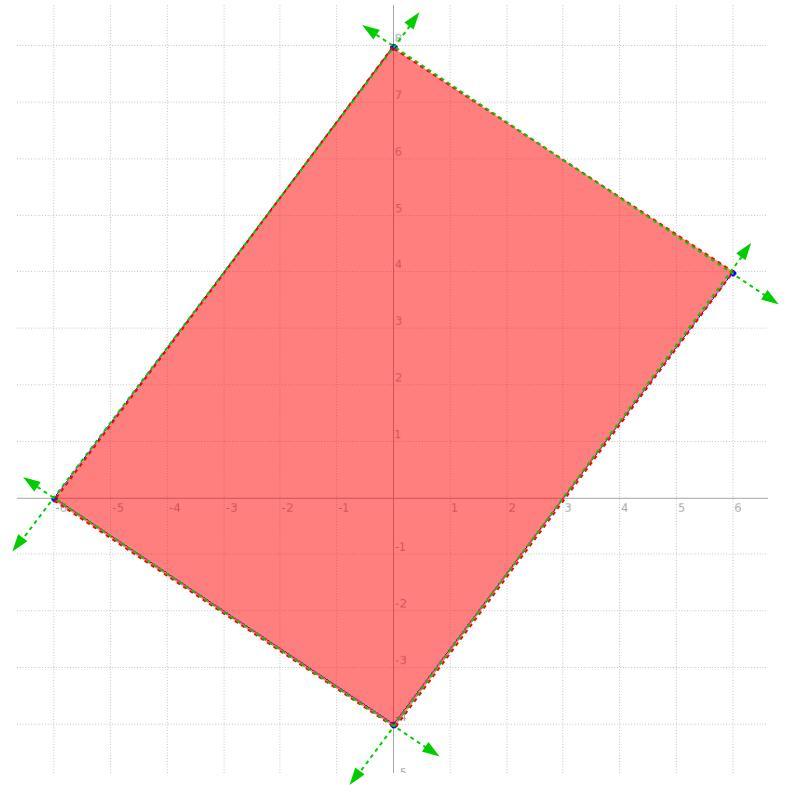
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.

we have a line passing through (-6,0) and (0,8), side one

we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two

we have a line passing through (0,-4) and (6,4), side three

now, side four is simply the line connecting one and three.

the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?

well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.

\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)

\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)

\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)

\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)

now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to  (-3 , 4).  Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.

now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality

\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)

The number of minutes spent higher than 38 meters above the ground on the Ferris wheel ride is approximately 1.0918 minutes.

To solve this problem, we need to determine the angular position of the Ferris wheel when it is 38 meters above the ground.

The Ferris wheel has a diameter of 50 meters, which means its radius is half of that, or 25 meters.

When the Ferris wheel is at its highest point, the radius and the height from the ground are aligned, forming a right triangle.

The height of this right triangle is the sum of the radius (25 meters) and the platform height (4 meters), which equals 29 meters.

To find the angle at which the Ferris wheel is 38 meters above the ground, we can use the inverse sine (arcsine) function.

The formula is:

θ = arcsin(h / r)

where θ is the angle in radians, h is the height above the ground (38 meters), and r is the radius of the Ferris wheel (25 meters).

θ = arcsin(38 / 29) ≈ 1.0918 radians

Now, we know the angle at which the Ferris wheel is 38 meters above the ground.

To calculate the time spent higher than 38 meters, we need to find the fraction of the total revolution that corresponds to this angle.

The Ferris wheel completes one full revolution in 2 minutes, which is equivalent to 2π radians.

Therefore, the fraction of the revolution corresponding to an angle of 1.0918 radians is:

Fraction = θ / (2π) ≈ 1.0918 / (2π)

Finally, we can calculate the time spent higher than 38 meters by multiplying the fraction of the revolution by the total time for one revolution:

Time = Fraction \(\times\) Total time per revolution = (1.0918 / (2π)) \(\times\) 2 minutes

Calculating this expression will give us the answer in minutes.

For similar question on diameter.

https://brainly.com/question/28162977

#SPJ8

Answer:

the answer is monkey epaulets monkey

Step-by-step explanation:

123

Answer:

One ticket cost $10.90.

Step-by-step explanation:

The total spent was $98.50--food, drinks, admission--everything.

$44.00 was for food and drinks.

We can take the 44 away from the total.

98.50 - 44.00

= 54.50

They spent 54.50 on 5 tickets to get in. Divide to find the cost of one tickets. This assumes that all 5 tickets were the same price.

54.50 ÷ 5 = 10.90



The price of one ticket was $10.90

To make this look like algebra class...

let x = the price of one ticket

5x = the price of 5 tickets

5x + 44 = 98.50

subtract 44

5x = 54.50

divide by 5

x = 10.90

The table shows a function that is decreasing over the interval (−2, 0) is option C: A 2-column table with 4 rows.  The first column is labeled x with entries negative 3, negative 2, negative 1, 0. The second column is labeled f of x with entries 2, 0, negative 10, negative 24.

The function is decreasing over the interval (-2, 0) because as the input x increases from -2 to 0, the output f(x) decreases. We can see this by looking at the values in the second column of the table:

When x = -2, f(x) = 0

When x = -1, f(x) = -10

When x = 0, f(x) = -24

Therefore, As x increases from -2 to 0, f(x) decreases from 0 to -24, which means the function is decreasing over the interval (-2, 0).

Learn more about function  from

https://brainly.com/question/17029282

#SPJ1

Answers:

==========================================

Explanation:

Answer:

Simply put, algebra is about finding the unknown or putting real life variables into equations and then solving them. ... Algebra can include real numbers, complex numbers, matrices, vectors, and many more forms of mathematic representation

Step-by-step explanation:

Answer:

Step-by-step explanation:

f(x) = -4x + 5

To find f(2) , substitute the value of x that's 2 into f(x). That is for every x in f(x) replace it with 2

That's

f(2) = - 4(2) + 5 = - 8 + 5

We have the final answer as

Hope this helps you

Answer:

B

Step-by-step explanation:

f(x) = -4x + 5

f(2) = -4(2) + 5

f(2) = -8 + 5

f(2) = -3

Best of Luck!

Answer:

\(x = \frac{1}{3} \)

Step-by-step explanation:

*Move terms to the left and set equal to zero:

4㏒(√x) - ㏒(3x) - ㏒(x²) = 0

*simplify each term:

㏒(x²) - ㏒(3x) - ㏒(x²)

㏒(x²÷x²) -㏒(3x)

㏒(x²÷x² / 3x)

*cancel common factor x²:

㏒(\(\frac{1}{3x}\))

*rewrite to solve for x :

10⁰ = \(\frac{1}{3x}\)

1 = \(\frac{1}{3x}\)

1 · x = \(\frac{1}{3x}\) · x

1x = \(\frac{1}{3}\)

*that would be our answer, however, the convention is to exclude the "1" in front of variables so we are left with:

x = \(\frac{1}{3}\)

Using balanced billing, the monthly payment is $278

Using balanced billing to determine their monthly payment, we simply need to divide their total annual payment by the total number of months in a year. This will result to dividing the entire annual bill by 12 to determine the monthly payment.

Given that the Ross family spent $3,336 for electricity last year, we can calculate their monthly payment as follows:

Monthly payment = Total cost / Number of months

Monthly payment = $3,336 / 12

Monthly payment  = $278

Therefore, the Ross family's monthly payment for balanced billing will be approximately $278.

Learn more on monthly payment here;

https://brainly.com/question/14666711

#SPJ1

Move the decimal point to the right 2 places:

Answer:

S = 2π(3^2) + 2π(3)(8.2) = 67.2π = 211 cm^3

Answer:

4189

Step-by-step explanation:

Given sequence is:

\(a_n=74n-29\)

Plugging n = 57 in the given sequence, we find:

\(a_{57}=74(57)-29\)

\(a_{57}=4218-29\)

\(\huge \red{a_{57}= \boxed{4189}}\)

Answer:

∠BCD= 23

AC⏜= 95

Step-by-step explanation:

Brainliest please

The measure of ∠BCD is 62 degree.

The measure of arc AC is 75 degree.

A circle's arc is referred to as a portion or section of its circumference. A chord of a circle is a straight line that might be created by joining the arc's two ends. A semicircular arc is one whose length is exactly half that of a circle.

We have to use the formula to find the angles

m <C = ( Far arc - Near arc ) / 2

So, m <C = (147 - 23) / 2

m <C = 124/ 2

m<C = 62

Again, m <B = (Arc AD - Arc AC) / 2

95 = (55x - 17x )/2

190 = 38x

x= 190/ 38

x = 5

So, the measure of arc AC is 17x = 17(5)= 75

Learn more about Arc here:

https://brainly.com/question/18741430

#SPJ7

Answer:

70 gold and bronze

Step-by-step explanation:

Add gold at 20 percent and bronze at 50 percent to get 70 percent gold and bronze.

After answering the presented question, we can conclude that expressions Therefore, the population of the rural city in 2030 is approximately 11,014.18.

In mathematics, you can multiply, divide, add, or subtract. An expression is constructed as follows: Number, expression, and mathematical operator A mathematical expression is made up of numbers, variables, and functions (such as addition, subtraction, multiplication or division etc.) It is possible to contrast expressions and phrases. An expression or algebraic expression is any mathematical statement that has variables, integers, and an arithmetic operation between them. For example, the expression 4m + 5 has the terms 4m and 5, as well as the provided expression's variable m, all separated by the arithmetic sign +.

To approximate the population in 2030, we need to find the value of P(t) when t = 44, since 2030 is 44 years after 1986.

Using the given exponential growth model, we have:

\(P(t) = 3400^(0.0371t)\\P(44) = 3400^(0.0371*44)\\P(44) = 3400^1.6334\\P(44) = 11014.18\\\)

Therefore, the population of the rural city in 2030 is approximately 11,014.18.

To know more about expressions visit :-

https://brainly.com/question/14083225

#SPJ1

Answer:

To make it easier to display the answer, the answers are in the picture attached below!

I'm doing good this morning!

13125

Step-by-step explanation:

The formula for kinetic energy is 1/2 times mass times velocity squared

in this situation the formual is 1/2 × 42 × 25 squared

42 divided by two is 21 so the new problem is

21 × 25 squared which is also

21 × 25 × 25= 13125 joules

The Distance between the points (4, -2) and (7, -9) is sqrt(58) or approximately 7.62 units.

The distance between two points in a coordinate plane. The distance formula is based on the Pythagorean theorem and calculates the straight-line distance between two points.

The coordinates of the first point as (x1, y1) = (4, -2) and the coordinates of the second point as (x2, y2) = (7, -9).

The distance formula is given by:

d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

Plugging in the values:

d = sqrt((7 - 4)^2 + (-9 - (-2))^2)

d = sqrt((3)^2 + (-7)^2)

d = sqrt(9 + 49)

d = sqrt(58)

Hence, the distance between the points (4, -2) and (7, -9) is sqrt(58) or approximately 7.62 units.

To know more about Distance .

https://brainly.com/question/23848540

#SPJ11

Answer:

D all the real numbers greater than or equal to -3

Step-by-step explanation:

The value of x is 24 and different angles of hexagon will be -

A = 160

B = 142

C = 120

D = 156

E = 31

F = 111

An angle is a geometric shape that is defined as the amount of rotation that occurs between two straight lines or planes. Angles are measured in degrees, with 360° representing a full circle.

We need to apply the inverse tangent function to determine the angle at which the sun strikes the flagpole. We are aware that the triangle's adjacent side is 42 feet long and its opposite side is 25 feet tall (the height of the flagpole) (the length of the shadow).

Given the figure is hexagon,

the sum of angles of a hexagon is 720,

Upon adding the given angles,

mA = (7x-8)°

mB (4x+46)°

mC = (5x)

mD = (6x+12)°

mE = (x+7)°

mF = (5x-9)°

⇒ 7x - 8 + 4x + 46 + 5x + 6x + 12 + x + 7 + 5x - 9 = 720

⇒ 28x + 48 = 720

⇒ 28x = 672

⇒ x = 24

Therefore, the angles will be -

A = 160

B = 142

C = 120

D = 156

E = 31

F = 111

To know more about angle click-

https://brainly.com/question/28769265

#SPJ1