Question 1: Factor −6x^2 + 18x.
Question 2: Rewrite 6x + 36 using a common factor.
Answers
\( \phi = - 6x {}^{2} + 18x \\ \phi = - 6x(x - 3)\)
Question 2:\( \psi = 6x + 36 \\ \psi = 6(x + 6)\)
Answer:
Step-by-step explanation:
Answer:
Question 1 = -6x(x-3)
Question 2 = 6(x+6)
Step-by-step explanation:
Hope this helps
Related Questions
How to do this problem

Answers
Answer:
a. geometric series
b. r_n = 100 × (0.75)^n ft
c. 400
Step-by-step explanation:
a.
Start: 100 ft
After 1 hour: 75% of 100ft = 100 ft × 0.75
After 2 hours: 75% of 100ft × 0.75 = 100 ft × 0.75²
After 3 hours: 75% of 100 ft × 0.75² = 100 ft × 0.75³
Notice what is happening to the radius as the hours pass.
With each passing hour, the radius is 0.75 times the previous radius.
Since each new term is the previous term multiplied by a constant, 0.75, this is a geometric series.
b.
At each hour, multiply 100 ft by 0.75 raised to the number of the hour.
a_n = 100 × (0.75)^n ft
The nth term is 100 times 0.75 to the nth power.
c.
The sum of all the radii is the sum of a series that has 100 as its first term, and each subsequent term is 0.75 times the previous term.
r_n = 100(0.75)^n
Since the constant ratio has an absolute value less than 1, the series has a sum.
S = a_1/(1 - r)
S = sum of infinite series
a_1 = first term
r = constant ratio
S = 100/(1 - 0.75)
S = 100/0.25
S = 400
The average monthly income of three persons is rs. 3,600. If the income of the first is 1/5 of the combined income of the other two then his monthly income is
Answers
The monthly income of the first person is $600.
Given that, the average monthly income of three persons is RS 3,600.
The income of the first is 1/5 of the combined income of the other two.
Here, Let income of the first be A, let income of the second be B and let Income of the third be C.
A+B+C=3600 -----(i)
Income for the first person = 1/5(B+C) -----(ii)
Substitute equation (ii) in equation (i), we get
(B+C)/5 +B+C =3600
B+C+5B+5C=3600×5
6B+6C=18000
6(B+C)=18000
B+C=3000 ------(iii)
Substitute (iii) in equation (i), we get
A=$600
Therefore, the monthly income of the first person is $600.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ1
solve for x to the nearest tenth
I WILL MARK BRAINLIEST.
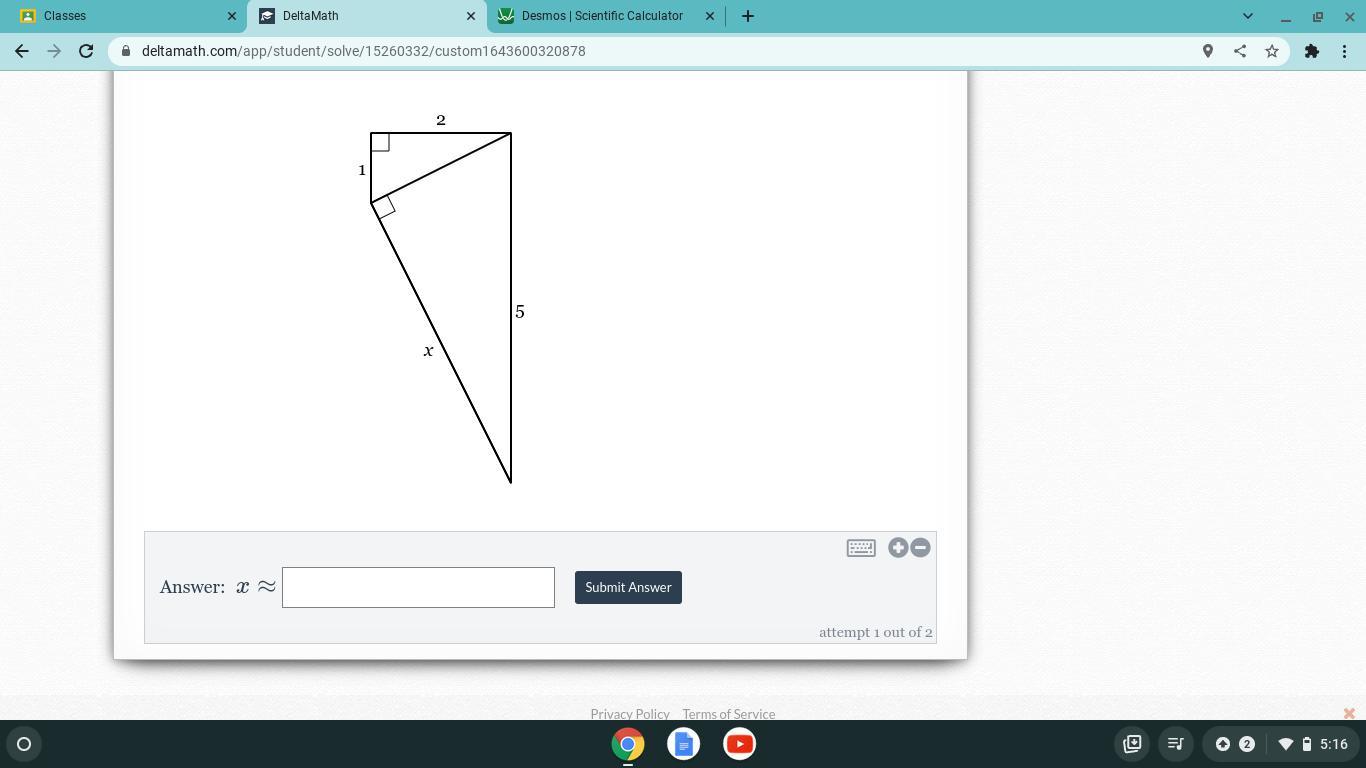
Answers
Look at the pictures.
can somebody help me

Answers
Answer:
-2 , 0 , 2
Step-by-step explanation:
HOPE THIS HELPS
PLZZ MARK BRAINLIEST
Answer:
the box after 4 is 2, 0, -2
Step-by-step explanation:
-2,0,2,4,6,8
It's counting down by two's
Someone please help me with this ASAP

Answers
Answer:
B. Fixed fee for Company B is greater than Company A
Step-by-step explanation:
Company A:
A(n) = $0.99 + $0.25n
The function above is given in slope-intercept form, A(n) = mx + b (rewritten as A(n) = b + mx)
The unit rate (m) = per minute fee = $0.25
Fixed fee (b) = $0.99)
Company B: let's find the fixed fee (b), which is the y-intercept.
The y-intercept is the point on the y-axis where the line intercepts the y-axis.
If we draw a straight line, we would observe that the y-intercept (b) would be between 1.20 and 1.40.
Therefore, fixed fee for Company B would be between $1.2 and $1.4. this is greater than the fixed fee for Company A, which is $0.99.
Therefore, the statement that must be true is:
B. Fixed fee for Company B is greater than Company A
Please answer this!!
(Can’t get option b)

Answers
1. The two vectors parallel to the plane: Vector AB = (8, -5, 4) and Vector AC = (0, 7, 6)
2. The vector perpendicular to the plane is (-58, -48, 56).
How do we calculate for vectors parallel and perpendicular to the plane?
To find the vectors parallel to the plane, we begin by finding the vectors AB and AC.
Vector AB = B - A = (11 - 3, -5 - 0, 2 - (-2)) = (8, -5, 4)
Vector AC = C - A = (3 - 3, 7 - 0, 4 - (-2)) = (0, 7, 6)
To find a vector perpendicular to the plane, we can take the cross product of the two vectors we found in part (a), AB and AC.
AB × AC = (AB_y * AC_z - AB_z * AC_y, AB_z * AC_x - AB_x * AC_z, AB_x * AC_y - AB_y * AC_x)
If we insert the figures, it will be
= ((-5) x 6 - 4 x 7, 4 x 0 - 8 x 6, 8 x 7 - (-5) x 0)
= (-30 - 28, -48, 56)
= (-58, -48, 56)
Consider the plane determined by the points A(3, 0, -2), B(11, -5, 2) and C(3, 7, 4).
a. Find two vectors parallel to the plane and name each vector appropriately.
b. Find a vector perpendicular to the plane.
Find more exercises on finding vectors parallel and perpendicular to a plane;
https://brainly.com/question/30591437
#SPJ1
9. A has some amount of money with him. He gave one half of one third from that amount One half of the amount received by B is 20. What is the amount that A originally had?
Answers
Using the expression 5x/12 = 20, the amount that A originally had was $48.
We have,
Let x be the amount of money that A originally had.
Then, A gave away 1/2 x 1/3 = 1/6 of the amount, which is equal to x/6.
The amount received by B is 1/2 of the remaining amount,
which is (x - x/6)/2 = 5x/12.
We know that 5x/12 = 20,
Solving for x.
5x/12 = 20
5x = 240
x = 48
Therefore,
The amount that A originally had was $48.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
How many solutions does 9x+7=8x+7
Answers
Answer:
One
Step-by-step explanation:
The equation 9x+7=8x+7 has only one solution. This can be seen by setting the two sides of the equation equal to each other and then solving for x.
First, we set the two sides equal to each other by canceling out the 7 on the right side of the equation:
9x+7 = 8x+7
Then, we move all of the terms that have an x on the same side of the equation, and all of the constant terms on the other side:
9x - 8x = 7 - 7
Next, we combine like terms on the left side of the equation:
x = 0
Finally, we solve for x to find the value of x that makes the equation true:
x = 0
Therefore, the only solution to the equation 9x+7=8x+7 is x=0.
For any positive integer n, the value of n! is the product of the first n positive integers. For example, 4! = 4 * 3 * 2 * 1 =24. What is the greatest common divisor of 5! and 7! ?
Answers
The GCD of 5! and 7! is 2^3 * 3^1 * 5^1 = 120.
the greatest common divisor of 5! and 7! is 120.
To find the greatest common divisor (GCD) of 5! and 7!, we need to factorize both numbers and identify the common factors.
First, let's calculate the values of 5! and 7!:
5! = 5 * 4 * 3 * 2 * 1 = 120
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5,040
Now, let's factorize both numbers:
Factorizing 120:
120 = 2^3 * 3 * 5
Factorizing 5,040:
5,040 = 2^4 * 3^2 * 5 * 7
To find the GCD, we need to consider the common factors raised to the lowest power. In this case, the common factors are 2, 3, and 5. The lowest power for 2 is 3 (from 120), the lowest power for 3 is 1 (from 120), and the lowest power for 5 is 1 (from both numbers).
For more such question on greatest common divisor
https://brainly.com/question/219464
#SPJ8
If 9x - 3y = -10 and 3x - 4y = 1 are true equations, what would be the value
of 12x-7y?
Answers
Answer:
Step-by-step explanation:
9x-3y=-10 ...............(1)
3x-4y=1...............(2)
multiplying equation (2) by 3
9x-12y=3...................(3)
Using elimination method, then
9x-3y=-10 ...............(1)
9x-12y=3...................(3
9y= -13
y= -13/9
substituting y= -13/9 in equation (1) then
9x-3(-13/9)= -10
9x+13/3= -10
multiplying throughout by 3
27x+13= -30
27x= -30-13
27x= -43
x= -43/27
since x and y values are known, then
12x-7y = 12(-43/27) - 7(-13/9)
12x-7y = -516/27 + 91/9
12x-7y = -9
An inch is exactly 2.54
centimeters.
Write an equation to convert the number of inches x
to the corresponding length in centimeters.
Enter the equation in the box.
Answers
Answer:
x * 2.54 = centimeters
Step-by-step explanation:
The equation to convert inches to centimeters is as follows:
x inches * 2.54 cm/inch = y centimeters
Where x is the number of inches and y is the equivalent length in centimeters.
To elaborate, the conversion factor between inches and centimeters is 2.54 cm/inch, meaning that for every inch there are 2.54 centimeters. To convert from inches to centimeters, we simply multiply the number of inches by the conversion factor. This gives us the equivalent length in centimeters.
question is the picture
it’s triangles congruent please help me if ur a nice person

Answers
Answer: The answer is the first choice, <L = <P
Step-by-step explanation:
There are two triangles.
Triangle LMN
and
Triangle PQR
If both of these triangles are congruent then that must mean that:
<L = <P
<M = <Q
<N - <R
Hope this helps!!
A warehouse placed 10 equal weight bones on a scale. Total they weighed 6 pounds. Each
box weighed
of a pound
Answers
A 4-sided polygon is classified as a quadrilateral.
True
False
Answers
Answer:
TRUEEEEEEEEEEEEEEEEEE
Step-by-step explanation:
 Hey guys, I would really appreciate if one of you help me with this question

Answers
Answer: 28.25%
Step-by-step explanation:
113/400=0.2825=28.25%
10. Write an algebraic expression that represents the perimeter of the figure shown below.
Simplify completely. Show your work.
3x
X
8x
4x
10x
2x

Answers
The perimeter of the given figure is 56x.
What do we mean by perimeter?A closed path that encompasses, encircles, or outlines a one-dimensional length or a two-dimensional shape is called a perimeter. A circle's or an ellipse's circumference is referred to as its perimeter. There are numerous uses in real life for perimeter calculations.So, perimeter: sum of all the sides
Then, according to the given figure:
Algebraic expression: 3x + x + 8x + 4x + 10x + 2x + (10x + 8x + 3x) + (x + 4x + 2x)28x + (10x + 8x + 3x) + (x + 4x + 2x)28x + 21x + 7x49x + 7x56xTherefore, the perimeter of the given figure is 56x.
Know more about perimeter here:
https://brainly.com/question/19819849
#SPJ9
The sector of a circle has an area of 104pi/9 square inches and a central angle with measure 65 degrees. What is the radious of the circle in inches? Show work. a. 5.7 b. 8 c. 64 d. 104
Answers
Answer: b. 8
Step-by-step explanation: I don’t have work
The radius of the circle in inches should be considered as the 8 when the measurement of the central angle is given.
Calculation of the radius of the circle;Since
The sector of a circle has an area of 104pi/9 square inches and a central angle with measure 65 degrees.
Also we know that
Area of the sector = \(65 / 360 *\) Area of circle
\(104\pi \div 9 = 65\div 360 (\pi r^2)\\\\104\div 9 = 65\div 360 r^2\\\\\)
r = 8
Hence, The radius of the circle in inches should be considered as the 8.
Learn more about circle here: https://brainly.com/question/15593101
I need help solving this

Answers
The cylinder has a volume of 150.796 in³. The cylinder has a surface area of 175.929 in².
What's volume of cylinder ?The quantity of three-dimensional space that an object or closed surface occupies is referred to as volume in mathematics. The cubic units of volume are m³, cm³, in³, and so on.
How does surface area work?The sum of all of an object's faces is its surface area in three dimensions. Wrapping, painting, and finally building things to achieve the best possible design are examples of real-world applications of the concept of surface areas.
Evaluating :Given that a volume of cylinder = h × r² × π
h = 12 in
r = 2 in
volume = ?
Volume of cylinder = h × r² ×π
= =12 × 3.14×(2)²
=37.68 × 4
=150.796 in³
B). Surface area of cylinder= 2πr² + 2πrh
=2× 3.14 × (2)²+2× 3.14× 2×12
=175.929in²
The formula V=r²(h) can be used to determine a cylinder's volume. Simply multiplying the area of the circular base shape by the height is all that is required to determine a cylinder's volume.
Learn more about Volume of cylinder :
brainly.com/question/24055431
#SPJ1
JKLM is a rhombus.
m/JMN = (-x+69)*
mZLMJ = (-6x +166)
K
N
M
Find the mZLKN.
label optional

Answers
The angle LKN in the rhombus is 62 degrees.
How to find angles in a rhombus?A rhombus is a quadrilateral that has 4 sides equal to each other. The sum of angles in a rhombus is 360 degrees.
Opposite angles are equal in a rhombus. The diagonals bisect each other at 90 degrees. Adjacent angles add up to 180 degrees.
Therefore, let's find ∠LKN as follows:
m∠JMN = (-x + 69)
m∠LMJ = (-6x + 166)
Therefore,
1 / 2 (-6x + 166) = -x + 69
-3x + 83 = -x + 69
-3x + x = 69 - 83
-2x = -14
x = -14 / -2
x = 7
Therefore,
∠LKN = 1 / 2 (-6x + 166)
∠LKN = 1 / 2 (-6(7) + 166)
∠LKN = 1 / 2 (-42 + 166)
∠LKN = 62 degrees
learn more on rhombus here: https://brainly.com/question/30995617
#SPJ1
3(g-8)=18 solve for g
Answers
Step-by-step explanation:
1.: Distribute the 3: 3g-24=18
2.: Add 24 to both sides: 3g=42
3.: Divide by 3: 3g/3=42/3
4.: Answer: g=14
Answer:g=14
Step-by-step explanation:
3(g-8)=18
3g-24=18
3g-24+24=18+24
3g=42
\(\frac{3g}{3} =\frac{42}{3}\)
g = 14
Annalise earns $4 an hour walking pets in her neighborhood. She evaluates the expression 4h, where h represents the number of hours, to find the amount she earns. Can any number be substituted for h? Explain.
Answers
Hope this helps:)
Are these triangles congruent? If so, name the triangle congruence method.

Answers
Answer:
The answer you chose is correct
Step-by-step explanation:
4. Attractiveness and a Great Sense of Humor (Based on Exercise 9.21, part a) In the Preview for Chapter 9 of the textbook, the authors discussed a study by McGee and Shevlin (2009) demonstrating that an individual’s sense of humor had a significant effect on how the individual was perceived by others. In one part of the study, female college students were given brief descriptions of a potential romantic partner. The fictitious male was described positively and, for one group of participants, the description also said that he had a great sense of humor. After reading the description, each participant was asked to rate the attractiveness of the man on a seven-point scale from 1 (very unattractive) to 7 (very attractive) with a score of 4 indicating a neutral rating.
a. Write the null and alternative hypotheses to determine if the females who read the “great sense of humor” description gave the potential partner an average attractiveness rating that was higher than neutral (μ = 4).
Answers
Null Hypothesis: The average attractiveness rating given by females who read the "great sense of humor" description is not higher than neutral,
μ ≤ 4
Alternative Hypothesis: The average attractiveness rating given by females who read the "great sense of humor" description is higher than neutral, μ > 4.
We have,
The null and alternative hypotheses to determine if the females who read the "great sense of humor" description gave the potential partner an average attractiveness rating that was higher than neutral (μ = 4) can be written as:
Null Hypothesis: The average attractiveness rating given by females who read the "great sense of humor" description is not higher than neutral,
μ ≤ 4
Alternative Hypothesis: The average attractiveness rating given by females who read the "great sense of humor" description is higher than neutral, μ > 4.
Thus,
The null hypothesis states that the mean attractiveness rating of males who are described positively and with a great sense of humor is not significantly different from a neutral rating of 4.
The alternative hypothesis states that the mean attractiveness rating of such males is significantly higher than a neutral rating of 4.
Learn more about hypothesis testing here:
https://brainly.com/question/30588452
#SPJ1
Choose the definition for the function PLS HELP
Answers
Answer:
Which function please explain
An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
In Steven's grade, 12 students are enrolled in health and 48 students are not. What percentage of the students in the school are enrolled in health?
Answers
Answer:
20%
step-by-step way
plz help me with this

Answers
Answer:
11 shots
Step-by-step explanation:
60% of 18 = 10.8
10.8 rounded = 11
Why we did this:
Owen made 60% of the shots he made, and he made 18 shots in total. Therefore, we would take 60% of 18.
The answer we get is 10.8, but we can't have a part of a shot. That wouldn't make sense. Therefore, we have to round up to 11 shots.
Select the correct answer.
What is the value of x in the triangle?
a 30-60-90 triangle with long leg length x and shorter leg length of 7 times the square root of 3
Answers
The length of the hypotenuse is 7m.
Let the side opposite to 30° be the shortest leg.
The side opposite to 60° is the longest leg.
So, the side opposite to 90° is hypotenuse.
Length of the shortest side is x.
Length of longest side is \(\sqrt{3}x\)
Length of the hypotenuse is 2x.
We know x = 7
So, \(\sqrt{3}(x)=\sqrt{3}(7)\)
Thus, the length of the longer leg is \(\sqrt{3}(7)\) m
Length of hypotenuse = 2x = 2(7) = 14m
\(x^{2} +(\sqrt{3} x)^2 =(2x)^2\\\\(7)^2+(\sqrt{3} (7))^2=(2x)^2\\\\49 + (3(49)) = (2x)^2\\\\49 + 147= (2x)^2\\\\(2x)^2=196\)
Taking square root on both sides:
\(2x = \sqrt{196}\)
2x = 14
x = 7
Therefore, the length of the hypotenuse is 7m.
Learn more about Triangle at:
https://brainly.com/question/2773823
#SPJ1
6. Mini muffins cost $3.00 per dozen. • Andre says, “I have $2.00, so I can afford 8 muffins.” • Elena says, “I want to get 16 muffins, so I’ll need to pay $4.00.” Do you agree with either of them? Explain your reasoning.
Answers
Answer: I agree with both of them
Step-by-step explanation:
A dozen is 12
And a dozen cost $3.00,
To get how many mini muffins they can get for$1.00= 12/3 =4 mini muffins
Andre has $2.00 =2*4=8 he can get 8 mini muffins.
Elena wants 16 mini muffins.
She'll need $4.00
=16/4= $4.00
Three spherical balls with radius r are contained in a rectangular box. two of the balls are each touching 5 sides of the rectangular box and the middle ball. the middle ball also touches four sides of the rectangular box. What is the volume of the space between the balls and the rectangular box? This is a SAT question and is no calculator. Show all the work Answer is 4r^3(6-pi)
Answers
Answer:
The volume of the space between the balls and the rectangular box is \(4r^{3}(6 - \pi)\)
Step-by-step explanation:
The attachment below shows the description of the rectangular bow and the three spherical balls.
From the description,
Two of the balls are each touching 5 sides of the rectangular box, say the 5 sides touched by one of the balls are sides 1,2,3,4, and 5; then the other ball will touch sides 2,3,4,5, and 6). The middle ball also touches four sides of the rectangular box, These four sides touched by the middle ball will be sides 2,3,4, and 5.This means the balls are tightly fitted into the rectangular box.
Each of the balls has a radius r
Hence, The volume of one of the balls is given by the volume of a sphere
\(Volume of a sphere = \frac{4}{3} \pi r^{3} \\\)
The volume occupied by one of the balls is \(\frac{4}{3} \pi r^{3} \\\)
∴ The volume occupied by the three spherical balls will be
3 × \(\frac{4}{3} \pi r^{3} \\\)
= \(4\pi r^{3}\)
The volume occupied by the three spherical balls \(4\pi r^{3}\)
For the rectangular box,
The volume of a rectangular box = \(l w h\)
Where \(l\\\) is the length
\(w\) is the width and
\(h\) is the height
Since the balls are tightly packed,
The width of the rectangular box will be the diameter of the balls
diameter of the balls = 2r
∴ \(w\) = 2r
The height of the rectangular box will also be the diameter of the balls
∴ \(h\) = 2r
The length of the rectangular box will be 3 times the diameter of the balls
∴\(l\) = 3 × 2r = 6r
Hence,
The volume of a rectangular box = 6r × 2r × 2r
= 24r³
The volume of the space between the balls and the rectangular box is given by
Volume of the space between the balls and the rectangular box =
volume of the rectangular box - volume occupied by the three spherical balls
Volume of the space between the balls and the rectangular box= 24r³ - 4πr³
= 24r³ - 4πr³
= 4r³(6 - π)
