Question 1-7
Similar triangles MRC and WYC are shown where MR = 14, CR=28, WY = 6, and MW = 17.88.
What is the length of YC?

Answers
In the triangle WYC, the length of the side YC is 4.76 units.
What is a triangle?A triangle is a three-sided closed-plane figure formed by joining three noncolinear points. Based on the side property triangles are of three types they are Equilateral triangle, Scalene triangle, and Isosceles triangle.
We know a line segment parallel to a side of a triangle divides the other two sides in the same ratio.
Given, In a ΔMRC and ΔWYC MR = 14, CR=28, WY = 6, and MW = 17.88.
Now, MR = 14 and MW = 17.88.
Therefore, (MW/MR) = 17.88/14 = 1.28.
So, If WY = 6, then WE = (1.28)(6) = 7.66.
Now, In the ΔWYC, WY = 6 and WE = 7.66.
Therefore from the Pythagoras's theorem,
WE² - WY² = YC².
YC² = (7.66)² - 6².
YC² = 22.68.
YC = 4.76.
learn more about triangles here :
https://brainly.com/question/2773823
#SPJ1
Related Questions
2- (-4)= what is the answere
Answers
Answer:
The answer is 6.
Step-by-step explanation:
A negative and a negative makes a positive when the problem is written as
x - (-x)
So 2 - (-4) equals 2 + 4
which is simply 6
Answer:
6
Step-by-step explanation:
Two negatives cancel out a positive.
2-(4) should turn into 2 +4
2+4 =6
What is the value of the fallowing when x = 0
A. y = -5
B. y = -2
C. y = -1
D. y = 0

Answers
Answer:
B
Step-by-step explanation:
When x = 0 we are looking at the y- axis
The graph crosses the y- axis at y = - 2
Thus when x = 0 then y = - 2 → B
Find the 100th term in the number pattern described by "Start at 13 and add 2 each time."
A) 15
B) 211
C)213
D)215
HELP PLEASE.
Answers
Answer:
213
Step-by-step explanation:
the equations for this is y=2x+13
just plug in x to find y
y=2(100)+13
y=213
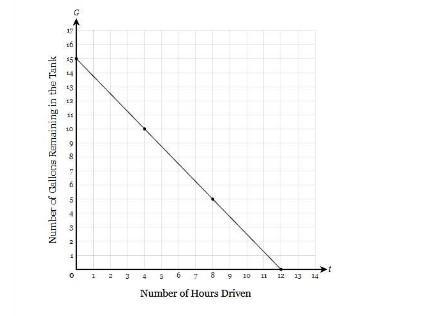
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
What is 50% of 50% of 50%
Answers
Step 1:
50%= 50/100 = 0.5
Step 2:
50% of 50%= (50×0.5)/100= 0.25
Step 3:
50% of 50% of 50% = (50×0.25)/100= 0.125
Thanks for joining brainly community!
How do you find the original price if the percent of discount is 25% in the sales price is $40
Answers
25% — $40
100% — $40 * 4 = $160
The original price is $160.
For a test concerning a mean, a sample of size n =90 is obtained. In testing H0: u<=u0 versus H1: u>u0, the test statistic is 1.91. Find the p-value (round off to third decimal place).
Answers
The p-value for the given test is approximately 0.028, rounded off to the third decimal place.
To find the p-value for a test concerning a mean, where the sample size is n = 90 and the test statistic is 1.91, we need to determine the probability of observing a test statistic as extreme as or more extreme than the one obtained under the null hypothesis.
Since the alternative hypothesis is u > u0, we are conducting a right-tailed test.
The p-value is the probability of observing a test statistic greater than or equal to the observed test statistic under the null hypothesis.
To calculate the p-value, we can use the cumulative distribution function (CDF) of the appropriate distribution, which in this case is the t-distribution.
Since the sample size is large (n = 90), we can approximate the t-distribution with a standard normal distribution.
Using a standard normal distribution, we can find the p-value as follows:
p-value = 1 - CDF(t), where t is the observed test statistic.
p-value = 1 - CDF(1.91)
Calculating this using a standard normal distribution table or a statistical software, we find that the p-value is approximately 0.028.
Therefore, the p-value for the given test is approximately 0.028, rounded off to the third decimal place.
Learn more about p-value here:
https://brainly.com/question/32087607
#SPJ11
hi i’m gonna need some help on this i don’t understand at all

Answers
Let's begin by finding the mean of the data
\(\begin{gathered} \text{Mean = }\frac{\sum x}{n}=\text{ }\frac{46\text{ + 47 + }5\text{6 + 48 + }46\text{ + 52 + }5\text{7 + 52 + 4}5}{9} \\ \text{Mean = }\frac{449}{9}=48.89\text{ }\approx\text{ 48.9} \end{gathered}\)Mean = 48.9
Next, we calculate the absolute value of the difference between each data value and the mean, we have:
|data value – mean|
|46 - 48.9| = 2.9
|47 - 48.9| = 1.9
|56 - 48.9| = 7.1
|48 - 48.9| = 0.9
|46 - 48.9| = 2.9
|52 - 48.9| = 3.1
|57 - 48.9| = 8.1
|52 - 48.9| = 3.1
|45 - 48.9| = 3.9
Next, we sum up the absolute values of the differences (from above) & divide by the number of data values, we have:
\(\begin{gathered} MOD=\frac{2.9\text{ + 1.9 + 7.1 + 0.9 + 2.9 + 3.1 + 8.1 + 3.1 + 3.9}}{9}=\frac{69}{9} \\ \text{MOD = 7.7 }\approx\text{ 8 (to the nearest whole number)} \end{gathered}\)MOD = 8 (to the nearest whole number)
A right triangle has legs measuring 5 feet and 12 feet. If the legs of the triangle were doubled, what would be the difference in the original and enlarged perimeters?
Answers
Answer:
\(30\)
Step-by-step explanation:
1. Approach
First, use the Pythagorean theorem to solve for the hypotenuse of the given right triangle. Then find the perimeter by adding up the values of all the sides. The problem then has the lengths of the legs doubled. When the legs undergo a scaling factor, the hypotenuse and perimeter undergo the same scaling factor. Here, the legs are doubled, hence the hypotenuse and the perimeter are also doubled. Finally, subtract the new perimeter from the original perimeter.
2. Find the original hypotenuse
Remember the Pythagorean theorem states;
\(x^{2}+y^{2}=z^{2}\)
Where (a) and (y) are the legs (or the sides adjacent to the right angle), and (z) is the hypotenuse or the side opposite to the right angle.
Substitute in the given value and solve,
\((5)^{2}+(12)^{2}=z^{2}\\\\25 + 144 = z^{2}\\\\169=z^{2}\\\\\sqrt{169}=z\\\\13=z\)
3.Find the perimeter of the original triangle
To find the perimeter of a polygon, one must add up the lengths of all the sides.
\(5 + 12 + 13\\\\= 30\)
4. Find the new perimeter
In a right triangle, when both legs undergo a scaling factor, the hypotenuse also has the same change, and the perimeter also undergoes the same change. In this case, the length of the legs is doubled, therefore, the hypotenuse and the perimeter are also doubled.
New hypotenuse; \(26\)
New perimeter; \(60\)
5. Find the difference
Now all that is left is to subtract the new perimeter from the original perimeter;
(New_perimeter) - (original_perimeter)
= \(60 - 30\)
= \(30\)
a 3.5-oz box of candy has a total of 21.0 g of fat. how many grams of fat would a 14-oz box of candy contain?
Answers
The amount of fat contained in the 14-oz box of candy is 84 grams.
Define the term ratios of the number?A ratio in mathematics is a contrast of two or more values that shows how big one is in comparison to the other. The dividend as well as number being divided is referred to as the antecedent, and the divisor as well as number that's also dividing is referred to as the consequent. A ratio compares two numbers by division. Regardless matter why a ratio is expressed, it is crucial to reduce it to the fewest whole numbers, just like with any fraction. To accomplish this, divide the integers by their largest common factor after discovering it.Total fat in 3.5-oz box of candy = 21.0 g.
Let x be the fat contained in the 14-oz box of candy.
Then, taking the ratios.
3.5 / 21 = 14 / x
x = 14 × 21 / 3.5
x = 84 grams
Thus, the amount of fat contained in the 14-oz box of candy is 84 grams.
To know more about the ratios of the number, here
https://brainly.com/question/12024093
#SPJ4
Is the following relation a function? Yes or no

Answers
Answer:
It is a many-to-many function but not a one-to-ine function hence, it cannot be represented a a function in an expression
Step-by-step explanation:
Topic: Functions
If you would like to venture further into mathematics, you can check out my Instagram page (learntionary) where I post notes and mathematics tips. Thanks!
Answer: No
Explanation: I think that the least confusing way to do
this problem is to first write down the ordered pairs that
are represented by this mapping diagram.
So we have {(6,3), (-1, 2), (-1, -1), (4, 3)}.
In order for a relation to be a function, each x-coordinate needs
to appear once unless we have a repeated ordered pair.
Since we have the same x-coordinate in two of
our ordered pairs, this relation cannot be a function.
In terms of the mapping diagram, you can see that we have
an x that is paired with two different y's.
So this does not fit the definition of a function which states
that each x must be paired with exactly one y.
pleaseee help :15x+32=200
Answers
Answer:
11.2
Step-by-step explanation:
15x + 32 = 200 Subtract 32 from both sides
15x + 32 - 32 = 200 - 32
15x = 168 Divide both sides by 15
\(\frac{15x}{15}\) = \(\frac{168}{15}\)
x = 11.2
Answer:
i think the answer is x= 11.2
Step-by-step explanation:
15x= 200-32
15x=168
x=168/15
x=11.2
use a number line to find the product.
5 x (-5)
a. -25
b. 25
c. 10
d. 0
Answers
Answer: a. -25
Step-by-step explanation:
1. Multiply the numbers
5x(−5)
Solution
−25x
State whether the following statement is true or false. The Law of Sines can be used to solve triangles where three sides are known Choose the correct answer below. A. False, because to use the Law of Sines, all three angles must be known B. True, because to use the Law of Sines, all three sides must be known. C. True, because to use the Law of Sines, at least two sides must be known D. False, because to use the Law of Sines, two angles and one side or two sides and one angle must be known.
Answers
C. True, because to use the Law of Sines, at least two sides must be known.
The Law of Sines is a trigonometric rule that relates the sides and angles of any triangle. It states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides of the triangle.
To use the Law of Sines, at least two sides and the angle opposite one of them (or two angles and one side) must be known.
Therefore, the statement "The Law of Sines can be used to solve triangles where three sides are known" is false, as it is not necessary to use the Law of Sines to solve a triangle where all three sides are known.
In summary, the correct answer is C. True, because to use the Law of Sines, at least two sides must be known.
To know more about Law of Sines:
https://brainly.com/question/28827357
#SPJ11
A soccer team scores 12 points in 5 matches. They scored the same number of points in each of their first 3 matches and one more point in each of their last 2. How many points did they score in each match?
Answers
Answer:
2 points the first 3 matches then 3 points the last 2 matches
Step-by-step explanation:
12 points in 5 matches and the first 3 are all the same then the other 2 increased by 1 point
They got 2 points the first 3 matches then 3 points the last 2 matches
2 + 2 + 2 (first 3 matches) = 6
3 + 3 (last 2 matches) = 6
6 + 6 = 12
if currently there are four cars occupying four of the six spots in a random arrangement, what is the probability that you will have to parallel park?
Answers
The probability of a parallel park in the 5th spot out of 6 random arrangements is 2 ÷ 5.
The probability of the need to parallel park equal to the probability of 2 open spaces in the first 5 spots and not together equals the number of 2 possible open spots in the first 5 and not together ÷ The number of 2 possible open spots = (The number of 2 possible open spots in the first 5 - The number of 2 possible open spots together in the first 5) ÷ The number of 2 possible open spots.
The number of 2 possible open spots in the first 5 = nCr = C(5,2) = 10
The number of 2 possible open spots together in the first 5 = 4
The number of 2 possible open spots = nCr = C(6,2) = 15
The probability of the need to parallel park = (10 - 4) ÷ 15
= 6 ÷ 15
= 2 ÷ 5
To learn more about probability at
https://brainly.com/question/11234923?referrer=searchResults
#SPJ4
Points A, B, and C are collinear. Point B is between A and C. Find the length of of segment AC if the measure of segment AB= 8 and the measure of segment BC = 6. Just provide the value of the length
Answers
Answer:
The value of the length of AC is 14
Step-by-step explanation:
When points are collinear, it simply means that the points lie on the same straight line.
In this question , we have three points which lie on same straight line.
These are points A, B and C with B between A and C.
Thus the length AC can be obtained by adding the length of AB to the length of BC
Mathematically, the value of the length of AC will be 8 + 6 = 14
Amount
Expense
Mortgage
Gasoline
$650
$150
$130
Groceries
Car Insurance
590
Clothes
$80
About what percent of Davon's monthly budget was spent on groceries?
F
12%
13%
H
896
J
1.18%
Answers
Answer:oline
$650
$150
$130
Groceries
Car Insurance
590
Clothes
$80oline
$650
$150
$130
Groceries
Car Insurance
590
Clothes
$80
About what percent of Davon's monthly budget w
About what percent of Davon's monthly budget w
Step-by-step explanation:
oline
$650
$150
$130
Groceries
Car Insurance
590
Clothes
$80
About what percent of Davon's monthly budget w
Answer:
the one i got is 12%
Step-by-step explanation:
but im not sure if its correct
compute the flux of the vector field f through the surface s. f = −xz i − yz j z2k and s is the cone z = x2 y2 for 0 ≤ z ≤ 9, oriented upward. f · da s =
Answers
The first integral becomes ∫∫\(R u^5 v^4 (2uv^2) \sqrt{(4u^2v^2 + 1) du}\)
To compute the flux of the vector field F through the surface S, we can use the surface integral formula:
flux = ∬s F · dA
where dA is the differential area element of the surface S and the double integral is taken over the entire surface.
In this case, the vector field F is given by:
F = −xz i − yz j + \(z^2 k\)
And the surface S is the cone \(z = x^2 y^2\)for 0 ≤ z ≤ 9, oriented upward. To find the differential area element dA, we can use the parametrization of the surface in terms of u and v:
x = u
y = v
\(z = u^2 v^2\)
where (u, v) ranges over the region R = {(u, v) | 0 ≤ u ≤ 3, 0 ≤ v ≤ 3}.
The partial derivatives of the parametrization are:
∂x/∂u = 1, ∂x/∂v = 0
∂y/∂u = 0, ∂y/∂v = 1
∂z/∂u = \(2uv^2, ∂z/∂v = 2u^2v\)
Using these, we can find the cross product of the partial derivatives:
∂r/∂u x ∂r/∂v = \((-2uv^2) i + (2u^2v) j + k\)
and the magnitude of this vector is:
|∂r/∂u x ∂r/∂v| = \(\sqrt{((2uv^2)^2 + (2u^2v)^2 + 1) } = \sqrt{(4u^2v^2 + 1)}\)
Therefore, the differential area element is:
dA = |∂r/∂u x ∂r/∂v| du dv = sqrt(4u^2v^2 + 1) du dv
Now we can compute the flux of F through S using the surface integral formula:
flux = ∬s F · dA
= ∫∫R F(u, v) · (∂r/∂u x ∂r/∂v) du dv
Substituting in the expressions for F and the cross product, we have:
flux = ∫∫\(R (-uxz -vyz + z^2) (-2uv^2 i + 2u^2v j + k) \sqrt{(4u^2v^2 + 1) du dv}\)
The limits of integration are u = 0 to u = 3 and v = 0 to v = 3. We can break this up into three separate integrals:
flux = ∫∫\(R (-uxz) (-2uv^2) \sqrt{ (4u^2v^2 + 1) du dv}\)
+ ∫∫\(R (-vyz) (2u^2v) \sqrt{(4u^2v^2 + 1) du dv}\)
+ ∫∫\(R z^2 \sqrt{(4u^2v^2 + 1) du dv}\)
The first integral can be simplified using the equation for the cone z = \(x^2 y^2:\)
\(uxz = u(-u^2 v^2)(u^2 v^2) = -u^5 v^4\)
for such more question on integral
https://brainly.com/question/22008756
#SPJ11
Consider the diagram below of an equilatera triangle.

Answers
Answer:
4 = n.
13 ft.
Step-by-step explanation:
An equilateral triangle means that all of the sides are equal.
This means: 2n + 5 = 3n + 1 = 5n -7
You can pick two of those sides to set up an equation to solve for n.
For example, 2n + 5 = 3n + 1.
Then you will need to isolate the variable.
Subtract 1 from each side to get 2n + 4 = 3n.
Subtract 2n from each side to get 4 = n.
Substitue 4 for n into one of the equations.
2n + 5
2(4) + 5
8 + 5 = 13
Each side is 13 ft.
for f(x)=8x+8, find f(x) when x=5
A:-32
B:56
C:104
D:48
Answers
Answer:
D. 48
Step-by-step explanation:
f(x)=8x+8
f(x)=40+8
f(x)=48
Mai wants to have at least $200 to take with her on vacation to buy souvenirs she currently has $80 saved and is going to earn the rest by babysitting she will make $8 an hour babysitting write an inequality that represents the number of hours she will need to babysit
Answers
A rectangular vegetable patch has a perimeter of 40 meters. Its area is 64 square meters. What are the dimensions of the vegetable patch?
Answers
The dimensions of the vegetable patch are 8 meters by 12 meters or 12 meters by 8 meters.
Let's assume the length of the vegetable patch is L and the width is W.
Given, the perimeter of the rectangular vegetable patch = 40 meters.
Perimeter = 2(L+W) = 40
Simplifying the above equation, we get
L+W = 20 (Equation 1)
Also, given that the area of the vegetable patch = 64 square meters.
Area = L*W = 64
From Equation 1, we can write W = 20-L
Substituting W in terms of L in the area equation, we get
L*(20-L) = 64
Expanding the above equation, we get
-L^2 + 20L - 64 = 0
Solving the quadratic equation, we get two possible values for L.
L = 8 or L = 12
If L = 8, then W = 20 - L = 12
If L = 12, then W = 20 - L = 8
Therefore, the dimensions of the vegetable patch are 8 meters by 12 meters or 12 meters by 8 meters.
Learn more about vegetable patch,
https://brainly.com/question/16606311
#SPJ4
Which is the slope of the line that passes through the points (2,8) and (4,6)?
Answers
Answer:
The slope would be -2/2 or when simplified, -1.
Answer:
-1
Step-by-step explanation:
Isla has 225 trading cards and Lily has 180 trading cards. a) Calculate the number of Isla's trading cards as a percentage of the number of Lily's trading cards. b) Calculate the number of Lily's trading cards as a percentage of the number of Isla's trading cards. Give your answers to the nearest 1%.
Answers
(a) Isla's trading cards are 125% of Lily's trading cards.
(b) Lily's trading cards are 80% of Isla's trading cards.
Given that,
There are 225 trading cards and Lily has 180 trading cards.
To calculate the percentage of Isla's trading cards compared to Lily's,
We can use this formula:
⇒ Isla's trading cards / Lily's trading cards x 100%
Plugging in the values we get:
⇒ (225 / 180) x 100% = 125%
Therefore,
Isla's trading cards are 125% of Lily's trading cards.
b) To calculate the percentage of Lily's trading cards compared to Isla's, we can use the formula:
⇒ Lily's trading cards / Isla's trading cards x 100%
Plugging in the values we get:
(180 / 225) x 100% = 80%
Therefore,
Lily's trading cards are 80% of Isla's trading cards.
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ1
Someone plz help me

Answers
Answer:
16 is the answer hope i helped!
Step-by-step explanation:
Answer:
i think it c
:D
Step-by-step explanation:
A jar contains 4 green marbles 2 pink marbles 3 striped marbles. One marble is picked at random and then replaced. Then another marble is drawn at random again. What is the probability that both marbles are striped?
Answers
Answer:
25%
Step-by-step explanation:
Answer: It’s 1/9 I got the same question on my test.
1. Find the exact values of each of the six trigonometric functions of an angle θ, if (-3,3) is a point on its terminal side. 2. Given that tan θ = and sin θ <0, find the exact value of each of the remaining five trigonometric functions of θ.
Answers
Finding the six trigonometric functions of θ: Since (-3,3) is a point on the terminal side of θ, we can use the coordinates of this point to determine the values of the trigonometric functions.
Let's label the legs of the right triangle formed as opposite = 3 and adjacent = -3, and use the Pythagorean theorem to find the hypotenuse.
Using Pythagorean theorem: hypotenuse² = opposite² + adjacent²
hypotenuse² = 3² + (-3)²
hypotenuse² = 9 + 9
hypotenuse² = 18
hypotenuse = √18 = 3√2
Now we can calculate the trigonometric functions:
sin θ = opposite/hypotenuse = 3/3√2 = √2/2
cos θ = adjacent/hypotenuse = -3/3√2 = -√2/2
tan θ = opposite/adjacent = 3/-3 = -1
csc θ = 1/sin θ = 2/√2 = √2
sec θ = 1/cos θ = -2/√2 = -√2
cot θ = 1/tan θ = -1/1 = -1
Therefore, the exact values of the six trigonometric functions of θ are:
sin θ = √2/2, cos θ = -√2/2, tan θ = -1, csc θ = √2, sec θ = -√2, cot θ = -1.
Part 2: Finding the remaining trigonometric functions given tan θ and sin θ:
Given that tan θ = and sin θ < 0, we can deduce that θ lies in the third quadrant of the unit circle where both the tangent and sine are negative. In this quadrant, the cosine is positive, while the cosecant, secant, and cotangent can be determined by taking the reciprocals of the corresponding functions in the first quadrant.
Since tan θ = opposite/adjacent = sin θ/cos θ, we have:
sin θ = -1 and cos θ =
Using the Pythagorean identity sin² θ + cos² θ = 1, we can find cos θ:
(-1)² + cos² θ = 1
1 + cos² θ = 1
cos² θ = 0
cos θ = 0
Now we can calculate the remaining trigonometric functions:
csc θ = 1/sin θ = 1/-1 = -1
sec θ = 1/cos θ = 1/0 = undefined
cot θ = 1/tan θ = 1/-1 = -1
Therefore, the exact values of the remaining five trigonometric functions of θ are:
sin θ = -1, cos θ = 0, tan θ = -1, csc θ = -1, sec θ = undefined, cot θ = -1.
To learn more about Pythagorean theorem click here:
brainly.com/question/14930619
#SPJ11
slope-intercept form, write the equation of the line
that passes through the point (4, 2) with a slope of 5.
Answers
Answer:
\(y=5x-18\)
Step-by-step explanation:
Given the following question:
Point A = (4, 2) = (x, y)
Slope = 5
To find the answer we are going to have to use the formula for slope intercept, substitute the values, then solve for the variable b to have our answer.
\(y=mx+b\)
\(y=2\)
\(m=5\)
\(x=4\)
\(2=5(4)+b\)
\(5\times4=20\)
\(2=20+b\)
\(20-20=0\)
\(2-20=-18\)
\(-18=b\)
\(b=-18\)
\(y=5x-18\)
Your answer is "y = 5x - 18."
Hope this helps.
Initially, there were only 86 weeds in the garden. The weeds grew at a rate of 8% each week. The following function represents the weekly weed growth: f(x) = 86(1.08)x. Rewrite the function to show how quickly the weeds grow each day.
Answers
Answer:
f(x) = 86(1.01)^7x; They grow at approximately the rate of 1% per day.
Step-by-step explanation
86 is the number of weeds at the starting point of the question.
8/7% each day, 7 being the total number of days in the week, the weekly growth 8%: 1 day is 8/7% growth or 1.14% rounded up to 1%
In the original equation the 8% growth was represented by 1.08
Substituting the weekly rate of 8% with the daily rate of 1%, or 1.08 with 1.01 the new function is:
f(x) = 86(1.01)^7x