Proportions: Aubrey's car used 2 gallons to travel 90 miles. How far can she travel on 11 gallons?
Answers
Answer:
495 gallons
Step-by-step explanation:
2= 90
11=?
90×11÷2
= 495 gallons
Related Questions
4-31. You are gambling on a chess tournament with three matches taking place: 4 Probability and Counting 4.5 Exercises All players are equally matched, so the probability of any player winning a match is 1/2. You must guess which player will win each match. It costs you $10 to play, with prizes as follows: - Your original $10 back, plus an additional $20 if you guess all three matches correctly. - Your original $10 back if you guess exactly two of the matches correctly. - An amount of $2 if you guess a single match correctly. (a) Let X be the value of your winnings, so that X=0 corresponds to breaking even, a negative value of X corresponds to losing money, and a positive value of X means you win money. What is the expected value of X ? (b) You bribe Tyler to deliberately lose his match, guaranteeing that Parker will win. Assuming you pick Parker to win, what is the expected value of your winnings now?
Answers
a) The expected value of your winnings is $3.75.
b) The expected value of your winnings is $5.625.
(a) To calculate the expected value of X, we need to find the probability of each outcome and multiply it by the corresponding value of winnings.
Let's consider the possible outcomes:
Guessing all three matches correctly: Probability = \((1/2)^{3}\)= 1/8. Winnings = $10 + $20 = $30.
Guessing exactly two matches correctly: Probability = 3 * \((1/2)^{3}\) = 3/8. Winnings = $10.
Guessing exactly one match correctly: Probability = 3 * \((1/2)^{3}\) = 3/8. Winnings = $2.
Guessing none of the matches correctly: Probability = \((1/2)^{3}\) = 1/8. Winnings = -$10.
Now, we can calculate the expected value using the formula:
Expected Value (E[X]) = Sum of (Probability * Winnings) for all outcomes.
E[X] = (1/8) * $30 + (3/8) * $10 + (3/8) * $2 + (1/8) * (-$10)
= $3.75
Therefore, the expected value of your winnings is $3.75.
(b) If you bribe Tyler to deliberately lose his match, the probability of Parker winning becomes 1. Now, there are only two possible outcomes:
Guessing all three matches correctly (Parker wins all): Probability = 1/8. Winnings = $10 + $20 = $30.
Guessing exactly two matches correctly (Parker wins two): Probability = 3/8. Winnings = $10.
Now, we can calculate the expected value:
E[X] = (1/8) * $30 + (3/8) * $10
= $5.625
Therefore, the expected value of your winnings, after bribing Tyler, is $5.625.
To learn more about expected value here:
https://brainly.com/question/13749480
#SPJ4
use the definition to find an expression for the area under the graph of f as a limit. do not evaluate the limit. f ( x ) = x 2 √ 1 2 x , 2 ≤ x ≤ 4
Answers
The expression for the area under the graph of f(x) over the interval [2, 4] is given by the limit as n approaches infinity of the Riemann sum: A = lim(n→∞) Σ[f(xi)Δx].
To express the area under the graph of f(x) as a limit, we divide the interval [2, 4] into n subintervals of equal width Δx = (4 - 2)/n = 2/n.
Let xi be the right endpoint of each subinterval, with i ranging from 1 to n. The area of each rectangle is given by f(xi)Δx.
By summing the areas of all the rectangles, we obtain the Riemann sum: A = Σ[f(xi)Δx], where the summation is taken from i = 1 to n.
To find the expression for the area under the graph of f(x) as a limit, we let n approach infinity, making the width of the rectangles infinitely small.
This leads to the definite integral: A = ∫[2, 4] f(x) dx.
In this case, the expression for the area under the graph of f(x) over the interval [2, 4] is given by the limit as n approaches infinity of the Riemann sum: A = lim(n→∞) Σ[f(xi)Δx].
Evaluating this limit would yield the actual value of the area under the curve.
Learn more about Riemann sum here:
https://brainly.com/question/30404402
#SPJ11
Find the perimeter and area of the figure.

Answers
Answer:
perimeter of the figure =32 units
area of the figure=56 units²

What's the value of
\( \sqrt{25 \times 1} \)
Answers
Answer:
5
Step-by-step explanation:
\(\sqrt{25*1}= \sqrt{25}\)
\(\sqrt{25}=5\)
Square root of 25 is 5, because 5x5=25.
If f(x)=ln(x+4+e^(-3x)), then f '(0) =
Answers
If derivative of \(f(x)=ln(x+4+e^{(-3x)})\), then f '(0) = -2/5.
What is derivative?
In calculus, the derivative of a function is a measure of how the function changes as its input changes. More specifically, the derivative of a function at a certain point is the instantaneous rate of change of the function at that point.
To find f'(0), we first need to find the derivative of f(x) with respect to x. Using the chain rule, we get:
\(f'(x) = 1 / (x+4+e^{(-3x)}) * (1 - 3e^{(-3x)})\)
Now we can find f'(0) by substituting the value x=0:
\(f'(0) = 1 / (0+4+e^{(-3(0))}) * (1 - 3e^{(-3(0))})\)
f'(0) = 1 / (4+1) * (1 - 3)
f'(0) = -2/5
Therefore, f'(0) = -2/5.
To learn more about derivative visit:
https://brainly.com/question/23819325
#SPJ4
Suppose a consumer's utility function is given by: \[ U=x^{1 / 5} y^{4 / 5} \] This is an example of a Cobb-Douglas model. The Cobb-Douglas model is used extensively in economics. a) Set y=1 and graph the marginal utility of x; put marginal utility on the vertical axis and x on the horizontal axis. Your graph does not have to be perfect, but it should have the correct shape. b) What is the MRS for this consumer? Explain in words what the MRS is.
Answers
a) To graph the marginal utility of x, we need to find the derivative of the utility function with respect to x. Given that y=1, the utility function becomes U=x^(1/5). Taking the derivative of U with respect to x, we get dU/dx = (1/5)x^(-4/5). This represents the marginal utility of x.
When we graph the marginal utility of x, we put the marginal utility on the vertical axis and x on the horizontal axis. Since x^(-4/5) is positive for all positive values of x, the graph of the marginal utility of x will have a positive slope that decreases as x increases. The shape of the graph will resemble a downward-sloping curve that approaches zero as x approaches infinity.
b) The MRS (Marginal Rate of Substitution) for this consumer is the rate at which the consumer is willing to trade one good for another while keeping the total utility constant. In this case, the MRS is the negative ratio of the marginal utility of x to the marginal utility of y. Mathematically, MRS = -(dU/dx)/(dU/dy).
Since y is a constant and dU/dy = 0, the MRS simplifies to MRS = -(dU/dx)/0 = undefined. This means that the consumer is not willing to trade any amount of y for x, as the marginal utility of y is zero. The consumer only derives utility from x and does not value y in terms of marginal utility.
The graph of the marginal utility of x will have a positive slope that decreases as x increases. The MRS for this consumer is undefined, indicating that the consumer does not value y in terms of marginal utility.
To know more about marginal utility , visit ;
https://brainly.com/question/34280910
#SPJ11
the differnce of a number x and 30 is 10
Answers
I think X = 40
As a member of a dance troupe, Anita has a costume wardrobe that consists of 2 pairs of tights (1 white pair and 1 black pair), 3 T-shirts (1 pink, 1 blue, and 1 green), and 3 scarves (1 silver, 1 gold, and 1 white). If a costume consists of either a pair of tights and a T-shirt with a scarf or a pair of tights and a T-shirt without a scarf, how many different costumes are possible?
Answers
Answer:
24
Step-by-step explanation:
24
The total number of different costumes possible is 24 if Anita has a costume wardrobe that consists of 2 pairs of tights, 3 T-shirts, and 3 scarves.
What are permutation and combination?A permutation is the number of different ways a set can be organized; order matters in permutations, but not in combinations.
We have:
Anita has a costume wardrobe that consists of 2 pairs of tights (1 white pair and 1 black pair), 3 T-shirts (1 pink, 1 blue, and 1 green), and 3 scarves (1 silver, 1 gold, and 1 white).
The costume consists of either a pair of tights or a T-shirt with a scarf:
In this case total number of ways = 2×3×3 = 18
Pair of tights and a T-shirt without a scarf:
In this case total number of ways = 2×3 = 6
Total number of different costumes are possible:
= 18 + 6
= 24
Thus, the total number of different costumes possible is 24 if Anita has a costume wardrobe that consists of 2 pairs of tights, 3 T-shirts, and 3 scarves.
Learn more about permutation and combination here:
https://brainly.com/question/2295036
#SPJ2
Betsy has a bag with three mint sticks eight jelly treats and nine fruit tart chews if she eats one piece every three minutes what is the probability her first two pieces will be a fruit tart chew and a jelly treat
Answers
If Betsy has a bag with three mint sticks, eight jelly treats, and nine fruit tart chews and she eats one piece every three minutes, the probability her first two pieces will be a fruit tart chew and a jelly treat is 18.9%.
The probability of her first two pieces being a fruit tart chew and a jelly treat can be calculated as follows,
First, we divide the expected outcomes by the total possible outcomes.
Total possible outcomes = 3(mint sticks) + 8(jelly treats) + 9(fruit tart chews) = 20
Hence,
Probability for fruit tart chew: 9 ÷ 20
Probability for jelly treat: 8 ÷ 19 (as one possibility is considered to be fruit tart chew)
The probability of her first two pieces to be fruit tart chew and jelly treat can be determined by multiplying the probability for fruit tart chew with the probability for jelly treat,
Probability = (9/20)(8/19)
Probability = 72/380 = 0.189
Converting into percentage,
Probability = 0.189 × 100 = 18.9%
Hence, the probability that her first two pieces will be a fruit tart chew and a jelly treat is equal to 18.9%.
To learn more about probability, click here:
https://brainly.com/question/251701
#SPJ4
umm please help me it is confusing
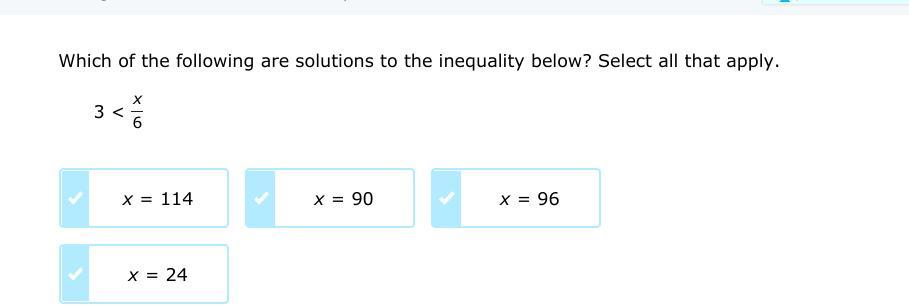
Answers
Answer: x = 24 & x = 96
Step-by-step explanation:
Answer: Every option given is a solution
Any value larger than 18 is a solution. So we can say x > 18.
============================================================
Explanation:
To isolate x, we multiply both sides by 6 like so
3 < x/6
3*6 < x
18 < x
x > 18
In the last step, I swapped the left and right sides. This swap meant that I had to flip the inequality sign as well. Saying x > 18 means we can pick anything larger than 18 to have it as a solution. Something like x = 5 is too small, but values like x = 24 and x = 96 will work. In fact, all of the answer choices given are larger than 18. So you'll check each answer box.
---------
As a way to confirm a potential answer, we plug it back into the original inequality. Let's say we wanted to check x = 90
So,
3 < x/6
3 < 90/6 ... replace every x with 90
3 < 15
The last inequality is true, because 3 is indeed smaller than 15. Therefore, the original inequality is true when x = 90. We confirm that x = 90 is a solution.
The steps to confirm x = 114, x = 96, and x = 24 will follow the same idea. I'll let you do those confirmations.
The measures of the exterior angles of a quadrilateral are 3x°,8x°, 9x°, and 10x°. Find the measure of the largest exterior angle.
Answers
The measure of the largest exterior angle of the quadrilateral is 120 degrees
QuadrilateralsQuadrilateral are polygons that have four sides. They are regarded as a four sided polygon.
Therefore, the measures of the exterior angles are as follows;
3x°8x°9x°10x°The sum of all the exterior angles of a quadrilateral is 360°. Therefore,
3x + 8x + 9x + 10x = 360°
30x = 360
x = 360 / 30
x = 12
Therefore, the greatest/largest exterior angle is as follows;
10(12) = 120°learn more on quadrilateral here: https://brainly.com/question/26150522
Please help me fast
What is the equation of this graph

Answers
Answer-4,5
Step-by-step explanation:
The symbol x¯ represents the population mean of all possible sample means of size n.
False
True
Answers
False. The symbol x¯ represents the population mean of all possible sample means of size n.
The symbol x¯ (x-bar) represents the sample mean, not the population mean of all possible sample means of size n. The population mean of all possible sample means of size n is denoted by μ (mu). The sample mean, x¯, is calculated by taking the average of the observations in a specific sample.
Know more about population mean here;
https://brainly.com/question/30324262
#SPJ11
under what circumstances is the point-biserial correlation used?
Answers
Answer: when one of the variables is dichotomous; when you need to measure the relationship between a continuous variable and a dichotomous variable.
Step-by-step explanation:
What is 7/9 as a percent and decimal?
Answers
Answer:
7.78% (Approx of 7.77....) and
0.78 ( again approx of 0.7777..
Step-by-step explanation:
For Decimal simply do long division.
Multiplying the answer with 100 will give us percentage
Hope this helps!!
The ratio of boys to girls is 4 to 6. If the school has 800 students, how many are girls
Answers
Answer:
Yo, there would be 320 boys and 480 girls. Cheers
Step-by-step explanation:
Since the ratio is 4:6. that just means there's 1.5 the amount of girls as there is boys.
Answer:
480
Step-by-step explanation:
No
Can someone help me with this math homework please!

Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
\(h(10) \text{- the altitude of the hot air balloon after 10 minutes.}\\\\\boxed{h(10)=60}\)
»»————- ★ ————-««
Here’s why:
⸻⸻⸻⸻
As described in the question, the function \(h(t)\) models the total altitude of a hot air balloon over time. 't' represents the number of minutes that would be given.\(h(10)\) would be the total altitude over 10 minutes time. To solve for the value, we would replace 't' with 10 and then evaluate.⸻⸻⸻⸻
\(\boxed{\text{Evaluating the function...}}\\\\h(t) = 210 - 15t; \text{ } h(10)\\-------------\\\rightarrow h(10) = 210 - 15(10)\\\\\rightarrow h(10)=210 - 150\\\\\rightarrow \boxed{h(10) = 60}\)
⸻⸻⸻⸻
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
What is the forecast for May using a five-month moving average?(Round answer to the nearest whole number.) Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47
A. 43 B. 47 C. 52 D. 38 E. 39
Answers
The forecast for May using a five-month moving average is 39 (Option E).
Moving average is used for smoothing out time series data to find any trends or cycles within the data. A five-month moving average is the average of the past five months. To calculate the moving average, add up the sales for the previous five months and divide it by five.
According to the question, the sales for the previous five months are: Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47
We have to add the sales of these five months, which gives:
27 + 40 + 42 + 41 + 47 = 197
To find the moving average for May, we divide this sum by 5:
197 / 5 = 39.4
Since we have to round the answer to the nearest whole number, we round 39.4 to 39, which is option E.
Learn more about Moving average here: https://brainly.com/question/28495879
#SPJ11
The Alexander family and the Martin family each used their sprinklers last summer. The water output rate for the Alexander family's sprinkler was 25L per hour. The water output rate for the Martin family's sprinkler was 35L per hour. The families used their sprinklers for a combined total of 45 hours, resulting in a total water output of 1425L. How long was each sprinkler used
Answers
Both sprinklers with a water output rate of 25L per hour and 35L per hour were used for a combined total of 45 hours, resulting in a total water output of 1425L.
To determine the duration of each sprinkler's use, we can solve a system of equations.
Let's denote the duration of the Alexander family's sprinkler use as x hours and the duration of the Martin family's sprinkler use as y hours. Since the water output rate is the amount of water per hour, we can set up the following equations:
25x + 35y = 1425 (equation for total water output)
x + y = 45 (equation for total duration)
To solve this system of equations, we can use substitution or elimination. Let's use the elimination method. Multiply the second equation by 25 to eliminate x:
25x + 25y = 1125
Now subtract this equation from the first equation:
25x + 35y - (25x + 25y) = 1425 - 1125
10y = 300
Divide both sides by 10:
y = 30
Substituting this value back into the second equation, we find:
x + 30 = 45
x = 15
Therefore, the Alexander family's sprinkler was used for 15 hours, and the Martin family's sprinkler was used for 30 hours.
Learn more about elimination method here:
https://brainly.com/question/13877817
#SPJ11
which fraction is equivalent to 612? select each correct answer. responses 46 4 over 6 38 3 over 8 36 6 over 12 24 2 over 4 12 1 over 2 26
Answers
The fractions equivalent to 6/12 are 6/12, 2/4, and 1/2.
1. 4/6: To see if these fractions are equivalent, we can simplify 6/12. Divide both the numerator and the denominator by their greatest common divisor, which is 6. 6/12 ÷ (6/6) = 1/2. Now, simplify 4/6 by dividing both by their greatest common divisor, which is 2. 4/6 ÷ (2/2) = 2/3. These fractions are not equivalent, as 1/2 ≠ 2/3.
2. 3/8: This fraction cannot be equivalent to 6/12, as their denominators are different and don't have a common factor. So, no further calculation is needed.
3. 6/12: This fraction is the same as the original fraction and is therefore equivalent to itself.
4. 2/4: Simplify 2/4 by dividing both the numerator and the denominator by their greatest common divisor, which is 2. 2/4 ÷ (2/2) = 1/2. This fraction is equivalent to 6/12, as 1/2 = 1/2.
5. 1/2: As we found out earlier, 6/12 simplifies to 1/2, so this fraction is equivalent to 6/12.
Learn more about common divisor here:
brainly.com/question/29199768
#SPJ11
g(x) =
=
कर
4
+7
What is the average rate of change of g over the
interval [-2, 4]?
Answers
The average rate of change of g over the interval [-2, 4] is 4
What is the average rate of change of g over the interval [-2, 4]?The equation of the function is given as:
g(x) = 4x + 7
Calculate the value of the functions
g(-2) and g(4)
So, we have:
g(-2) = 4 * -2 + 7 = -1
g(4) = 4 * 4 + 7 = 23
The average rate of change of g over the interval [-2, 4] is then calculated as:
Rate = g(4) - g(-2)/4 - 2
This gives
Rate = (23 + 1)/(4 + 2)
Evaluate
Rate = 4
Hence, the average rate of change of g over the interval [-2, 4] is 4
Read more about average rate of change at
https://brainly.com/question/8728504
#SPJ1
Complete question
g(x) = 4x + 7
What is the average rate of change of g over the interval [-2, 4]?
g if k < n - r, the value of max value(r, 0, k) should be the larger of two expressions. one of these expressions has -1 as the second parameter to maxvalue. what is it?
Answers
The larger of the two expressions is maxvalue(r, n - k - r, k).
The expression with -1 as the second parameter to maxvalue is maxvalue(n-k-r, -1, k).
To see why this is the case, let's consider the definition of maxvalue(r, a, b). This function returns the maximum value among r, a, and b.
Now, suppose that k < n - r. Then, we have:
n - k - r > n - (n - r) - r = r
This means that n - k - r is greater than r, so maxvalue(r, n - k - r, k) will return either n - k - r or k, whichever is greater.
On the other hand, since -1 is less than any non-negative integer, we have:
-1 < 0 <= r
Therefore, maxvalue(r, -1, k) will return either r or k, whichever is greater.
Since r is non-negative, we have:
maxvalue(r, -1, k) = max(r, -1, k) = max(r, k)
So, the larger of the two expressions is maxvalue(r, n - k - r, k).
To learn more about expression visit:
https://brainly.com/question/14083225
#SPJ11
PLEASE HELP ASAP!!! THIS IS MY LAST QUESTION FOR THE DAY!! SHOW WORK PLEASE

Answers
Answer:
ΔHLN ≅ ΔHFCReason: ASABecause:
∠CHF ≅ ∠NHLHC ≅ HN∠HCF ≅ ∠HNLWhat is the area of this figure?

Answers
Answer:
I feel like a lot of people try to get people just to do the work for them on this site.
Step-by-step explanation:
To actually find the area of this shape without using a too high level of math, you would split the shapes into geometric shapes and you should find that you have all the values to make that line up. Just remember to be careful. This will take a moment which is why i'm not doing it. Remember area = b*h area of triangle = 1/2*b*h
Find the area enclosed by the curve x 3t, y t and the y-axis. Step 1 The curve x = t2-3t, y = Vt intersects the y-axis when x = 0, which occurs when t = 0 and 3 3 H 3 '
Answers
The area enclosed by the curve x = t^2 − 3t, y = √t and the y-axis is 2.08 square units.
We have been given parametric equations x = t^2 − 3t, y = √t
We need to find the area enclosed by the curve x = t^2 − 3t, y = √t and the y-axis.
Consider x = 0
So, t^2 − 3t = 0
t(t - 3) = 0
t = 0 or t = 3
Let f(t) = t^2 − 3t and g(t) = t
Differentiate the curve f(t) with respect to t.
f'(t) = 2t - 3
NWe know that the formula to find the area under the curve.
A = ∫[a to b] g(t)f'(t) dt
here, a = 0 and b = 3
so, A = ∫[0 to 3] √t (2t - 3) dt
A = ∫[0 to 3] (2t√t - 3√t) dt
A = ∫[0 to 3] (2t^(3/2) - 3t^(1/2)) dt
A = [4/5 t^(5/2) - 2 t^(3/2)]_[t = 0, t = 3]
A = 4/5 3^(5/2) - 2 3^(3/2) - 0 + 0
A = 4/5 3^(5/2) - 2 3^(3/2)
A = 6√3 /5
A = 2.08
Therefore, the area of the curve is 2.08 square units.
Learn more about parametric equations here:
brainly.com/question/28537985
#SPJ4
The area of a rectangle is 105 sq in and the length of one side is 7 in. What is the length of the perimeter?
Answers
Perimeter of Rectangle is 44m
What is Perimeter ?A perimeter is a closed path that encompasses, encircles, or delineates a one-dimensional length or a two-dimensional shape.
According to the given information
Area of Rectangle = l × b
Area of Rectangle = 105 \(m^{2}\)
Length of one side = 7 m
Let the length of the adjacent side = b
Area of Rectangle given = 7 × b
105 = 7 × b
b = \(\frac{105}{7}\)
b = 15 m
Perimeter of Rectangle given = 2( l + b )
= 2 ( 7 + 15 )
= 2 × 22
= 44m
Perimeter of Rectangle is 44m
To know more about Perimeter
https://brainly.com/question/15271274
#SPJ4
Find the missing value. Hint: Use the number line to find the missing value. -7= -(-2)
Answers
Answer:
-9
Step-by-step explanation: I know this problem since I use khan academy too and I got the answer wrong and it helped by saying it was -9.
Simplify. Your answer should contain only positive exponents −ab^2•(2a^0b^-4)^-4•2a^4b^-1
Answers
Answer:
-a^5b^17/8
Step-by-step explanation:
-5x - 4y = -12
Convert from standard form slope intercept form
Answers
Answer:
y = -5/4x + 3
Step-by-step explanation:
slope-intercept form is: y = mx + b
where 'm' represents slope and 'b' represents the y-intercept
basically we have to solve for 'y':
first step, add -5x to each side to get:
-4y = 5x - 12
last step, divide each side by -4 to get:
y = -5/4x + 3
slope equals -5/4
y-intercept equals 3
At a construction site, the brace used to retain a wall is 9.6 m in length. The distance from the wall to the lower end of the brace (on the ground) is 5.3 m. Calculate the angle at which the brace meets the wall.
Answers
The angle at which the brace meets the wall is approximately 56.51 degrees.
To calculate the angle at which the brace meets the wall at a construction site, we can use the right triangle trigonometry. Here, the brace is the hypotenuse of a right-angled triangle, with the distance from the wall to the lower end of the brace being one of the legs. We will use these terms: construction, brace, and angle in our explanation.
Step 1: Identify the given measurements
- Length of the brace (hypotenuse) = 9.6 m
- Distance from the wall to the lower end of the brace (adjacent leg) = 5.3 m
Step 2: Use the cosine function to find the angle
cos(angle) = adjacent leg / hypotenuse
cos(angle) = 5.3 m / 9.6 m
Step 3: Calculate the angle using the inverse cosine function
angle = cos^(-1)(5.3 m / 9.6 m)
Step 4: Find the angle using a calculator
angle ≈ cos^(-1)(0.5521) ≈ 56.51°
So, at the construction site, the angle at which the brace meets the wall is approximately 56.51 degrees.
inverse cosine functionhttps://brainly.com/question/31149456
#SPJ11