Answers
Answer:
15
Step-by-step explanation:
Since, triangle ABC is the enlargement of triangle XYZ.
\( \therefore \triangle ABC \sim \triangle XYZ\)
So, corresponding sides of both the triangles would be in proportion.
\( \therefore \frac{x}{6}=\frac{25}{10}\)
\( \therefore x= \frac{6\times 25}{10}\)
\( \therefore x =\frac{150}{10}\)
\( \therefore x = 15\)
Related Questions
Cells lining the gut need to take in glucose but at a certain time, the concentration of extracellular glucose is lower than the concentration already stored in cells. What process is needed here?
Simple diffusion
Active transport
Facilitated diffusion
Answers
Option B, In this situation, when the concentration of extracellular glucose is lower than the concentration currently present in cells, active transport is required.
Active transport, as opposed to simple diffusion or assisted diffusion, uses energy (in the form of ATP) to move molecules up or down a concentration gradient, from a region of low concentration to one of high concentration.
To transfer glucose molecules into the stomach lining cells in spite of the concentration gradient, active transport would be required. This procedure is crucial for preserving the body's glucose homeostasis and guaranteeing that cells have enough glucose for cellular energy generation.
Learn more about active transport at
https://brainly.com/question/29759743
#SPJ4
PLEASEE answerrrrrr

Answers
Three-fourths of students in your classroom like chocolate chip cookie dough ice cream. One-half of these same students also like mint-flavored ice cream. What fraction of students in your classroom like both flavors?
ANSWER FOR 100 POINTS
Answers
The fraction of the students in the classroom that like both flavors is 1/4.
How to calculate the fraction?From the information, three-fourths of students in the classroom like chocolate chip cookie dough ice cream and one-half of these same students also like mint-flavored ice cream.
The fraction of the students in the classroom that like both flavors will be the addition of both flavors subtracted from 1. This will be illustrated as:
= (3/4 + 1/2) - 1
= 3/4 + 2/4 - 1
= 5/4 - 1
= 1/4
The fraction is 1/4.
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
what’s the area and perimeter

Answers
Answer:
The area= 1 in The perimeter= 5 in
Step-by-step explanation:
:)
I need help on this can you help me please
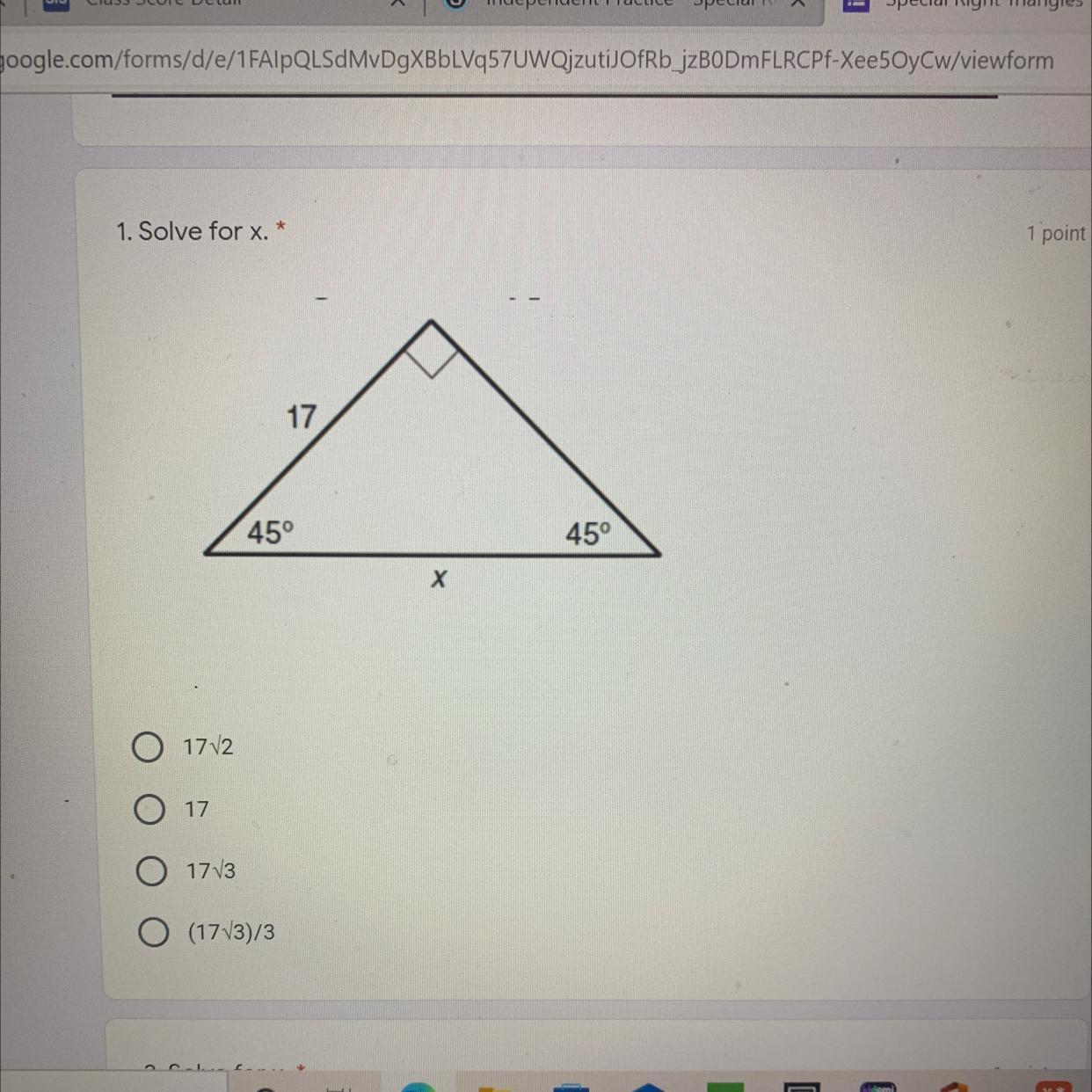
Answers
Since it is a right triangle, we can use the trigonometric ratio sin(θ).
\(\sin (\theta)=\frac{\text{ Opposite side}}{\text{Hypotenuse}}\)So, in this case, we have:
\(\begin{gathered} \theta=45\degree \\ \text{ Opposite side }=17 \\ \text{ Hypotenuse }=x \end{gathered}\)\(\begin{gathered} \sin (\theta)=\frac{\text{ Opposite side}}{\text{Hypotenuse}} \\ \sin (45\degree)=\frac{17}{x} \end{gathered}\)Now, we solve for x the above equation:
\(\begin{gathered} \text{Multiply by x from both sides} \\ \sin (45\degree)\cdot x=\frac{17}{x}\cdot x \\ x\sin (45\degree)=17 \\ \text{ Divide by }\sin (45\degree)\text{ from both sides} \\ \frac{x\sin(45\degree)}{\sin(45\degree)}=\frac{17}{\sin(45\degree)} \\ x=\frac{17}{\sin(45\degree)} \\ x=\frac{17}{\frac{1}{\sqrt[]{2}}} \\ x=\frac{\frac{17}{1}}{\frac{1}{\sqrt[]{2}}} \\ x=\frac{17\cdot\sqrt[]{2}}{1\cdot1} \\ x=\frac{17\sqrt[]{2}}{1} \\ $$\boldsymbol{x=17\sqrt[]{2}}$$ \end{gathered}\)Therefore, the value of x is:
\($$\boldsymbol{x=17\sqrt[]{2}}$$\)
One sheet of paper is 9 x 10 to the power of -3 to cm thick. Mark wants to put 500 sheets of paper into the paper tray of his printer. The paper tray is 4 cm deep. Is the paper tray deep enough for 500 sheets of paper? You must explain your answer. Input note: write down the thickness of the 500 sheets of paper.
Answers
Answer:
The paper tray is not deep enough.
Step-by-step explanation:
500 * 9 * 10^-3
= 500 * 0.009
= 4.5 cm which is greater than the depth of the paper tray (4 cm).
The paper tray is not enough for sheets of paper.
The thickness of 500 sheets of paper is 45 cm.
What is multiplication?Multiplication is an operation that represents the basic idea of repeated addition of the same number. The numbers that are multiplied are called the factors and the result that is obtained after the multiplication of two or more numbers is known as the product of those numbers.
One sheet of paper is \(9\) × \(10^{-3}\) to the power of -3 to cm thick.
Mark wants to put 500 sheets of paper into the paper tray of his printer.
The thickness of 500 sheets of paper is
\(9\) × \(10^{-3}\) × 500 = 45 cm
But the paper tray is 4cm deep
45 cm > 4 cm
So the paper tray is not enough for sheets of paper.
Find out more information about multiplication here
https://brainly.com/question/14059007
#SPJ2
In a right triangle, measure of one of the acute angles is 10 degrees more than 3 times the measure of the other angle. What are the measures of the three
angles?
Answers
Answer:
How do you find the angle of a right triangle with 3 sides?
Step-by-step explanation:
Step 1 The two sides we know are Adjacent (6,750) and Hypotenuse (8,100).
Step 2 SOHCAHTOA tells us we must use Cosine.
Step 3 Calculate Adjacent / Hypotenuse = 6,750/8,100 = 0.8333.
Step 4 Find the angle from your calculator using cos-1 of 0.8333:
Victor has saved $89.25 for the bicycle that he wants .the bicycle cost $129.85
Answers
The model used by Victor in the linear equation is incorrect,
How to identify Linear Equation Models?The parameters are that;
Victor saved: $89.25
Cost of the bicycle = $129.85
Thus, to find the amount extra that he will need to purchase the bicycle, the equation model should be;
$89.25 + x = $129.85
This can be expressed in words as;
The amount of money he already has saved + the amount of money he still requires = the total price of the bike.
An equation that correctly represents this problem can show the sum of the amount of money he already has and the amount of money he needs equals the total cost of the bicycle
Read more about linear Equation Model at; https://brainly.com/question/4074386
#SPJ1
Complete question is;
Victor has saved $89.25 for the bicycle that he wants. The bicycle costs $129.85. Victor writes the equation below to help him determine the additional amount that he needs to solve to have enough to buy the bicycle.
89.25 + 129.85 = x
Does Victor's equation correctly model the problem?
What is s = 5.1 inches
Answers
Answer:
16.02
Step-by-step explanation:
Lori had $126.89 in her bank account. She deposited $21.49 into it and then wrote a check for her car repairs for $156.61.
What was the ending balance in her account?
0-$51.21
$8.23
$8.23
O $51.21
Answers
Answer:
b
Step-by-step explanation:
on ed
Answer:
The answer is B!!
Step-by-step explanation:
suppose you want to line pennies up, diameter to diameter, until the total length is 1 kilometer. assume the width of 1 penny is 2 cm. how many pennies will you need? how accurate is this estimation?
Answers
Answer: 50,000 pennies
Step-by-step explanation: there are 100,000 centimeters in a kilometer, since a penny is 2 centimeters in length, divide 100,000 by 2 t get 50,000
On Venus, a cylindrical container that is 12 hhigh with a diameter of 4ft is 65% filed with an unknown liquid that has a weight of 160 bf. The fluid in the cylinder is under one atmosphere of pressure whiee in storage. Please give the followin answers. Do not put units in the answer entry box. Pay attontion to the units requested for each answer. Container Volume =
Answers
The volume of the cylindrical container on Venus can be calculated based on the given information.
To find the volume of the cylindrical container, we can use the formula for the volume of a cylinder: V = πr^2h, where V represents volume, r is the radius of the base, and h is the height of the cylinder. In this case, the diameter of the container is given as 4 feet, which means the radius (r) is half of that, or 2 feet. The height (h) of the container is given as 12 feet.
Using these values, we can calculate the volume as follows: V = π(2^2)(12) = 48π cubic feet.
However, we need to consider that the container is filled with an unknown liquid, and its weight is given as 160 pounds. The weight of the liquid is directly proportional to its volume, assuming the density remains constant. Since the fluid is 65% filled, we can calculate the total volume of the fluid by dividing the weight by the density and then multiplying by the percentage filled. However, without knowing the density of the liquid, we cannot determine the volume accurately. Therefore, the answer for the container volume is 48π cubic feet, assuming the density of the liquid remains constant throughout.
Learn more about cylindrical here:
https://brainly.com/question/25562559
#SPJ11
Determine the nature of the roots: 2x2 + 8x + 3 = 0
Answers
Answer:
the nature of the roots of an equation is real, distinct and irrational
Step-by-step explanation:
Given Data provided in the question according to the question is as follows:
\(2x^2 + 8x + 3 = 0\)
where
a = 2 , b = 8 , c = 3
As we know that
Quadratic expression
\(ax^2 + bx +c = 0\)
Delta = \(b^2 - 4ac\)
\(= (8)^2 - 4 (2) (3)\)
= 64 - 24
= 40
Here,
Delta > 0, it does not contain perfect square
Therefore the nature of the roots of an equation is real, distinct and irrational
GIVE BRAINLIEST!!! PLS LOVE U

Answers
Answer:
n word
Step-by-step explanation:
Step-by-step explanation:
Since the two triangles are congruent this means that corresponding angles are congruent so
Angle X= Angle M
Angle Y equal Angle N
Angle Z equal Angle L.
That means that Angle M is 33 degrees.
Angle Y is 124 degrees.
We can find Angle Z by doing triangle interior theorem.
\(124 + 33 + x = 180\)
\(157 + x = 180\)
\(x = 23\)
So Angle Z equal 23.
Congruent triangles also have corresponding sides that are equal so that means
XY=MN
YZ=NL
XZ= ML
So that means XY=8
Find a basis for and the dimension of the solution space of the homogeneous system of linear equations.
3x1 + 3x2 + 15x3 + 11x4 = 0
x1 − 3x2 + x3 + x4 = 0
2x1 + 3x2 + 11x3 + 8x4 = 0
(a) a basis for the solution space
(b) the dimension of the solution space
Answers
(a) A basis for the solution space of the homogeneous system of linear equations is:
{(-3, 1, 0, 0), (-5, 0, -5, 1)}
(b) The dimension of the solution space is 2.
To find a basis for the solution space, we first write the augmented matrix of the system and row-reduce it to its echelon form or reduced row-echelon form.
Then, we identify the free variables (variables that can take any value) and express the dependent variables in terms of the free variables. The basis for the solution space consists of the vectors corresponding to the free variables.
In this case, after performing row operations, we obtain the reduced row-echelon form:
[1 0 -1 -1 0]
[0 1 3 2 0]
[0 0 0 0 0]
The first and second columns correspond to the free variables x3 and x4, respectively. Setting these variables to arbitrary values, we can express x1 and x2 in terms of x3 and x4 as follows: x1 = -x3 - x4 and x2 = -3x3 - 2x4. Therefore, a basis for the solution space is {(-3, 1, 0, 0), (-5, 0, -5, 1)}.
Since the basis has 2 vectors, the dimension of the solution space is 2.
For more such answers on Linear Equation
https://brainly.com/question/2030026
#SPJ8
#12-15) Given its 3 sides, classify the triangle as right, acute, or obtuse. You must
show work to verify your answer.
12) 5, 7, 9
13) 5, 10, 5√3
14) √13, 10, 12
15) 16, 30, 34
Answers
It should be noted that 5, 7, 9 forms an obtuse triangle.
Also, 5, 10, 5√3 forms an acute triangle.
How to explain the trianglea² + b² = c²
5² + 7² = 25 + 49 = 74
9² = 81
Since 74 < 81, we know that 5, 7, 9 forms an obtuse triangle.
Again, we apply the Pythagorean theorem.
5² + (5√3)² = 25 + 75 = 100
(2√13)² = 52
Since 100 > 52, we know that 5, 10, 5√3 forms an acute triangle.
Applying the Pythagorean theorem:
(√13)² + 10² = 13 + 100 = 113
12² = 144
Since 113 < 144, we know that √13, 10, 12 forms an obtuse triangle.
Applying the Pythagorean theorem:
16² + 30² = 256 + 900 = 1156
34² = 1156
Since 1156 = 1156, we know that 16, 30, 34 forms a right triangle.
Learn more about Triangle on
https://brainly.com/question/17335144
#SPJ4
Given: y= x3 + 3x2 - 45x + 24 = We have a maximum at what value of x?
Answers
To find the maximum value of the given function, we need to take the derivative of the function and set it equal to zero.
y = \(x^{3}\) + 3\(x^{2}\)- 45x + 24
y' = 3\(x^{2}\) + 6x - 45
Setting y' equal to zero:
3\(x^{2}\)+ 6x - 45 = 0
Using the quadratic formula, we get:
x = (-6 ± \(\sqrt{( 6^{2} - 4(3)(-45)}\) / (2(3))
x = (-6 ± 18) / 6
x = -3, 5
To determine which value of x gives the maximum value of the function, we need to evaluate the second derivative of the function at each critical point.
y'' = 6x + 6
When x = -3:
y'' = 6(-3) + 6 = -12
When x = 5:
y'' = 6(5) + 6 = 36
Since the second derivative at x = 5 is positive, we know that x = 5 gives the maximum value of the function. Therefore, the maximum value of the function is:
y(5) = \(5^{3}\) + 3(\(5^{2}\)) - 45(5) + 24
y(5) = 124
Learn more about derivative here:
https://brainly.com/question/25324584
#SPJ11
The maximum value of y is 100, and it occurs when x = -4.
The maximum value for the given function y = x^3 + 3x^2 - 45x + 24. To find the maximum, we'll need to find the critical points of the function by taking the derivative and setting it equal to zero.
1. Find the derivative of the function with respect to x: y' = 3x^2 + 6x - 45
2. Set the derivative equal to zero and solve for x: 3x^2 + 6x - 45 = 0
3. Factor the quadratic equation: x = (-6 ± sqrt(6^2 - 4(3)(-45))) / (2(3))
4. Further factor the quadratic: (-6 ± 18) / 6
5. Solve for x: x = -4 or x = 3
Now, we need to determine if these points are maxima or minima by using the second derivative test:
6. Find the second derivative of the function: y'' = 6x + 6
7. Evaluate the second derivative at x = -4 and x = 3:
y''(-5) = 6(-4) + 6 = -18 (negative value indicates a maximum)
y''(3) = 6(3) + 6 = 24 (positive value indicates a minimum)
Therefore, we have a maximum at the value of x = -4.
Learn more about Maximum:
brainly.com/question/17467131
#SPJ11
(2x+1) -2 = (2x-1) -2 solve
Answers
Answer:
Ok
Step-by-step explanation:
-2 Cancel out from both sides
(2x + 1) = (2x - 1)
Kai the answer is 0= -2
Answer:
There is no solution.
Step-by-step explanation:
2x+1=2x-1
2x-2x=-1-1
0=-2
(02.02 LC)
If f(x) = 3(x + 4), find f(2).
I NEED HELP IMMEDIATELY
Answers
Answer:
f(2) = 18
Step-by-step explanation:
f(2) = 3(2 + 4)
f(2) = 3(6)
f(2) = 18
.
Koreans plz help mi ,Is Joon lee soo a girl or boy name???
Answers
Answer:
a boy name jaan hope helpful answer
Jen saves $20 for every $100 she earns
Answers
Answer:
y=100x-20x
Step-by-step explanation:
. Find f(3) for the following function
\(f(x)=3(2)^x+6\)
a.f(3) = 222
b.f(3) = 9
c.f(3) = 24
d.f(3) = 30
Answers
Answer:
\(\boxed {\boxed {\sf D. \ f(3)= 30}}\)
Step-by-step explanation:
We are given the function:
\(f(x)= 3(2)^x+6\)
We want to find f(3), so we must substitute 3 in for x.
\(f(3)= 3(2)^3+6\)
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction.
Solve the exponent first.
2³= 2*2*2= 4*2= 8\(f(3)= 3(8)+6\)
Multiply 8 and 3.
\(f(3)= 24+6\)
Add.
\(f(3)=30\)
For the function given, f(3) is 30.
I need help with these questions

Answers
ABC → CBA
XYZ → ZYX (not ZXY)
What values of b satisfy 4(3b + 2)^2 = 64?
Answers
Answer:
The value of 0 can satisfy b.
Step-by-step explanation:
4(3b + 2)^2 = 64
(12b + 8)^2 = 64
(12b + 8)^2 = 64
144b + 64 = 64
144b + 64 - 64 = 64 - 64
144b = 0
144b / 144 = 0 / 144
b = 0
So, the value of 0 can satisfy b.
Answer:
b = \(\frac{2}{3}\) or b = -2
Step-by-step explanation:
4(3b + 2)^2 = 64
Divide by 4 on both sides
(3b + 2)^2 = 16
Square root both sides
√(3b + 2)^2 = √16
3b + 2 = ±4
Subtract 2 on both sides
3b = ±4 - 2
Divide by 3 on both sides
b = (±4 - 2)/3
If 4 is positive, b is \(\frac{2}{3}\)
If 4 is negative, b is -2
A car salesperson has already sold 30 cars this year. He sells an average of 13 cars per month. Write an inequality to determine how many months, m, it will take for him to sell more than 60 cars.
Answers
Answer:
Step-by-step explanation:
We can use the inequality m * 13 > 60, where m is the number of months and 13 is the average number of cars sold per month. To solve for m, we can divide both sides of the inequality by 13: m > 60/13. This inequality tells us that it will take more than 4.6 months for the salesperson to sell more than 60 cars.
However, since m is a number of months, it is an integer. We need to round up this value, to ensure that the inequality is satisfied.
So the answer is m > 5 months.
HELP ME PLEASE!!
Which situation describes a quantity that increases by a constant percent rate?
The size of one photo is 15% larger than the size of another photo.
The population of one city is 85% greater than the population of another city.
The number of magazine subscribers each year is 15% greater than the previous year.
The number of plants in a pond is 85% of the number from the previous year
Answers
The situation that describes a quantity that increases by a constant percent rate is option C.
We can use the formula for exponential growth to represent a quantity that increases by a constant percent rate. For instance,
if we assume a starting value of N0 and a constant growth rate of r, the formula is given as N(t) = N0(1 + r)t.
This formula is an example of an exponential function. It means that the quantity increases by a constant percent rate over a given time.
The constant percent rate is equal to 100r percent. Therefore, we can see that option C is an example of a quantity that increases by a constant percent rate.
It states that the number of magazine subscribers each year is 15% greater than the previous year. This is a clear indication that the quantity is growing by a constant percent rate of 15%.
The quantity that increases by a constant percent rate is represented by an exponential function. The formula is given as N(t) = N0(1 + r)t. The situation that describes a quantity that increases by a constant percent rate is option C, which is the number of magazine subscribers each year is 15% greater than the previous year.
To know more about exponential growth visit:
brainly.com/question/1340582
#SPJ11
A taxi company charges $2.25 for the first mile and then $0.20 per mile for each additional mile, or F = $2.25 + $0.20(m - 1) where F is the fare and m is the number of miles.
if juan's taxi fare was $7.65 how many miles did he traavel in the taxi
Answers
Answer: Juan travelled 28 miles in the taxi
Step-by-step explanation:
A taxi company charges $2.25 for the first mile and then $0.20 per mile for each additional mile. This means that for m additional miles, the charge will be 2.25 + 0.20(m - 1)
So if F represents the fare, then
F = $2.25 + $0.20(m - 1)
If Juan's taxi fare was $7.65, to determine the number of miles that she paid for, we would substitute F = $7.65 into the equation,
F = $2.25 + $0.20(m - 1). It becomes
7.65 = 2.25 + 0.20(m-1)
7.65 = 2.25 + 0.20m - 0.20
7.65 - 2.25 + 0.20 = 0.2m
0.2m = 5.6
m = 5.6/0.2 = 28 miles
Answer:
Juan traveled 28 miles in the taxi
Step-by-step explanation:
7.65=2.25+0.2(m-1), subtract 2.25 from both sides, then you get 5.40=0.2(m-1)
then multiply 0.2 by the numbers in the parenthesis and get 5.40= 0.2m-0.2
add 0.2 to both sides to get 5.60 = 0.2m, divide both numbers by 0.2 and get 28 = m
Foundations of algebra

Answers
Answer:
D
Step-by-step explanation:
I tried to put in the explanation but I was told that I put in a link or inappropriate words. Neither is true, I do not know that I cannot put in the explanation.
find the difference 16.7-3.24
Answers
Answer: 13.46
Step-by-step explanation:
Subtract and you will get 13.46
Answer: 13.46
Step-by-step explanation:
how many 8-place license plates with 5 letters and 3 digits are possible if the only restriction is that all letters and numbers are unique? what if the 3 digits must be consecutive in the string?
Answers
For the first part, the number of license plates is: 65,780,800 and for the second part, the number of license plates with 3 consecutive digits is: 16,524,288.
How did we get these values?If there are no restrictions on where the digits and letters are placed, the number of 8-place license plates consisting of 5 letters and 3 digits with no repetitions allowed can be found using the permutation formula:
nPr = n! / (n-r)!
where n is the number of available characters (26 letters and 10 digits) and r is the number of characters needed for the license plate (8).
Therefore, the number of license plates is:
(26 P 5) x (10 P 3) = (26!/21!) x (10!/7!) = 65,780,800
If the 3 digits must be consecutive, there are 8 possible positions for the block of digits (either the first 3, second 3, or last 3). Once the position of the block is chosen, the number of license plates can be found by counting the number of ways to arrange the letters and the block of digits. The number of ways to arrange the letters is 26 P 5, and the number of ways to arrange the block of digits is 10 (since there are only 10 possible sets of consecutive digits).
Therefore, the number of license plates with 3 consecutive digits is:
8 x (26 P 5) x 10 = 16,524,288
learn more about permutation formula: https://brainly.com/question/1216161
#SPJ1
The complete question goes thus:
If there are no restrictions on where the digits and letters are placed, how many 8
-place license plates consisting of 5
letters and 3
digits are possible if no repetitions of letters or digits are allowed? What if the 3
digits must be consecutive?
