(Pls help)sally states that the equation g(x)= x^3 + 10^2 - 3x represents a quadratic function. Explain why she is incorrect.
Answers

Related Questions
Use the distributive property to find an expression equivalent to 24 + 64.
8(3 + 8)
6(4 + 8)
24 + (8)(8)
(2)(12) + (8)(8)
Please hurry
Answers
Answer:
8(3+8)
Step-by-step explanation:
The distributive property of multiplication states that
A(B+C) = A* B + A* C
Here, we can say that
8(3+8) = 8*3 + 8* 8 = 24 + 64. This seems correc,t but we can check the other options to make sure
6(4 + 8) = 6 * 4 + 6*8 = 24 + 48. This is incorrect
24 + (8)(8) . The 24 and 8 are not in the same parenthesis, so we cannot multiply them. Using PEMDAS, we multiply first, so 24+(8)(8) = 24 + 8*8 = 24 + 64. If there are multiple solutions, this can work. If not, this does not use the distributive property as we are not adding anything in the parenthesis.
Similarly, for (2)(12) + (8)(8), we are not adding anything in the parenthesis, but we can use PEMDAS to get 2*12 + 8*8 = 24 + 64, so this would also work but does not use the distributive property.
Find the value of x. X=?
Volume = 1500

Answers
Answer:
\(x=20\)
Step-by-step explanation:
Solve the following equation for x:
\(1500=1/3(15)^{2} x\)
Number 18. Please?!!!!

Answers
Answer:
The womans age is 25
mothers age is 50
Step-by-step explanation:
add those up and you get 75
Answer:
The woman is 25, and her mother is 50.
Step-by-step explanation:
The woman is half the mother's age.
That means the mother is twice the woman's age.
Let the woman's age be x
The mother's age is 2x.
The sum of the ages is 75.
x + 2x = 75
3x = 75
x = 25
2x = 2(25) = 50
Answer: The woman is 25, and her mother is 50.
2.
Find the rate of change for the situation. You run 7 miles in one hour and 21 miles in three hours.
A. 7 miles
B. 3 hours
C. 3 miles per hour
D. 7 miles per hour
Answers
Answer:
D. 7 miles per hour
Step-by-step explanation:
D. 7 miles per hour
A piece of wire of length
60
is cut, and the resulting two pieces are formed to make a circle and a square. Where should the wire be cut to (a) minimize and (b) maximize the combined area of the circle and the square?
Answers
The minimum area is 126.025 at \($x=\frac{60 \pi}{(4+\pi)}\) is 26.39, maximize the combined area of the circle and the square is 60.
Let the length of the wire (l)=60
Suppose the wire is cut into two parts as follows:
The length of the wire used for circle is x and the length of the wire used for square is (l-x)=(60-x).
So, length of the circle (x)= Perimeter of the of the circle
\($$(x)=2 \pi r$$\)
\($r=\frac{x}{2 \pi} \quad\) , r is the radius of the circular part.
Also, length of square (60-x)= Perimeter of the of the square
(60-x)=4 a
\($a=\frac{60-x}{4} \quad$\), a is the side of the square.
Hence, the total combined area of the circular region and the square region say A(x) is;
A(x)=area of circle + area of square
\(\\& A(x)=\pi r^2+a^2\end{aligned}$$\)
Put the values of 'r' and 'a' and proceed as follows;
\($$\begin{aligned}& A(x)=\pi\left(\frac{x}{2 \pi}\right)^2+\left(\frac{60-x}{4}\right)^2 \\& =\pi \frac{x^2}{4 \pi^2}+\left(15-\frac{x}{4}\right)^2\end{aligned}$$\)
\($=\frac{x^2}{4 \pi}+\left(15-\frac{x}{4}\right)^2$$\)
So, \($A(x)=\frac{x^2}{4 \pi}+\left(15-\frac{x}{4}\right)^2$\).
For optimization, find the Critical points of \($A^{\prime}(x)$\);
Differentiate \($A(x)=\frac{x^2}{4 \pi}+\left(15-\frac{x}{4}\right)^2$\) with respect to x;
\($$A^{\prime}(x)=\frac{2 x}{4 \pi}+2\left(15-\frac{x}{4}\right)\left(-\frac{1}{4}\right)$$\)
Put \($A^{\prime}(x)=0$\) for critical points;
\($$\begin{aligned}& A^{\prime}(x)=\frac{2 x}{4 \pi}+2\left(15-\frac{x}{4}\right)\left(-\frac{1}{4}\right)=0 \\& \frac{2 x}{4 \pi}=\left(15-\frac{x}{4}\right)\left(\frac{1}{2}\right) \\& \frac{4 x}{4 \pi}=\left(15-\frac{x}{4}\right) \\& \frac{4 x}{4 \pi}+\frac{x}{4}=15 \\& \frac{x(4+\pi)}{4 \pi}=15 \\& x=\frac{60 \pi}{(4+\pi)} \\& x=26.39\end{aligned}$$\)
x=26.39 is the required critical point.
For maximum or minimum, find \($A^{\prime \prime}(x)$\) as follows:
\($$\begin{aligned}& A^{\prime \prime}(x)=\frac{d}{d x}\left(\frac{2 x}{4 \pi}+\left(15-\frac{x}{4}\right)\left(-\frac{1}{2}\right)\right) \\& A^{\prime \prime}(x)=\frac{2}{4 \pi}+\frac{1}{8}\end{aligned}$$\)
As \($A^{\prime \prime}(x)=\frac{2}{4 \pi}+\frac{1}{8} > 0$\) for every value of x. So, \($A^{\prime \prime}(x) > 0$\) for every critical point.
Hence, by Second Derivative test; A(x) is minimum at \(\\ $$x=\frac{60 \pi}{(4+\pi)}$.\)
Therefore, minimum area is given as follows:
\($$\begin{aligned}& A\left(\frac{60 \pi}{(4+\pi)}\right)=\left(\frac{60 \pi}{(4+\pi)}\right)^2 \frac{1}{4 \pi}+\left(15-\frac{60 \pi}{4(4+\pi)}\right)^2 \\\\& \text { As } x=\frac{60 \pi}{(4+\pi)}=26.39\end{aligned}$$\)
So,
\($$\begin{aligned}& A\left(\frac{60 \pi}{(4+\pi)}\right)=\left(\frac{60 \pi}{(4+\pi)}\right)^2 \frac{1}{4 \pi}+\left(15-\frac{60 \pi}{4(4+\pi)}\right)^2 \\& A(26.39)=(26.39)^2 \frac{1}{4 \pi}+\left(15-\frac{26.39}{4}\right)^2 \\& A(26.39)=55.42030+70.6020 \\& A(26.39)=126.025\end{aligned}$$\)
Therefore, the minimum area is 126.025 at \($x=\frac{60 \pi}{(4+\pi)}\) is 26.39.
b. Note that, maximum area cannot be determined by the critical points as there is only one critical point that too corresponds to the minimum area.
For maximum area; consider the following;
Put x=0 and x=60 in A(x);
\($$\begin{aligned}& A(0)=(0)^2 \frac{1}{4 \pi}+\left(15-\frac{0}{4}\right)^2 \\& A(0)=(15)^2 \\& A(0)=225 \\& A(60)=(60)^2 \frac{1}{4 \pi}+\left(15-\frac{60}{4}\right)^2 \\& A(60)=(60)^2 \frac{1}{4 \pi} \\& A(60)=286.47\end{aligned}$$\)
So, at x=60, A(x) is maximum. That is in the case, when total length of the wire is used for circle.
For more such questions on Perimeter of circle & square
https://brainly.com/question/18485211
#SPJ4
Simplify each expression
8a-4a
Answers
Answer: 4a
Step-by-step explanation:
Answer:
4a
Step-by-step explanation:
8 of something minus 4 of something gives you 4 of that thing
Student A is 15 years old. Student B is one-third older. How many years ago was student B
twice as old as student A?
A) 5
B) 7
C) 9
D) 10
Answers
Answer:
D
Step-by-step explanation:
one third of 15 is 5
15 + 5 = 20
Student B is 20 years old, 5 years older than student A
10 years ago, Student B was 10 and Student A was 5.
The number of years ago was student B twice as old as student A should be 10 when the student A age is given.
Calculation of the number of years:Since
Student A is 15 years old. Student B is one-third older
One-third of 15 should be 5
So, total be like
= 15 + 5
= 20
So, the number of years be like
= 20 - 10
= 10
hence, The number of years ago was student B twice as old as student A should be 10.
learn more about age here: https://brainly.com/question/10189250
This sample is selected by dividing the population into subgroups and then taking a fixed number of units from each group using the simple random sample. simple random sample stratified random sample cluster random sample Voluntary random sample
Answers
The correct sampling method described in the question is a stratified random sample among the simple random sample, stratified random sample, cluster random sample and Voluntary random sample
The sampling method described in the question is a stratified random sample.
In a stratified random sample, the population is divided into subgroups or strata based on certain characteristics or criteria. Then, a random sample is selected from each stratum. The key idea behind this method is to ensure that each subgroup is represented in the sample proportionally to its size or importance in the population. This helps to provide a more accurate representation of the entire population.
In the given sampling method, the population is divided into subgroups, and a fixed number of units is taken from each group. This aligns with the process of a stratified random sample. The sample selection is random within each subgroup, but the number of units taken from each group is fixed.
Other sampling methods mentioned in the question are:
Simple random sample: In a simple random sample, each unit in the population has an equal chance of being selected. This method does not involve dividing the population into subgroups.
Cluster random sample: In a cluster random sample, the population is divided into clusters or groups, and a random selection of clusters is included in the sample. Within the selected clusters, all units are included in the sample.
Voluntary random sample: In a voluntary random sample, individuals self-select to participate in the sample. This method can introduce bias as those who choose to participate may have different characteristics than those who do not.
Therefore, the correct sampling method described in the question is a stratified random sample.
Learn more about sampling methods here:
https://brainly.com/question/15604044
#SPJ4
The area of a triangular sign is 36 ft.². If the base of the sign is 12 feet, what is the height of the sign?
Answers
Answer:
The height of the sign is 6 feet.
Step-by-step explanation:
Area of triangle is base times height divided by 2 ( b x h ÷ 2 ), so we just rearrange that.
A = \(\frac{bh}{2}\)
36 = 12 x h ÷ 2
36 x 2 = 12 x h
72 = 12 x h
72 ÷ 12 = h
6 = h
h = 6
Evaluate each expression
1. 3x(-96)÷12+9
Answers
Answer:
-24+9
Step-by-step explanation:

3. Your boss asks you to compare three phone plans. Identify the cheapest plan when an average of 190 text messages are sent each month. • Plan A costs a basic fee of $29.95 per month and 13 cents per text message • Plan B costs a basic fee of $53.00 per month and has unlimited text messages. • Plan C has no basic fee, but charges $0.28 per text message. 2021 Illuminate Education. Inc
Answers
Analyze each plan according to the given specifications.
Plan A:
The basic fee must be added to the product of 0.13 and the average messages sent.
\(29.95+190\cdot0.13=54.65\)Plan B:
It already includes the cost for unlimited messages.
\(53.00\)Plan C:
The plan costs the product of 0.28 and the average messages sent.
\(190\cdot0.28=53.2\)When comparing these plans, the cheapest one is Plan B, which only costs $53.00.
Ellis weighs 7 stone and 5 pounds. Ed weighs 50 kilograms. 1 kg is Which of the two is heavier and by how much?
Answers
The ellis weight is heavier and by 7.23 lbs.
We are given that;
Weight= 5pounds
Now,
To convert Ed’s weight from kilograms to pounds, we can multiply by the conversion factor of 2.20462262185. We get:
Ed’s weight in pounds = 50 kg * 2.20462262185 lbs/kg Ed’s weight in pounds = 110.2311310925 lbs
To convert Ellis’s weight from stones and pounds to pounds, we can multiply the number of stones by 14 and add the number of pounds. We get:
Ellis’s weight in pounds = 7 stones * 14 lbs/stone + 5 lbs Ellis’s weight in pounds = 98 + 5 Ellis’s weight in pounds = 103 lbs
To compare the weights, we can subtract them and see which one is larger. We get:
Ed’s weight - Ellis’s weight = 110.2311310925 lbs - 103 lbs Ed’s weight - Ellis’s weight = 7.2311310925 lbs
Therefore, by unitary method the answer will be 7.23 lbs.
Learn more about the unitary method, please visit the link given below;
https://brainly.com/question/23423168
#SPJ1
In 2011, a train carried 8% more passengers than in 2010. In 2012, it carried 8% more passengers than in 2011. Find the percentage increase in the number of train passengers from 2010 to 2012
Answers
Answer:
There was a 16% increase since 2010 to 2012.
Step-by-step explanation:
8% + 8% = 0.16 x 100 = 16%.
Jacob trims trees and mows lawns during the summer months he earns 50$ per lawn and 120$ per tree he wants to purchase a car for 4,500if Jacob plans to mow 45 lawns this summer how many trees must he trim to earn at least 4,500
Answers
Answer:
at least 19
Step-by-step explanation:
Let t represent the number of trees Jacob needs to trim. He wants ...
50(45) +120t ≥ 4500
120t ≥ 2250 . . . . . . . . . subtract 2250
t ≥ 18.75
Jacob must trim at least 19 trees to earn at least $4500.
1.HELP FAST
-6(2x + 1) < 5- (x – 4)-6x
Interval Notation:
Answers
Answer:
(-3, ∞).
Step-by-step explanation:
-6(2x + 1) < 5- (x – 4)-6x
-12x - 6 < 5 - x + 4 - 6x
-12x + x + 6x < 5 + 4 + 6
-5x < 15
x > 15/-5 (note that the inequality sign flips when dividing by a negative)
x > -3.
Explain the steps to locate the average rate of change when two points are displayed on an exponential graph. -
Answers
Answer:
Explanation: The rate of change between two points on a curve can be approximated by calculating the change between two points. Let be the coordinates of the first point and be the coordinates of the second point. Then the formula giving approximate rate of change is
Step-by-step explanation:
calculating the change between two points.
Try These.
2/3*(-7)8.
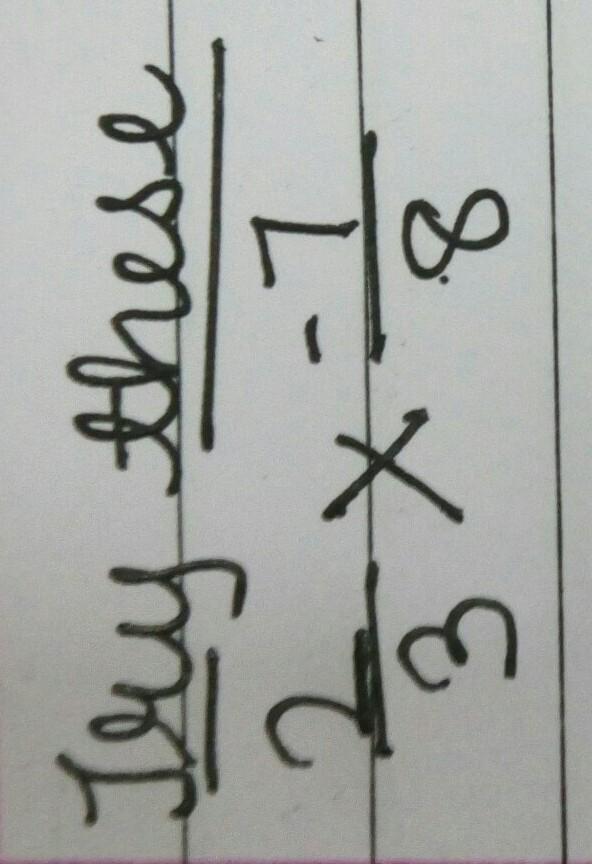
Answers
Answer:
-7/12
Step-by-step explanation:
2/3×-7/8
= -7/12
Answer:
-7/12
Step-by-step explanation:
2/3×(-7)/8
2×(-7) = -14
3×8 = 24
-14/24= -7/12
Geometry problem pls help

Answers
Find an equation of the tangent plane to the given surface at the specified point. z = 5(x - 1)^2 + 4(y + 3)^2 + 4, (2, -2, 13) z = ______
Answers
The equation of the tangent plane to the given surface at the specified point is z = 10x + 8y + 6.
To find an equation of the tangent plane to the given surface at the specified point (2, -2, 13), we need to first take partial derivatives of the given function.
Taking partial derivatives with respect to x and y, we get:
∂z/∂x = 10(x-1)
∂z/∂y = 8(y+3)
Next, we plug in the given point (2, -2, 13) into the partial derivatives to find the slope of the tangent plane:
∂z/∂x = 10(2-1) = 10
∂z/∂y = 8(-2+3) = 8
So the slope of the tangent plane at the given point is (10, 8).
Now we need to find the intercept of the tangent plane by plugging in the point (2, -2, 13) into the original function:
z = 5(2-1)^2 + 4(-2+3)^2 + 4 = 13
Therefore, the equation of the tangent plane is:
10(x-2) + 8(y+2) = z-13
Or rearranging,
10x + 8y - z = -6
For more about tangent plane:
https://brainly.com/question/31397815
#SPJ11
Need help with Geometry proof--thank u

Answers
Step-by-step explanation:
QR is parallel to TU | Given
S is the midpoint of QT | Given
QS = ST | Definition of midpoint
<QSR = <TSU | definition of vertical angles
<QRS = <STU | Definition of Alternate Interior Angles
QSR = TSU | ASA
Pretty sure that's right :D
Also, wherever it says "=", I mean congruency symbol
The difference between 8 forty-sevens and 7 forty-sevens.
Answers
Answer:
47
Step-by-step explanation:
No matter what number you do if there is one left then it's that number
So dif between 8 and 7 is 1
1*47 = 47
determine the angle between 0 and 2π that is coterminal with 17pi/4
Answers
the angle between 0 and 2π that is coterminal with 17π/4 is π/4.
To find the angle between 0 and 2π that is coterminal with 17π/4, we need to find an equivalent angle within that range.
Coterminal angles are angles that have the same initial and terminal sides but differ by a multiple of 2π.
To determine the coterminal angle with 17π/4, we can subtract or add multiples of 2π until we obtain an angle within the range of 0 to 2π.
Starting with 17π/4, we can subtract 4π to bring it within the range:
17π/4 - 4π = π/4
The angle π/4 is between 0 and 2π and is coterminal with 17π/4.
what is equivalent'?
In mathematics, the term "equivalent" is used to describe two things that have the same value, meaning, or effect. When two mathematical expressions, equations, or statements are equivalent, it means that they are interchangeable and represent the same mathematical concept or relationship.
To know more about angle visit:
brainly.com/question/31818999
#SPJ11
You invested $28,000 in two accounts paying 6% and 8% annual interest, respectively. If the total interest earned for the year was $2100, how much was invested at each rate?
Answers
Answer:
At 6% interest rate, amount invested = $7000
At 8% interest rate, amount invested = $21000
Step-by-step explanation:
Let amount invested in one account be x and amount invested in the other be y.
Thus;
x + y = 28000 - - - - (eq1)
Interest rate for them are 6% and 8% annually.
We are told that total interest earned for the year was $2100
Thus;
0.06x + 0.08y = 2100 - - - - (eq 2)
Make x the subject in equation 1.
x = 28000 - y - - - - (eq 3)
Put 28000 - y for x in eq 2
0.06(28000 - y) + 0.08y = 2100
1680 - 0.06y + 0.08y = 2100
0.02y = 2100 - 1680
0.02y = 420
y = 420/0.02
y = 21000
Put 21000 for y in eq 3 to get;
x = 28000 - 21000
x = 7000
Thus amount invested in each account is;
At 6% interest rate, amount invested = $7000
At 8% interest rate, amount invested = $21000
\(f(x) = \sqrt{9 - {x}^{2} } \)
I have a doubt. I know that the domain will be [-3, 3] because this is a real function. But what will be the range. Everywhere it is given as [0, 3]. But shouldn't it be [-3, 3].
For example let x = 0, then f(x) = √9, and it can be either -3 or 3. Why are we considering just the positive value?
Please explain.
Answers
Answer:
range of f is [0,3]
Step-by-step explanation:
The "square root" symbol, \(\sqrt{\text{ \quad }}\), is a function. As a result, it only has a single output because functions must only have a single output for each input.
Thinking about it graphically, if the square root function did give both a positive and a negative result, the function "f" would not pass the vertical line test and it would not be a function.
When solving an equation like \(x^2=25\), to solve, we must apply the square root property. The square root property says that to find both solutions, one must look at both the positive and the negative of the square root. So, to solve:
\(x^2=25\)
Apply square root property...
\(\sqrt{x^2} = \pm \sqrt{25}\)
\(x=\sqrt{25}\) or \(x=-\sqrt{25}\)
\(x=5\) or \(x=-5\)
In this case, because the square root function itself only outputs non-negative results (so, including zero, as you already identified), the range will only be [0,3].
One solution to a quadratic function, g, is given.
9 - √2i
Which statement is true?
A. Function g has no other solutions.
B. The other solution to function g is -9 + √2i
.
C. The other solution to function g is -9 - √2i
.
D. The other solution to function g is 9 + √2i
.
Answers
Answer:
D. The other solution to function g is 9 + √2i
Step-by-step explanation:
The roots of a quadratic equation of the form ax² + bx + c = 0
are
\(x = -\dfrac{b}{2a} + \dfrac{\sqrt{b^2-4ac}}{2a}\\and\\x = -\dfrac{b}{2a} - \dfrac{\sqrt{b^2-4ac}}{2a}\\\)
If one of the roots is 9 - √2i then
\(-\dfrac{b}{2a} = 9\)
and
\(\dfrac{\sqrt{b^2-4ac}}{2a} = 2i\)
So if one root is 9 - √2i then the other root must be 9 -+ 2i
This is answer choice D
5x + 12 = 2x + 21
Step by step
(Right answer plz )
Answers
Answer:
\(5x + 12 = 2x + 21 \\ 5x - 2x = 21 - 12 \\ 3x = 9 \\ x = \frac{9}{3} \\ x = 3\)
Step-by-step explanation:
please mark me brainliest
Answer:
\(5x + 12 = 2x + 21 \\ 5x - 2x = 21 - 12 \\ 3x = 9 \\ x = \frac{9}{3}\\ \boxed{x = 3}\)
x = 3 is the right answer.What is the solution of the system of equations?
13x-6y=2
3x-4y=-10
(Write as ordered pair)
Answers
Step-by-step explanation:
let's multiply the first equation by 2 and the second equation by -3, and then we add them together :
26x - 12y = 4
-9x +12y = 30
-------------------------
17x 0 = 34
x = 2
and now we use one of the original equations to solve for y :
3×2 - 4y = -10
6 - 4y = -10
-4y = -16
y = 4
the solution is (2, 4).
Help me please!! This is timed and I’m stuck

Answers
Answer:
D is the correct answer
Step-by-step explanation:
Answer:
B. 13/2Step-by-step explanation:
Given equation:
2x² + 7x - 15 = 0It has roots r and s.
We know how to find the sum and product of roots.
Sum of roots:
r + s = -7/2Product of roots:
rs = -15/2Use the above two equations to work out the value of r - s:
\(r - s = \sqrt{(r - s)^2} =\)\(\sqrt{(r+s)^2-4rs} =\)\(\sqrt{(-7/2)^2-4(-15/2)} =\)\(\sqrt{169/4} =13/2\)Correct choice is B
The rear window of DeMarcus's car is in the shape of a trapezoid. The bottom is 50 inches across and the top is 45 inches across. The window has a height of 24 inches. What is the area of the window?
Answers
Answer:
1140 square inches
Step-by-step explanation:
The rear window of DeMarcus's car is in the shape of a trapezoid. The bottom is 50 inches across and the top is 45 inches across. The window has a height of 24 inches. What is the area of the window?
Area of a Trapezoid
= 1/2(b1 + b2)h
b1 =
b2 =
h =
Hence, 1/2 (50 + 45) × 24
= 1/2 × 95 × 24
= 1140 Square inches
f
is inversely proportional to
√
g
.
When
f
=
10
,
g
=
121
Work out
f
when
g
=
25
Answers
Answer:
f = 22
Step-by-step explanation:
From the question
\(f \alpha \: \frac{1}{ \sqrt{g} } \)
Meaning, f is inversely proportional to √g
Therefore,
\(f \: = \: \frac{k}{ \sqrt{g} } \)
Where, k is constant
Making k subject of the formula,
k = f·√g
Slotting our values of f = 10, when g = 121,
k = 10·√121
k = 10·11
k = 110
Now that we have our constant,
To find f when g = 25,
\(f \: = \: \frac{k}{ \sqrt{g} } \)
Slotting in,
k = 110, g= 25,
We have,
f = 110/√25
f = 110/5
f = 22, when g=25