Answers
Answer:
i need help also
Step-by-step explanation:
Answer:
B, C, A
Step-by-step explanation:
I did this question before and I got it right.
Related Questions
( hurry!!) Is the system of equations consistent and independent, consistent and dependent, or inconsistent?
y=3x+4 y=3x+3
Select the correct answer from the drop-down menu.
Answers
Answer:
I think it's the 2nd one B but im not completely sure
Step-by-step explanation:
Answer: Inconsistent
Step-by-step explanation:
y = 3x + 4 → m = 3, b = 4
y = 3x + 3 → m = 3, b = 3
These equations have the same slope but different y-intercepts so they are parallel lines which means they will never intersect.
NOTES
one solution: consistent & independent lines cross
infinite solutions: consistent & dependent same line
no solution: inconsistent parallel lines
what is the pattern rule for 1. 25, 1, 0.75, 0.50,0.25
Answers
Answer:
-0.25n + 1
Step-by-step explanation:
Difference between all numbers: -0.25
Hence,
\(t_n = -0.25n + 1\)
Feel free to mark it as brainliest :D
Solve the equation for the specified variable.
S-BA-8, for B
B=
Answers
When the equation is solved for B, the equivalent equation is B = 8/A
How to solve the equation for variable B?The equation is given as:
BA = 8
To solve for the variable B, we simply divide both sides by A
So, we have:
BA/A = 8/A
Evaluate the expression on the right-hand side
BA/A = 8/A
Evaluate the expression on the left-hand side
B = 8/A
Hence, when the equation is solved for B, the equivalent equation is B = 8/A
Read more about equations at:
https://brainly.com/question/2972832
#SPJ1
sheri’s cab fare was $32, with a 20% gratuity and no taxes. sheri's write a check to the cab driver for $40. is this a reasonable amount? explain.
Answers
In a case whereby sheri’s cab fare was $32, with a 20% gratuity and no taxes. sheri's write a check to the cab driver for $40, this can be considered as being reasonable amount because it is $1.60 more to the cab driver.
How can we know if it is reasonable?A gratuity is a sum of money that customers typically give to specific service sector employees, including those in the hotel industry, in addition to the service's base charge for the work they have completed.
Given ; Sheri’s cab fare was $32 and the percentage of gratuity is 20%
amount of gratuity = 20% 0f 32 = 6.40
The fare of the cab + gratuity = 32 + 6.40 = 38.40
Check to the cab driver for $40 , implies ($40 - $38.40)= $1.60 more to the cab driver.
Hence, it is reasonable.
Learn more about amount at;
https://brainly.com/question/11158699
#SPJ1
farmer ed has meters of​ fencing, and wants to enclose a rectangular plot that borders on a river. if farmer ed does not fence the side along the​ river, what is the largest area that can be​ enclosed?
Answers
The largest area that can be enclosed with 6,500 meters of fencing without fencing the side along the river is approximately 1,083,333.33 square meters.
To find this answer, we can use the formula for the area of a rectangle, A = lw, where l is the length of the rectangle and w is the width of the rectangle.
Since we are not fencing the side along the river, the rectangle has three sides that are each of length x, and one side that is the length of the river, which we can call y. We know that the perimeter of the rectangle is 6,500 meters, so:
3x + y = 6,500Solving for y, we get:
y = 6,500 - 3xNow we can substitute y into the formula for the area of a rectangle:
A = lw = x(6,500 - 3x)Expanding this expression, we get:
A = 6,500x - 3x²
To find the maximum value of A, we can take the derivative of A with respect to x and set it equal to zero:
dA/dx = 6,500 - 6x = 0
Solving for x, we get:
x = 1,083.33
Substituting x back into the equation for y, we get:
y = 6,500 - 3(1,083.33) = 2,250.01Therefore, the largest area that can be enclosed is approximately:
A = 1,083.33(2,250.01) = 1,083,333.33 square meters.
Learn more about Area
https://brainly.com/question/25292087
#SPJ4
Complete Question:
Farmer Ed has 6,500 meters of fencing and wants to enclose a rectangular plot that borders on a river. If Farmer Ed does not fence the side along the river, what is the largest area that can be enclosed?
helpppppppppppppppppppppppppppppppppppppppppppppppppp
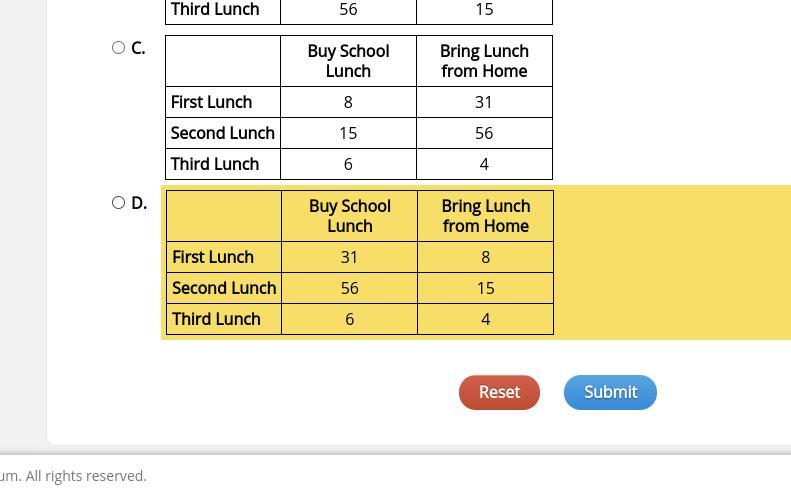

Answers
Answer:
A!!!!!!!!!!!!!!!!!!
Maya will deposit $1,650 in an account that earns 5% simple interest every year. Her brother, James, will deposit $1,600 in an account that earns 8% interest compounded annually. The deposits will be made on the same day, and no additional money will be deposited or withdrawn from the accounts. Compare and contrast the two siblings' accounts after four year
Answers
Answer:
Step-by-step explanation:
Step one:
given data
Maya
P=$1650
r=5%= 0.05
t= 4 years
The simple interest expression is
A=P(1+rt)
A=1650(1+0.08*4)
A=1650(1+0.32)
A=1650(1.32)
A=1650*1.32
A=$2178
James
P=$1600
r=8%= 0.08
t=4years
The compound interest expression is
A=P(1+r)^t
A=1600(1+0.08)^4
A=1600(1.08)^4
A=1600*1.360
A=$2176
After 4 years Mayas' balance is $2178
After 4 years James' balance is $2176
the difference is =2178-2176=$2
100PTS!!! MATH HELP PLZ??!!
Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Then find the area of the region.
y=1/x,y=1/x2,x=6
i tried to use the antiderivative but when i plug 0 in, it turns out ln(6)+1/6-ln(0)-1/0 and i dont know what to do with 1/0 :(
Answers
Answer:
\(\displaystyle \int_1^6\left|\frac{1}{x}-\frac{1}{x^2}\right|dx=\ln|6|-\frac{5}{6}\)
Step-by-step explanation:
We'll integrate with respect to x.
Recall that the area between some \(f(x)\) and some \(g(x)\) on the interval \([a, b]\) is given by:
\(\displaystyle \int_a^b|f(x)-g(x)|dx\)
The function \(x=6\) will be the upper bounds of our definite integral. The lower bounds will be the intersection of \(\displaystyle y=\frac{1}{x}\) and \(\displaystyle y=\frac{1}{x^2}\). Set the functions equal to each other and solve for x:
\(\displaystyle \frac{1}{x}=\frac{1}{x^2},\\\\x^2=x,\\x=1\)
Therefore, we'll be integrating the area between \(\displaystyle \frac{1}{x}\) and \(\displaystyle \frac{1}{x^2}\) on the interval \([1, 6]\). In integral notation, this is:
\(\displaystyle \int_1^6\left|\frac{1}{x}-\frac{1}{x^2}\right|dx\)
To evaluate this integral, recall that \(\displaystyle \int \frac{1}{x}dx=\ln|x|+C\) and \(\displaystyle \int \frac{1}{x^2}dx=\int x^{-2}dx=-x^{-1}+C=-\frac{1}{x}+C\).
Therefore,
\(\displaystyle \int_1^6\left|\frac{1}{x}-\frac{1}{x^2}\right|dx=\int_1^6\ln|x|-\left(-\frac{1}{x}\right)dx=\int_1^6\ln|x|+\frac{1}{x}dx\)
Solving yields:
\(\displaystyle\left \left(\ln|x|+\frac{1}{x}\right) \right \vert_1^6=\ln|6|+\frac{1}{6}-\left(\ln|1|+\frac{1}{1}\right)=\ln|6|+\frac{1}{6}-0-1=\boxed{\ln|6|-\frac{5}{6}}\)
Answer:
\(\ln 6 - \dfrac{5}{6}\)
Step-by-step explanation:
To find the area enclosed by curves and lines, use definite integration:
\(\displaystyle \int^b_a \text{f}(x)\:\:\text{d}x \quad \textsf{(where a is the lower limit and b is the upper limit)}\)
Definite integrals have limits. The limits tell you the range of x-values to integrate the function between.
Given functions:
\(\begin{cases}y=\dfrac{1}{x}\\\\y=\dfrac{1}{x^2}\end{cases}\)
The upper limit has been given as x = 6.
The lower limit is the point of intersection of the two curves.
To find the lower limit, equate the functions and solve for x:
\(\implies \dfrac{1}{x}=\dfrac{1}{x^2}\)
\(\implies x=1\)
Therefore, the limits for this integration are x = 1 and x = 6.
To find the area enclosed by the two curves, the point of intersection and the line x=3, integrate the areas under both curves using definite integration and subtract the area under the lower curve from the area under the upper curve.
\(\begin{aligned}\displaystyle \int^6_1 \dfrac{1}{x}\:\:dx-\int^6_1 \dfrac{1}{x^2}\:\:dx & = \int^6_1\left(\dfrac{1}{x}-\dfrac{1}{x^2}\right)\:\:dx \\\\& = \int^6_1\left(\dfrac{1}{x}-x^{-2}\right)\:\:dx\\\\& = \left[\ln |x| + \dfrac{1}{x} \right]^6_1\\\\& = \left(\ln 6 + \dfrac{1}{6} \right) - \left(\ln 1 + \dfrac{1}{1} \right)\\\\& = \left(\ln 6 + \dfrac{1}{6} \right) - \left(0 +1\right)\\\\& = \ln 6 -\dfrac{5}{6}\end{aligned}\)
Integration Rules
\(\boxed{\begin{minipage}{4 cm}\underline{Integrating $x^n$}\\\\$\displaystyle \int x^n\:\text{d}x=\dfrac{x^{n+1}}{n+1}+\text{C}$\end{minipage}}\)
Increase the power by 1, then divide by the new power.
\(\boxed{\begin{minipage}{3.5 cm}\underline{Integrating $\frac{1}{x}$}\\\\$\displaystyle \int \dfrac{1}{x}\:\text{d}x=\ln |x|+\text{C}$\end{minipage}}\)
Learn more about integration here:
https://brainly.com/question/27805589
https://brainly.com/question/27954290

Arthur paid $0.84 for 0.25 pound of potato salad. How much does one pound cost?
Answers
Step-by-step explanation:
1 pound is 4 times 0.25 pounds.
$0.84 = 0.25 pounds
1 pound = $0.84 times 4
1 pound = $3.36
Answer:
$3.36 per pound
Step-by-step explanation:
The information gives us that 1/4 a pound of salad costs $0.84, to get to one pound all we have to do is multiply $0.84 by 4 to get our pound price.
0.84*4= $3.36
Brainliest would be appreciated! :-)
A rock is tossed from a platform and follows a parabolic path through the air. The height of the rock in metres is given by h(t) = -5t² + 12t + 14 where t is measured in seconds. a) How high is the rock off the ground when it is thrown? b) How long is the rock in the air? c) For what times is the height of the rock greater than 17 metres? d) How long is the rock above the height of 17 metres?
Answers
Given information:h(t) = -5t² + 12t + 14 where t is measured in seconds.a) How high is the rock off the ground when it is thrown?For h(0), the initial height of the rock is required.h(0) = -5(0)² + 12(0) + 14 = 14 meters.
For h(t), the rock's maximum height needs to be found to determine the time when the rock hits the ground. In order to determine the maximum height, first, we need to find the time of maximum height using the formula:
tmax = -b/2a = -12/2(-5) = 1.2s
Now, h(1.2) can be found to determine the maximum height:
h(1.2) = -5(1.2)² + 12(1.2) + 14 = 20.8 meters
Therefore, the rock is in the air for (1.2*2) 2.4 seconds.c) For what times is the height of the rock greater than 17 metres?This means h(t) > 17. Solving this inequality gives:-
5t² + 12t + 14 > 17
=> -5t² + 12t - 3 > 0
=> (-5t + 3)(t - 1) > 0
From part c, we know that the rock's height is greater than 17 metres between 0 and 0.6 seconds and after 1 second. Therefore, the time the rock is above 17 metres is the sum of these two time periods:0.6 seconds + (2 - 1) seconds = 1.6 seconds.
To know more about inequality visit:-
https://brainly.com/question/28823603
#SPJ11
Find the surface area of the pyramid. 4.33 m 5 m 5 m The surface area is (Type a whole number or a decimal

Answers
Answer:
43.3 m²
Explanation:
The surface area of the pyramid can be calculated as 4 times the area of one face.
So, the area of one face is equal to:
\(A=\frac{1}{2}\cdot b\cdot h\)Where b is the base of the triangles and h is the height. So, replacing b by 5 m and h by 4.33 m, we get:
\(\begin{gathered} A=\frac{1}{2}\cdot5\text{ m }\cdot4.33\text{ m} \\ A=10.825m^2 \end{gathered}\)So, the surface area is equal to:
\(A=4(10.825)=43.3m^2\)Therefore, the answer is 43.3 m²
4. Give an equation of the surface of revolution generated by revolving x = (1/z )^z about the z-axis.
Answers
The equation of the surface of revolution generated by revolving x = (1/z)^z about the z-axis is x = e^(-y).
To find the equation of the surface of revolution, we start with the parametric equation x = (1/z)^z, y = t, z = t. We eliminate the parameter t by substituting z for t in the equation x = (1/z)^z. Simplifying further, we obtain x = e^(-y).
This equation represents the surface of revolution generated by revolving the curve x = (1/z)^z about the z-axis. The exponentiation by e^(-y) signifies that the x-coordinate changes exponentially as the y-coordinate varies.
Therefore, as we revolve the curve around the z-axis, it forms a surface with an exponential decay in the x-direction. Hence, the equation x = e^(-y) describes the surface of revolution.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ11
You need 50, 4ounce portions of green beans. Fresh green beans yield 85% edible product after they have been cleaned and trimmed. How many pounds of fresh green beans do you need to purchase? 2. You need ten pounds of fish for stew. The whole fish you are purchasing has a 40% yield after it has been cleaned. How much whole fish do you need to purchase? 3. You are serving a half-pound strip sirloin for a special. Your forecast projects that 60 people will order sirloin, so how many pounds of sirloin should you bring in if, after trimming, you usually have 20% waste?
Answers
1. To have 50, 4-ounce portions of green beans, we need to find how many pounds of fresh green beans should be bought.
Firstly, we'll need to find out how many ounces are needed to have a total of 50 portions of 4-ounces each.
50 portions of 4 ounces each = 50 × 4 = 200 ounces.
To find the total weight in ounces of the green beans that need to be purchased, we divide 200 by 0.85 (as 85% of fresh green beans are edible) as follows:
Total weight in ounces = 200/0.85 = 235.29 ounces.
1 pound is equal to 16 ounces, so to find the total weight in pounds of fresh green beans, we divide 235.29 by 16 as follows:
Total weight in pounds = 235.29/16 = 14.7 pounds.
Therefore, approximately 15 pounds of fresh green beans should be purchased.
2. We need to find out how much whole fish we need to buy to obtain 10 pounds of fish after it has been cleaned (with 40% yield).
We can solve for this using the formula: Yield% = (edible portion ÷ raw portion) × 100.
We can rearrange the formula as: Edible portion = (yield% ÷ 100) × raw portion
We need a 40% yield, so substituting the given values in the formula above, we get:
Edible portion = (40 ÷ 100) × Raw portion
Let's say Raw portion is R. We need 10 pounds of edible portion, so:
10 pounds = (40 ÷ 100) × R10 ÷ (40 ÷ 100) = R25 = R
Therefore, 25 pounds of whole fish should be purchased.
3. We are serving 60 people with half-pound strip sirloin, so we need to find how many pounds of sirloin should be brought in, assuming that 20% of it will be wasted after trimming.
Each serving requires a half-pound, so 60 people need a total of 60 × 0.5 = 30 pounds of sirloin.
To find out the total weight of sirloin that should be brought in, we can use the formula:
Total weight of sirloin = Required weight of sirloin ÷ (1 - Waste%)
Required weight of sirloin = 30 pounds
Waste% = 20% = 0.2
Substituting these values into the formula, we get:
Total weight of sirloin = 30 ÷ (1 - 0.2)= 30 ÷ 0.8= 37.5 pounds.
So, approximately 38 pounds of sirloin should be brought in.
Learn more about purchasing at
https://brainly.com/question/24112214
#SPJ11
the typing speeds for the students in a typing class is normally distributed with mean 44 (μ) words per minute and standard deviation 6 (σ) words per minute. what is the probability that a randomly selected student has a typing speed of less than 38 words per minute? use the empirical rule provide the final answer as a percent. if necessary round the percent to the nearest whole number.
Answers
The probability that a randomly selected student has a typing speed of less than 38 words per minute is 15.87%.
What is normal distribution?
A probability distribution that is symmetric about the mean is the normal distribution, sometimes referred to as the Gaussian distribution. It demonstrates that data that are close to the mean occur more frequently than data that are far from the mean. The normal distribution appears as a "bell curve" on a graph.
The formula for z-score is z = (x -μ)/σ
Where,
Z is standard score.
x is observed value.
μ is mean of the sample.
σ is standard deviation of the sample.
According to the given question.
The mean of the distribution is μ = 44
The standard deviation of the distribution is σ = 6
The observed value is x = 38
Therefore, z-score = (38 -44)/6 = -1
So, the are P(z > -1) = 15.87%
Hence, the probability that a randomly selected student has a typing speed of less than 38 words per minute is 15.87%.
To learn more about z-score and probability, click on below link:
https://brainly.com/question/14174044
#SPJ4
9y+3-y please help
i beg
Answers
Answer:
9
Step-by-step explanation:
Micah is 111 of 282828 students in a class. micah's teacher is going to randomly select 333 students from their class to visit a classroom of younger students. what is the probability micah is included in the group of students chosen? choose 1 answer:
Answers
The probability that micah is included in the group of students chosen is ²⁸²⁸²⁸C₃₃₂ / ²⁸²⁸²⁸C₃₃₃
According to the question,
Total number of students in class = 282828
Micha's roll number = 111
Micha's teacher is randomly selecting students
Number of students to be selected = 333
So , Total number of ways to select 333 students from 282828 is
=> ²⁸²⁸²⁸C₃₃₃
Now , We have to find the probability that micah is included in this sample.
So, Lets fixed the place of micah
Number of students left after fixing micah place = 333 - 1
=> 332
Number of ways to select these 332 = ²⁸²⁸²⁸C₃₃₂
Therefore , Probability = ²⁸²⁸²⁸C₃₃₂ / ²⁸²⁸²⁸C₃₃₃
To know more about Probability here
https://brainly.com/question/9793303
#SPJ4
find the volume common to two spheres, each with radius r, if the distance between their centers is r/2.
Answers
The volume common to two spheres, each with radius r, if the distance between their centres is r/2 is V = (11/12)×π×r³.
The attached diagram shows 2 circumferences with radius r and separated centres by r/2.
Let´s call circumferences 1 and 2; by symmetry, rotating area A will produce a volume V₁ identical to a V₂, Obtained by rotating area B ( both around the x-axis), then the whole volume V will be:
V = 2× V₁
V₁ = ∫π×y²×dx (1)
Now
( x - r/2)² + y² = r² the equation of circumference 1
y² = r² - ( x - r/2)²
Plugging this value in equation (1)
V₁ = ∫π×[ r² - ( x - r/2)²]×dx with integrations limits 0 ≤ x ≤ r/2
V₁ = π×∫ ( r² - x² + (r/2)² - r×x )×dx
V₁ = π× [ r²×x - x³/3 + (r/2)²×x - (1/2) × r × x²] evaluate between 0 and r/2
V₁ = π× [(5/4)×r²×x - x³/3 - (1/2) × r × x²]
V₁ = π× [(5/4)×r² × ( r/2 - 0 ) - (1/3)×(r/2)³ - (1/2) × r × (r/2)²]
V₁ = π× [ (5/8)×r³ - r³/24 - r³/8]
V₁ = π× (11/24)×r³
Then
V = 2× V₁
V = 2×π×11/24)×r³
V = (11/12)×π×r³
To know more about volume, here
https://brainly.com/question/22907480
#SPJ4

One angle of an isosceles triangle measures 112°. What measures are possible for the
other two angles? Choose all that apply.
30°
35°
760
340
Answers
Answer:
34°
Step-by-step explanation:
A triangle measures 180°
An isosceles triangle has two angles and sides with equal measurements.
We know that one angle is 112°. Thus, we can use that to form an equation to solve for the unknown values:
112° + x + x = 180°
112° + 2x = 180°
2x = 68
x = 34°
The other two angles each measure 34°.
Check:
112 + 34 + 34 = 180
hope this helps and is right!! p.s. i really need brainliest :)
Answer:
34°
Step-by-step explanation:
Sum of interior angles of a triangle is 180°
Two of the interior angles of an Isosceles triangle are equal
Given one of the interior angles is 112° then the remaining two angle must be equal:
⇒ 112 + 2x = 180
⇒ 2x = 68
⇒ x = 34°
a play starts at 7:30pm, first act last 46 minutes, interval lasts 20 minutes. second act lasts 53 minutes, what time does the second act end?
Answers
Answer:
9:thirty one
Step-by-step explanation:
Add 46 twenty and 5three then add the answer in 7:thirty
The graph shows how the length of time a stroller is rented at an amusement park is related to the rental cost. what is the rate of change shown in the graph?

Answers
Each time the number of hours (on the x axis) goes up by 1, the cost (on the y axis) goes up by up by $2. So each hour costs $2.
You can pick two points on the graph, such as (1,2) and (2,4) to compute the slope using the slope formula below
m = (y2 - y1)/(x2 - x1)
m = (4-2)/(2-1)
m = 2/1
m = 2 we get a slope of 2
The slope is the rise/run
rise = change in cost = change in y
run = change in time = change in x
The sum of the first 9 term is 171 and the sum of the next 5 term is 235 find the common difference,first term and sequence
Answers
The arithmetic sequence is:
3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43,....
Common difference = 4
First term = 3
How to find the sum of an arithmetic sequence?The formula for the sum of the first n terms of an arithmetic sequence is:
Sₙ = ⁿ/₂[2a + (n − 1)d]
where:
n = the number of terms to be added.
a = the first term in the sequence.
d = common difference
We are told that sum of the first 9 term is 171. Thus:
(9/2) [2a + (9 − 1)d] = 171
(2a + 8d) = 38 ----(1)
Sum of the next 5 term is 235.
Thus, sum of the first 14 terms = 235 + 171 = 406
(14/2) [2a + (14 − 1)d] = 406
7(2a + 13d) = 406
2a + 13d = 58 -----(2)
Subtract eq 1 from eq 2 to get:
5d = 20
d = 4
2a + 13(4) = 58
2a = 58 - 52
a = 3
Sequence is:
3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43,....
Read more about Sum of arithmetic sequence at: https://brainly.com/question/28369191
#SPJ1
Find the point where the line intersects the plane:
Line: x = -1 , y = 1 + t , z = 1 + 2t ; Plane x + y + z = 13
Answers
The point where the line intersects the plane is (-1, 7, 13).
To find the point where the line intersects the plane, we need to substitute the equations of the line into the equation of the plane and solve for the parameter t.
Substituting x, y, and z from the equation of the line into the equation of the plane, we get:
x + y + z = 13
(-1) + (1 + t) + (1 + 2t) = 13
2t + 1 = 13
2t = 12
t = 6
Now we can substitute t = 6 back into the equations of the line to find the point of intersection:
x = -1
y = 1 + t = 1 + 6 = 7
z = 1 + 2t = 1 + 2(6) = 13.
For more similar questions on plane:
https://brainly.com/question/1655368
#SPJ11
The bakery made 110 pumpkin muffins. They will be packed
in boxes with 8 muffins in each box. About how many boxes
will there be?
Answers
Answer:
118
Step-by-step explanation:
you should have learned this in 1st grade
Answer: 14 boxes
Step-by-step explanation:
Divide 110 by 8 and you get 13.75. You will then round up to the nearest hole number to make sure that almost all the boxes have 8 muffins in each.
Which expression is equivalent to (x^6y^8)^3 / x^2y^2?
Answers
Answer:
=x^16y^26
Step-by-step explanation:
x^18y^24xy^2
x^16y^24xy^2
Answer:
D (x^16y^22)
Step-by-step explanation:
For edge
On Map 1, which has a scale of 1:25000, length of road is 5.5cm and the area of a park is 1.4cm2
On Map 2, which has a scale of 1: n, the area of the same park is 35 cm2.
Find the value of n.
Answers
Answer:
50 km
Step-by-step explanation:
So the map has a scale of 1 cm: 20 km. Next, you look at how far they are apart and see if the scale and the distance on the map are the same measurement. In this case, they are both centimeters so they stay the same. Then, all you do is multiple the real size, 20 km, by
2.5
1
. Then, 20 x 2.5=50. So the answer is 50 km
A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 35% salt and Solution B is 60% salt. She wants to obtain 50 ounces of a mixture that is 55% salt. How many ounces of each solution should she use?
Answers
Answer:
Step-by-step explanation:From the issue, we may deduce that:
x + y = 50 She desires to produce 50 ounces of the combination (because to this).
(0.35x) + (0.60y) = 0.55(x+y) (because we're calculating the amount of salt in each solution and the combination contains 55% salt)
We may take the first equation and replace it in the second equation:
(0.35x) + (0.60y) = 0.55(50) (50)
0.35x + 0.60y = 27.5 when x is substituted.
A system of two equations with two variables is now available:
x + y = 50\s0.35x + 0.60y = 27.5
To determine one of the variables in terms of the other, we may utilize the first equation. Let's figure out y:
y = 50 - x
We now change y in the second equation to the following expression:
0.35x + 0.60(50-x) = 27.5
Finding the value of x:
0.35x + 30 - 0.6x = 27.5
0.25x= -2.5
x= -10
Since the number of ounces cannot be negative, the answer is illogical. As a result, you should double-check your calculations or determine if the issue statement contains a mistake.
To get the answer, you can also try an alternative approach like substitution or elimination. Then, double-check your calculations.
The scatter plot below shows nine points from a data set. 12.0 10.8 9.6 8.4 7.2 6.0 4.8 3.6 2.4 1.2 ● 0 1 2 3 4 5 6 7 8 9 10
A 4,4,5,5,6,6
b 4,10,4,11,4,12
C8,9,8,10,8,11
D10,10,10,11,10,12
Answers
Answer:
Therefore, based on the given scatter plot, the set of numbers that matches the points is C. 8,9,8,10,8,11.
Step-by-step explanation:
The scatter plot shown represents a set of nine points on a coordinate plane. Each point consists of an x-coordinate and a y-coordinate. To determine which set of numbers corresponds to the scatter plot, we need to analyze the pattern in the given points.
Looking at the scatter plot, we observe that the x-coordinates range from 0 to 10 with an increment of 1, while the y-coordinates seem to vary.
Now let's examine the given answer choices:
A. .4,4,5,5,6,6
B. .4,10,4,11,4,12
C. 8,9,8,10,8,11
D. 10,10,10,11,10,12
Set C (8,9,8,10,8,11) among these answer choices matches the pattern observed in the scatter plot. The x-coordinates in the scatter plot range from 0 to 10, and the y-coordinates correspond to the numbers provided in set C.
Therefore, based on the given scatter plot, the set of numbers that matches the points is C.
For more questions on this topic refer to this link:
https://brainly.com/question/6592115
#SPJ8
You are given a 4-sided die with each of its four sides showing a different number of dots from 1 to 4. When rolled, we assume that each value is equally likely. Suppose that you roll the die twice in a row. (a) Specify the underlying probability space (12,F,P) in order to describe the corresponding random experiment (make sure that the two rolls are independent!). (b) Specify two independent random variables X1 and X2 (Show that they are actually inde- pendent!) Let X represent the maximum value from the two rolls. (c) Specify X as random variable defined on the sample space 1 onto a properly determined state space Sx CR. (d) Compute the probability mass function px of X. (e) Compute the cumulative distribution function Fx of X.
Answers
(a) Ω = {1, 2, 3, 4} × {1, 2, 3, 4}, F = power set of Ω, P assigns equal probability (1/16) to each outcome.
(b) X1 and X2 represent the values of the first and second rolls, respectively.
(c) X is the random variable defined as the maximum value from the two rolls, with state space Sx = {1, 2, 3, 4}.
(d) pX(1) = 1/16, pX(2) = 3/16, pX(3) = 5/16, pX(4) = 7/16.
(e) The cumulative distribution function Fx of X:
Fx(1) = 1/16, Fx(2) = 1/4, Fx(3) = 9/16, Fx(4) = 1.
(a) The underlying probability space (Ω, F, P) for the random experiment can be specified as follows:
- Sample space Ω: {1, 2, 3, 4} × {1, 2, 3, 4} (all possible outcomes of the two rolls)
- Event space F: The set of all possible subsets of Ω (power set of Ω), representing all possible events
- Probability measure P: Assumes each outcome in Ω is equally likely, so P assigns equal probability to each outcome.
Since the two rolls are assumed to be independent, the joint probability of any two outcomes is the product of their individual probabilities. Therefore, P({i} × {j}) = P({i}) × P({j}) = 1/16 for all i, j ∈ {1, 2, 3, 4}.
(b) Two independent random variables X1 and X2 can be defined as follows:
- X1: The value of the first roll
- X2: The value of the second roll
These random variables are independent because the outcome of the first roll does not affect the outcome of the second roll.
(c) The random variable X can be defined as follows:
- X: The maximum value from the two rolls, i.e., X = max(X1, X2)
The state space Sx for X can be determined as Sx = {1, 2, 3, 4} (the maximum value can range from 1 to 4).
(d) The probability mass function px of X can be computed as follows:
- pX(1) = P(X = 1) = P(X1 = 1 and X2 = 1) = 1/16
- pX(2) = P(X = 2) = P(X1 = 2 and X2 = 2) + P(X1 = 2 and X2 = 1) + P(X1 = 1 and X2 = 2) = 1/16 + 1/16 + 1/16 = 3/16
- pX(3) = P(X = 3) = P(X1 = 3 and X2 = 3) + P(X1 = 3 and X2 = 1) + P(X1 = 1 and X2 = 3) + P(X1 = 3 and X2 = 2) + P(X1 = 2 and X2 = 3) = 1/16 + 1/16 + 1/16 + 1/16 + 1/16 = 5/16
- pX(4) = P(X = 4) = P(X1 = 4 and X2 = 4) + P(X1 = 4 and X2 = 1) + P(X1 = 1 and X2 = 4) + P(X1 = 4 and X2 = 2) + P(X1 = 2 and X2 = 4) + P(X1 = 3 and X2 = 4) + P(X1 = 4 and X2 = 3) = 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 = 7/16
(e) The cumulative distribution function Fx of X can be computed as follows:
- Fx(1) = P(X ≤ 1) = pX(1) = 1/16
- Fx(2) = P(X ≤ 2) = pX(1) + pX(2) = 1/16 + 3/16 = 4/16 = 1/4
- Fx(3) = P(X ≤ 3) = pX(1) + pX(2) + pX(3) = 1/16 + 3/16 + 5/16 = 9/16
- Fx(4) = P(X ≤ 4) = pX(1) + pX(2) + pX(3) + pX(4) = 1/16 + 3/16 + 5/16 + 7/16 = 16/16 = 1
To know more about probability, refer here:
https://brainly.com/question/28259612
#SPJ4
Use the image to answer the question.Identify the legs in AXYZ.
Answers
Answer
option C
Explanation:
Given the right angled triangle XYZ
The legs are Length YZ and Length ZX
Therefore, the legs are YZ AND ZX

g do you think that the model suffers from omitted variable bias and the estimate for age is unbiased? explain.
Answers
When a crucial variable is excluded from a regression model, the results are referred to as omitted variable bias.
Regression analysis frequently encounters the issue of omitted variable bias, which occurs when an important independent variable is left out of the model and affects the estimates of the coefficients for the included variables.
This happens because one or more of the included independent variables as well as the dependent variable may be correlated with the variable that was left out. As a result, the intercept and coefficients of the included independent variables may be overestimated or underestimated.
Based on prior knowledge and theory, researchers should carefully consider which variables to include in the model to address this issue. They should then test for potential correlations between the included and
Learn more about omitted variable bias:
https://brainly.com/question/26424928
#SPJ4
