Pls help me!!!!!!!!!!!!!!!

The simplified form of the expression 1/5 divied by 2 as a fraction is 1/10.

Given the expression in the question;

1/5 divied by 2

1/5 ÷ 2

To simplify, multiply 1/2 by the reciprocal of 2

1/5 ÷ 2

1/5 × 1/2

Simplify

( 1 × 1 ) / ( 5 × 2 )

( 1 ) / ( 5 × 2 )

Multiply 5 and 2

( 1 ) / ( 10 )

1/10

Therefore, the simplified form is 1/10.

Learn more about fractions heres; https://brainly.com/question/10354322

#SPJ1

Answer:

Step-by-step explanation:

J

The length of the smallest part of the line segment is 12 cm.

The line segment of length 96 cm is divided into 3 parts with the ratio of 2:9:5. The given ratio is a part-to-whole ratio. We can find the lengths of the parts by applying the formula:

Part = Whole × Ratio

Part 1 = 96 cm × (2/16)

= 12 cm

Part 2 = 96 cm × (9/16)

= 54 cm

Part 3 = 96 cm × (5/16)

= 30 cm

Therefore, the length of the smallest part of the line segment is 12 cm.

Learn more about line segment here:

https://brainly.com/question/30072605

#SPJ4

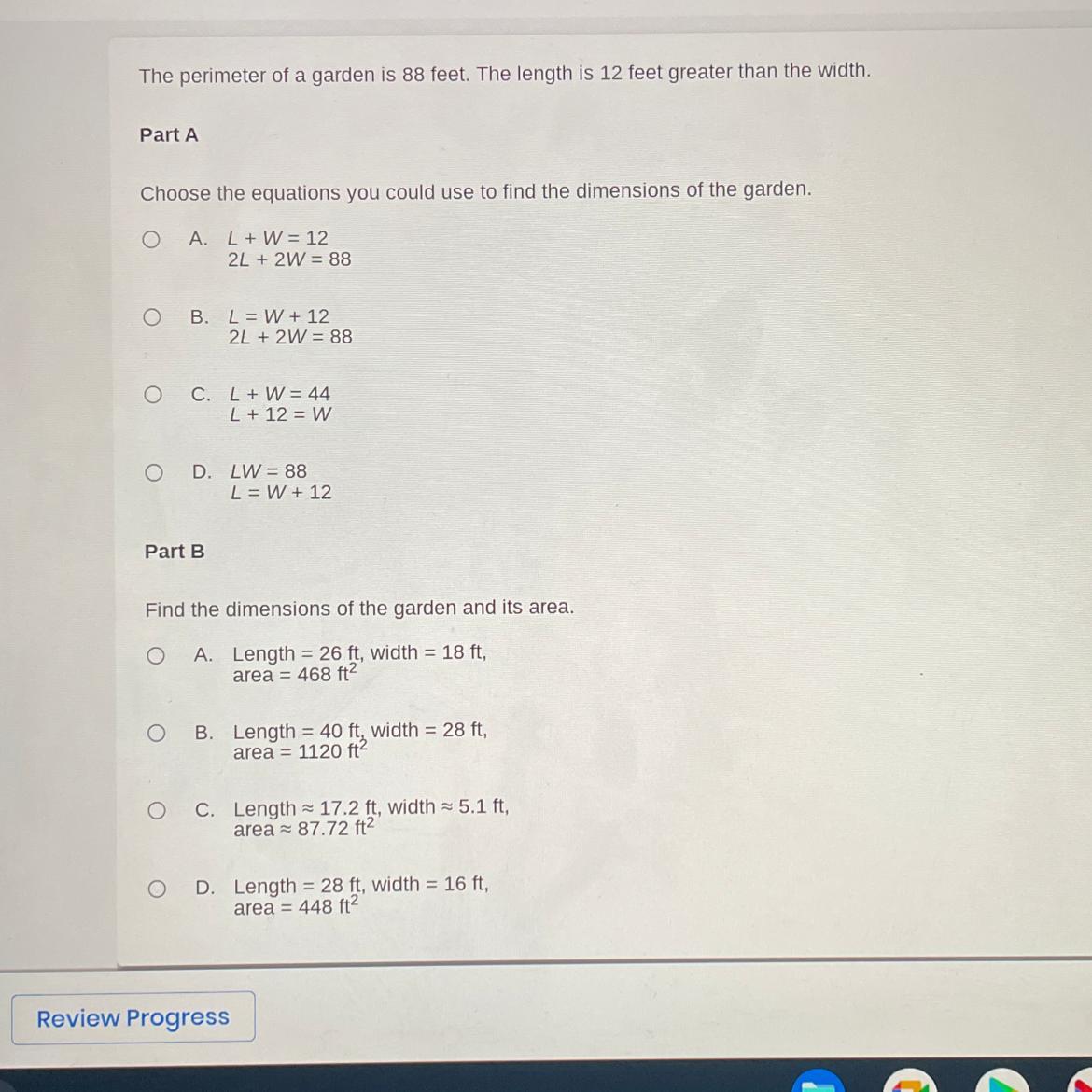
Answer:

Step-by-step explanation:

A. L+W= 2 in. x 2 in. = 4 in.

Below are some things to help you with perimeter and area(just type it into whatever browser you use, copy and paste)

https://youtu.be/LoaBd-sPzkU

https://th.bing.com/th/id/OIP.Q5D_8qbK_9XGQLj1s0tpbwHaJ3?w=186&h=248&c=7&r=0&o=5&dpr=1.65&pid=1.7

A trinomial is a polynomial with three terms that has a leading coefficient of 3 and a constant term of -5 is

3m²+m-5

Here the degree of the trinomial is 2, so the leading coefficient is the coefficient of the term with m², which is 3.

The constant term is the term without a variable, which is -5

To find the coefficient of middle term of the trinomial, formula is:

coefficient of middle term =

(sum of the coefficients of the first and last terms)

                                    2

The sum of the coefficients of the first and last terms is 3 - 5 = -2.

Dividing by 2, we get -1 as the coefficient of the middle term.

Putting all of this together, we can write the trinomial as:                     3m² +m - 5

Learn  more about polynomials here:

https://brainly.com/question/11536910

#SPJ11

The radius of the curved path of the car such that it is not skidding is 51.2 meters.

A car is moving in a curved path at constant speed. By Newton's laws and equation of friction, we find that the square of the car's speed (v), in meters per second, is directly proportional to the radius of the curve path (s) and to the coefficient of friction (μ), no unit:

v² = k · R · μ

Where k is the constant of proportionality.

If we know that R = 40 m, v = 4√10 m / s, μ = 0.4, v' = 10 m / s, μ' = 0.5, then the resulting radius is:

v'² / (μ' · R') = v² / (μ · R)

10² / (0.4 · 40) = (4√10)² / (0.5 · R)

0.5 · R = (4√10)² · (0.4 · 40) / 10²

0.5 · R = 128 / 5

R = 256 / 5

R = 51.2 m

The radius of the curved path is 51.2 meters.

To learn more on direct relationships: https://brainly.com/question/14580439

#SPJ1

Answer:

143 oil changes

Step-by-step explanation:

We first find the unit rate.

(91 oil changes)/(7 days) = 13 oil changes/day

Since we want to know the number of oil changes in 11 days, we multiply the unit rate by 11 days.

13 oil changes/day * 11 days = 143 oil changes

The given problem concerns a vibrating circular drumhead fixed along the circumference. The following problem needs to be solved for the two-dimensional wave equation to find the displacement for all positive time.

The Bessel functions of the first kind are solutions of the Bessel differential equation, which is the second-order linear ordinary differential equation. The solutions of the Bessel differential equation are periodic, meaning that they repeat themselves after a fixed interval.

A problem was given to determine the displacement of a vibrating circular drumhead fixed along the circumference. The following problem has to be solved for the two-dimensional wave equation 1,0,t)0, a(r, θ, 0) = 1-r2, udT.0, 0) = 1, linn la(r, θ, t)| < oo where (r, ) are polar coordinates on a circle, and V2 denotes the Laplacian in Cartesian coordinates (x, y).

A Fourier-Bessel series was also given.n= where kn is the n-th positive zero of the Bessel function Jo.

To find the displacement of a vibrating circular drumhead fixed along the circumference, the following problem has to be solved for the two-dimensional wave equation.1,0,t)0, a(r, θ, 0) = 1-r2, udT.0, 0) = 1, linn la(r, θ, t)| < oo where (r, ) are polar coordinates on a circle, and V2 denotes the Laplacian in Cartesian coordinates (x, y).The Bessel functions of the first kind are solutions of the Bessel differential equation, which is the second-order linear ordinary differential equation. The solutions of the Bessel differential equation are periodic, meaning that they repeat themselves after a fixed interval.

A Fourier-Bessel series was given by n= where kn is the n-th positive zero of the Bessel function Jo. The Fourier-Bessel series of the problem is given by u(r,θ,t) =  ∑an(t)J0(knr)J0(kn).The problem requires the initial displacement of the drumhead to be radially symmetric along the circle with the maximum displacement taken at the center.

The initial velocity is a positive constant.To solve the given problem for the two-dimensional wave equation, we can use the separation of variables method to separate the solution of the equation into a product of functions of r and θ and a function of t. The general solution of the given problem for the two-dimensional wave equation is given byu

(r, θ, t) =  ∑an(t)J0(knr)J0(kn).

Therefore, we can conclude that to find the displacement of a vibrating circular drumhead fixed along the circumference, the following problem has to be solved for the two-dimensional wave equation. The general solution of the given problem for the two-dimensional wave equation is given by u(r, θ, t) =  ∑an(t)J0(knr)J0(kn).

To know more about Fourier-Bessel series :

brainly.com/question/31046635

#SPJ11

Answer:

Answer is B ( 314.9 m2)

Step-by-step explanation:

A= H(B)/2

A= 25.6(24.6)/2

A= 314.88

Answer:

7.625597485 DFNFNFJFKJFKF

Answer:

√3

√5

22/7.

16/4

Step-by-step explanation:

22/7 = 3.14

√3 = 1,73

16/4 = 4

√5 = 2.23

the least would have the smallest value. the greatest would have the largest value

This is a simple inequality problem involving absolute values.

The given inequality is: $-4 < |x-3|$.We need to find the range of real values of $x$ that satisfy this inequality.
First, let's consider the case when $x-3$ is positive. In this case, the absolute value of $x-3$ is simply $x-3$. So, we can write the inequality as: $-4 < x-3$
Adding $3$ to both sides, we get: $-1 < x$

This means that all values of $x$ greater than $-1$ satisfy the inequality when $x-3$ is positive.
Now, let's consider the case when $x-3$ is negative. In this case, the absolute value of $x-3$ is $-(x-3)$. So, we can write the inequality as: $-4 < -(x-3)$. Expanding the right-hand side, we get: $-4 < -x + 3$

Subtracting $3$ from both sides, we get: $-7 < -x$. Multiplying both sides by $-1$ (which reverses the inequality), we get: $x < 7$.This means that all values of $x$ less than $7$ satisfy the inequality when $x-3$ is negative. Putting both cases together, we have:$x < 7$ or $x > -1$
This is the final answer. We can express it more concisely as:
$-1 < x < 7$

To know more about inequality visit:

https://brainly.com/question/30297652

#SPJ11

Answer:

So, the step1 is correct.

Step-by-step explanation:

The expression is

\((6 x^3 + 8 x^2 - 7 x)-(2x^2 + 3)(x- 8)\\\\(6 x^3 + 8 x^2 - 7 x) - (2x^3 - 16 x^2 + 3 x - 24)\\\\6 x^3 + 8 x^2 - 7 x - 2 x^3 - 16 x^2 + 3 x - 24\\\\4 x^3 - 8 x^2 - 4 x - 24\)

So, the step 1 is correct.

Answer:

16

Step-by-step explanation:

\(\sqrt{121}\) + \(\sqrt[3]{125}\)

= 11 + 5

= 16

Answer:

7

Step-by-step explanation:

(f + g)(n) = f(n) + g(n) = n - 3 + n - 2 = 2n - 5 , thus

(f + g)(6) = 2(6) - 5 = 12 - 5 = 7

Answer:

nine below zero

nine less than zero

the opposite of 9

Step-by-step explanation:

(brainliest plz)

Answer:

I hope this helps!

Answer:

domain is all real numbers

To determine the required sample size for a political poll with a 4% margin of error and a 97.5% confidence level, a formula can be used. For this scenario, the sample size required would be approximately 862 respondents.

To calculate the sample size needed for a political poll with a 4% margin of error and a 97.5% confidence level, the following formula can be used:

n = (Z^2 * p * (1-p)) / E^2

Where:

n is the sample size

Z is the Z-score associated with the desired confidence level (in this case, it is 2.24)

p is the expected proportion of support for the candidate (this value is typically unknown, so a conservative estimate of 0.5 is often used to get the maximum sample size)

E is the margin of error

Plugging in the values for this scenario, we get:

n = (2.24^2 * 0.5 * (1-0.5)) / 0.04^2

n ≈ 862

Therefore, the required sample size for this political poll is approximately 862 respondents. This sample size would provide a margin of error of 4% at a 97.5% confidence level, meaning that there is a 97.5% chance that the true proportion of support for the candidate lies within the range of the survey results plus or minus the margin of error.

Learn more about Sample Size:

brainly.com/question/25894237

#SPJ11

The center and the radius by completing the square of the given equation of circle is x² + y² - 32x+24y +396 = 0 is C( -16, 12) and radius is 2.

The equation of the circle is given as x² + y² - 32x+24y +396 = 0.

Comparing the given equation with general equation of circle, x² + y² + 2gx + 2fy + c = 0.

The center of circle is C = (-g, -f)

The radius of circle is r = √g² + f² - c

Therefore, from the given equation,

2g = -32

g = -16

2f = 24

f = 12

C( -16, 12)

And the radius is

r = √(-16)² + (12)² - 396

= √256 + 144 -396

=√4

= 2

Hence, the center and the radius by completing the square of the given equation of circle is x² + y² - 32x+24y +396 = 0 is C( -16, 12) and radius is 2.

To know more about circle check the below link:

https://brainly.com/question/14150470

#SPJ1

a) 28.15 min

b) Yes, it is possible to ingest more food energy than one can burn via exercise.

Given,

Energy in a cup of Yoghurt = 929KJ (222Kcal) = 929000 J

Rate at which the woman is doing work=110W

Efficiency of women working = 20.0%

We know,

Power = Energy /Time

∴Time=Energy /Power

⇒Time= 929000 / 110

⇒Time=8445.45 sec

Since, the efficiency with which the women is working is 20%

∴Time= 20 ×8445.45 / 100 =1689.09 sec

∴Time in minutes = 1689.09 /60 min

                               =28.15 minutes

(b)Food contains a lot of energy, which exercise only slowly expends. Yes, it is possible to ingest more food energy than one can burn via exercise.

To know more about efficiency refer to:

brainly.com/question/13021831

#SPJ4

The new equation that will be formed is x − 3(6x − 1) = −11 (third option).

The substitution method is one of the methods that is used to solve simultaneous equations. It entails making one of the variables subject of the formula and substituting for it in the second equation.  Other methods that can be used to solve simultaneous equations are the graph method and the elimination method.

The two simultaneous equations given are:

6x − y = 1 equation 1

4x − 3y = −11 equation 2

When y in equation 1 is made subject of the formula, the equation formed is:

y = 6x - 1 equation 3

Substitute for y in equation 2

4x - 3(6x - 1) = -11

To learn more about simultaneous equations, please check: https://brainly.com/question/25875552

#SPJ1

1. The equation of the straight line is y = -x -1.

2. The equation of the point-gradient form is 3x -y - 10.

3. The equation of the straight line that is parallel to the line y = x-2 and goes through the point (0,1) is y = x + 1.

What is a straight line?

A line is an object in geometry that is indefinitely long and has neither breadth nor depth nor curvature. Since lines can exist in two, three, or higher-dimensional environments, they are one-dimensional things. In daily language, a line segment with two points designating its endpoints is also referred to as a "line."

Here, we have

1. The slope-intercept form of the equation of a line is:

y = mx + b

We are fortunate to be given the y-intercept, the point(0,-1) therefore, the value, b, in the slope-intercept form is -1:

y = mx - 1

Substitute the other point(-1,0) into the equation and then solve for the value of m:

0 = -m - 1

m = -1

y = -x -1

Hence, the equation of the straight line is y = -x -1.

2. We know that the equation of a line passing through the point (x₀, y₀  ) whose slope is m is (y -  y₀) = m(x -x₀)

The equation of a line passing through the point(2,-4) and the slope is 3.

(y+4) = 3(x-2)

y + 4 = 3x - 6

3x -y - 10

Hence, the equation of the point-gradient form is 3x -y - 10.

3. Consider the given equation: y = x-2

Since, the line is parallel to given line. so slope will be same.

slope = 1

We know that the second line will also have a slope of 1, and we are given the point (0,1). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.

y = mx + b

1 = b

Now, we put the value of b in the equation and we get

y = x + 1

Hence, the equation of the straight line that is parallel to the line y = x-2 and goes through the point (0,1) is y = x + 1.

To learn more about the straight line from the given link

https://brainly.com/question/25969846

#SPJ1

Step-by-step explanation:

Since Shanika is standing near the pole, we can safely assume that the triangle formed by Shanika and her shadow is a smaller version of the triangle formed by the pole and its shadow.

By similar triangles:

\( \frac{x \: of \: pole}{y \: of \: pole} = \frac{x \: of \: shanika}{y \: of \: shanika} \\ \frac{16}{ height \: of \: pole} = \frac{4}{5} \\ 16(5) = 4 \times height \: of \: pole \\ height \: of \: pole = \frac{80}{4} \\ = 20\)

The height of the pole is 20ft.

Answer:

The sum of interior angle =180

given;

3x +3x +4x =180

    10x = 180

  x =180/10

x =18

so put the value of  x =18  in 3x, 3x and 4x

   = 3x

   =3 ×18

   = 54

   2nd one   = 4 x

                 = 4×18

                  = 72

All three angles are 54,54,72

Step-by-step explanation:

The angle measures of the triangle are 54°, 54° and 72°.

Ratio is simply a relationship between two or more numbers, quantity or size of objects.

If 'a' is related to 'b', then their ratio is denoted by a : b.

Let A, B and C be the three angles of this triangle.

Ratio of interior angles of the triangle, A : B : C = 3 : 3 : 4

Then angle A = 3x, B = 3x and C = 4x, by the definition of ratio.

Also, we know sum of the interior angles of a triangle = 180°

⇒ 3x + 3x + 4x = 180

⇒ 10x = 180

⇒ x = 180 / 10

⇒ x = 18

Therefore,

A = 3x = 3 × 18 = 54

B = 3x = 3 × 18 = 54

C = 4x = 4 × 18 = 72

Hence the measures of the angles of the triangle whose angles are in the ratio 3 : 3 : 4 are  54°, 54° and 72°.

To learn more about Ratio, click :

https://brainly.com/question/1504221

#SPJ2

Answer:

\(x=6\\y=12\)

Step-by-step explanation:

To find the value of x you can use sin rule

\(sin(60)=\frac{oppoaite}{hypotenuse}\\\frac{\sqrt{3} }{2} =\frac{x}{4\sqrt{3} } \\\)

Use cross multiplication

\(4*\sqrt{3} *\sqrt{3} =2x\\4*3=2x\\12=2x\\\frac{12}{2} =\frac{2x}{2} \\6 =x\)

To find the value of y you have to use sin rule again

\(sin(30)=\frac{opposite}{hypotenuse}\\\frac{1}{2} =\frac{x}{y} \\\frac{1}{2} =\frac{6}{y} \\\)

Use cross multiplication

\(y=6*2\\y=12\)

Hope this helps you.

Let me know if you have any other questions :-)

Given that Kenyon ran for 8 miles each week while training. And, here is his record of the number of miles he ran.

Monday: 2 miles

Tuesday: x miles

Wednesday: 6 miles

Thursday: x + 0.4 miles

Friday: 2 miles.

He ran a total of 8 miles this week i.e.2 + x + 6 + x + 0.4 + 2 = 8

Simplifying this, we get, x = 0.6

Hence, Kenyon ran 0.6 miles on Tuesday and 1 mile (0.6 + 0.4) on Thursday. The main answer is Kenyon ran 0.6 miles on Tuesday and 1 mile (0.6 + 0.4) on Thursday.

Given, Kenyon ran 8 miles each week while training and it is given that he ran 2 miles on Monday and 6 miles on Wednesday. He ran x miles on Tuesday and (x + 0.4) miles on Thursday.Now, the total number of miles ran by Kenyon this week is 8 miles.

Hence, we can write the equation as:2 + x + 6 + (x + 0.4) + 2 = 8

Simplifying the above equation, we get2x + 0.4 = 0.4x = 0.6

Therefore, the number of miles Kenyon ran on Tuesday is 0.6 miles.And, the number of miles he ran on Thursday is (0.6 + 0.4) miles = 1 mile.

Therefore, Kenyon ran 0.6 miles on Tuesday and 1 mile (0.6 + 0.4) on Thursday.

To know more about miles visit:

brainly.com/question/12665145

#SPJ11