Answers
Related Questions
A store stocked 180 cans of popcorn for a weekend sale. During the weekend, 63 of the cans sold. What percent of the cans of popcorn stocked were sold that weekend?
Answers
Answer:
35%
Step-by-step explanation:
So 63 out of 180 cans were sold. Write that as a fraction (63/180) and then convert that to a decimal by finding the quotient of 63 and 180 and convert the resulting decimal into a percent.
The solution of the equation 3x + 4 =1 is a) 1 b) 0 c) -1 d) 2
Answers
Hello!
3x + 4 = 1
3x + 4 - 4 = 1 - 4
3x = -3
3x/3 = -3/3
x = -1
The solution of the equation 3x + 4 = 1 is -1.
The answer is:
C) x = -1
Work/explanation:
To solve this equation, I subtract 4 from each side:
\(\sf{3x+4=1}\)
Subtract :
\(\sf{3x=-3}\)
Divide each side by 3:
\(\sf{x=-1}\)
Hence, C is correct.
Which angle number represents SXU?

Answers
Answer:
Angle 2
Step-by-step explanation:
Find S and find X.
Then find U.
The angle at X connected to S and U is the angle number.
10. y=x² - 4x - 5
D =
R =
Function?
Answers
From the given expression, the factors are x+1 and x - 5 and the zeros of the function is equivalent to -1 and 5
How to factorize a function?Factorisation is defined as the breaking or decomposition of an entity. Given the quadratic equation below;
y=x² - 4x - 5
Factorize
y = x^2 - 5x + x - 5
y = x(x - 5) + 1(x - 5)
y = (x+1)(x-5)
From the given expression, the factors are x+1 and x - 5 and the zeros of the function is equivalent to -1 and 5
Learn more on factorization here: https://brainly.com/question/25829061
#SPJ1
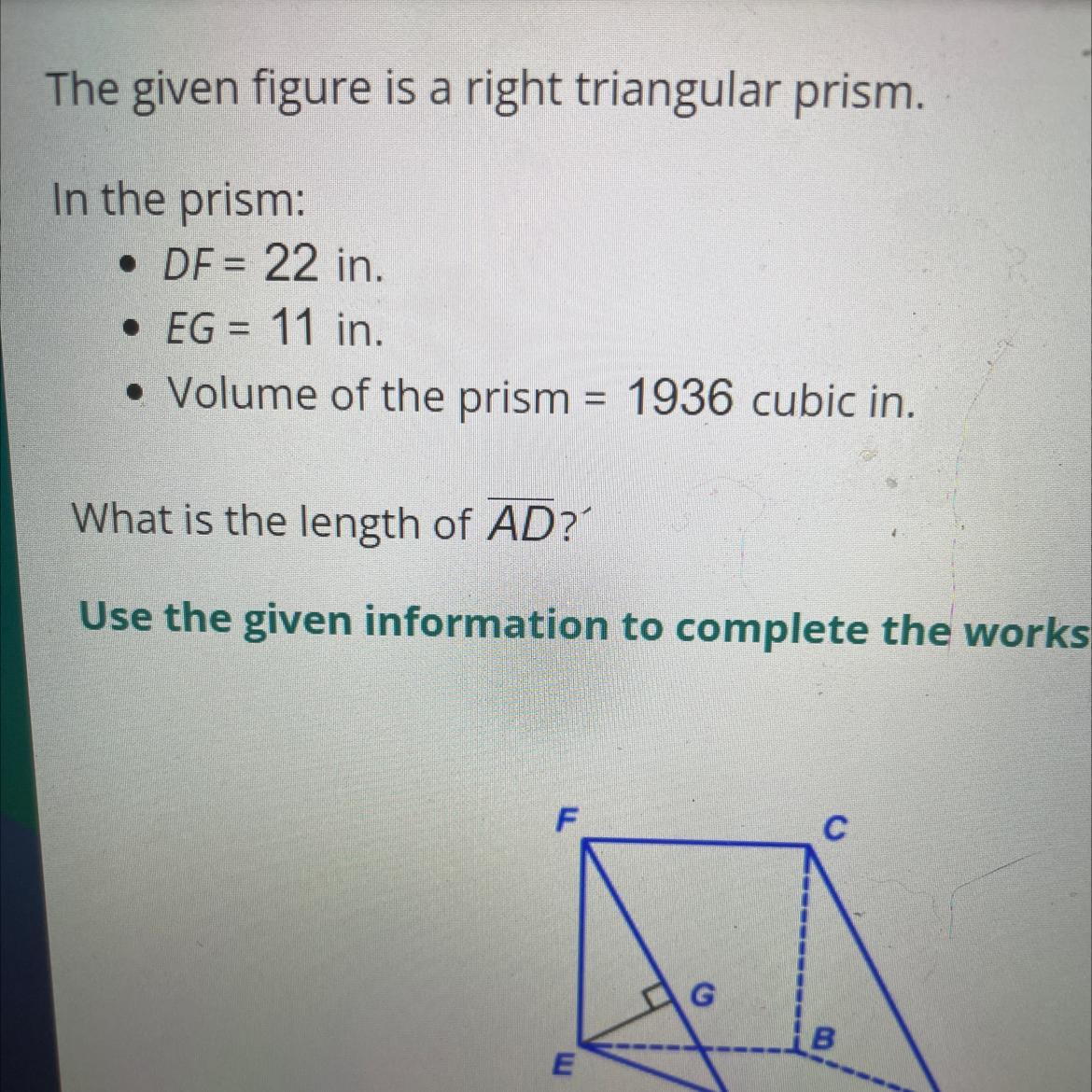
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Central High School plays Eastern High School in a basketball game. Eastern had double the score of Central before Central scored a three-pointer as the game ended.
The variable, c, represents Central's score before the three-pointer. Express the total points scored in the game as a variable expression. Check all that apply.
2c + c
3c + 3
2c + 3
2c + c – 3
2c – c + 3
2c + c + 3
Answers
At a popular rock-climbing site in Yosemite National Park, a randomly selected
Answers
Answer:
please be more specific
Step-by-step explanation:
Select all values that satisfies the inequality 2f >–8
options-
4
4
0
-6
3.5
-2.25
-100
Answers
Step-by-step explanation:
2f > -8
f > -4
The values greater than -4 here are 4, 0, 3.5 and -2.25.
solve 6x²-42=0 with the exact values of x
Answers
Answer:
X=-√7 and √7
Step-by-step explanation:
To solve the equation 6x² - 42 = 0, we can begin by rearranging it to isolate the variable term:
6x² = 42
Then, we can divide both sides by 6:
x² = 7
To get the exact values of x, we need to take the square root of both sides:
x = ±√7
Therefore, the exact values of x are √7 and -√7.
The original plan for assigning telephone numbers that you investigated in
Applications Task 4 was implemented in
1947. At that time, the supply of numbers was expected to last for 300 years. However, by the 1970s the numbers were already starting to run out. So, the numbering plan
had to be modified. In this task, you will count the number of different phone numbers that were available in 2012.
a. For three-digit area codes, the first digit cannot be a 0 or a 1. Assuming no additional restrictions, how many three-digit area codes are possible under
this plan?
b. Certain area codes are classified as "Easily Recognizable Codes" (BRCs).
ERCs designate special services, like 888 for toll-free calls. The requirement for an ERC is that the second and third digit of the area code must be the same. The first digit again cannot be a 0 or a 1. How many ERCs are there?
c. Consider the seven digits after the area code. As with the area code, the first digit of the three-digit local prefix cannot be a 0 or a 1. The remaining six digits for the local number have no restrictions. How many of these seven-digit phone numbers are possible?
d. Assuming only the 0 and 1 restrictions in Parts a and c, how many ten-digit phone numbers are possible?
Answers
a. Assuming no additional restrictions, there are 800 possible three-digit area codes.
b. Considering ERCs, there are 80 ERCs.
c. For the seven digits after the area code, there are \(8 \times 10^6 = 8,000,000\) possible seven-digit phone numbers.
d. Assuming only the 0 and 1 restrictions from parts a and c, the number of possible ten-digit phone numbers is 800 \(\times\) 8,000,000 = 6,400,000,000.
a. For three-digit area codes, the first digit cannot be 0 or 1.
Assuming no additional restrictions, there are 8 possibilities for the first digit (2-9) and 10 possibilities for each of the remaining two digits (0-9). Therefore, the total number of three-digit area codes possible under this plan is \(8 \times 10 \times 10 = 800.\)
b. For an ERC (Easily Recognizable Code), the second and third digits of the area code must be the same, and the first digit cannot be 0 or 1. There are 8 possibilities for the first digit (2-9) and 10 possibilities for the third digit (0-9).
Since the second digit must be the same as the third digit, there is only 1 possibility.
Therefore, the total number of ERCs is \(8 \times 1 \times 10 = 80.\)
c. For the seven digits after the area code, the first digit of the three-digit local prefix cannot be 0 or 1.
There are 8 possibilities for the first digit (2-9) and 10 possibilities for each of the remaining six digits (0-9).
Therefore, the total number of seven-digit phone numbers possible is 8 * \(10\times 10 \times 10 \times 10 \times 10 \times 10 = 8,000,000.\)
d. Assuming only the 0 and 1 restrictions from parts a and c, the number of possible ten-digit phone numbers can be calculated by multiplying the number of possibilities for each digit position.
For the area code (part a), there are 800 possibilities.
For the seven digits after the area code (part c), there are 8,000,000 possibilities.
Therefore, the total number of ten-digit phone numbers possible is 800 * 8,000,000 = 6,400,000,000.
For similar question on area codes.
https://brainly.com/question/29279031
#SPJ8
A point is plotted on a coordinate grid at (-3, 4). How far is the point from point (0, 0)?
Answers
The point at (-3, 4) is at a distance of 5 units from the point (0, 0).
How far is the point from (0, 0)?For two points (x₁, y₁) and (x₂, y₂), the distance between them is given by the formula:
distance = √( (x₁ - x₂)² + (y₁ - y₂)²)
In this case, we want to get the distance between (-3, 4) and (0, 0), using the above formula we will see that the distance is:
distance = √( (-3 - 0)² + (4 - 0)²) = √25 = 5
The distance is 5 units.
Learn more about distances between points:
https://brainly.com/question/7243416
#SPJ1
A. SSS Postulate
B. ASA Postulate
C. SAS Postulate
D. AAS Theorem

Answers
Answer:
B is the answer
Step-by-step explanation:
A phone receives signals from a transmitter that is 13km west and 21km south of it. what is the bearing from the phone to the transmitter? give your answer to the nearest degree

Answers
The bearing from the phone to the transmitter is approximately 31 degrees to the east of the north direction.
To determine the bearing from the phone to the transmitter, we can use trigonometry.
The bearing is typically measured clockwise from the north direction.
Given that the transmitter is 13 km west and 21 km south of the phone, we can form a right triangle with the phone as the vertex angle.
The side opposite to the vertex angle represents the north-south direction, and the side adjacent to the vertex angle represents the east-west direction.
Using the tangent function, we can calculate the angle:
tangent(angle) = (opposite side) / (adjacent side)
tangent(angle) = 21 km / 13 km
Taking the inverse tangent (arctan) of both sides, we find:
angle = arctan(21 km / 13 km)
Evaluating this using a calculator, we find the angle to be approximately 58.57 degrees.
However, since the bearing is measured clockwise from the north, we need to subtract this angle from 90 degrees (which represents the north direction) to obtain the bearing:
bearing = 90 degrees - 58.57 degrees
Calculating this, we find the bearing to be approximately 31.43 degrees.
For similar question on transmitter.
https://brainly.com/question/29221269
#SPJ8
Susan has 3 pairs of shorts, 5 shirts, and 2 pairs of shoes to take to camp. If she wears a pair of shorts, a shirt and pair of shoes each day, how many different outfit combinations does Susan have to choose from?
Answers
Answer:
30
Step-by-step explanation:
What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/IEnaK9Mnw3ftGn7VoWymvKjzqCukNTp6.png)
Answers
The given passage provides a proof that the Separation Axioms follow from the Replacement Schema.
The proof involves introducing a set F and showing that {a: e X : O(x)} is equal to F (X) for every X. Therefore, the conclusion is that the Separation Axioms can be derived from the Replacement Schema.In the given passage, the author presents a proof that demonstrates a relationship between the Separation Axioms and the Replacement Schema.
The proof involves the introduction of a set F and establishes that the set {a: e X : O(x)} is equivalent to F (X) for any given set X. This implies that the conditions of the Separation Axioms can be satisfied by applying the Replacement Schema. Essentially, the author is showing that the Replacement Schema can be used to derive or prove the Separation Axioms. By providing this proof, the passage establishes a connection between these two concepts in set theory.
Learn more about axioms here:
https://brainly.com/question/2857184
#SPJ8
Please help and hurry

Answers
The equation of the parabola with vertex at point (2, -11) and passes through the point (0, 5) is y = 4(x - 2)² - 11.
What is linear and quadratic equation?A straight line can be used to symbolise a function that is linear, meaning that for each unit change in the input, the output (y) changes by a fixed amount (x). While a parabola can be used to depict a function, a quadratic function has an output (y) that changes by a non-constant amount for each unit change in the input (x). In other words, a quadratic function curves because of the squared term in its equation.
Given, the parabola has vertex at point (2, -11) and passes through the point (0, 5).
Thus, the equation of parabola in vertex form is:
y = a(x - 2)² - 11
Now, the parabola passes through the point (0, 5) we have:
5 = a(0 - 2)² - 11
5 = 4a - 11
16 = 4a
a = 4
Hence, the equation of the parabola with vertex at point (2, -11) and passes through the point (0, 5) is y = 4(x - 2)² - 11.
Learn more about quadratic equation here:
https://brainly.com/question/30098550
#SPJ1
Please help me with this

Answers
Http/b263849
(02.02 MC)
If trapezoid ABCD was reflected over the y-axis, reflected over the x-axis, and rotated 180°, where would point A′′′ lie?
Trapezoid formed by ordered pairs A at negative 4, 1, B at negative 3, 2, C at negative 1, 2, D at 0, 1.
(1, −1)
(−4, 1)
(1, 1)
(−4, −1)
Answers
The location of point A''' after the three transformations would be (-4, 1).
To determine the location of point A''', we need to apply the three transformations (reflection over the y-axis, reflection over the x-axis, and rotation of 180°) to point A.
When a point is reflected over the y-axis, the x-coordinate is negated while the y-coordinate remains the same.
So, the reflection of point A (-4, 1) over the y-axis would be (4, 1).
When a point is reflected over the x-axis, the y-coordinate is negated while the x-coordinate remains the same. So, the reflection of point (4, 1) over the x-axis would be (4, -1).
When a point is rotated 180°, the x-coordinate and y-coordinate are both negated. So, the rotation of point (4, -1) by 180° would be (-4, 1).
To learn more on Transformation click:
https://brainly.com/question/11709244
#SPJ1
You are completing a math assessment. The number of questions you complete and the time it takes you to complete them have a proportional relationship, as shown in the table. Number of Questions 4 7 Time (in minutes) 6 ? How much time does it take to complete 7 questions? 3 minutes 5 minutes, 30 seconds 9 minutes 10 minutes, 30 seconds
Answers
It will take 10 minutes 30 seconds to complete seven questions.
What is direct proportionality?Direct proportion or direct variation is the relation between two quantities where the ratio of the two is equal to a constant value. Mathematically, direct proportionality is represented by a straight line and it equation is of the form -
y = kx
k = y/x
where [k] is the constant
Given is that the number of questions [y] completed and time [x] it takes to complete them are proportional to each other.
The number of questions [y] completed is proportional to time [x] it takes to complete them. This means that -
y \(\alpha\) x
y = kx
k = y/x
So, we can write -
y₁/x₁ = y₂/x₂
Substituting the values given in the table -
4/6 = 7/x₂
x₂ = (7 x 6)/4
x₂ = 21/2
x₂ = 10.5
x₂ = 10 minutes 30 seconds
Therefore, it will take 10 minutes 30 seconds to complete seven questions.
To solve more questions on direct proportionality, visit the link below-
brainly.com/question/20400984
#SPJ1
[The given question is not complete. Refer to image attached for clear and complete question]

Answer:
10 minutes 30 seconds is the correct answer
Step-by-step explanation:
I took the test and that is what i got
A map of the city of Memphis has a representative fraction of 1:24,000. If you measured a map distance of 5.0 inches between road intersections, how far apart are the intersections in actuality
Answers
The actual distance between the road intersections is 120000 inches.
ScalingScaling is the process in which the size of a figure or object is either increased or decreased by a factor k so as to create an image.
Let y represent the size in actuality and x represent the size in the map. Given that the scale used is 1:24000.
Hence for a map size of 5 inches:
y = 1/(1/24000) * 5 = 24000 * 5 = 120000 inches
The actual distance between the road intersections is 120000 inches.
Find out more on Scaling at: https://brainly.com/question/10253650
Andrew's fish tank measures
24 inches long, 10.5 inches
wide, and 13 inches high. What
is the volume of the fish tank?
MONS
Answers
15 volume of the fish tank
what are the x intercepts of y=4x^2-12x+4
Answers
The x-intercepts of the given equation 4x^2-12x+4 is -3/2
What is Quadratic equation ?
Quadratic equation can be defined as the equation in which it is in the form of ax^2+bx+c = 0
where c is a constant.
Given equation ,
y = 4x^2+12x+4
so we have to find the x-intercept , make y = 0
and we have to solve for the given quadratic equation
so,
we get
4x^2+12x+4 = 0
(2x)^2 + 9 + 12x = 0
(2x+3)^2 = 0
x = -3/2
There is double root unique intercept or tangent at x = -3/2
Therefore, The x-intercepts of the given equation 4x^2-12x+4 is -3/2
To learn more about Quadratic equation from the given link.
https://brainly.com/question/30098550
#SPJ1
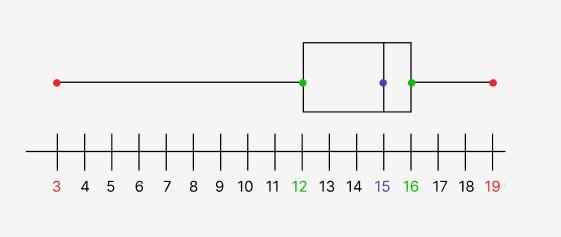
a hotel owner is deciding whether to buy new parts, hire a plumber, or allow no changes due to possible issues with the water pressure. to help make her decision, the data set lists the number of complaints about the water pressure at the hotel. for this data set, the minimum is 3, the median is 15, the third quartile is 16, the interquartile range is 4, and the maximum is 19. construct a box-and-whisker plot that shows the number of complaints. move the median first, then the first and third quartiles, and last the minimum and maximum.
Answers
A box-and-whisker plot shows the five-number summary of the data set, including the minimum value (3), first quartile (12), median (15), third quartile (16), and maximum value (19).
We know that the interquartile range is the third quartile minus the first quartile. The third quartile of the water pressure complaint data set is 16 and the interquartile range is 4, so the first quartile can be found by subtracting 4 from 16, which is 12.
The minimum value (3) is represented by the left end of the left whisker, the first quartile (12) is represented by the left edge of the box, the median (15) is represented by the line in the middle of the box, the third quartile (16) is represented by the right edge of the box, and the maximum value (19) is represented by the right end of the right whisker.
Read more about box-and-whisper plots:
brainly.com/question/12343132
#SPJ4
Add a term to the expression so tha it becomes a perfect square trinomial. Y^2-13y+

Answers
The term that should be added to the expression to make the expression perfect square trinomial is 169/4. The expression then becomes : (y - 13/2)²
What is meant by a perfect square trinomial?
By multiplying a binomial by another binomial, perfect square trinomials—algebraic equations with three terms—are created. A number can be multiplied by itself to produce a perfect square. Algebraic expressions known as binomials are made up of simply two words, each of which is separated by either a positive (+) or a negative (-) sign. Similar to polynomials, trinomials are three-term algebraic expressions.
A perfect square trinomial expression can be created by taking the binomial equation's square. If and only if a trinomial satisfying the criterion b² = 4ac has the form ax² + bx + c, it is said to be a perfect square.
Given expression y² - 13y + ?
Comparing with the general equation
a = 1
b = -13
For perfect square trinomial
b² = 4ac
(-13)² = 4 * 1 * c
169 = 4c
c = 169/4
So the expression becomes,
y² - 13y + 169/4 = (y - 13/2)²
Therefore the term that should be added to the expression to make the expression perfect square trinomial is 169/4.
To learn more about the perfect square trinomial, follow the link.
https://brainly.com/question/1538726
#SPJ1
Nathan works at an ice cream shop. The sugar cones have a diameter of 5.5 inches and a height of 3 inches. For a single-scoop cone, he packs the cone with ice cream and then puts a scoop on top. The scoop is approximately half a sphere. What is the volume of ice cream Nathan serves in a single scoop cone? Use 3.14 for pi. Round the volume to the nearest tenth.
Answers
The volume of ice cream Nathan serves in a single scoop cone is 67.32 in³.
What is the volume of the cone?The volume of a cone is calculated using the following formula as shown below;
V = ¹/₃πr²h
where;
r is the radius of the coneh is the height of the coneThe radius = d/2 = 5.5 in / 2 = 2.75 in
The volume of the cone is calculated as follows;
V = ¹/₃ x π x ( 2.75 in )² x 3
V = 23.76 in³
The /volume of the sphere is calculated as follows;
V = ⁴/₃ πr³
Since he added half of the volume of sphere, the new volume becomes;
V = ¹/₂ x ⁴/₃ πr³
V = ²/₃πr³
V = ²/₃π(2.75)³
V = 43.56 in³
The total volume = 23.76 in³ + 43.56 in³ = 67.32 in³
Learn more about volume of sphere here: https://brainly.com/question/10171109
#SPJ1
Anjie works on the weekends. Last Saturday she worked 7.75 hours and on Sunday she worked 8.5 hours. She earns $11 per hour. How much did she earn last weekend?
Answers
Hence, last weekend, Anjie earned $178.75.
Hoped this helped.
\(BrainiacUser1357\)
what is the y intercept ??

Answers
There is a ratio of 5 apples to 3 pears in a basket. There are 24 pears in the basket. How many apples are in the basker?
Answers
Answer:
There are 40 apples in the basket.
This is because 5 apples to 3 pears have a difference of 1.66666667 when dividing 5 by 3 to show the ratio difference. Then, all you do is multiply this number by the number of total pears which would look like 24 x 1.66666667 = 40.
I hope this helped you, have an amazing day! :)
5 pts
Question 6
Write the first five terms of the geometric sequence where Q1
Sand r = 3
O {8, 24, 72, 216, 648}
O {8, , , ,
O {3, 24, 192, 1536, 9216}
O {8, 11, 14, 17, 20}
5 pt
Question 7
Answers
Answer:
{8, 24, 72, 216, 648}
Step-by-step explanation:
Geometric sequence:
In a geometric sequence, the quotient of consecutive terms is always the same, that is, each term is the previous term multiplied by the common ratio.
In this question:
First element is 8, common ratio of 3. So
Second term: 8*3 = 24
Third term: 24*3 = 72
Fourth term: 72*3 = 216
Fifth term: 216*3 = 648
So the answer is {8, 24, 72, 216, 648}
Solve the initial-value problem: y" - 4y' + 8y = 0, y(0) = 1, y'(0) = 2.
Answers
Answer:
The solution of the problem is \(y(t) = e^{2 t} cos(2 t)\)
Step-by-step explanation:
First we will write the characteristic equation which is
\(x^{2} -4x + 8 = 0\)
Now, we will solve this quadratic equation using the general formula.
Given a quadratic equation of the form, \(ax^{2} +bx +c = 0\), then
From the general formula,
\(x = \frac{-b+\sqrt{b^{2}-4ac } }{2a}\) or \(x = \frac{-b-\sqrt{b^{2}-4ac } }{2a}\)
From the characteristic equation, \(a = 1, b = -4,\) and \(c = 8\)
Hence,
\(x = \frac{-(-4)+\sqrt{(-4)^{2}-4(1)(8) } }{2(1)}\) or \(x = \frac{-(-4)-\sqrt{(-4)^{2}-4(1)(8) } }{2(1)}\)
\(x = \frac{4+\sqrt{-16} }{2}\) or \(x = \frac{4-\sqrt{-16} }{2}\)
\(x = \frac{2+4i }{2}\) or \(x = \frac{2-4i }{2}\)
\(x = 2 + 2i\) or \(x = 2 - 2i\)
That is, \(x\) = \(2\) ± \(2i\)
Then, \(x_{1} = 2 + 2i\) and \(x_{2} = 2 - 2i\)
These are the roots of the characteristic equation
The roots of the characteristic equation are complex, that is, in the form
(\(\alpha\) ± \(\beta i\)).
For the general solution,
If the roots of a characteristic equation are in the form (\(\alpha\) ± \(\beta i\)), the general solution is given by
\(y(t) = C_{1}e^{\alpha t} cos(\beta t) + C_{2}e^{\alpha t} sin(\beta t)\)
From the characteristic equation,
\(\alpha = 2\) and \(\beta = 2\)
Then, the general solution becomes
\(y(t) = C_{1}e^{2 t} cos(2 t) + C_{2}e^{2 t} sin(2t)\)
Now, we will determine \(y'(t)\)
\(y'(t) = 2C_{1}e^{2 t} cos(2 t) - 2C_{1}e^{2t}sin(2t) + 2C_{2} e^{2t}sin(2t) +2C_{2}e^{2t}cos(2t)\)
From the question,
y(0) = 1
and
y'(0) = 2
Then,
\(1 = y(0) = C_{1}e^{2 (0)} cos(2 (0)) + C_{2}e^{2 (0)} sin(2(0))\)
\(1 = C_{1}e^{ 0} cos(0) + C_{2}e^{0} sin(0)\)
(NOTE: \(e^{0} = 1, cos(0) = 1\) and \(sin(0) = 0\) )
Then,
\(1 = C_{1}\)
∴\(C_{1} = 1\)
Also,
\(2 = y'(0) = 2C_{1}e^{2 (0)} cos(2 (0)) - 2C_{1}e^{2(0)}sin(2(0)) + 2C_{2} e^{2(0)}sin(2(0)) +2C_{2}e^{2(0)}cos(2(0))\)\(2 = 2C_{1}e^{0} cos(0) - 2C_{1}e^{0}sin(0) + 2C_{2} e^{0}sin(0) +2C_{2}e^{0}cos(0)\)
\(2 = 2C_{1} +2C_{2}\)
Then,
\(1 = C_{1} +C_{2}\)
\(C_{2} = 1 - C_{1}\)
Recall, \(C_{1} = 1\)
∴ \(C_{2} = 1 - 1 = 0\)
\(C_{2} = 0\)
Hence, the solution becomes
\(y(t) = e^{2 t} cos(2 t)\)
