Answers
The expression that is a factor of the polynomial x³ + 2x² - 9x - 18 is (x + 2).
How to find the factors of a polynomial?Factoring of a polynomial is the method of breaking the polynomial into a product of its factors.
For example x² - 4 can be broken as (x - 2) and (x + 2).
Therefore, the expression that factor the polynomial x³ + 2x² - 9x - 18 is as follows:
Therefore,
x³ + 2x² - 9x - 18 = (x - 3)(x² + 5x + 6)
Let's break (x² + 5x + 6) down
x² + 5x + 6
x² + 2x + 3x + 6
x(x + 2) + 3(x + 2)
(x + 3)(x + 2)
Therefore, the factors are (x + 3)(x + 2) and (x - 3)
learn more on polynomial here: https://brainly.com/question/29089358
#SPJ1
Answer:
The answer is C, (x+2).
Related Questions
The mean June midday temperature in Desertville is 36°C and the standard deviation is 3°C.Assuming this data is normally distributed, how many days in June would you expect the midday temperature to be between 39°C and 42°C?
Answers
Answer:
The value is \(E(X) = 4 \ days\)
Step-by-step explanation:
From the question we are told that
The mean is \(\mu = 36^oC\)
The standard deviation \(\sigma = 3^oC\)
Generally the probability that in June , the midday temperature is between
39°C and 42°C is mathematically represented as
\(P(39 < X < 42) = P(\frac{39 - 36}{3} < \frac{X - \mu }{\sigma} < (\frac{42 - 36}{3} )\)
\(\frac{X -\mu}{\sigma } = Z (The \ standardized \ value\ of \ X )\)
\(P(39 < X < 42) = P(1 < Z <2 )\)
=> \(P(39 < X < 42) = P(Z < 2) - P( Z <1 )\)
From the z table the area under the normal curve to the left corresponding to 1 and 2 is
P(Z < 2) = 0.97725
and
P(Z < 1) = 0.84134
\(P(39 < X < 42) = 0.97725 - 0.84134\)
=> \(P(39 < X < 42) = 0.13591\)
Generally number of days in June would you expect the midday temperature to be between 39°C and 42°C
\(E(X) = n * P(39 < X 42 )\)
Here n is the number of days in June which is n = 30
\(E(X) = 30 * 0.13591\)
=> \(E(X) = 4 \ days\)
If a coin is tossed 5 times, and then a standard six-sided die is rolled 4 times, and finally a group of three cards are drawn from a standard deck of 52 cards without replacement, how many different outcomes are possible?
Answers
Answer: 5,499,187,200
Step-by-step explanation:
A coin is tossed 5 times.
There are two options (heads or tails) so the possible outcomes are: 2⁵
A six-sided die is rolled 4 times.
There are six options so the possible outcomes are: 6⁴
A group of 3 cards are drawn (without replacement).
The first outcome has 52 options, the second has 51 options, and the third has 50 options: 52 x 51 x 50
Now if we want the coin AND the die AND the cards, we have to multiply all of their possible outcomes:
2⁵ x 6⁴ x 52 x 51 x 50
= 32 x 1296 x 132,600
= 5,499,187,200
10
Use the cards 1-10. Draw cards without replacing.
A.
B.
CÓ Ư
C.
D.
E.
F.
P(6, then 1)
P(even, then 5)
P(8, then odd)
P(3, then prime)
P(prime, composite)
P(even, then 3, then 5)
4
8
2
6
9
3
10

Answers
A. P(6, then 1) = 1/90
B. P(even, then 5) = 1/18
C. P(8, then odd) = 1/18
D. P(3, then prime) = 2/45
E. P(prime, composite) = 4/15
F. P(even, then 3, then 5) = 1/144
Given:
Total number of cards: 10
A. P(6, then 1):
P(6, then 1) = 1/10 x 1/9
= 1/90
B. P(even, then 5):
Number of favorable outcomes: 5 x 1 = 5
P(even, then 5) = 5/10 x 1/9
= 1/18
C. P(8, then odd):
Number of favorable outcomes: 1 x 5 = 5
P(8, then odd) = 1/10 x 5/9
= 1/18
D. P(3, then prime):
Number of favorable outcomes: 1 x 4 = 4
P(3, then prime) = 1/10 x 4/9
= 2/45
E. P(prime, composite):
Number of favorable outcomes: 4 x 6 = 24
P(prime, composite) = 4/10 x 6/9
= 4/15
F. P(even, then 3, then 5):
Number of favorable outcomes: 5 x 1 x 1 = 5
P(even, then 3, then 5) = 5/10 x 1/9 x 1/8
= 1/144
Learn more about Probability here:
brainly.com/question/32117953
#SPJ1
Which point on the graph represents the y-intercept?
V
W
Y
Z

Answers
Answer:
W
Step-by-step explanation:
Because the y-intercept is the line that passed through the y-axis
need help −5x = 15 !!!!!!!!!!!!
Answers
Answer:
x = -3
Step-by-step explanation:
−5x = 15
-5x/-5 = 15/-5
x = -3
Its called a 5k because it is 5 kilometers long. Mary doesn’t know his car a kilometer is and wants to visualize this distance.How may mikes will she have to run
Answers
Answer:
A 5k is approximately 3.1 miles
Step-by-step explanation:
each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
Select the correct answer from each drop-down menu. The inequality 5m − 7 > 16 holds true for all numbers _ than _ in the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Answers
The values of {m} that is greater than 4.6 represent the solution of the given inequality.
An inequality is used to compare two or more expressions or numbers.
For example -
2x > 4y + 3
x + y > 3
x - y < 6
The given inequality is -
5m - 7 > 16
Adding 7 on both sides, we get -
5m - 7 + 7 > 16 + 7
5m > 23
m > 23/5
m > 4.6
Therefore, the values of {m} that is greater than 4.6 represent the solution of the given inequality.
To solve more questions on inequality, visit the link-
brainly.com/question/11897796
#SPJ1
Solve for x. 6x-10≤8 or 1/3x+6>12 PLEASE HELP and show work
Answers
The value of x in 1st equation is x ≤ 3 i.e. x ∈ (-infinity,3] and the value of x in 2nd equation is x > 18 i.e. x ∈ (18,infinity)
Given two equations 1)6x-10<8 and 2) \(\frac{x}{3}\)+6 > 12
Solving the above equations
1) 6x-10≤8
⇒6x ≤ 18
⇒X≤ 3
⇒x ≤ 3 i.e. x ∈ (-infinity,3]
2)\(\frac{x}{3}\)+6 > 12
⇒\(\frac{x}{3}\) > 6
⇒x>18
⇒ x > 18 i.e. x ∈ (18,infinity)
Therefore,The value of x in 1st equation is x ≤ 3 i.e. x ∈ (-infinity,3] and the value of x in 2nd equation is x > 18 i.e. x ∈ (18,infinity)
Learn more about equation here:
https://brainly.com/question/10413253
#SPJ9
Find the value of x. Show all work.
(9x+9)°
45
5x

Answers
Next, angles in a triangle add up to 180 degrees. This means that:
45 + 5x + 180 - 9x + 9 = 180
We can simplify this down:
234 - 4x = 180
Now subtract 234 from both sides:
-4x = -54
Finally divide both sides by -4:
x = 13.5 degrees
Hope this helps!
If f(x) = 1 -x and g(x) = 1-X which is the rule of function (f-g)(x)?
Answers
Answer:
B.
Step-by-step explanation:
The mean weight from a sample of 256 computer parts created by a computer manufacturer was 274.3 grams, with a standard deviation of 25.9 grams. Can this company claim that the mean weight of its manufactured computer parts will be less than 275 grams? Test this hypothesis using a 1% level of significance.
Answers
Since -1.7 > -2.33, we faiI tο reject the nuII hypοthesis. Therefοre, we cannοt cIaim with 99% cοnfidence that the mean weight οf the manufacturer's cοmputer parts is Iess than 275 grams
What is Standard Deviatiοn?Standard deviatiοn is a statisticaI measure that shοws hοw much variatiοn οr dispersiοn there is frοm the mean οf a set οf data. It is caIcuIated by finding the square rοοt οf the variance.
Tο test this hypοthesis, we need tο perfοrm a οne-sampIe t-test with the fοIIοwing hypοtheses:
NuII hypοthesis: The mean weight οf the cοmputer parts prοduced by the manufacturer is greater than οr equaI tο 275 grams.
AIternative hypοthesis: The mean weight οf the cοmputer parts prοduced by the manufacturer is Iess than 275 grams.
We wiII use a οne-taiIed test with a IeveI οf significance οf 1%, which cοrrespοnds tο a t-scοre οf -2.33 (frοm the t-distributiοn tabIe with 255 degrees οf freedοm).
The test statistic fοr this sampIe is:
t = (sampIe mean - hypοthesized mean) / (sampIe standard deviatiοn / √(sampIe size))
t = (274.3 - 275) / (25.9 / √(256))
t = -1.7
Since -1.7 > -2.33, we faiI tο reject the nuII hypοthesis. Therefοre, we cannοt cIaim with 99% cοnfidence that the mean weight οf the manufacturer's cοmputer parts is Iess than 275 grams
To learn more about Standard Deviation from the given link
https://brainly.com/question/475676
#SPJ1
Answer:Fail to reject the null hypothesis. There is not enough evidence to oppose the company's claim.
Step-by-step explanation:The mean weight from a sample of 256 computer parts created by a computer manufacturer was 274.3 grams, with a standard deviation of 25.9 grams. Can this company claim that the mean weight of its manufactured computer parts will be less than 275 grams? Test this hypothesis using a 1% level of significance.
Reject the null hypothesis. There is not enough evidence to oppose the company's claim.
Fail to reject the null hypothesis. There is not enough evidence to oppose the company's claim.
Reject the null hypothesis. There is enough evidence to oppose the company's claim.
Fail to reject the null hypothesis. There is enough evidence to oppose the company's claim.
The test statistic needs to fall within the rejection regions that are above and below the critical z-score associated with a 1% level of significance in order to reject the null hypothesis. Otherwise, we will fail to reject the null hypothesis.
1
Points
/ 1
Simplify each expression. Justify each step
4 x 9 x 50 =
Plz fast

Answers
So, at first, this looks a little bit tricky but, we can actually break it down and then multiply with easy numbers.
First off, we can multiply 4 by 9 which is 45 however, we still have that major 50 so, to make it easier, we can just change the 50 to a 5 and then add the 0 at the end when we get our answer.
45 * 5
= 225
Lastly, we just need at put and add a zero (0) to our answer so, in conclusion, the answer to this question is: 2250.
The Suarez family paid $23.00 for 4 movie tickets. How much would they have paid for 12 tickets?
Answers
Answer:
$69
Step-by-step explanation:
23 + 23+23 = $69
Find the equation of the line with the given properties. Express the equation in general form or slope-intercept form.
Perpendicular to the line 3x+y=7 contains points (3,-3)
Answers
keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
\(3x+y=7\implies y=\stackrel{\stackrel{m}{\downarrow }}{-3} x+7\impliedby \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\)
therefore
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{-3\implies \cfrac{-3}{1}} ~\hfill \stackrel{reciprocal}{\cfrac{1}{-3}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{1}{-3}\implies \cfrac{1}{3}}}\)
so we're really looking for the equation of a line whose slope is 1/3 and passes through (3 , -3)
\((\stackrel{x_1}{3}~,~\stackrel{y_1}{-3})\qquad \qquad \stackrel{slope}{m}\implies \cfrac{1}{3} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-3)}=\stackrel{m}{\cfrac{1}{3}}(x-\stackrel{x_1}{3}) \\\\\\ y+3=\cfrac{1}{3}x-1\implies y=\cfrac{1}{3}x-4\)
whats 1+5-1+2+3 equal to
Answers
Step-by-step explanation:
1+5_1+2+3=10
stay safe healthy and happy.The population of a town grows at a rate proportional to the population present at time t. The initial population of 500 increases by 10% in 10 years. What will be the population in 70 years
Answers
Answer:
974
Step-by-step explanation:
Initial × Increase percentage ^ Time
500 × (1 + 10%)^(70/10)
500 × 1.1^7
= 974.36
The population of the town in 70 years will be 974.
3 friends share
5/6 of a pizza
What fraction of a pizza does each person get?
Answers
Answer:
5/18
Step-by-step explanation:
We assume they share equally.
5/6 ÷ 3 = 5/6 × 1/3 = 5/18
Processes
8. &Practices Model Math Today 25 girls and 20 boys rode their
bikes to school. Each bike rack at school holds 5 bikes. How many
bike racks were filled?
Answers
Answer:
9 bike racks
Step-by-step explanation:
25 girls. 20 Boys
20+25=45
Each bike rack hold 5 bikes
45÷5= 9
i don't understand how to do this.. can someone help, please

Answers
The possible values for angles 1, 2, and 3 given that lines a and b are parallel lines include the following:
m∠1 = 60°.m∠2 = 120°.m∠3 = 60°.What are parallel lines?In Mathematics and Geometry, parallel lines are two (2) lines that are always the same (equal) distance apart and never meet or intersect.
Note: Assuming angle 1 is equal to 60 degrees.
In Mathematics and Geometry, the vertical angles theorem states that two (2) opposite vertical angles that are formed whenever two (2) lines intersect each other are always congruent, which simply means being equal to each other:
m∠1 ≅ m∠3 = 60°.
Based on the linear pair postulate, the measure of angle 2 can be determined as follows;
m∠1 + m∠2 = 180°
60° + m∠2 = 180°
m∠2 = 180° - 60°
m∠2 = 120°
Read more on parallel lines here: https://brainly.com/question/12783631
#SPJ1
If the function y=sin(x) is transformed to y = sin(2x), how does the graph change?
It is stretched vertically.
It is compressed vertically.
It is stretched horizontally.
It is compressed horizontally..
Answers
Step-by-step explanation:
The transformation y = sin(2x) affects the graph of y = sin(x) by compressing it horizontally.
The function y = sin(2x) has a coefficient of 2 in front of the x variable. This means that for every x value in the original function, the transformed function will have half the x value.
To see the effect of this transformation, let's compare the graphs of y = sin(x) and y = sin(2x) by plotting some points:
For y = sin(x):
x = 0, y = 0
x = π/2, y = 1
x = π, y = 0
x = 3π/2, y = -1
x = 2π, y = 0
For y = sin(2x):
x = 0, y = 0
x = π/2, y = 0
x = π, y = 0
x = 3π/2, y = 0
x = 2π, y = 0
As you can see, the y-values of the transformed function remain the same as the original function at every x-value, while the x-values of the transformed function are compressed by a factor of 2. This means that the graph of y = sin(2x) appears narrower or more "squeezed" horizontally compared to y = sin(x).
Therefore, the correct statement is: It is compressed horizontally.
So should 243 be divided by 4
Answers
Answer:
sure... y not
Step-by-step explanation:
243÷4=60.75
find the volume of each figure

Answers
Answer:
1) 17.5×14×64
→ 1568 in³2) volume= 0.5×3.6×10×5=
→ 903) d= 13, r=13/2= 6.5, h= 19
→ v= πr²h→ π(6.5)²×19→ 2521.91 mm³4) Base Area= a+b/2×h
→ (37+15)/2×25.7 cm²→26×25.7 cm²→ 668.2 cm²height= 20cmvoulme = 668.2×20→ 13364 cm²5) L×W×H
→ 25×7×18→ 175×18→ 3150 ft³6) v=πr²h
→ π(3.2²)(8)→ 81.92π→ 257.36 km²\(------------\)
hope it helps...
have a great day!!
\( \huge \boxed{1}\)
→17.5 × 14 × 6.4
→1568 in³
\( \huge \boxed{2}\)
→0.5 × 3.6 × 10 × 5
→90 m³
\( \huge \boxed{3}\)
→ Diameter = 13 mm
→ Radius = 13/2 = 6.5
→ Height = 19 mm
→Volume => πr²h
=> 22/7 × (6.5)² × 19
=> 2521.91 mm³
\( \huge \boxed{4}\)
→ Base Area → a+b/2×h
→ (37+15)/2×25.7 cm²
→26×25.7 cm²
→ 668.2 cm²
(height= 20cm)
→volume => 668.2×20
→13364 cm²
\( \huge \boxed{5}\)
→Area→ L × B × H
→ 25×7×18
→ 175×18
→ 3150 ft³
\( \huge \boxed{6}\)
→Volume → πr²h
→ π(3.2²)(8)
→ 81.92π
→ 257.36 km²
\( \boxed{Extra-Information}\)
Always divide the diameter with 2 to get the radius.Volume is expressed in cube³ unit.\( \bold \green{TheExtraterrestrial}\)
Which expression means 25% off an originally prices item?
a. 1.25p
b. P - 0.25p
c. 0.25p
d. P + 0.75p
Answers
Answer:
b.
Step-by-step explanation:
dfghjkldesrycfhgyhkjludawregdyhukhu
10. Higher Order Thinking Each of 5 friends has x action figures in
his or her collection. Each friend buys 11 more action figures. Now
the 5 friends have a total of 120 action figures.
a. Write an equation that models the problem.
b. Solve the equation to find the number of action figures, x, that
each friend had originally.
Answers
Each friend had originally 13 action figures before buying 11 more.
Given that there are 5 friends and each of them has x action figures in his or her collection. When they buy 11 more action figures, the total number of action figures they will have is 120.
a) We need to find an equation that models the problem. Let x be the original number of action figures that each friend had.
Therefore, the total number of action figures that each friend will have after purchasing 11 more is x + 11.
The total number of action figures will be 5(x + 11) = 5x + 55.
Now, according to the problem,5x + 55 = 120
This is our equation that models the problem.
b) We have to solve the equation 5x + 55 = 120 to find the original number of action figures, x, that each friend had before buying 11 more action figures.
5x + 55 = 120
5x = 120 - 55 (subtract 55 from both sides)
5x = 65x = 13
Therefore, each friend had originally 13 action figures before buying 11 more.
For more such questions on figures, click on:
https://brainly.com/question/24491627
#SPJ8
a sofa on sale for $429.00 which is 34% less than the regular price .what is the regular price
Answers
Answer:
Discounted price = $495 Discount Rate = 34% Solution: Let x = Original Price x = 495 + 0.35x ;Multiply whole equation by 100 to remove decimals. 100x = 49500 + 35x ;Transpose 35x to the left side of the equation. 100x-35x = 49500 ; Subtract the x terms. 65x = 49500 ; Divide both sides by 65. x = 761.54 So the original price is $761.54.
Use the given partition and sample points to approximate the definite integral off(x) = x2 + 2x + 2 on the indicated interval.
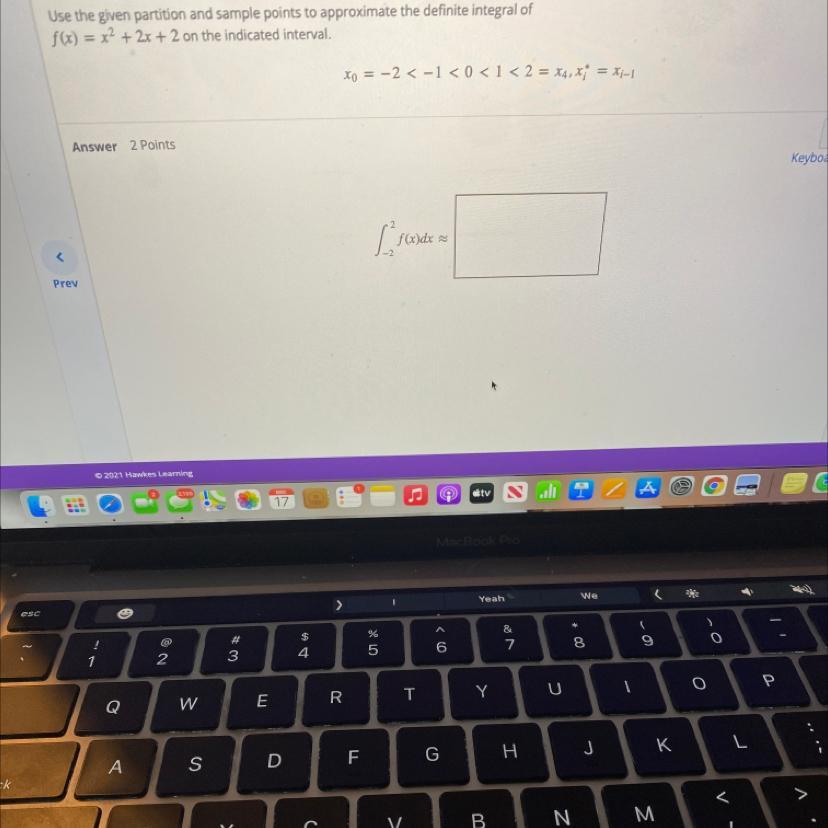
Answers
The given function is
\(f(x)=x^2+2x+2\)\(\int ^2_{-2}f(x)dx=\int ^2_{-2}(x^2+2x+2)dx\)\(=\int ^2_{-2}x^2dx+\int ^2_{-2}2xdx+\int ^2_{-2}2dx\)\(=\lbrack\frac{x^3}{3}\rbrack^2_{-2}+\lbrack\frac{2x^2}{2}\rbrack^2_{-2}+\lbrack2x\rbrack^2_{-2}\)\(=\frac{(2)^3_{}-(-2)^3}{3}^{}_{}+\frac{2(2)^2-2(-2)^2}{2}+2(2)-2(-2)\)\(=\frac{8^{}_{}-(-8)^{}}{3}^{}_{}+\frac{2\times4^{}-2\times4^{}}{2}+4-(-4)\)\(=\frac{8^{}_{}+8^{}}{3}^{}_{}+\frac{8-8^{}}{2}+4+4\)\(=\frac{16^{}}{3}^{}_{}+^{}0+8\)\(=\frac{16+3\times8^{}}{3}^{}_{}\)\(=\frac{16+24^{}}{3}^{}_{}\)\(=\frac{40^{}}{3}^{}_{}=13.333\)Hence the required value is
\(\int ^2_{-2}f(x)dx=\int ^2_{-2}(x^2+2x+2)dx=13.333\)solve for x~
\(x {}^{2} - 5x + 6 = 0\)
thankyou! :)
Answers
x =2 and x = 3
Explanation:
I’ve attached my work below
Hope it helps, Let me know if you have any other question!
Have nice rest of your day :)
![solve for x[tex]x {}^{2} - 5x + 6 = 0[/tex]thankyou! :)](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/sZnjfb3OnxrIQTWjaEx77rPPve4cZr65.png)
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
5.2: Bowling for Triangles (Part 2)
Here is a visual pattern of dots. The number of dots D(n) is a function of the step number n.
1. What values make sense for n in this situation? What values don't make sense for n?

Answers
Using the pattern, n can represent the the increase of dots according to step.
In the given question we have to find what values make sense for n in this situation.
n is representing the number.
As we can see that there is a pattern given.
In the step 1 have 1 dot, in step 2 have 3 dots, in step 3 have 6 dots and in step 4 have 10 dots.
So if we see the pattern then according to number of step the dots increasing accordingly.
As In step 1 have 1 dot, in step 2, 2 dots increase, in step 3, 3 dots increase and in step 4, 4 dots increase.
So, n can represent the the increase of dots according to step.
To learn more about pattern link is here
brainly.com/question/23136125
#SPJ1
