plot the points in the x-y table. Drag the points to the correct location on the coordinate plane

Answers
Answer:
(See the graph)
Step-by-step explanation:
Red:
(-2, 10)
Left two, up ten
Blue:
(-1, 6)
Left one, up six
Green:
(0, 2)
Up two
Purple:
(1, -2)
Right one, down two

Related Questions
In the cryptarithm shown with sum 700, different letters stand for different digits, and no letter represents the digit 7 or 0. How many different numeric values for "SAT" are possible?
SAT+SUN=700
Answers
Answer:
The number of possible numeric value for SAT are 8 possible numeric values
Step-by-step explanation:
A cryptarithm is a form of mathematical game where unknown numbers represented by letters of the alphabet are used to form mathematical equations
The given cryptarithm is SAT + SUN = 700
The parameters are;
The digits represented by the letters are different
Non of the digits represented by the letters equals 7 or 0
We have;
T + N = 10
1 + A + U = 10
1 + S + S = 7
Therefore, S = (7 - 1)/2 = 3
S = 3
A + U = 10 - 1 = 9
A + U = 9
Therefore, A = 4 or 5 (2 choices)
From T + N = 10
T = 1, 2, 8, or 9 (4 choices) similarly, N = 1, 2, 8, or 9 (4 choices)
Therefore, the number of numeric values that SAT represent is given as follows;
(S = 1 choice) × (A = 2 choices) × (T = 4 choices) = 1 × 2 × 4 = 8 numeric values
SAT has 8 possible numeric value
When spinning a wheel with 1 red, 2 blue, and 3 green spaces, what
is the probability that you will not spin a red?
Answers
Step-by-step explanation:
so, we have 1 + 2 + 3 = 6 total spaces.
a probability is always the ratio
desired cases / totally possible cases
the probability to spin red is therefore
1 desired case
6 total possible cases
1/6 = 0.166666666...
a probability of 1 means a sure result = anyone of the totally possible cases.
so, 6/6 = 1 in our case.
if the desired cases are everything but red, we need to eliminate the possible red results (1) from the amount of our desired cases : 6 - 1 = 5
so the probability of not spinning a red is
5/6 = 0.833333333...
formally we can also say this is the sure thing minus the opposite of what we want to have. the opposite of not spinning a red is spinning a red (1/6) :
1 - 1/6 = 5/6 = 0.833333333...
a study will be conducted to construct a 90% confidence interval for a population proportion. an error of 0.2 is desired. there is no knowledge as to what the population proportion will be. what sample size is required ?
Answers
A sample size of 17 is required to construct a 90% confidence interval for a population proportion with an error of 0.2.
To determine the sample size required to construct a 90% confidence interval for a population proportion with an error of 0.2 (or 20%), we need to use the formula for sample size calculation in proportion estimation.
The formula for sample size in proportion estimation is:
n = (Z² * p * q) / E²
Where:
n = required sample size
Z = Z-score corresponding to the desired confidence level (90% confidence level corresponds to a Z-score of approximately 1.645)
p = estimated or assumed population proportion (since there is no knowledge about the population proportion, we can assume a conservative value of 0.5 to get the maximum sample size)
q = 1 - p (complement of p)
E = desired margin of error (0.2 or 20% in this case)
Substituting the values into the formula:
n = (1.645² * 0.5 * (1 - 0.5)) / 0.2²
n = (2.705 * 0.5 * 0.5) / 0.04
n = 0.67625 / 0.04
n ≈ 16.90625
Since the sample size must be a whole number, we round up the result to the nearest whole number:
n = 17
Therefore, a sample size of 17 is required to construct a 90% confidence interval for a population proportion with an error of 0.2.
It's important to note that this calculation assumes maximum variability in the population proportion (p = 0.5) to ensure a conservative estimate. If there is any information or prior knowledge available about the population proportion, it should be used to refine the sample size calculation.
for more such question on interval visit
https://brainly.com/question/30460486
#SPJ8
2 V The soccer field at Niall's school is 98 meters long and 55 meters wide. What is the perimeter of the field?
Answers
Perimeter of the soccer field is 306 meters.
What is perimeter?A shape's perimeter is defined as the total length of its bounds. The perimeter of a shape is determined by summing all sides and side lengths that enclose the shape. It is measured in linear measurement units such as centimeters, meters, inches, and feet.
Given,
Length of the soccer field = 98 meters
Width of the soccer field = 55 meters wide
Perimeter of rectangle = 2(Length + Width)
Perimeter of soccer field = 2(98 + 55)
Perimeter of soccer field = 2(153)
Perimeter of soccer field = 306 meters
Hence, 306 meters is the perimeter of the soccer field.
Learn more about perimeter here:
https://brainly.com/question/6465134
#SPJ1
Q
100%
Solve for x.
3x + 14 = 20
o
A. 2
B. 45
o
C. 8
OD. 25.
Answers
Answer:
A
Step-by-step explanation:
3x+14=20
Here you need to do the inverse operation of +14 to isolate the 3x. The inverse operation would be -14 so you subtract 14 on both sides.
3x+14=20
-14 -14
3x=6
Now you have 3x=6 so you have to do the inverse operation of times 3. The inverse of that is dividing so you divide 3 by 3 and 6 by 3. 3/3 is 1 and 6/3 is 2
(3/3)x=(6/3)
x=2
Suppose that A is a subset of\mathbb{N}and(1) 0,1 ∈ A(2) if n ∈ A, then 4n ∈ A.Give a careful proof that {4n : n ∈\mathbb{N}} is a subset of A. (Apply induction on n.)
Answers
If A is a subset of\mathbb{N}and(1) 0,1 ∈ A(2) if n ∈ A, then 4n ∈ A.
To prove that {4n : n ∈ N} is a subset of A using induction, we need to follow these steps:
1. Base Case: Prove the statement is true for the smallest value of n, which is n=0 in this case.
2. Inductive Hypothesis: Assume the statement is true for n=k, where k is an arbitrary natural number.
3. Inductive Step: Prove the statement is true for n=k+1 using the inductive hypothesis.
Step 1: Base Case (n=0)
For n=0, we have 4*0=0. Since 0 ∈ A according to condition (1), the statement is true for n=0.
Step 2: Inductive Hypothesis
Assume that for some k ∈ N, 4k ∈ A. This is our inductive hypothesis.
Step 3: Inductive Step (n=k+1)
We need to prove that 4(k+1) ∈ A. Since 4k ∈ A from the inductive hypothesis, and we know from condition (2) that if n ∈ A, then 4n ∈ A, we can apply this condition to 4k:
4(4k) ∈ A
Now, we can simplify this expression:
4(k+1) = 4k + 4 = 4(4k)
Therefore, 4(k+1) ∈ A.
Since we've proven the statement for the base case and the inductive step, we can conclude by induction that {4n : n ∈ N} is a subset of A.
To know more about Inductive Hypothesis refer here:
https://brainly.com/question/30434803
#SPJ11
suzy randomly picks marbles from a bag containing 12 identical marbles. how many possible outcomes are there if she selects 9 marbles?
Answers
There are 12 identical marbles in a bag, and Suzy is going to select 9 marbles from the bag at random.
The problem asks how many possible outcomes there are.
To begin with, we need to understand the concept of combinations. A combination is a way to select a subset of objects from a larger set, without regard to the order of the objects. For example, if we have four marbles (A, B, C, and D), there are six possible combinations of two marbles: AB, AC, AD, BC, BD, and CD.
In this problem, we have 12 marbles and we are choosing 9 of them. To find the total number of combinations, we can use the formula for combinations:
nCr = n! / r!(n-r)!
where n is the total number of objects, r is the number of objects we are choosing, and ! represents factorial (i.e. multiplying a number by all the positive integers less than it).
So, plugging in our numbers:
12C9 = 12! / 9!(12-9)! = 12! / 9!3! = (121110) / (321) = 220
Therefore, there are 220 possible outcomes if Suzy selects 9 marbles at random from a bag containing 12 identical marbles.
To learn more about combinations click brainly.com/question/13715183
#SPJ11
The diagonal of a polygon is directly proportional to its
perimeter. The perimeter of the polygon having a diagonal
of 8 units, is equal to 36 units. What is the perimeter of a
polygon having a diagonal of 10 units
Answers
Answer:
45 units
Step-by-step explanation:
Given that the perimeter and diagonal length of a polygon are proportional and that a polygon with a diagonal of 8 units has a perimeter of 36 units, you want the perimeter for a diagonal of 10 units.
ProportionThe proportion of interest is ...
P/d = p/10 = 36/8
Multiplying by 10 gives ...
p = 10(36/8) = 45
The perimeter of the larger polygon is 45 units.
Donald plays with his wood cubes and decides to make pyramids.
He carries on with his pyramids and labels following the same pattern.
After making p4 donald realises that he only has 12 wood cubes left. How many more cubes will he need to make p5?
Answers
Donald would need to use 5 levels of cubes, So to make p5 he would need 25-12 = 13 more cubes.
What is pyramid?A pyramid is a structure with a square or triangular base and four triangular sides that meet at a point, called the apex. Pyramids were built by ancient civilizations, such as the Egyptians, as tombs for pharaohs and their queens.
What is pyramid levels?In the context of building pyramids with wood cubes, it seems like "pyramid levels" refers to the layers of cubes used to construct the pyramid. Each level is a layer of cubes that sits on top of the previous one, and the number of cubes in each level increases as you move up the pyramid. For example, in the case of p4, the base level would use 1 cube, the next level would use 4 cubes, the next level would use 9 cubes, and so on. The top level, which forms the apex of the pyramid, would use the most cubes. So the pyramid levels refer to the different layers of the pyramid and the number of cubes used in each layer.
To make a pyramid labeled p5, Donald would need to use 5 levels of cubes.
Donald uses 1 cube for the base of p4, 4 cubes for the next layer, 9 cubes for the next, 16 cubes for the next and 25 cubes for the top level.
So to make p5 he would need 25-12 = 13 more cubes.
To know more about pyramid visit:
https://brainly.com/question/14091039
#SPJ4
Find the median for the data given. Number of steaks served: 8, 9, 19, 28, 33, 37, 46
Answers
Answer:
Therefore, the median for the given data set is 28.
Step-by-step explanation:
To find the median for the given data set, you need to arrange the numbers in ascending order and determine the middle value.
Arranged data set: 8, 9, 19, 28, 33, 37, 46
Since there is an odd number of values (7 in this case), the median will be the middle value.
Median = 28
Therefore, the median for the given data set is 28.
In the EAI sampling problem, the population mean is $51,800 and the population standard deviation is $4,000. When the sample size is n = 30, there is a .5034 probability of obtaining a sample mean within +/- $500 of the population mean. A. What is the probability that the sample mean is within $500 of the population mean if a sample of size 60 is used (to 4 decimals)?
B. What is the probability that the sample mean is within $500 of the population mean if a sample of size 120 is used (to 4 decimals)?
Answers
A) The probability that the sample mean is within $500 of the population mean for a sample of size 60 is 0.6611
B) The probability that the sample mean is within $500 of the population mean for a sample of size 120 is 0.7362
The EAI (Error of the Estimate) sampling problem is a specific case of the Central Limit Theorem, which states that the distribution of sample means from a population with a finite variance will be approximately normally distributed as the sample size increases.
The formula for calculating the standard error of the mean is
SE = σ/√n
where SE is the standard error, σ is the population standard deviation, and n is the sample size.
For n = 30, SE = 4,000/√30 = 729.16
A. For a sample size of n = 60, SE = 4,000/√60 = 516.40
To find the probability that the sample mean is within $500 of the population mean, we need to calculate the z-score for a range of +/- $500
z = (x - μ) / SE
where x is the sample mean, μ is the population mean, and SE is the standard error.
For a range of +/- $500, the z-scores are
z = ($51,300 - $51,800) / 516.40 = -0.969
z = ($52,300 - $51,800) / 516.40 = 0.969
Using a standard normal distribution table, the area between z = -0.969 and z = 0.969 is 0.6611.
B. For a sample size of n = 120, SE = 4,000/√120 = 368.93
Following the same steps as above, the z-scores for a range of +/- $500 are
z = ($51,300 - $51,800) / 368.93 = -1.364
z = ($52,300 - $51,800) / 368.93 = 1.364
Using the standard normal distribution table, the area between z = -1.364 and z = 1.364 is 0.7362.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
ill mark you brainiest , please help!!!
a boat measures 40m long and 10m wide.
a scale model of the boat measures 50cm long.
what is the scale factor of the model?
Answers
Step-by-step explanation:
50cm/40m = 0.5m/40m = 0.0125 = 1/80
Find the volume of the solid bounded by the cylinder x² + y² = 4 and the planes y + z = 4 and z = 0.
Answers
The volume of the solid bounded by the cylinder, y + z = 4, and z = 0 is 16π/7 cubic units.
To find the volume of the solid bounded by the cylinder x² + y² = 4, the planes y + z = 4, and z = 0, we can integrate the area of the cross-sections along the length of the cylinder.
Let's examine the cross-sections of the solid. The given cylinder x² + y² = 4 has a radius of 2 units. For each value of x, the cross-section is a circle with a radius of 2 - x² since it lies at a distance of x units from the y-axis. The center of this circle is at (x, y) = (x, 0). The plane y + z = 4 intersects this circle, forming a chord. The chord subtends an angle θ, where sin θ = (2 - x²)/2.
The length of the chord can be determined using the Pythagorean theorem: l = √(4 - (2 - x²)²) = √(4x² - x⁴) units.
Therefore, the area of the cross-section at a given x value is: A(x) = l(x)²π = πx²(4x² - x⁴)²/4.
Now, we can set up the integral to calculate the volume of the solid:
V = ∫(0 to 2) A(x) dx
= π/4 ∫(0 to 2) x²(4x² - x⁴)² dx
= π/4 ∫(0 to 2) (16x^6 - 32x^4 + 16x²) dx
= π/4 (2^7/7 - 2^6 + 2^3)
= 16π/7 cubic units.
Therefore, the volume of the solid bounded by the cylinder, y + z = 4, and z = 0 is 16π/7 cubic units.
To know more about Pythagorean theorem, click here
https://brainly.com/question/17179659
#SPJ11
If the length of a is 6, the length of b is 4, and the length of c is 7, what is the measure of angle B
Answers
Answer:
B = 34.77°
Step-by-step explanation:
For this problem you are given all three side lengths and asked to find an angle. To do this you can use the law of cosines which is written:
\(b^{2} =a^{2} +c^{2} -2ac Cos(B)\)
This can be rearranged to find the angle B:
\(b^{2} -a^{2} -c^{2} /-2ac = Cos(B)\)
With lowercase letters being sides and uppercase being angles.
We simply plug in the sides and solve:
\(4^{2} -6^{2} -7^{2}/-2*6*7= Cos(B)\)
0.8214 = Cos (B)
Then you use inverse cosine to get angle B alone.
B = 34.77°
Using two six-sided number cubes, each labeled with the numbers 1 through 6, event A is defined by rolling a sum greater than 8. Which of the following shows the
sample space of event A?
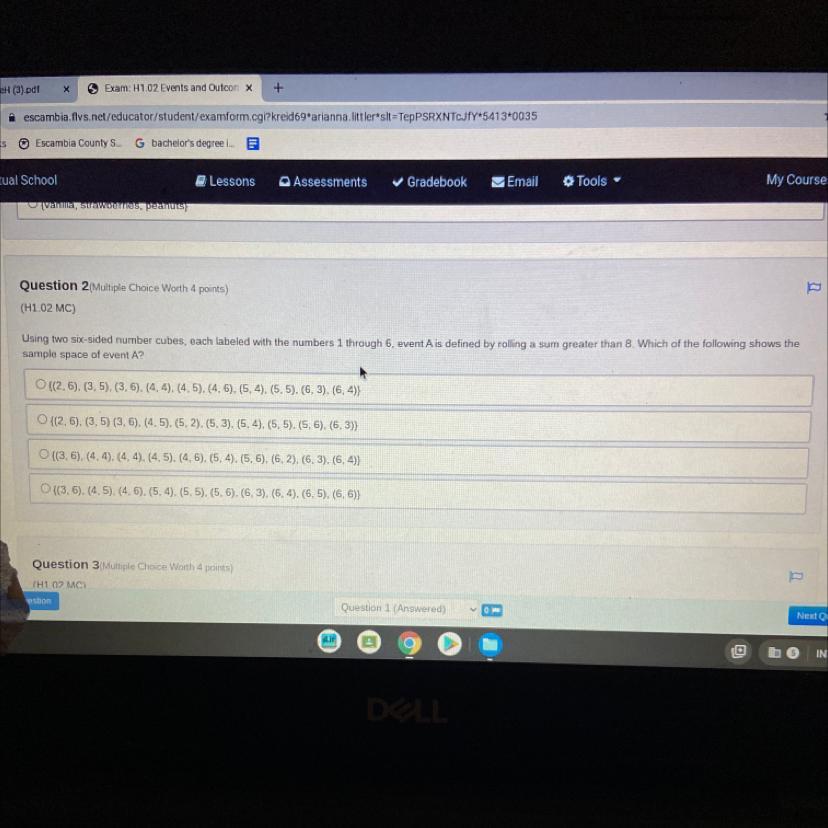
Answers
The sample space of event A would be {(3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}
What is a sample space for a random experiment?An experimenter does some random experiments which have a fixed set of outputs. That set of all possible outputs of that experiment is called sample space.
Using two six-sided number cubes, each labeled with the numbers 1 through 6.
Event A is defined by rolling a sum greater than 8.
Then the sample space of event A would be;
{(3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}
Learn more about sample space of a random experiment here:
https://brainly.com/question/9773761
#SPJ1
Answer:
{(3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}
proof in pic

what is the maximum number of edges in a directed graph without any self-loops, having a total 6 of vertices?
Answers
The maximum number of edges in a directed graph without any self-loops, having a total 6 of vertices is 15.
Edge:
In geometry, an edge is a particular type of line segment that connects two vertices of a polygon, polyhedron, or higher-dimensional polyhedron. In polygons, edges are line segments of the boundary and are often called polygon sides. In a polyhedron, or more generally a polytope, an edge is a line segment where two faces (or sides of a polyhedron) meet. A line segment connecting two vertices and passing inside or outside is called a diagonal, not an edge.
Directed graph:
A directed graph is a graph. A series of objects (called nodes or knots) connected together with all edges pointing from one node to another. A directed graph is sometimes called a directed graph or directed network. In contrast, graphs whose edges are bidirectional are called undirected graphs.
The graph containing maximum number of edge in a n node undirected graph without self loop is complete graph.
The number of edges in complete graph with n node, kₙ is
n(n − 1)/ 2
Now, based on the above formula:
n( n -1) /2
= 6( 6 - 1)/2
= 5× 6/2 = 30/2 = 15
Therefore, The maximum number of edges in a directed graph without any self-loops, having a total 6 of vertices is 15.
Learn more about Directed Graph:
https://brainly.com/question/15785278
#SPJ4
How do I simplify 2m=8-6m
Answers
Answer:
2m= 8-6m
2m+6m+=8-6m+6m let me know if this helps
Step-by-step explanation:
7.
Write the equation in point-slope form of the line that
passes through the given point and has the given slope.
(4,-7); m = -1/4
Answers
Answer:
Step-by-step explanation:
y + 7 = -1/4(x - 4)
y + 7 = -1/4x + 1
y = -1/4x - 6
Answer:
y+7=-1/4 (x-4)
Step-by-step explanation:
What value of x makes this statement true?
3.2 = 2x + 12
Answers
Answer:
-4.4
Step-by-step explanation:
Simplify (2a+5)6a^2
Can someone help please
Answers
Answer:
12a^3+30a^2
Step-by-step explanation:
6a^2(2a+5)
12a^3+30a^2
which mapping classification is most appropriate in mapping robbery locations over the last year to get a sense of the data distribution?
Answers
Mapping the locations of robberies over the last year is best done with a choropleth map. A choropleth map is a type of map that uses different colors to represent different levels of a given variable across a geographic area. This would be the most appropriate mapping classification for visualizing the data distribution of robbery locations.
Graduated Symbol Classification
Mapping classification that is most appropriate in mapping robbery locations over the last year to get a sense of the data distribution is Graduated Symbol Classification.What is mapping?Mapping is the creation of maps, which are graphical representations of the Earth's surface or other physical entities. Mapping has many benefits in today's society, including in the areas of spatial analysis, cartography, and geographic information systems. Different types of maps can be created based on the goals of the cartographer, such as topographic maps, road maps, and weather maps.Graduated Symbol Classification:Graduated Symbol Classification is a technique in which different symbol sizes are utilized to represent different feature values of a specific thematic map variable. In this type of classification, the variable is divided into a few groups or classes, with each class having a specific range of values. The same symbol is used to indicate each class, but its size varies depending on the value of the variable.A graduated symbol map, in which a variety of symbols are used to represent different feature values, is one of the most efficient ways to display quantitative data. Graduated symbols are most commonly utilized for the following thematic maps: population density, magnitude of an earthquake, or frequency of an event.
Learn more about mapping
brainly.com/question/24267908
#SPJ11
Which expression represents the phrase 5+ the quotient of 12. 8 and 3. 2
Answers
Expression 5 + (12.8 ÷ 3.2) represents the phrase 5 + the quotient of 12. 8 and 3. 2 and option (a) is the correct answer.
Expressions refer to a phrase with at least two numbers or variables with any mathematical operations such as addition, exponents, etc. x - 6, 9 + 4y, and 6a are all examples of mathematical expressions.
Equations refer to a sentence when two expressions are equated with the help of '='. x - 6 = 6a is an example of an equation.
In phrase 5+ the quotient of 12. 8 and 3. 2
We divide the phrase into different mathematical operations.
The first operation is of addition with 5, we can write the beginning as 5 + ...
The next operation is division in the phrase the quotient of 12. 8 and 3. 2 which is added to the expression and we get 5 + (12.8 ÷ 3.2)
And we get our answer.
Learn more about Expressions:
https://brainly.com/question/25968875
#SPJ4
The complete question might be :
Which expression represents the phrase 5+ the quotient of 12. 8 and 3. 2?
a. 5 + (12.8 ÷ 3.2)
b. 5 - (12.8 + 3.2)
c. 5 + (12.8 * 3.2)
d. none of the above
The surface area of a cube is represented by the expression below, where s is the side length of the cube. Find the surface area of a cube-shaped jewelry gift box with a side length of 9 centimeters.
Answers
Answer:
486 centimeters³
Step-by-step explanation:
Surface area of a cube = 6s²
Where,
s = side length
Find the surface area of a cube-shaped jewelry gift box with a side length of 9 centimeters.
s = 9 centimeters
Surface area of a cube = 6s²
= 6 × 9²
= 6 × 81
= 486 centimeters³
Surface area of a cube-shaped jewelry gift box with a side length of 9 centimeters 486 centimeters³
Fallacies of relevance
I need to describe a time a work I used fallacies of relevance
please help..
Answers
Fallacies of relevance are types of logical fallacies that occur when an argument is presented without a relevant connection to the subject matter.
Rather than addressing the topic, these fallacies are aimed at the listener's feelings, emotions, or biases.There are many different types of fallacies of relevance, but some of the most common are ad hominem, straw man, appeal to authority, and red herring. Ad hominem, for example, is a type of fallacy that attacks the speaker rather than addressing the argument they are presenting.. It can undermine the quality of your argument and make you seem less credible.
However, if you want to describe a time when you used these fallacies, you might think back to a situation where you were arguing with someone and felt like you were losing the argument. In this case, you might have resorted to a fallacy of relevance to try to regain control of the conversation. In conclusion, it is important to avoid using fallacies of relevance in your arguments. Instead, focus on addressing the topic at hand and presenting logical, evidence-based arguments.
To know more about Fallacies visit:
brainly.com/question/32112262
#SPJ11
For 91-92; A dental surgery has two operation rooms. The service times are assumed to be independent, exponentially distributed with mean 15 minutes. Andrew arrives when both operation rooms are empty. Bob arrives 10 minutes later while Andrew is still under medical treatment. Another 20 minutes later Caroline arrives and both Andrew and Bob are still under treatment. No other patient arrives during this 30-minute interval. 91. What is the probability that Caroline will be ready before Andrew? A. 0.35 B. 0.25 C. 0.52 D. None of these 92. What is the probability that Caroline will be ready before Bob? A. 0.35 B. 0.25 C. 0.52
Answers
Answer:
91. The probability that Caroline will be ready before Andrew is 0.25 (Option B). Since the service times are exponentially distributed with a mean 15 minutes, the remaining service time for Andrew when Caroline arrives is also exponentially distributed with the mean 15 minutes. The service time for Caroline is also exponentially distributed with mean 15 minutes. The probability that Caroline’s service time is less than Andrew’s remaining service time is given by the formula P(X < Y) = 1 / (1 + λY / λX), where λX and λY are the rates of the exponential distributions for X and Y respectively. Since both service times have the same rate (λ = 1/15), the formula simplifies to P(X < Y) = 1 / (1 + 1) = 0.5. Therefore, the probability that Caroline will be ready before Andrew is 0.25.
92. The probability that Caroline will be ready before Bob is 0.35 (Option A). Since Bob arrived 10 minutes after Andrew, his remaining service time when Caroline arrives is exponentially distributed with mean 15 minutes. Using the same formula as above, we get P(X < Y) = 1 / (1 + λY / λX) = 1 / (1 + 1) = 0.5. Therefore, the probability that Caroline will be ready before Bob is 0.35.
-2.3c-6.6=-12.2-3. solve for me please ( show work )
Answers
Answer:
c = 3.73913043
Step-by-step explanation:
Subtract 3 from - 12.2
Move all terms not containing c to the right side of the equation.
− 2.3 c = − 8.6
Divide each term in − 2.3 c = − 8.6 by − 2.3 and simplify.
If a point is randomly chosen on the regular hexagon shown, what is the probability that it will be in a green section of the figure?
1/6
1/3
1/2
3/4

Answers
Answer:
1/2
Step-by-step explanation:
i just took the test on usatestprep
Answer:
1/2
Step-by-step explanation:
two dice are rolled, one blue and one red. how many outcomes have either the blue die 3 or an even sum or both?
Answers
There are 25 possible outcomes where we either get a blue die 3 or an even sum or both.
To solve this problem, we need to use the concept of probability. Probability is the likelihood of an event occurring, expressed as a number between 0 and 1. In this case, we want to find the probability of rolling either a blue die 3 or an even sum or both.
First, let's count the number of outcomes where the blue die is 3. There is only one way to get a 3 on the blue die, and the red die can be any number from 1 to 6. Therefore, there are 6 possible outcomes where the blue die is 3.
Next, let's count the number of outcomes where we get an even sum. There are three ways to get an even sum: (1,1), (2,2), and (3,3). For each of these outcomes, the blue die can be any number from 1 to 6. Therefore, there are 18 possible outcomes where we get an even sum.
Finally, let's count the number of outcomes where we get both a blue die 3 and an even sum. There is only one way to get a blue die 3 and an even sum: (3,3). Therefore, there is only one possible outcome where we get both a blue die 3 and an even sum.
To find the total number of outcomes that have either a blue die 3 or an even sum or both, we need to add the number of outcomes where the blue die is 3, the number of outcomes where we get an even sum, and the number of outcomes where we get both. This gives us:
6 + 18 + 1 = 25
Therefore, there are 25 possible outcomes where we either get a blue die 3 or an even sum or both.
Learn more about probability brainly.com/question/30034780
#SPJ11
Simplify the expression:
-3(3-4x) =
Answers
Answer:
- 9 + 12x
Step-by-step explanation:
- 3(3 - 4x) ← multiply each term in the parenthesis by - 3
= - 9 + 12x
You and a group of friends participate in a game where you must use clues to escape from a room. You have a limited amount of time to escape and are allowed 3 free clues. Additional clues may be requested, but each removes 5 minutes from your remaining time. What integer represents the total change in the time when you use 5 clues?
Answers
Answer:
The integer that represent the total change in time when 5 clues are used is 10
Step-by-step explanation:
The given parameters are;
The number of free clues available = 3
The number of minutes removed for an additional clue = 5 minutes
Therefore, the total change in time when 5 clues are used is given as follows;
The number of free clues available 3
The number of clues for which 5 minutes is removed from the remaining time when 5 clues are selected = 5 - 3 = 2 clues
Therefore, the total change in time = The number additional clues × 5 minutes/clue
The total change in time = 2 clues × 5 minutes/clue = 10 minutes
The total change in time = 10 minutes
Therefore, the integer that represent the total change in time (in minutes) when 5 clues are used = 10.
Answer:
-10
Step-by-step explanation: