PLEASE SOLVE STEP BY STEP
Solve bx − 4=5 for x. Assume that b≠0.
Multiple choice question.
A)
x=1b
B)
x=9b
C)
x=9 – b
D)
x=1 – b
Answers
Answer:
x=9b
Step-by-step explanation:
The value of x for the expression will be equal to 9 / b.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given expression is bx − 4=5, the value of x will be calculated as,
bx − 4=5
bx = 5 + 4
bx = 9
x = 9 / b
Therefore, the value of x for the expression will be equal to 9 / b.
To know more about an expression follow
https://brainly.com/question/25968875
#SPJ2
Related Questions
Peter enrolled $80,000 worth of debt with National Debt Relief. Peter’s fee for the service is 20% of the enrolled debt. How much is Peter’s fee?*
Answers
Answer:
16000
Step-by-step explanation:
Verify that (cos²a) (2 + tan² a) = 2 - sin² a....
Answers
Trigonometric Formula's:
\(\boxed{\sf \ \sf \sin^2 \theta + \cos^2 \theta = 1}\)
\(\boxed{ \sf tan\theta = \frac{sin\theta}{cos\theta} }\)
Given to verify the following:
\(\bf (cos^2a) (2 + tan^2 a) = 2 - sin^2 a\)
\(\texttt{\underline{rewrite the equation}:}\)
\(\rightarrow \sf (cos^2a) (2 + \dfrac{sin^2 a}{cos^2 a} )\)
\(\texttt{\underline{apply distributive method}:}\)
\(\rightarrow \sf 2 (cos^2a) + (\dfrac{sin^2 a}{cos^2 a} ) (cos^2a)\)
\(\texttt{\underline{simplify the following}:}\)
\(\rightarrow \sf 2cos^2 a + sin^2 a\)
\(\texttt{\underline{rewrite the equation}:}\)
\(\rightarrow \sf 2(1 - sin^2a ) + sin^2 a\)
\(\texttt{\underline{distribute inside the parenthesis}:}\)
\(\rightarrow \sf 2 - 2sin^2a + sin^2 a\)
\(\texttt{\underline{simplify the following}} :\)
\(\rightarrow \sf 2 - sin^2a\)
Hence, verified the trigonometric identity.
Answer:
See below ~
Step-by-step explanation:
Identities used :
⇒ cos²a = 1 - sin²a
⇒ tan²a = sin²a / cos²a
============================================================
Solving :
⇒ (cos²a) (2 + tan² a)
⇒ 2cos²a + (cos²a)(tan²a)
⇒ 2(1 - sin²a) + sin²a
⇒ 2 - 2sin²a + sin²a
⇒ 2 - sin²a [∴ Proved √]
I put the question in the photo but it’s basically a contingency table I just can’t find which like formula to us

Answers
a) The probability that exactly one of them will be a girl = 0.3407
b) The probability that at least one of them will like the football = 0.7672
a) If we select three students then the probability that exactly one of them will be a girl
From the attached two way table we can observe that the total number of girls = 22
the total number of boys = 18
and the total number of students = 40
The possible outcomes for selecting 3 students from 40 would be,
⁴⁰C₃
Using combination formula,
⁴⁰C₃ = 40! / (3! × (40 - 3)!)
= 9880
If there is exactly one girl then other two must be boys in the set of 3 selected students.
So, the required probability would be,
P = (²²C₁ × ¹⁸C₂) / ⁴⁰C₃
P = (22 × 153)/9880
P = 0.3407
b) The number of students like the football = 15
and the number of students who don't like the football are 40 - 15 = 25
The probability that at least one of them will like the football would be,
P = (¹⁵C₃ × ²⁵C₀ + ¹⁵C₂ × ²⁵C₁ + ¹⁵C₁ × ²⁵C₂) / ⁴⁰C₃
P = ((455 × 1) + (105 × 25) + (15 × 300)) / 9880
P = 0.7672
Learn more about the probability here:
https://brainly.com/question/15124899
#SPJ1
I need help again this making so tried so help me pls I beg I want to sleep

Answers
Answer:
32229 feetStep-by-step explanation:
The high and low points are
31098 feet- 1131 feetThe difference in elevation is:
31098 - (-1131) = 32229 feetStep-by-step explanation:
Answer:
32229 feet
Step-by-step explanation:
The high and low points are
31098 feet - 1131 feet
The difference in elevation is:
31098 - (-1131) = 32229 feet
Hope it will help you in your need
Put the following equation of a Lin slope-intercept form, simplifying all fractions 6x+4y=4

Answers
The slope-intercept form is given by:
\(y=mx+b\)Therefore, to find this form, we need to solve for y the given equation:
\(6x+4y=4\)Subtract both sides 6x:
\(6x-6x+4y=4-6x\)\(4y=4-6x\)Now, divide both sides by 4:
\(\frac{4y}{4}=\frac{4-6x}{4}\)Simplify the expression:
\(y=\frac{4}{4}-\frac{6x}{4}\)\(y=1-\frac{3x}{2}\)We can rewrite the equation as:
\(y=-\frac{3x}{2}+1\)Where -3/2 represents the slope and 1 represents the y-intercept.
permieter of 2 rectangles is 54 cm.
work out the area of a square
Answers
The Area of Square is 81 cm².
let the side of the square which is length for both rectangles be a.
let the width of rectangle be x and y.
So, x+ y= a
sum of perimeters= 54
2 (a +x ) + 2 (a+ y) = 54
2a+ 2x + 2a+ 2y = 54
2a + 2a + 2(x+ y) = 54
4a + 2 (a) = 54
4a + 2a = 54
6a = 54
a= 54/6
a= 9
So, area of square
= 9 x 9
= 81 cm²
Learn more about Area here:
https://brainly.com/question/1631786
#SPJ1
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
The flight of a golf ball can be represented by a parabola with a vertex (75,55). During the flight, the ball was 100 yards away from the tee and had a height of 49.375 feet. What is the equation in vertex for a parabola that represents the ball's vertical distance, y, and horizontal distance from the tee, x?
Answers
The equation in vertex for the parabola for y in terms of x is y = -0.009(x - 75)² + 55
How to determine the equation in vertex for a parabola?From the question, we have the following parameters that can be used in our computation:
Vertex = (75, 55)
Point = (100, 49.375)
The equation in vertex form for a parabola is represented as
y = a(x - h)² + k
Where
Vertex (h, k) = (75, 55)
Point (x, y) = (100, 49.375)
So, we have
y = a(x - 75)² + 55
Substitute (x, y) = (100, 49.375) in y = a(x - 75)² + 55
49.375 = a(100 - 75)² + 55
So, we have
625a = -5.625
Divide by 625
a = -0.009
Substitute a = -0.009 in y = a(x - 75)² + 55
y = -0.009(x - 75)² + 55
Hence, the equation is y = -0.009(x - 75)² + 55
Read more about parabola at
https://brainly.com/question/1480401
#SPJ1
Baby otters born 3/4 of a month early at birth of the week was 78 kg which is 9/10 kg less than the average weight of a newborn otter in the aquarium. What is the average weight of a newborn otter?
Answers
Answer:
Step-by-step explanation:
Baby otter is 9/10 kg less than the average.
Determine the equation of the ellipse with foci... Please put the dots on the graph thats in the image. 100 points

Answers
Answer:
\(\frac{(x-7)^2}{8^2} + \frac{(y-2)^2}{17^2} = 1\)
Step-by-step explanation:
Major axis length 2a
⇒ 2a = 34
⇒ a = 34/2
⇒ a = 17
General eq of ellipse:
\(\frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1\)
centre : (h,k)
foci: (h, k+c) and (h,k-c)
Gn. foci : (7, 17) and (7, -13)
Comparing the above 2 lines,
h = 7,
k + c = 17 -eq(1)
k - c = -13 -eq(2)
eq(1) + eq(2):
(k + c) + (k - c) = 17 + (-13)
2k = 4
k = 2
sun k = 2 in eq(1):
2 + c = 17
c = 15
Also, c² = a² - b²
b² = a² - c²
= 17² - 15²
= 64
b² = 8²
b = 8
substituting in ellipse eq,
\(\frac{(x-7)^2}{8^2} + \frac{(y-2)^2}{17^2} = 1\)

Answer:
\(\dfrac{(x-7)^2}{64}+\dfrac{(y-2)^2}{289}=1\)
Step-by-step explanation:
As the foci of the ellipse have the same x-value, the ellipse is vertical.
The formula for a vertical ellipse is:
\(\boxed{\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1}\)
where:
b > ab is the major radius and 2b is the major axis.a is the minor radius and 2a is the minor axis.Center = (h, k)Vertices = (h, k±b)Co-vertices = (h±a, k)Foci = (h, k±c) where c² = b² - a²Given the major axis is 34:
2b = 34b = 17b² = 289The center of an ellipse is located at the midpoint between its two foci.
Given the foci are (7, 17) and (7, -13), the center of the ellipse is:
\((h, k) = (7, 2)\)
As the formula for the foci is (h, k±c), then (k, h±c) = (7, 2±c). Therefore:
\(\begin{aligned}2\pm c &= 17, -13\\\pm c &= 15, -15\\c &= 15\end{aligned}\)
The vertices are:
\(\begin{aligned}(h, k\pm b) &= (7, 2 \pm 17)\\& = (7, 19) \; \textsf{and}\; (7, -15)\end{aligned}\)
To find the value of a, substitute the values of b and c into c² = b² - a²:
\(\begin{aligned}c^2&=b^2-a^2\\15^2&=17^2-a^2\\a^2&=\sqrt{17^2-15^2}\\a^2&=64\\a&=8\end{aligned}\)
The co-vertices are:
\(\begin{aligned}(h \pm a, k) &= (7 \pm 8, 2)\\& = (-1,2) \; \textsf{and}\; (15,2)\end{aligned}\)
Therefore:
a = 8 ⇒ a² = 64b = 17 ⇒ b² = 289h = 7k = 2To find the equation of the ellipse, substitute these values into the formula:
\(\boxed{\dfrac{(x-7)^2}{64}+\dfrac{(y-2)^2}{289}=1}\)
Major axis, 2b = 34Minors axis, 2a = 16Center = (7, 2)Vertices = (7, -15) and (7, 19)Co-vertices = (-1, 2) and (15, 2)Foci = (7, 17) and (7, -13)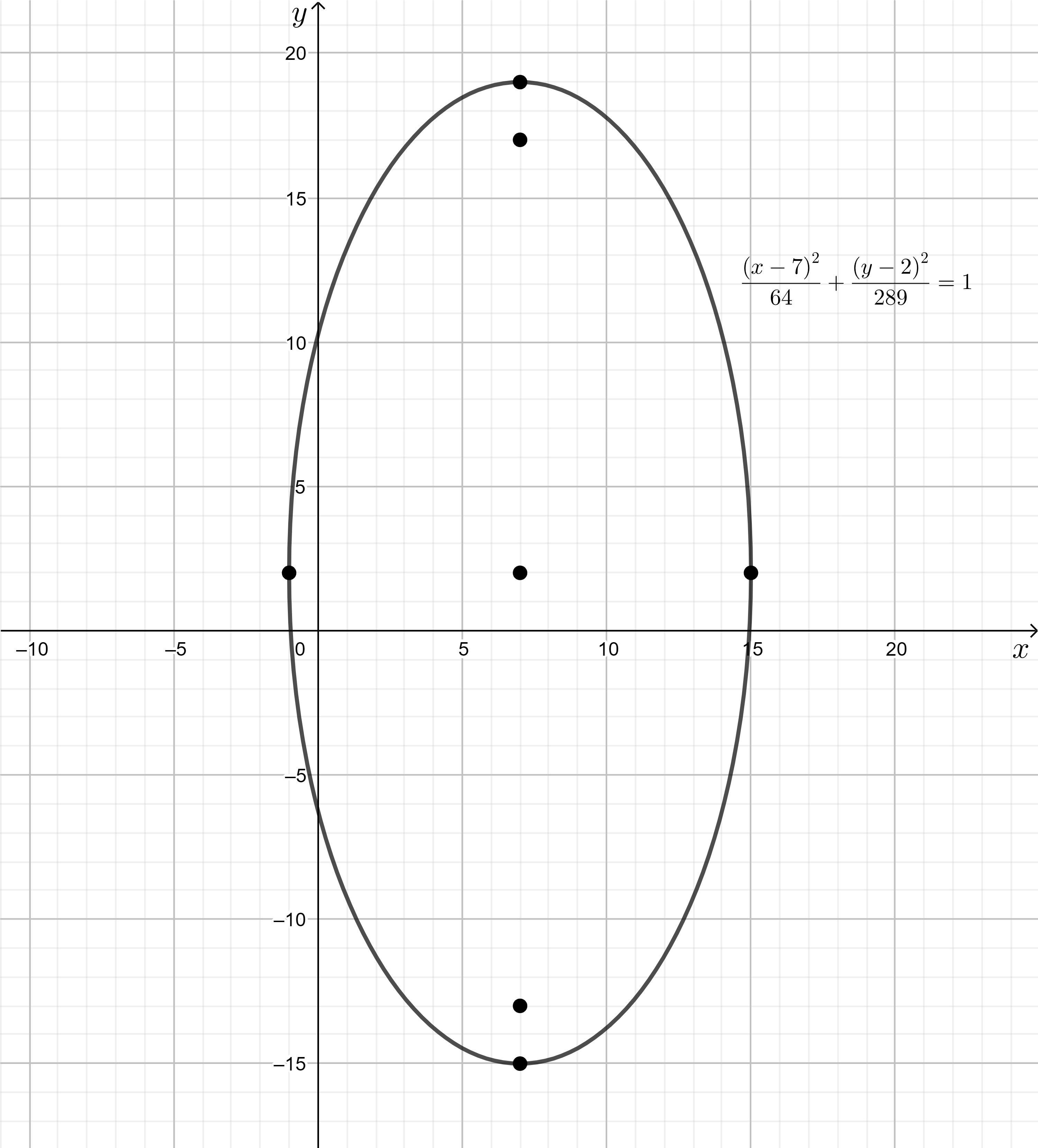

There is a stack of logs in the backyard. There are 15 logs in the 1st layer, 14 in the second, 13 in the third, 12 in the fourth, and so on with the last layer having one log. How many logs are in the stack?
Answers
I think the answer is 54.
Is. She analyzes
st.
Martha graphs the data for the number of bracelets made, a, and the number of beads used,
y, and draws a line through the points.
Number of Beads Used
600
500
400
300
200
100
0
Bracelets Made
versus Beads Used
(31, 651)
(23, 483).
(10, 210)
5 10 15 20 25 30 35
Number of Bracelets Made
Write an equation that represents the relationship between the number of bracelets made
and the number of beads used. Show or explain how you found the slope and y-intercept.
Enter your equation and your work or explanation in the space provided.
You may use the drawing box to add a drawing to help explain your answer.
A
7
44
▶
Exhibits
P
Answers
The equation for the relationship between the number of bracelets made and the number of beads is y = 21x.
First, the rate of change
= (483 - 210) / (23 - 10)
= 273 / 13
= 21
So, the equation for the relationship between the number of bracelets made and the number of beads used.
(y - 210) = 21 (x- 10)
y - 210 = 21x - 210
y = 21x
Learn more about Slope here:
https://brainly.com/question/3605446
#SPJ1
Check all the statements) that are true about the polynomial function graphed
Its leading coefficient is positive. its leading coefficient is negative.
It has an odd degree
It has an even degree
It has exactlv two real zeroes
It has exactly three real zeroes.
None of the zeroes have even multiplicity
None of the zeroes have odd multiplicity.
Answers
The true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
From the given options, the true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
Let's analyze each statement:
Its leading coefficient is positive:
The leading coefficient of a polynomial is the coefficient of the term with the highest degree.
From the graph, if the polynomial is going upwards on the right side, it indicates that the leading coefficient is positive.
It has an odd degree: The degree of a polynomial is the highest power of the variable in the polynomial expression.
If the graph has an odd number of "turns" or "bumps," it indicates that the polynomial has an odd degree.
None of the zeroes have even multiplicity:
The multiplicity of a zero refers to the number of times it appears as a factor in the polynomial.
In the given graph, if there are no repeated x-intercepts or no points where the graph touches and stays on the x-axis, it implies that none of the zeroes have even multiplicity.
The other statements (its leading coefficient is negative, it has an even degree, it has exactly two real zeroes, it has exactly three real zeroes, and none of the zeroes have odd multiplicity) cannot be determined based solely on the information given.
Therefore, the true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
For similar question on polynomial function.
https://brainly.com/question/31528136
#SPJ8
What is the median?

Answers
the median is the middle number in a sorted, ascending or descending, list of numbers, i like to think of it as "middle"
The Chess club and the Robotics team both meet in the school gym. The chess club meets every six days. The Robotics team meets every eight days They are sharing the gym today. In how many days will they share the gym again?
Answers
Answer: 24 days
Step-by-step explanation:
The number of days from now when the chess club will be in the gym:
6, 12, 18, 24, 30, 36, ...
The number of days from now when the robotics team will be there:
8, 16, 24, 32, 40, 48, ...
The lowest number they have in common is 24 days.
A more algebraic way to look at this (which is what your instructor probably wants) is to find the smallest whole number that is divisible by 6 and also divisible by 8.
The prime factorization of 6 is 2*3
The prime factorization of 8 is 2*2*2
The smallest whole number divisible by 6 and by 8 must have all the prime factors but no more than that.
For the factor of 2, the number 6 has one of them and 8 has three of them , so we need the highest number of factors for just one of the numbers --> 3 factors of 2 (We don't add the 3 factors from 8 and the one factor from 6 to get 4 factors. That would be incorrect.)
For the factor of 3, it only appears as a factor of 6 and it only appears once --> one factor of 3.
So, we need 2 * 2 * 2 * 3 = 24
I hope this helps.
Kaitlyn is walking on a treadmill at a constant pace for 28 minutes. She has programmed the treadmill for a 2-mile walk. The display counts backward to show the distance remaining. Enter and graph the equation that gives the distance f(x) left in miles as a function of the number x of minutes she has been walking. Then, find and compete the interpretation of the x- and y-intercepts.
Answers
What is the axis of symmetry of the
parabola graphed below?
O x=4
Oy=2
Oy=4
Ox=2
Other:

Answers
Answer:
A
Step-by-step explanation:
i think so..sorry if im wrong
the amounts of time employees of a telecommunications company have worked for the company are normally distributed with a mean of 5.4 years and a standard deviation of 2.1 years. random samples of size 12 are drawn from the population and the mean of each sample is determined.
O 5.4 years, 0.48 years O 5.4 years, 0.10 years O 1.18 years, 2.2 years
O 1.18 years, 0.48 years
Answers
Using statistics we know that the mean value is 5.6 years, and the standard error is 0.4478.
What are statistics?The gathering, characterization, analysis, and drawing of inferences from quantitative data are all tasks that fall under the purview of statistics, a subfield of applied mathematics.
Probability theory, linear algebra, and differential and integral calculus play major roles in the mathematical theories underlying statistics.
So, we have:
μ = 5.6
σ = 1.9
n = 18
Figuring out each sample's mean:
Therefore, the population means itself serves as the best estimator of the sample mean.
μₓ = μ = 5.6
The sample mean is 5.6 years as a result.
Estimating the standard deviation:
By using the formula:
Standard error = σ/√n
Given that the samples are of size n = 18 and the standard deviation is = 1.9:
Standard error = 1.9/√18 = 0.4478
Therefore, using statistics we know that the mean value is 5.6 years, and the standard error is 0.4478.
Know more about statistics here:
https://brainly.com/question/15525560
#SPJ4
Complete question:
The amount of time employees of a telecommunications company have worked for the company is normally distributed with a mean of 5.6 years and a standard deviation of 1.9 years. Random samples of size 18 are drawn from the population and the mean of each sample is determined. Find the mean and the standard error.
Find z within the problem.

Answers
Answer:
z = √35
Step-by-step explanation:
In this geometry, all of the right triangles are similar, so corresponding sides are proportional.
long side / hypotenuse = 5/z = z/(2+5)
z² = 5(7) = 35
z = √35
Four different stores have sales on the same stickers.
Which deal gives the customer the best price per sticker?
A. 2 stickers for 25 cents
B. 3 stickers for 39 cents
c. 4 stickers for 80 cents
D. 5 stickers for 63 cents
Answers
39/3=13
80/4=20
63/5= 12.6
since the lowest one is 12.5 and is for 25/2 the answer is A
What is the equation of a line that has a slope of - 1/2 and a y intercept of 3
Answers
y = ½x +3
Step-by-step explanation:
Slope = m = ½
y-intercept = 3
Substitute values into Slope intercept form :
\(y = mx + b\)
Where m = slope
b = y intercept
\(y = \frac{1}{2} x + 3\)
Please help i'll mark brainliest

Answers
Answer:
it issssss sass ccccccccccccccccccc
La empresa clarisse dedicada al rubro de telefónica, está ampliando su cobertura, debido a esto está colocando postes, donde la séptima parte de un poste está enterrada, y sobresale del suelo 25 metros. Calcular la altura del poste aproximado a los centímetros.
Answers
The approximate height of the pole in centimeters is 17,500 centimeters.
We have,
Let's start by calculating the total length of the pole, which is buried plus the part that protrudes from the ground.
We know that the part that protrudes is 25 meters and that it represents one-seventh of the total length.
25 = L/7
where L is the total length of the pole.
We can solve for L by multiplying both sides of the equation by 7:
L = 7 x 25
= 175 meters
Now we need to convert this length to centimeters.
Since 1 meter is equal to 100 centimeters,
175 meters x 100
= 17,500 centimeters
Therefore,
The approximate height of the pole in centimeters is 17,500 centimeters.
Learn more about unit conversion here:
https://brainly.com/question/13899873
#SPJ1
The complete question.
The Clarisse company, dedicated to the telephone business, is expanding its coverage, due to this, it is placing poles, where the seventh part of a pole is buried, and protrudes 25 meters from the ground. Calculate the approximate height of the pole in centimeters.
For the arithmetic sequence beginning with the terms {-1, 2, 5, 8, 11, 14...}, what is the sum of the first 16 terms?
Answers
Answer:
S₁₆ = 344
Step-by-step explanation:
the sum to n terms of an arithmetic sequence is
\(S_{n}\) = \(\frac{n}{2}\) [ 2a₁ + (n - 1)d ]
where a₁ is the first term and d the common difference
here a₁ = - 1 and d = a₂ - a₁ = 2 - (- 1) = 2 + 1 = 3 , then
S₁₆ = \(\frac{16}{2}\) [ (2 × - 1) + (15 × 3) ]
= 8 (- 2 + 45)
= 8 × 43
= 344
pls complete these two questions! 80 points!!

Answers
3a. An equation in slope-point for this line is y + 2 = 1/2(x - 0).
3b. The equation in slope-intercept form is y = 1/2(x) - 2.
4a. An equation in slope-point form to represent this function is y - 3875 = -1/695(x - 19375).
4b. The cost of operating a car that has been driven 31250 km is $3892.086.
How to determine an equation of this line?In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):
y - y₁ = m(x - x₁)
Where:
x and y represent the data points.m represent the slope.Part 3.
First of all, we would determine the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (0 + 2)/(4 - 0)
Slope (m) = 1/2
At data point (0, -2) and a slope of 1/2, a linear equation in slope-intercept form for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y + 2 = 1/2(x - 0)
y = 1/2(x) - 2
Part 4a.
Based on the information provided about Jay's business, we would determine the slope of the line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (3900 - 3875)/(2000 - 19375)
Slope (m) = 25/-17375
Slope (m) = -1/695
At data point (19375, 3875) and a slope of -1/695, a linear equation in slope-intercept form for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - 3875 = -1/695(x - 19375)
Part 4b.
For the cost when x = 31250 km, we have:
y - 3875 = -1/695(31250 - 19375)
y = 17.086 + 3875
y = $3892.086.
Read more on point-slope here: brainly.com/question/24907633
#SPJ1
cos 90 - 2sin45 + 2tan180
Answers
Answer:
- \(\sqrt{2}\)
Step-by-step explanation:
cos90° - 2sin45° + 2tan180°
= 0 - ( 2 × \(\frac{\sqrt{2} }{2}\) ) + 2(0)
= 0 - \(\sqrt{2}\) + 0
= - \(\sqrt{2}\)
A large flagpole stands outside of an office building. Marquis realizes that when he looks up from the ground, 60m away from the flagpole, and the top of the building line up. If the flagpole is 35m tall, and Marquis is 170m from the building, how tall is the building?
Answers
Answer:
99.166666666666666666666; 595/6; 99 1/6; 99
Step-by-step explanation:
THE FORMULA IS (x)/(170)=(35)/(60)
solve for x
copy the formula in bold and paste it to math w]y:
(x)/(170)=(35)/(60)
choose the option to solve for x and 99.666666666666∞ is the answer.
Solve these equations. |x+1/2|=3 2/3
Answers
Answer:
Step-by-step explanation:
|x+a|=b
x+a=±b
x=a±b
x=a+b
and x=a-b
Evaluate squareroot of
61.73²-38.27²
Answers
Answer:
48.43552415324934
Step-by-step explanation:
61.73²-38.27² = 2346
\(\sqrt{2346}\) = 48.43552415324934
kindly check if it’s correct and correct those that are wrong. thank you! as well as calculations
The following information is known for the month of December:
1. Purchases of supplies for cash during December were $3,300. Supplies on hand at the end of December equal $2,900.
2. No insurance payments are made in December. Insurance expired in December is $1,400.
3. November salaries payable of $9,800 were paid to employees in December. Additional salaries for December owed at the end of
the year are $14,800.
View transaction list
4. On December 1, Golden Eagle received $2,700 from a customer for rent for the period December through February. By the end of
December, one month of rent has been provided.
Required:
For each item, (a) record any transaction during the month of December, and (b) prepare the related December 31 year-end adjusting
entry. (If no entry is required for a particular transaction/event, select "No Journal Entry Required" in the first account field.)
no random answers ty!

Answers
Correction in point 1: Purchases of supplies for cash during December were $3,300. Supplies on hand at the end of December equal $2,800.
What is Journal Entry?
The act of recording any economic transactions is called a journal entry. An accounting journal lists transactions and displays a company's debit and credit balances. Each recording in the journal entry can be either a debit or a credit, and it can be made up of multiple recordings. The way an accounting transaction is entered into a company's accounting records is through an accounting journal entry.
This question is related to the account and finance subject.
To know more about journal entry, visit:
https://brainly.com/question/28390337
#SPJ1