PLEASE I will be your best friend lol just please help me !!! 10 points
factor the polynomial: -x^3-2x^2-3x
Answers
Answer: I believe your answer is
-x(1^3+2x+3)
Step-by-step explanation:
Related Questions
Find the total differential of the function: \[ Z=\left(2 x_{1}+3\right)\left(x_{2}+9\right) \]
Answers
The total differential of the function \(\(Z = (2x_1 + 3)(x_2 + 9)\)\) is given by:
\(\[\mathrm{d}Z = \frac{\partial Z}{\partial x_1}\mathrm{d}x_1 + \frac{\partial Z}{\partial x_2}\mathrm{d}x_2\]\)
To calculate the total differential, we need to find the partial derivatives of Z with respect to \(\(x_1\)\) and \(\(x_2\)\). Taking the partial derivative of Z with respect to \(\(x_1\)\) while treating \(\(x_2\)\) as a constant, we get:
\(\[\frac{\partial Z}{\partial x_1} = 2(x_2 + 9)\]\)
Next, taking the partial derivative of Z with respect to \(\(x_2\)\) while treating \(\(x_1\)\) as a constant, we have:
\(\[\frac{\partial Z}{\partial x_2} = 2x_1 + 3\]\)
Substituting these partial derivatives into the total differential equation, we get:
\(\[\mathrm{d}Z = (2(x_2 + 9))\mathrm{d}x_1 + (2x_1 + 3)\mathrm{d}x_2\]\)
Therefore, the total differential of the function Z is:
\(\[\mathrm{d}Z = (2(x_2 + 9))\mathrm{d}x_1 + (2x_1 + 3)\mathrm{d}x_2\]\)
To know more about partial derivatives and total differentials, refer here:
https://brainly.com/question/31402354#
#SPJ11
Graph the equation 4x+8y=16

Answers
Move the 4x to the other side to put it into slope intercept form.
8y=-4x+16
Then divide by 8.
Y=-1/2x+2
The slope is -1/2 and the Y intercept is 2.

Answer:
4x+8y=16
8y=4x+16
4/8. 16/8
y=1/2x+2
PLEASE ANSWER CORRECTLY! I WILL MARK BRAINLIEST! I really need an answer!
Dashawn solves the following system of equations using the elimination method.
3x−4y=36
5x+2y=8
What value does he correctly determine for x?
Enter you answer in the box.
x =
Answers
In a recent election, 63% of all registered voters participated in voting. In a survey of 275 retired voters, 162 participated in voting. Which is higher, the population proportion who participated or the sample proportion from this survey?
Answers
The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.
The population proportion who participated in voting is given as 63% of all registered voters.
This means that out of every 100 registered voters, 63 participated in voting.
In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.
Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .
Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.
It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.
For similar question on population proportion.
https://brainly.com/question/29516589
#SPJ8
A landscaper buried a water line around a rectangular lawn to serve as a supply line for a sprinkler system. The length of the lawn is 6 times its width. If 630 feet of pipe was used to do the job, what is the length and the width of the lawn
Answers
Answers:
Length = 270 feet
Width = 45 feet
========================================================
Work Shown:
x = width
6x = length, since it is 6 times the width
P = perimeter of rectangle
P = 2*(Length + Width)
P = 2*(6x + x)
P = 2*(7x)
P = 14x
Plug in the given perimeter P = 630 and solve for x.
P = 14x
14x = P
14x = 630
x = 630/14
x = 45
The width is 45 feet.
The length must be 6x = 6*45 = 270 feet.
The required length and width of the lawn is given as Length = 270 feet and Width = 45 feet.
Given that,
A landscaper buried a water line around a rectangular lawn to serve as a supply line for a sprinkler system. The length of the lawn is 6 times its width. If 630 feet of pipe was used to do the job, what is the length and the width of the lawn is to be determined.
Perimeter is the measure of the figure on its circumference.
Here,
let the length be l and the width be w,
According to the question,
l = 6w
and
Perimeter of the lawn = 630
2 [l + w] = 630
2 [6w + w] = 630
14w = 630
w = 45
Now,
l = 45[6] = 270
Thus, the required length and width of the lawn is given as Length = 270 feet and Width = 45 feet.
learn more about perimeter here:
brainly.com/question/6465134
#SPJ2
PLS PLSPKS PLS HELP URGENT ❗️❗️❗️❗️
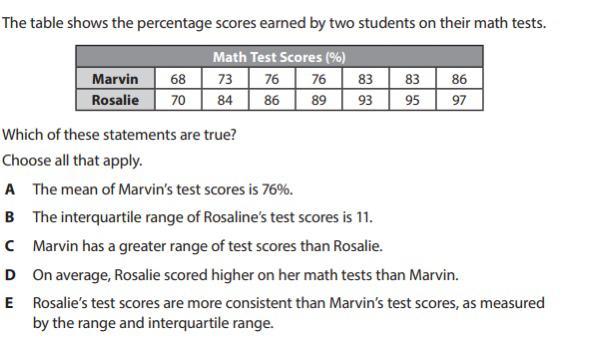
Answers
The true statement is that D. On average, Rosalie scored higher on her maths test that Marvin.
How to calculate the valueMean = (68+73+76+76+83+83+86)/7 = 77.14%
Therefore, this claim is untrue.
Rosaline's test results fall within a range of scores that is 11.
Q3 - Q1 = 16% is the interquartile range (IQR).
Therefore, this claim is untrue.
C) Marvin and Rosalie both had a wider range of test results.
The gap between the greatest and lowest scores is known as the range.
Range = 86 - 68 = 18% for Marvin.
Range = 97 - 70 = 27% for Rosalie
Therefore, this claim is untrue.
Rosalie performed better than Marvin on math exams on average.
Rosalie's test results' average were calculated as follows: Mean = (70+84+86+89+93+95+97)/7 = 87.14%
So, this assertion is accurate.
Learn more about range on
https://brainly.com/question/26098895
#SPJ1
Which of the following is NOT a true statement?
pls answer i'll give brainliest

Answers
Answer:
C.) AFD measures 30°
Step-by-step explanation:
it is 150 degrees
Answer:
the answer is C
Step-by-step explanation:
A) angle EFC is 80 degrees so a is a true statement
B) angle BFC is 60 degrees and angle DFE is 30 degrees 60+30=90 so that's a true statement
D) angle AFB is 40 degrees and angle CFD is 50 degrees 40+50=90 so that a true statement
that leaves C and angle AFD is more than 30 degrees its 150 degrees
Manipulate the radius of the sphere, setting it to different values. In the table below, record each radius you chose and the exact volume of the sphere (in terms of π). Also calculate the decimal value of each volume, and verify that it matches the volume displayed by the tool. (You might see some discrepancies in the tool due to rounding of decimals.)
Answers
Answer:
641654654
Step-by-step explanation:
Answer:
1) r=9 v=972
2) r=6 v=288
3) r=12 v=2,304
Step-by-step explanation:
Sample Answer on edmentum
help me with maths pls

Answers
After answering the given query, we can state that the solutions to the simultaneous equations are (x, y) ≈ (3.1, 10.2) and (x, y) ≈ (-1.9, 0.2).
What is a linear equation?In mathematics, a linear equation has become one that takes the form y=mx+b. The inclination is B, and the y-intercept is m. Since y and x are variables, the preceding clause is frequently referred by the term a "linear equation involving two variables."
Bivariate linear equations are linear equations with two variables. Linear equations can be found in many places, including 2x - 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, and 3x - y + z = 3. When the formula has the structure y=mx+b, where m denotes the slope and b the y-intercept, it is often referred to because of being quadratic.A mathematical equation is said to be linear if its solution has the form y=mx+b, where m stands for the slope and b for the y-intercept.
To show that 3y² - 10y - 24y¯47 = O, we need to find constants C and k such that |3y² - 10y - 24y¯47| ≤ C|y| for all y > k.
3y² - 10y - 24y¯47 ≤ 3y² + 10|y| + 24
3y² + 10|y| + 24 ≥ 3y² - 10y - 24y¯47 for y ≥ 5
C = 6:
|3y² - 10y - 24y¯47| ≤ 6|y| for y ≥ 5
3y² - 10y - 24y¯47 = O.
b) Using the result from part a), we can rewrite the simultaneous equations as:
3y² - 10y - 24y¯47 = O
y - 2x = 4
y = 2x + 4
3(2x + 4)² - 10(2x + 4) - 24y¯47 = O
12x² - 8x - 79 = O
x = (8 ± √(8² + 41279))/24
x ≈ 3.1 or x ≈ -1.9
y ≈ 10.2 or y ≈ 0.2
Therefore, the solutions to the simultaneous equations are (x, y) ≈ (3.1, 10.2) and (x, y) ≈ (-1.9, 0.2).
To know more about linear equation visit:
brainly.com/question/11897796
#SPJ1
The table shows values for two differentiable functions, a and c. Use the values from the table to answer the questions that follow. I 5 6 7 8 9 10 a(x) a'(x) c(x) c'(x) 10 7 6 5 9 9 5 6 5 6 7 7 7 5 10 8 6 10 8 9 8 8 9 10 Find r' (9) if r(x) = c(x) a(x). Answer: r' (9) • Find v'(8) if v(x) = Answer: v'(8) = c(x) Find h' (5) if h(x) = c(a(x)). Answer: h' (5) = • Find b' (10) if b(x) = c(c(x)). Answer: b'(10) =
Answers
The answers for the given differentiable functions are:
- r'(9) = 102
- v'(8) = 5
- h'(5) = 42
- b'(10) = 48.
To answer the questions, we need to differentiate the given functions based on the values provided in the table. Let's go through each question one by one:
1. Find r'(9) if r(x) = c(x) * a(x):
To find r'(9), we need to differentiate the function r(x) = c(x) * a(x) and evaluate it at x = 9.
From the table, we can see that c(9) = 9 and a(9) = 8.
Differentiating c(x) and a(x), we find:
c'(x) = 6 and a'(x) = 6.
Now, we can differentiate r(x) using the product rule:
r'(x) = c'(x) * a(x) + c(x) * a'(x).
Plugging in the values:
r'(9) = c'(9) * a(9) + c(9) * a'(9)
= 6 * 8 + 9 * 6
= 48 + 54
= 102.
Therefore, r'(9) = 102.
2. Find v'(8) if v(x) = c(x):
To find v'(8), we need to differentiate the function v(x) = c(x) and evaluate it at x = 8.
From the table, we can see that c(8) = 7.
Differentiating c(x), we find:
c'(x) = 5.
Now, we can directly evaluate v'(8):
v'(8) = c'(8)
= 5.
Therefore, v'(8) = 5.
3. Find h'(5) if h(x) = c(a(x)):
To find h'(5), we need to differentiate the function h(x) = c(a(x)) and evaluate it at x = 5.
From the table, we can see that a(5) = 9 and c(9) = 8.
Differentiating a(x) and c(x), we find:
a'(x) = 7 and c'(x) = 6.
Now, we can differentiate h(x) using the chain rule:
h'(x) = c'(a(x)) * a'(x).
Plugging in the values:
h'(5) = c'(a(5)) * a'(5)
= c'(9) * 7
= 6 * 7
= 42.
Therefore, h'(5) = 42.
4. Find b'(10) if b(x) = c(c(x)):
To find b'(10), we need to differentiate the function b(x) = c(c(x)) and evaluate it at x = 10.
From the table, we can see that c(10) = 9.
Differentiating c(x), we find:
c'(x) = 8.
Now, we can differentiate b(x) using the chain rule:
b'(x) = c'(c(x)) * c'(x).
Plugging in the values:
b'(10) = c'(c(10)) * c'(10)
= c'(9) * 8
= 6 * 8
= 48.
Therefore, b'(10) = 48.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
-4x+3=9
x=
solve the equation
Answers
Answer:
x = 3/2 ( Answer in fraction )
x = 1.5 ( Answer in decimal )
the ramirez drove 200 miles using 10 gallons of gas they drove 280 miles using 14 gallons of gas how many miles did they drive per gallon
Answers
Answer:
Step-by-step explanation:
At the same time of a day, a man who is 72 inches tall casts a 43.2- inch shadow and his son cast a 27-inch shadow. Use similar triangle to determine the height of the man son. state the postulate or theorem that can be used to provide the triangle are similar and then justify your answer. Help!

Answers
Answer: x = 40
Step-by-step explanation: 72/43.2 =x/27
1,944 =43.2 (round off)
x = 40
(i think!)
whats the distance between (-4, 6) and (3, -7)
Answers
Answer:
\( \boxed{ \bold{ \huge{ \boxed{ \sf{ \sqrt{218} \: \: units}}}}}\)
Step-by-step explanation:
Let the points be A and B
Let A ( -4 , 6 ) be ( x₁ , y₁ ) and B ( 3 , -7 ) be ( x₂ , y₂ )
Finding the distance between these two points
\( \boxed{ \sf{distance = \sqrt{ {(x2 - x1)}^{2} + {(y2 - y1)}^{2} } }}\)
\( \dashrightarrow{ \sf{ \sqrt{ {(3 - ( - 4))}^{2} + { (- 7 - 6)}^{2} } }}\)
\( \dashrightarrow{ \sf{ \sqrt{ {(3 + 4)}^{2} + {( - 7 - 6)}^{2} } }}\)
\( \dashrightarrow{ \sf{ \sqrt{ {7}^{2} + {13}^{2} } }}\)
\( \dashrightarrow{ \sf{ \sqrt{49 + 169} }}\)
\( \dashrightarrow{ \sf{ \sqrt{218}}} \) units
Hope I helped!
Best regards! :D
Can someone help me with this math homework please!

Answers
Answer:
A) Over the interval [-2.5, 0.5], the local maximum is 2--------------------------
Hope it helps...
Answer:
(A) Over the interval [-2.5, 0.5], the local maximum is 2.
Step-by-step explanation:
"Over the interval [-2.5, 0.5], the local maximum is 2."
Correct. The local maximum is the maximum, or highest point, of the graph in a certain area of interval. In [-2.5, 0.5], the highest point is at the y-value of 2.
"As the x-values go to positive infinity, the function's values go to negative infinity."
Wrong. As the x values go to positive infinity (meaning they go to the right, or positive side of the graph), the function goes up, meaning the function's values go to positive infinity.
"The function is decreasing over the interval (-1, 0.75)."
Wrong. Only from [-1, 0] is where that area of the graph decreases. The other half of it, (0, 0.75), is where the graph increases.
"The function is negative for the interval [-2, 0]."
Wrong. Only from [-1, 0] is the function negative. In the interval [-2, -1], the function is positive.
Hope that helps (●'◡'●)
Round to the nearest hundredth : 8.113
plz help :)
Answers
Answer:
\(8.11\)
Step-by-step explanation:
Rounded to nearest hundredth.
After Round to the nearest hundredth value of number is,
⇒ 8.11
We have to given that;
A number is,
⇒ 8.113
And, We an Round to the nearest hundredth.
Since, Rounding numbers refers to changing a number's digits such that it approximates a value.
Here, In number 8.113,
Digit in thousandth place is 3 which is less thn 5.
Hence, After Round to the nearest hundredth value of number is,
⇒ 8.11
Learn more about the rounding number visit:
brainly.com/question/27207159
#SPJ6
The missing quantity in the double number line

Answers
Answer: 1840 pounds
Step-by-step explanation:4x4=16
460 x 4 = 1840
Find solution of the Cauchy problem: 2xyux + (x² + y²) uy = 0 with u = exp(x/x-y) on x + y =
Answers
The solution of the Cauchy problem for the given partial differential equation 2xyux + (x² + y²) uy = 0 with the initial condition u = exp(x/(x-y)) on the curve x + y = C, where C is a constant, can be found by solving the equation using the method of characteristics.
To solve the given partial differential equation, we use the method of characteristics. Let's define a parameter s along the characteristic curves. We have the following system of ordinary differential equations:
dx/ds = 2xy,
dy/ds = x² + y²,
du/ds = 0.
From the first equation, we can solve for x: x = x0exp(s²), where x0 is a constant determined by the initial condition. From the second equation, we can solve for y: y = y0exp(s²) + 1/(2s), where y0 is a constant determined by the initial condition.
Differentiating x with respect to s and substituting it into the third equation, we obtain du/ds = 0, which implies that u is constant along the characteristic curves. Therefore, the initial condition u = exp(x/(x-y)) determines the value of u on the characteristic curves.
Now, we can express the solution in terms of x, y, and the constant C as follows:
u = exp(x/(x-y)) = exp((x0exp(s²))/(x0exp(s²) - y0exp(s²) - 1/(2s))) = exp((x0)/(x0 - y0 - 1/(2s))),
where x0 and y0 are determined by the initial condition and s is related to the characteristic curves. The curve x + y = C represents a family of characteristic curves, so C represents a constant.
In conclusion, the solution of the Cauchy problem for the given partial differential equation is u = exp((x0)/(x0 - y0 - 1/(2s))), where x0 and y0 are determined by the initial condition, and the curve x + y = C represents the family of characteristic curves.
To learn more about Cauchy problem click here: brainly.com/question/31988761
#SPJ11
2. Anita and Basia are selling packs of candy for a school fundraiser. Anita has six more
a
packs than Basia. If Basia has eight packs, write an expression using an operation to
represent how many packs of candy Anita has.
I need help
Answers
Answer:
a = b + 6
b = 8
Step-by-step explanation:
a = b + 6
b = 8
sinx= -29.3
solve the equation
Answers
Answer:
There is actually no solution.
The range of sines are -1 ≤ y ≤ 1. And -29.3 does not fall into the range, making this solution not logically possible to come to.
Determine the [OH] in a solution with a pH of 4.798. Your answer should contain 3 significant figures as this corresponds to 3 decimal places in a pH. [OH]= 62810 -^9 M
Answers
the [OH⁻] in the solution is approximately 6.281 × \(10^{(-10)}\) M.
To determine the [OH⁻] in a solution with a pH of 4.798, we can use the relationship between pH, [H⁺], and [OH⁻].
pH + pOH = 14
Since we have the pH value, we can calculate the pOH as follows:
pOH = 14 - pH
pOH = 14 - 4.798
pOH = 9.202
Now, we can convert pOH to [OH⁻]:
[OH⁻] = 10^(-pOH)
[OH⁻] = 10^(-9.202)
Using a calculator, we find:
[OH⁻] ≈ 6.281 × 10^(-10) M
To know more about pH visit:
brainly.com/question/2288405
#SPJ11
A package of 4 red,white and blue hats costs $8. What is the unit rate
Answers
Answer:
$2/ hat
Step-by-step explanation:
Find the unit rate:
$ to hats
8 to 4
Divide by four to get the unit rate; over 1
2 to 1
So, $2 per hat
Hope this helps!
Jina earns 9 dollars each hour working part-time at a bookstore. She earns one additional dollar for each book that she sells.
Let A be the amount (in dollars) that Karen earns in an hour if she sells B books.
Write an equation relating A to B. Then graph your equation using the axes below.
Answers
The equation relating A to B is A = 9 + B, and the graph is a line with a slope of 1 passing through the point (0, 9).
What is the equation and graph of A = 9 + B, where A represents Karen's earnings in dollars and B represents the number of books she sells?To write an equation relating A to B, we need to consider that Karen earns 9 dollars per hour working part-time at the bookstore.
Additionally, she earns one additional dollar for each book she sells.
Therefore, the equation relating A (the amount Karen earns in dollars) to B (the number of books she sells) can be expressed as:
A = 9 + BThis equation states that Karen's earnings in dollars (A) are equal to the base hourly wage of 9 dollars plus the additional earnings she receives for each book sold (B).
To graph this equation, we can plot the values on a coordinate plane. We'll assume B represents the horizontal axis (x-axis), and A represents the vertical axis (y-axis).
Here's the graph of the equation A = 9 + BOn the graph, the line starts at the point (0, 9) and has a slope of 1, indicating that for each additional book Karen sells, her earnings increase by 1 dollar.
Learn more about equation relating
brainly.com/question/14695415
#SPJ11
If I have a book that is 298 pages, and I read 20 pages a day, how long will it take me to read the entire book?
Also what is the formula to solve this problem problem!!
Answers
Answer:
Step-by-step explanation:
Given:
N₀ = 298 pages
N = 20 pages
You can apply the formula:
Number of days
D = [N₀ / N] + 1 = [298 / 20 ] + 1 =
= [14.9] + 1 = 14 + 1 = 15 day,
where the square brackets are the integer part of the number
If a book has 298 pages, and I read 20 pages a day, then it will take 15 days to read the entire book.
Total pages in the book= 298
Total pages that I daily read= 20
Then it will take 15 days to read the entire book.
The formula for this problem:
The solution to this type of problem can be figured out with the help of unitary method.
20 pages of a book can be read in = 1 day
1 page of a book can be read in = 1/20 days
298 pages of a book can be read in = 1/20×298 days = 14.9 days
But days cannot be 14.9, so it will be 15 days which is the nearest value of 14.9.
15 days it will take to read the entire book.
To know more about Unitary method:
https://brainly.com/question/22056199
Use the perpendicular slope 1/2 and the point
(-3,2) to find the equation of the line
y = -2x + 12
y = 1/2x + 1
y = 1/2x + 5
y = 1/2x +3.5
Answers
Answer:
4th option
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
given m = \(\frac{1}{2}\) , then
y = \(\frac{1}{2}\) x + c ← is the partial equation
to find c substitute (- 3, 2 ) into the partial equation
2 = - \(\frac{3}{2}\) + c ⇒ 2 + \(\frac{3}{2}\) = \(\frac{7}{2}\) = 3.5
y = \(\frac{1}{2}\) x + 3.5 ← equation of line
10+10+10+9 WILL MARK BRAINLIEST ANSWER PLS NEED HELP ASAP
Answers
Answer:
39 SIR
Step-by-step explanation:
Help help help help help

Answers
for example with 4-6a
you would put 4 = 2•2 so 2 is it’s GCF
and 6= 3•2 so 3 is it’s GCF
however the question is asking for the combined GCF (meaning the whole problem)
so 4-6a’s GCF would be 2 considering it is the only greatest common factor between BOTH numbers
for 12a^2 - 8a you would use the same method:
12a^2= 3a•2a•2 and 3a is it’s GCF
8a = 2•2•2a and 2a is it’s GCF
but combined, the greatest factor BOTH numbers have in common is 2a, so 2a is the answer!
i hope i helped you :)!❤️
if a circumference is 12 pi ft what is the area
Answers
Work Shown:
Use the circumference to determine the radius.
C = 2pi*r
12pi = 2pi*r
12 = 2r
r = 12/2
r = 6
Then find the area.
A = pi*r^2
A = pi*6^2
A = 36pi
The units for the area will be "square feet" which can be abbreviated to "sq ft", ft^2 or \(\text{ft}^2\)
Find the probability that a randomly selected point within the circle falls in the red shaded area

Answers
The probability that a randomly selected point within the circle falls in the red shaded area is 15.9%
How to determine the probability?The radius is given s:
r = 4 cm
So, the area of the triangle is
A1 = 0.5r^2
Similarly, the area of the circle is
A2 = πr^2
The probability that a randomly selected point within the circle falls in the red shaded area is
P = A1/A2
This gives
P = 0.5r^2/πr^2
Evaluate
P = 15.9%
Hence, the probability that a randomly selected point within the circle falls in the red shaded area is 15.9%
Read more about probability at:
https://brainly.com/question/24756209
#SPJ1
A rectangle is 8 feet longer than it is wide. find the dimensions of the rectangle if its area is 345 sq-feet.
Answers
The width of rectangle is 15 feet and the length of rectangle is 23 feet.
According to the statement
Width of rectangle = x
Length of rectangle = x+10
Area of rectangle = 345 sq-feet.
we know that the area of rectangle is
Area of rectangle = L*W
Substitute the values in it then
345 = (x) (x+8)
345= (x)^2 + 8x
(x)^2 + 8x - 345 = 0
By factorisation
(x-15) (x+23) = 0
So, width of rectangle is 15 feet and the length of rectangle is 23 feet.
Learn more about AREA here https://brainly.com/question/19819849
#SPJ4