Answers
Answer:
First answer
Step-by-step explanation:
It makes sense to me... I think I am right... I know think is not definate But I have good grades.. So... (BTW I am socially if I sound off or odd that is just me)
Related Questions
(-31/2)-(-41/4)=-7/2-(17/4)=
Answers
compute the accumulated value of $8600at 6.45% after 8
months (simple interest)
Answers
The accumulated value of $8600 at 6.45% after 8 months (simple interest) is $8971.90.
To compute the accumulated value of $8600at 6.45% after 8 months (simple interest), we need to use the formula for simple interest, which is given by:
I = P × r × t
Where, I is the interest earned, P is the principal amount, r is the interest rate, and t is the time in years.
Here, we have t in months, so we need to convert it into years by dividing by 12.
So, t = 8/12 = 2/3 years.
Now, substituting the given values, we get:
I = 8600 × 6.45/100 × 2/3 = $371.90
Therefore, the accumulated value of $8600 at 6.45% after 8 months (simple interest) is $8600 + $371.90 = $8971.90.
Learn more about interest rate at:
https://brainly.com/question/23920675
#SPJ11
Question 2 Multiple Choice Worth 5 points)
(03.01 LC)
The leg of a right triangle is 2 units and the hypotenuse is 4 units. What is the length, in units, of the other leg of the triangle?
O2 units
0 6 units
O V12 units
O V20 units

Answers
Answer:
√20 units.
Step-by-step explanation:
Please see attached photo for diagram.
The other leg of the triangle is x as shown in the attached photo.
Using the pythagoras theory, we can obtain the the value of x as follow:
x² = 4² + 2²
x² = 16 + 4
x² = 20
Take the square root of both side.
x = √20 units
Therefore, the value of the other leg x of the triangle is √20 units

Answer:
\(\sqrt{} 20\) is your answer hope this helps
Step-by-step explanation:
Please help I need the answer immediately

Answers
Answer:
\(-\frac{11}{12}\)
Step-by-step explanation:
Step 1- Add.
\(\frac{\frac{5}{8} +\frac{3}{4} }{\frac{-2}{3}-\frac{5}{6} }\) = \(\frac{\frac{11}{8} }{\frac{-3}{2} }\)
Step 2- Divide and rewrite.
\(-\frac{\frac{11}{8} }{\frac{3}{2} }\) = \(-\frac{11}{12}\)
Evaluate
35.63% of 446.51cm
Give your answer rounded to 2 Dp
Answers
Answer:
159.09
Step-by-step explanation:
.3563 * 446.51 = 159.09
Select all the correct statements about the fractional equation (x/x-1) - (3/x) = 1/x-1
Only x=3 is a solution
Both x=3 and x=1 are solutions
Only x=1 is and extraneous root
Only x=3 is an extraneous root
Answers
Answer: only x=3 is a solution and only x=1 is an extraneous root
For the given expression (x/x-1) - (3/x) = 1/x-1 both x=3 and x=1 are solutions. The correct option is B.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the expression is (x/x-1) - (3/x) = 1/x-1. Check the solution of the expression,
(x/x-1) - (3/x) = 1/x-1
( 3 / 3 - 1 ) - ( 3 / 3 ) = 1 ( 3 - 1 )
( 3 / 2 - 1 ) = 1 / 2
1 / 2 = 1/2
For x = 1 the value is the same.
Therefore, both 3 and 1 are solutions to the given formula (x/x-1) - (3/x) = 1/x-1.
To know more about an expression follow
https://brainly.com/question/6241556
#SPJ2
Hello, I don’t understand this equation and the steps to do it so could you help me out?
Circumference= C=(pie)d
Solve for d in the equation.
Answers
Answer:
c is circumference which is equal to 3.14 multiplied by d
Step-by-step explanation:
write a positive or negative integer that represents the situation. the temperature is 31 degrees above zero.
Answers
The integer that represents the given situation is a positive 31.
The temperature being 31 degrees above zero means that it is warmer than the freezing point of water. In this context, "above zero" refers to the Celsius or Fahrenheit scale, where zero represents the freezing point of water. Therefore, a temperature of 31 degrees above zero is a positive value indicating a warm temperature.
In this case, it can be assumed that the temperature is being measured in Celsius since 31 degrees above zero on the Fahrenheit scale would correspond to a very high temperature of approximately 87 degrees Fahrenheit. Overall, the integer that represents this situation is positive 31, which signifies a warm temperature above the freezing point.
Learn more about Positive:
brainly.com/question/23709550
#SPJ11
your friend deposits $5000 in an investment account that earns 6.3% annual interest. find the balance after 6 years when the interest is compounded monthly
Answers
The balance after 6 years when the interest is compounded monthly is $7289.60
How to find the balance after 6 years when the interest is compoundedTo find the balance after 6 years when the interest is compounded monthly, we can use the formula:
A = P(1 + r/n)^(nt)
where:
A = the final balanceP = the principal amount (the initial deposit)r = the annual interest rate (as a decimal)n = the number of times the interest is compounded per yeart = the time in yearsIn this case, P = $5000, r = 6.3% = 0.063 (annual interest rate as a decimal), n = 12 (since interest is compounded monthly), and t = 6.
Plugging in these values, we get:
A = $5000(1 + 0.063/12)^(12*6)
Evaluate
A = $7289.60
Therefore, the balance after 6 years when the interest is compounded monthly is $7289.60
Read more about compound interest at
https://brainly.com/question/28020457
#SPJ1
A large sphere at an amusement park is 165 feet in diameter. Which of the following is closest to the volume, in cubic feet, of the sphere?
261,000
261,000
2,351,000
2,351,000
18,810,000
18,810,000
41,210,000
Answers
Answer:
2,351,000
Step-by-step explanation:
closest to the volume in cubic feet
Which statement can you use to conclude that quadrilateral xyzw is a parallelogram

Answers
Answer: Option (4)
Step-by-step explanation:
A quadrilateral with two pairs of opposite congruent sides must be a parallelogram.
what is 28.5 inches in height?
Answers
The Fun Committee is hosting the Annual City Festival. Jennifer is in charge of the committee and is planning a race to raise money for the Festival. The runners will earn money from donors for the number of miles they run. If the runners start at the park, run to City hall, and then run back to the park, how many total miles will each runner run? Show your work and leave your answer in simplest radical form if necessary.
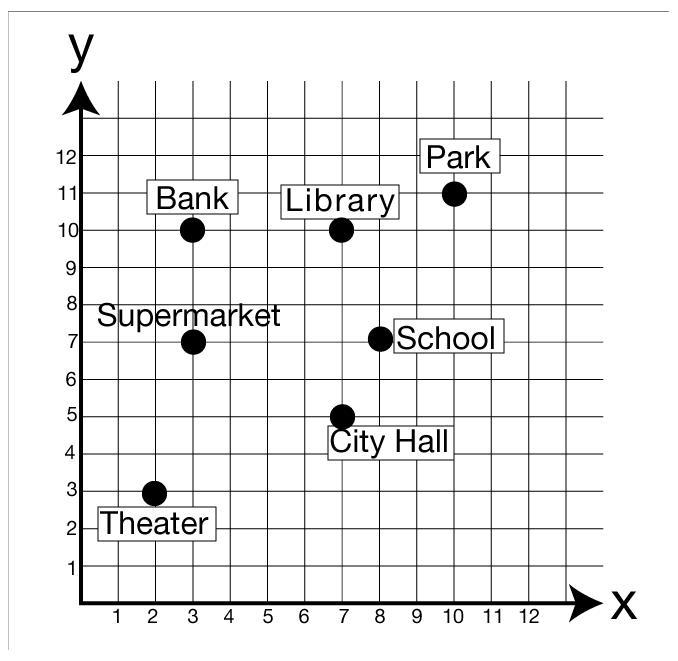
Answers
Answer: \(6\sqrt{5}\) miles
This is the same as writing 6*sqrt(5) miles
==========================================================
Work Shown:
P = park
C = city hall
Point P is at the location (10,11)
Point C is at the location (7,5)
Apply the distance formula to find the length of segment PC
\(d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\d = \sqrt{(10-7)^2 + (11-5)^2}\\\\d = \sqrt{(3)^2 + (6)^2}\\\\d = \sqrt{9 + 36}\\\\d = \sqrt{45}\\\\d = \sqrt{9*5}\\\\d = \sqrt{9}*\sqrt{5}\\\\d = 3\sqrt{5}\\\\d \approx 6.7082039\\\\\)
The exact distance between the park (P) and city hall (C) is \(3\sqrt{5}\) miles.
This doubles to \(2*3\sqrt{5} = 6\sqrt{5}\) miles because the runners go from P to C, then back to P again. In other words, they run along segment PC twice. This is assuming there is a straight line road connecting the two locations.
Extra info:
\(6\sqrt{5} \approx 13.41641\) so the runner travels a total distance of roughly 13.4 miles.
Consider the expression 8ab +3b + 16 - 4a ·How many terms are there ? ·How many factors are in the term (identify them ) · Which term is a constant ?
Answers
Answer:
the answers are below
Step-by-step explanation:
1: 4
2: 3 and they are 8ab, 3b, and 4a
3: 16
Answer:
8 a b - 4 a + 3 b + 16. Simplify: 8 a b - 4 a + 3 b + 16 Answer: 8 a b - 4 a + 3 b + 16
Step-by-step explanation: Coefficient is any of the factors with the sign of the term. ... The given algebraic expression has three terms, namely, 4a 4b2c – 3a3b2c and 3/2 ab3c2
Find the constant of direct variation when x = 3 and y = -12
Answers
Answer:
constant = b = -15
Step-by-step explanation:
3 + b = -12
b = -12 - 3
b = -15
What is the value of x in the triangle? a 45-45-90 triangle with leg length 7 and hypotenuse length x a. B. C. D.
Answers
The value of x in the given 45-45-90 triangle is 9.89.
The given triangle is a right-angled triangle which can be solved using the Pythagoras theorem. The Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the square of the base and the square of the perpendicular. This theorem can be applied to all right-angled triangles.
In the given triangle, we have been told that the length of both legs is 7. Now, after applying the theorem -
= 7²+7² = H²
= 49 + 49 = H²
= 98 = H²
= √98 = H
= 9.89 = H
Hence, this is the value of x.
Learn more about the Pythagoras Theorem on
https://brainly.com/question/21926466?referrer=searchResults
#SPJ4
Please help with math

Answers
Answer:
sin x= opp/hyp
sin x=18/30
sin x =3/5
cos x= adj/hyp
cos x=24/30
cos x=4/5
tan x=opp/adj
tan x=18/24
tan x=3/4
Using the rule that cos3θ = 4(cosθ)^3 − 3 cosθ, show that cos 2π/9 is a root of the equation 8x^3 − 6x + 1 = 0

Answers
Answer:
Below in bold.
Step-by-step explanation:
Let x = cosθ, then
8(cosθ)^3 − 6cosθ + 1 = 0
---> 2(4(cosθ)^3 − 3 cosθ) + 1 = 0
---> 2(cos3θ) + 1 = 0
---> cos3θ = -1/2
---> θ = 2π/9
Therefore cos θ = = cos(2π/9) = x, and
cos(2π/9) is a root of the given eqation.
Can someone please help me with this?( there is a part 2)


Answers
Part A:
Since Juanita had at first $25
Since she earns $11 per hour
Then her total earning in x hours is
\(11x+25\)Since she needs at least $58 to buy new shoes
At least means greater than or equal, then the inequality should be
\(11x+25\ge58\)Part B:
Let us solve it by subtracting 25 from each side
\(\begin{gathered} 11x+25-25\ge58-25 \\ 11x\ge33 \end{gathered}\)Divide each side by 11
\(\begin{gathered} \frac{11x}{11}\ge\frac{33}{11} \\ x\ge3 \end{gathered}\)Then the answer is the 3rd choice
Solve for x - (4x-5y) = (-5y+4)
Answers
Answer:
X= 10/3y + -4/3
Step-by-step explanation:
Step One: add -5y to both sides
Step two: divide both sides by -3
Answer:
-x=1 1/3
Step-by-step explanation:
x-(4x-5y)=(5y+4)
x-4x+5y=5y+4
-3x+5y=5y+4
5y-5y=0
-3x=4
x=4÷3
4÷3=1 1/3
Why
is the use and interpretation of an R or s chart so critical when
examining an X-bar chart?
Answers
The use and interpretation of an R or s chart are critical when examining an X-bar chart because they provide additional information about the variation within the subgroups. This allows for a more comprehensive analysis of the process and helps identify any issues or sources of variability.
When using an X-bar chart, the focus is on monitoring the process mean or average. However, the X-bar chart alone does not provide information about the variation within the subgroups. This is where the R or s chart comes into play. The R chart measures the range of values within each subgroup, while the s chart measures the standard deviation.
By using an R or s chart alongside the X-bar chart, we can assess the variability within the subgroups and determine if it is stable over time. If the variation within the subgroups is high and unpredictable, it may indicate that the process is out of control or that there are sources of variation that need to be addressed. The R or s chart provides additional insights into the process performance and helps in identifying the presence of special causes of variation.
In summary, the use and interpretation of an R or s chart in conjunction with an X-bar chart allow for a more comprehensive analysis of process variation. This helps in understanding the stability and capability of the process and enables appropriate actions to be taken to improve quality and performance.
learn more about X-bar chart here
https://brainly.com/question/31861365
#SPJ11
Which statement is NOT true about a regular 16-gon?

Answers
Therefore , the solution of the given problem of angles comes out to be following about a normal 16-gon is FALSE:
What does an angle mean?The top but also bottom of wall separate the two circular edges that make the sides of a skew in Euclidean space. A junction point may develop when two beams collide. Another result of two things interacting is an angle. They most closely resemble dihedral shapes. Two line beams can be arranged in different ways at their extremities to form a two-dimensional curve.
Here,
The following about a normal 16-gon is FALSE:
c. The internal angle measure's total value is 28800.
We can use the following method to determine the total interior angle measure of a regular 16-gon:
Sum of internal angles equals (n - 2)180°, where n is the number of sides.
=> With n = 16, we obtain:
=> Interior angle total = (16 - 2) 180 = 2520 degrees.
Because of this, it is accurate to say that
=> 2520 degrees, not 28800, make up the interior angle measure of a regular 16-gon.
To know more about angles visit:
https://brainly.com/question/14569348
#SPJ1
The drama club is running a lemonade stand to raise money for its new production. A local grocery store
donated cans of lemonade and bottles of water. Cans of lemonade sell for $2.50 each and bottles of water
sell for $1.25 each. The club needs to raise at least $600 to cover the cost of renting costumes. The students
can accept a maximum of 460 cans and bottles.
Write a system of inequalities that can be used to represent this situation.
The club sells 144 cans of lemonade. What is the least number of bottles of water that must be sold to cover
the cost of renting costumes? Justify your answer.
Answers
Answer:
Part A
x + y ≤ 460...(1)
2.5·x + 1.25·y ≥ 600...(2)
Part B
The number of bottles of water the student must sell ≥ 192 bottles of water
Step-by-step explanation:
The given parameters are;
The selling price of each can of lemonade = $2.50
The selling price of each bottle of water = $1.25
The amount of money the club needs to raise = $600
The maximum number of cans and bottles the students can accept = 460
Part A
Let 'x' represent the number of cans of lemonade the students accept, and let 'y' represent the number of bottles the student accept, the system of inequalities that can be used to represent the situation can be presented as follows;
x + y ≤ 460...(1)
2.5·x + 1.25·y ≥ 600...(2)
Part B
The number of cans of lemonade the club sells, x = 144
The number of bottles of water the student must sell to cover the cost of costumes, 'y', is given from the second inequality as follows;
2.5 × 144 + 1.25·y ≥ 600
1.25·y ≥ 600 - 2.5 × 144 = 240
1.25·y ≥ 240
y ≥ 240/1.25 = 192
y ≥ 192
The number of bottles of water the student must sell = 192 bottles of water
What is an equivalent ratio to 3/4?
Answers
Answer:
6/8
Step-by-step explanation:
multiply both of them by 2 and its equal.
you get 6/8
In each of Problems 1 through 6:
a. Show that the given differential equation has a regular singular point at x0.
b. Determine the indicial equation, the recurrence relation, and the roots of the indicial equation.
c. Find the series solution (x >0) corresponding to the larger root.
d. If the roots are unequal and do not differ by an integer, find the series solution corresponding to the smaller root also.
1. 2x"+y'+xy =0
2. x^2y"+xy'(x^2-1/9)y=0
3. xy"+y=0
4. xy"+y''-y=0
5. x^2y"+xy'+(x-2)y=0
6. xy"+(1-x)y'-y=0
Answers
The tasks offered to require you to determine the series solution to a differential equation. For each issue, we must establish if the differential equation has a regular singular point for a given value of x, as well as the indicial equation, recurrence relation, and indicial equation roots. Consequently, if the bigger and smaller roots exist, we can obtain the series solution to the differential equation.
1. a) Regular singular point at x0=0
b) Indicial equation: r(r-1)+r=0, which simplifies to r^2=0. The roots are r1=r2=0.
c) y(x) = c0 + c1*x, where c0 and c1 are constants of integration.
d) N/A as the roots are equal.
2. a) Regular singular point at x0=0
b) Indicial equation: r(r-1)+r/9=0, which simplifies to r(r-1+1/9)=0. The roots are r1=0 and r2=1-1/3=2/3.
Recurrence relation: an=-(2n-1)/n(3n+1)an-1
c) y(x) = c0 + c1x^(2/3) - 1/21x^(8/3) + 2/495x^(14/3) - 26/25515x^(20/3) + ...
d) y(x) = c2x^0 + c3x^(-1/3) - 5/63x^(5/3) + 11/2079x^(11/3) - 301/54235*x^(17/3) + ...
3. a) Regular singular point at x0=0
b) Indicial equation: r(r-1)=0. The roots are r1=0 and r2=1.
Recurrence relation: an=-(1/2)an-1
c) y(x) = c0 + c1*x
d) y(x) = c2 + c3/x
4. a) Regular singular point at x0=0
b) Indicial equation: r(r-1)-1=0, which simplifies to r^2-r-1=0. The roots are r1=(1+sqrt(5))/2 and r2=(1-sqrt(5))/2.
Recurrence relation: an=-[2(n-1)+1-1]/(n(n+1)-1)(r1(n-1)+r2n)an-1
c) y(x) = c0 + c1exp(r1x) + c2exp(r2x)
d) y(x) = c3exp(r2x)
5. a) Regular singular point at x0=0
b) Indicial equation: r(r-1)+r+2=0, which simplifies to r^2=1. The roots are r1=1 and r2=-1.
Recurrence relation: for r1: an=-1/[(n+2)(n+1)]an-1, for r2: an=1/(n(n-1)+2n-6)an-1
c) y(x) = c0 + c1x - x^2/3 + 4/45x^4 - 2/945*x^6 + ...
d) y(x) = c2 + c3/x^2
6. a) Regular singular point at x0=0
b) Indicial equation: r(r-1)+(1-x)r=0, which simplifies to r^2-xr=0. The roots are r1=0 and r2=x.
Recurrence relation: an=-an-1/(n(1-x+n))
c) y(x) = c
Learn more about differential equations:
https://brainly.com/question/25731911
#SPJ11
How to simplify radicals with variables and exponents?
Answers
Radicals expression with variables and exponents can be simplify by:
Separate the number and variablesTry to find variables with even exponentsTry to breakdown the number into any factors that are perfect squareTry to rewrite both number and variables into square exponent Separate the squared factors into individual radicalsTake the square root of each radicalSimplify and multiplyTo help us understand each step better, we will take an example of a radical expression with variables and exponents of: \(\sqrt{16a^{3}b^6c^5 }\)
First, we need to separate the number and variables:
\(\sqrt{16a^3b^6c^5}=\sqrt{16} \sqrt{a^3b^6c^5}\)
Next, we will try to find variables with even exponents:
\(\sqrt{16} \sqrt{a^3b^6c^5} = \sqrt{16} \sqrt{a.a^2.b^6.c^4.c^}\)
Remember that:
(xᵃ)ᵇ = xᵃᵇ; then:
\(\sqrt{16}\sqrt{a.a^2.b^6.c^4.c} =\sqrt{16}\sqrt{a.a^2.(b^3)^2.(c^2)^2.c}\)
We try to breakdown any number into any factor that are perfect square:
\(\sqrt{16}\sqrt{a.a^2(b^3)^2.(c^2)^2.c} = \sqrt{4 .4} \sqrt{a.a^2(b^3)^2.(c^2)^2.c}\)
We will rewrite both number and the variables into a square exponents:
\(\sqrt{4 .4} \sqrt{a.a^2(b^3)^2.(c^2)^2.c} = \sqrt{4^2} \sqrt{a.a^2(b^3)^2.(c^2)^2.c}\)
We will separate the squared factors into individual radicals:
\(\sqrt{4 ^2} \sqrt{a.a^2(b^3)^2.(c^2)^2.c} = \sqrt{4^2} \sqrt{a^2} .\sqrt{(b^3)^2} \sqrt{(c^2)^2} \sqrt{a.c}\)
We take the square root of each radical into:
\(\sqrt{4^2} \sqrt{a^2} .\sqrt{(b^3)^2} \sqrt{(c^2)^2} \sqrt{a.c} = 4|a|.|b^3|.c^2\sqrt{ac}\)
We just need to simplify our last equation into:
\(4|a|.|b^3|.c^2\sqrt{ac} = 4|ab^3|c^2\sqrt{ac}\)
Learn more about Radical Expression here: brainly.com/question/3796764
#SPJ4
1.
Find the perimeter of the figure below.
7 cm
2 cm
4 cm
2 cm
4 cm
4 cm

Answers
Answer:
42 cm
Step-by-step explanation:
7+4+2+4+2+4+7+12
Write an equation of the parabola that passes through the point (3, 8) and has vertex (9,5). Use the variables x and y.
An equation of the parabola is y =
Answers
An equation of the parabola that passes through the point (3, 8) and has vertex (9, 5) is y = 1/12(x - 9)² + 5.
How to write the vertex form of a parabola?In this exercise, you're required to write an equation of the parabola in vertex form by using the completing the square method. Mathematically, the vertex form of a parabola is represented by this mathematical expression:
y = a(x - h)² + k
Where:
h and k represents the vertex of the equation.
Next, we would determine the value of a as follows:
8 = a(3 - 9)² + (5)
8 = a(-6)² + 5
8 = 36a + 5
36a = 8 - 5
36a = 3
a = 3/36
a = 1/12
Substituting the given parameters into the equation, we have;
y = a(x - h)² + k
y = 1/12(x - 9)² + 5
Read more on parabola here: brainly.com/question/27814369
#SPJ1

the volume of a right circular cylinder is V=pi r^2h , where r is the radius h is the height. What is the volume of the right circular cylinder with a radius of x^3 and a height of x^2 in the terms of x and pi.
Answers
Work Shown:
V = pi*r^2*h
V = pi*(x^3)^2*x^2
V = pi*x^(3*2)*x^2
V = pi*x^6*x^2
V = pi*x^(6+2)
V = pi*x^8
Answer:
πx^8
Step-by-step explanation:
V=πr²h
Now plugin r=x³ and h=x² in the formula above:
V=π(x³)²(x²) multiply powers 3x2=6
=π(x^6)(x²) = πx^8 add powers 6+2=8
Please help ASAP ‼️‼️‼️‼️‼️‼️

Answers
Answer:
B. \(\bold{g(x)=(\frac12x)^2}\)Step-by-step explanation:
vertex of g(x) is (0, 0), so:
\(g(x)=a(x-0)^2+0\\\\g(x)=ax^2 \qquad and\qquad (2,\,1)\in g(x)\\\\1=a\cdot2^2\\1=4a\\a=\frac14\\\\g(x)=\frac14x^2=(\frac12x)^2\)
