PLEASE HELPP
Linus wants to have 500 copies of his resume printed. His local print shop charges $18.50 for the first 200 copies and $9 for every 100 additional copies. How much will the 500 copies cost?
A)$46.25
B)$45.50
C)$45.00
D)$46.00
Answers
Related Questions
consider the equation 3.45 log (y) = 2.33 + 87.6 log(x). what is the elasticity?
Answers
To determine the elasticity, we need to differentiate both sides of the equation with respect to x and then multiply by (x/y):
Differentiating the equation with respect to x:
3.45 * d/dx(log(y)) = 87.6 * d/dx(log(x))
Using the property of logarithmic differentiation, we have:
3.45 * (1/y) * dy/dx = 87.6 * (1/x) * dx/dx
Simplifying and rearranging the equation:
(1/y) * dy/dx = (87.6/3.45) * (1/x)
(1/y) * dy/dx = 25.43/x
Multiplying both sides by (x/y):
dy/dx = (25.43/x) * (x/y)
dy/dx = 25.43/y
The elasticity is given by the ratio of the derivative of y with respect to x to the ratio of y to x. In this case, the elasticity is:
Elasticity = dy/dx * (x/y)
Substituting the value we obtained for dy/dx:
Elasticity = (25.43/y) * (x/y)
Elasticity = 25.43 * (x/y^2)
Therefore, the elasticity is given by 25.43 times the ratio of x to y squared.
Learn more about differentiate here:
https://brainly.com/question/24062595
#SPJ11
A poll of teenagers in one town showed that 43 % play a team sport. It also showed that 21% play varsity team sports. Find the probability that a teenager plays varsity sports, given that the teenager plays a team sport.
Answers
The probability that a teenager plays varsity sports, given that they play a team sport, is approximately 0.4884 or 48.84%.
To find the probability that a teenager plays varsity sports given that they play a team sport, we can use conditional probability.
Let's denote:
A: Playing varsity sports
B: Playing a team sport
We are given:
P(B) = 43% = 0.43 (Probability of playing a team sport)
P(A) = 21% = 0.21 (Probability of playing varsity sports)
We need to find PA(|B), which represents the probability of playing varsity sports given that the teenager plays a team sport.
The conditional probability formula is:
P(A|B) = P(A ∩ B) / P(B)
P(A ∩ B) represents the probability of both A and B occurring simultaneously.
In this case, the probability of a teenager playing varsity sports and a team sport simultaneously is not given directly. However, we can make an assumption that all teenagers who play varsity sports also play a team sport. Under this assumption, we can say that P(A ∩ B) = P(A) = 0.21.
Now we can calculate P(A|B):
P(A|B) = P(A ∩ B) / P(B)
= 0.21 / 0.43
≈ 0.4884
Therefore, the probability that a teenager plays varsity sports, given that they play a team sport, is approximately 0.4884 or 48.84%.
To learn more about probability click here:
brainly.com/question/22946813
#SPJ11
PLEASE HELP ME!!!! Thank you so muuuccccchhhh :)
Do you know how fast last year’s winner was traveling?
The catamaran in San Francisco
Answers
Answer:
43 knots
Step-by-step explanation:
43 bro
hope dat helps
A retailer agreed to take 5000 ball point pen however he found that 12 percent are faulty what is the percentage decreasment
Answers
The percentage decrease in the number of pens is 88%. This means that 88% of the initial quantity of pens are still usable, while 12% are faulty.
What is the percentage decrease if 12% of 5000 ballpoint pens are found to be faulty?To calculate the percentage decrease, we need to find the difference between the initial quantity and the faulty quantity, and then express it as a percentage of the initial quantity.
Initial quantity = 5000 pens
Faulty percentage = 12%
Number of faulty pens = 12% of 5000 = (12/100) ˣ 5000 = 600 pens
The decrease in quantity = Initial quantity - Faulty quantity = 5000 - 600 = 4400 pens
Percentage decrease = (Decrease in quantity / Initial quantity) ˣ 100
= (4400 / 5000) * 100 = 88%Learn more about percentage decrease
brainly.com/question/15221868
#SPJ11
Which transformation preserves the property of a shape of a figure
Answers
an online coupon service has offers for free samples. part: 0 / 20 of 2 parts complete part 1 of 2 (a) how many different requests are possible if a customer must request exactly free samples? the number of different requests is .
Answers
The number of possible requests for free samples is 5^1 = 5. This means that the customer has 5 different requests that they can make for free samples.
The number of possible requests for free samples can be calculated using the combination formula. The combination formula is used to calculate the number of combinations with repetitions of size “n” taken from a set of “r” elements . The formula is: \(C(n,r) = n^r\) In this case, n = number of requests (1 request) and r = number of free samples offered (let’s say, 5). Therefore, the number of possible requests for free samples is\(5^1 = 5.\)This means that the customer has 5 different requests that they can make for free samples.
Learn more about samples here:
https://brainly.com/question/15659544
#SPJ4
how did the results of the election of 1860 demonstrate the breakdown or division of the country and how is it possible.
Answers
The Civil War was fought between the North and the South, and it was the bloodiest conflict in American history. The Civil War ended in 1865 with the defeat of the South and the reunification of the country.
The election of 1860 saw the defeat of the nationalistic candidate Stephen A. Douglas, which demonstrated the division of the country, and this led to the breakdown of the Union in 1861. The election of 1860 demonstrated the deep political, social, and economic divisions that had existed in the country since the time of the founding fathers and how these divisions could lead to the collapse of the government itself.The election of 1860 saw the defeat of the nationalistic candidate Stephen A. Douglas, who was defeated by Abraham Lincoln, who was the candidate of the Republican Party. The election of 1860 was the first in which the Democratic Party had split into two, and as a result, the party was unable to present a united front. The election also saw the rise of the Republican Party, which was a party that was strongly opposed to the extension of slavery into the western territories. The Republican Party had been formed in 1854, in opposition to the Kansas-Nebraska Act, which had allowed the people in the western territories to decide for themselves whether or not to allow slavery. The Republican Party had quickly become the party of the North, and the party's platform was focused on protecting the interests of the North, and opposing the interests of the South.The election of 1860 demonstrated how the country was deeply divided, and how this division could lead to the breakdown of the government itself. The election was followed by a series of events that led to the secession of the southern states, and the subsequent Civil War. The Civil War was fought between the North and the South, and it was the bloodiest conflict in American history. The Civil War ended in 1865 with the defeat of the South and the reunification of the country.
Learn more about war :
https://brainly.com/question/11874600
#SPJ11
What is the perimeter of rhombus lmno? 20 units 24 units 40 units 48 units
Answers
The perimeter of the rhombus LMNO is 48 units
In the rhombus LMNO,
The length of the side LM = The length of the side MN = The length of the side NO = The length of the side ON
Then,
The length of the side LM = 3x - 3
The length of the side MN = x + 7
Both are equal, then the equation will be
3x - 3 = x + 7
Group the like terms
3x - x = 7 + 3
2x = 10
x = 10 /2
x = 5
Substitute the value in second equation
x + 7 = 5 + 7
= 12 units
The perimeter of the LMNO = 4 × 12
= 48 units
Hence, the perimeter of the rhombus LMNO is 48 units
The complete question is
What is the perimeter of rhombus LMNO ? A) 20 units B) 24 units C) 40 units D) 48 units
Learn more about perimeter of the rhombus here
brainly.com/question/20885093
#SPJ1

Can someone help me with this question? If I can get an equation for it and an explanation of how to do it then I should be able to do the rest of them.
The problem wants me to:
"write the equation of the parabola in intercept form."

Answers
|8|+|-7| its 15 right?
Answers
Answer:
Yes. |8|+|-7| = 15
Step-by-step explanation:
the absolute cancels out the -, so it would mean that -7 is now positive 7, so yes it'd be 15
please help!! on a time limit!

Answers
Answer:14
Step-by-step explanation:
Answer:14
Step-by-step explanation:
Suppose that on January 1 you have a balance of $ 3800 on a credit card whose APR is 16% which you want to pay off in 1 year Assume that you make no additional charges to the card after January 1. aCalculate your monthly payments bWhen the card is paid off, how much will you have paid since January What percentage of your total payment from part (b) is interest?
Answers
The monthly payment to pay off a $3800 balance on a credit card with a 16% APR in 1 year is $316.67. When the card is paid off, the total amount paid since January will be $3,800, with 0% of the payment being interest.
To calculate monthly payments, we need to determine the number of months required to pay off the card. Since the goal is to pay off the balance in 1 year, or 12 months, the monthly payment can be calculated by dividing the balance by the number of months. In this case, the monthly payment would be $316.67 ($3800/12).
To calculate the total amount paid since January, we multiply the monthly payment by the number of months. In this case, the total amount paid would be $3,800, as the balance is paid off in full.
To determine the percentage of the total payment that is interest, we need to calculate the total interest paid. This can be done by subtracting the initial balance from the total amount paid. In this case, the total interest paid would be $0 since the balance is paid off completely. Therefore, the percentage of the total payment that is interest is 0%.
In summary, the monthly payment to pay off a $3800 balance on a credit card with a 16% APR in 1 year is $316.67. When the card is paid off, the total amount paid since January will be $3,800, with 0% of the payment being interest.
For more information on credit card visit: brainly.com/question/14211445
#SPJ11
Suppose a projectile is fired from a cannon with velocity v0 and angle of elevation θ. The horizontal distance Rθ it travels (in feet) is given by the following. R(θ)=(v0)²sin2θ/32 If v0=80ft/s, what angle θ (in radians) should be used to hit a target on the ground 129 feet in front of the cannon? Do not round any intermediate computations, and round your answer(s) to the nearest hundredth of a radian. (If there is more than one answer, enter additional answers with the "or" button.)
Answers
The angle at which the projectile should be launched to hit the target which is 129 feet away is 7/100π.
The projectile fires with a velocity V₀ and angle of elevation θ, then the horizontal distance is given by the R(θ),
R(θ) = V₀²sin2θ/32
The given function in dependent on theta θ,
The angle at which the projectile must be fired so that it reaches the horizontal distance of 129 feet in front of the cannon,
R(θ) = V₀²sin2θ/32
putting R(θ) equal to 129, V₀ = 80ft/s,
129 = (80)²sin2θ/32
sin2θ = (129 x 32)/(80 x 80)
sin2θ = 0.645
Hence,
θ = 7/100π
so, the projectile should be launched at angle of 7/100π.
To know more about projectile, visit,
https://brainly.com/question/12870645
#SPJ9
Which is a degree of rotational symmetry for the regular pentagon

Answers
Explanation:
Pentagon = 5 sides.
360 degrees (degrees of a full circle) divided by 5 (sides of the pentagon) equals 72 degrees.
Please answer.
No links, no fake answers please

Answers
Answer:
The length of the side DE is approximately 541.3 feet long.
Step-by-step explanation:
There is a trigonometry law called the law of sines, which states the sine of an angle divided by its opposite side is equivalent to the sine of all the other angles in that right triangle divided by its corresponding opposite side. You can use this law to help you solve for x. By applying the law of sines, you'll get that \(\frac{sin(90^{o})}{x} =\frac{sin(10^{o})}{94}\) ⇒ \(\frac{x}{sin(90^{o})} =\frac{94}{sin(10^{o})}\) ⇒ \(x = \frac{94*sin(90^{o})}{sin(10^o)}\) ⇒ \(x=541.3ft.\)
Which answer us correct????

Answers
Answer:
the one you click is correct.
Step-by-step explanation:
A rectangular vegetable garden will have a width that is 2 feet less than the length, and an area of 48 square feet. If x represents the length, then the length can be found by solving the equation:
What is the length, x, of the garden?
Answers
Step-by-step explanation:
x = length
y = width
x×y = 48 ft²
y = x - 2
using the second in the first equation we get
x × (x - 2) = 48
x² - 2x - 48 = 0
we can solve this quickly by finding the factors of -48 that are only 2 apart in their absolute value, and the negative factor must be 2 larger in its absolute value than the positive one.
simply because
(a + b)(a - c) = a² - ac + ab - bc
-bc = -48
-ac + ab = -2x
a = x
-c + b = -2
and so we see, 48 = 6×8 (2 difference between the factors).
the larger number must be negative, so, -8×6
and we get
(x + 6)(x - 8)
therefore, the solutions are
x = -6 and x = 8
a negative length does not makes sense here, so x = 8 is or solution.
the length of the garden is 8 ft.
the width is 8 - 2 = 6 ft.
samantha used craft wire to make the design shown. she first made the smaller quadrilateral. then she enlarged the smaller quadrilateral to make the larger quadrilateral, using a scale factor that extended the 6-centimeter side by 3 centimeters. what total length of craft wire did samantha use for both quadrilaterals?
Answers
The total length of craft wire used by Samantha is 10x + 9
What is the scale factor?
A scale factor is defined as the ratio between the scale of a given original object and a new object, which is its representation but of a different size (bigger or smaller).
Let's call the length of the smaller quadrilateral's 6-centimeter side "x".
Then the length of the corresponding side in the larger quadrilateral would be 6+3=9 centimeters, since the scale factor is 3.
To find the total length of craft wire used, we need to add up the lengths of all the sides in both quadrilaterals.
The smaller quadrilateral has four sides, each with a length of x.
The larger quadrilateral also has four sides, but only one of them has a different length (9 cm), while the other three sides are simply 3 times longer than the corresponding sides in the smaller quadrilateral.
So the total length of craft wire used by Samantha is:
4x + 9 + 3x + 3x + 3x
Simplifying this expression, we get:
10x + 9
Hence, the total length of craft wire used by Samantha is:
10x + 9
To learn more about scale factor visit:
https://brainly.com/question/29967135
#SPJ4
Q5. Evaluate this expression when a=6
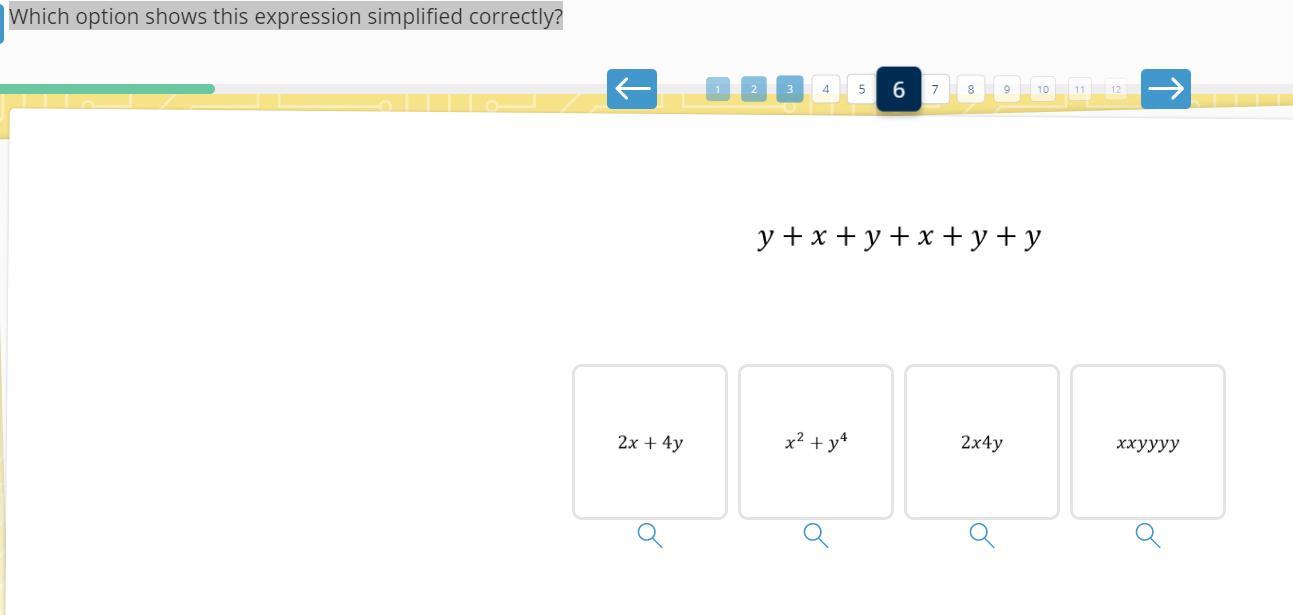
Q6. Which option shows this expression simplified correctly?
Q7. Which option shows this expression simplified correctly?
Q8. Find the following:
Q9. Which option shows this expression expanded correctly?




Answers
Question 6: 2w + 3x. There are 2 w’s, and 3 x’s.
Question 7: 2x + 4y. There are 2 x’s, and 4 y’s.
Question 8. 11 + 16 is 27.
Question 9: 3(8y - 5). 3*8y is 24y. 3*-5 is -15. The answer is 24y - 15.
Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration:) tan2(x) sec(x) dx sec(x)tan(x)ln tan(x) + "secG))) ) - = In( Isec(x) + tan(x)| ) +c
Answers
Answer:
Step-by-step explanation:
As the derivative of a constant is zero, any constant may be added to an indefinite integral (i.e., antiderivative) and will still correspond to the same integral.
Different way of stating this is that the antiderivative is a nonunique inverse of the derivative. For this reason, indefinite integrals are often written in the form
intf(x)dx=F(x)+C,
Therefore, C is an arbitrary constant known as the constant of integration.
The Wolfram Language returns indefinite integrals without constants of integration. This means that, depending on the form used for the integrand, antiderivatives F_1 and F_2 can be obtained that differ by a constant.
To know more about integration, visit:
https://brainly.in/question/46260452
#SPJ4

witch is the warmer temperature -9°F or -7°F
Answers
Answer:
-7°F
Step-by-step explanation:
At first, you might think that the answer is -9 because 9 > 7, right? Actually, the "rules" for numbers are switched when you are dealing with negative numbers. Therefore, -7 > -9 so -7°F is the correct answer.
What is the answer of 2x^2 4x 6 0?
Answers
The answer of the equation "2x^2 - 4x - 6 = 0" is -1 and 3.
The equation is solved using factorization:
2x^2 - 4x - 6 = 0 , given equation
2x^2 - 6x + 2x - 6 = 0 , factorizing
2x(x - 3) + 2 ( x - 3 ) = 0 , taking 2x common from the first two terms and 2 common from the last two terms
(2x + 2) (x - 3) = 0
now solving further
( 2x + 2 ) = 0 & ( x - 3 ) =0
2x = (0 - 2) , x = (0 + 3)
2x = (-2) , x = 3
x = (-2/2)
x = -1
Thus, the equation gives the solution as x = -1 and x = 3.
You can learn more about equation at
https://brainly.com/question/22688504
#SPJ
A telephone company charges $20 per month and $0.05 per minute for local calls. Another company charges $25 per month and $0.03 per minute for local calls. Find the number of minutes used if both charges are same.
Answers
The number of minutes used when both charges are the same is 250 minutes.
Let's assume the number of minutes used for local calls is represented by "m".
For the first telephone company, the total cost is the monthly fee of $20 plus $0.05 per minute:
Total cost for Company 1 = $20 + $0.05m
For the second telephone company, the total cost is the monthly fee of $25 plus $0.03 per minute:
Total cost for Company 2 = $25 + $0.03m
We want to find the number of minutes used when the total costs for both companies are the same. Therefore, we can set up an equation:
$20 + $0.05m = $25 + $0.03m
To solve for "m", we can simplify the equation by moving all terms with "m" to one side of the equation:
$0.05m - $0.03m = $25 - $20
0.02m = $5
Now, we can solve for "m" by dividing both sides of the equation by 0.02:
m = $5 / 0.02
m = 250
Therefore, the number of minutes used when both charges are the same is 250 minutes.
for more such question on minutes visit
https://brainly.com/question/291457
#SPJ8
Plz plz plz helpppppplllpl

Answers
Answer:
both 20 and 12 but, 12 can be more accurate. Depends on your teacher's point of view.
please mark as brainliest
A Ferris wheel is 20 meters in diameter and boarded from a platform that is 2 meters above the ground. The six o'clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 6 minutes. How much of the ride, in minutes and seconds, is spent higher than 13 meters above the ground?
Answers
Answer:
233.48s
3.84 min
Step-by-step explanation:
In order to solve this problem, we can start by drawing what the situation looks like. See attached picture.
We can model this situation by making use of a trigonometric function. Trigonometric functions have the following shape:
\(y=A cos(\omega t+\phi)+C\)
where:
A= amplitude =-20m because the model starts at the lowest point of the trajectory.
f= the function to use, in this case we'll use cos, since it starts at the lowest point of the trajectory.
t= time
\(\omega=\) angular speed.
in this case:
\(\omega=\frac{2\pi}{T}\)
where T is the period, in this case 6 min or
\(6min(\frac{60s}{1min})=360s\)
so:
\(\omega=\frac{2\pi}{360}\)
\(\omega = \frac{\pi}{160}\)
and
\(\phi\)= phase angle
C= vertical shift
in this case our vertical shift will be:
2m+20m=22m
in this case the phase angle is 0 because we are starting at the lowest point of the trajectory. So the equation for the ferris wheel will be:
\(y=-20 cos(\frac{\pi}{180}t)+22\)
Once we got this equation, we can figure out on what times the passenger will be higher than 13 m, so we build the following inequality:
\(-20 cos(\frac{\pi}{180}t)+22>13\)
so we can solve this inequality, we can start by turning it into an equation we can solve for t:
\(-20 cos(\frac{\pi}{180}t)+22=13\)
and solve it:
\(-20 cos(\frac{\pi}{180}t)=13-22\)
\(-20 cos(\frac{\pi}{180}t)=-9\)
\(cos(\frac{\pi}{180}t)=\frac{9}{20}\)
and we can take the inverse of cos to get:
\(\frac{\pi}{180}t=cos^{-1}(\frac{9}{20})\)
which yields two possible answers: (see attached picture)
so
\(\frac{\pi}{180}t=1.104\) or \(\frac{\pi}{180}t=5.179\)
so we can solve the two equations. Let's start with the first one:
\(\frac{\pi}{180}t=1.104\)
\(t =1.104(\frac{180}{\pi})\)
t=63.25s
and the second one:
\(\frac{\pi}{180}t=5.179\)
\(t=5.179(\frac{180}{\pi})\)
t=296.73s
so now we can build our possible intervals we can use to test the inequality:
[0, 63.25] for a test value of 1
[63.25,296.73] for a test value of 70
[296.73, 360] for a test value of 300
let's test the first interval:
[0, 63.25] for a test value of 1
\(-20 cos(\frac{\pi}{180}(1))+22>13\)
2>13 this is false
let's now test the second interval:
[63.25,296.73] for a test value of 70
\(-20 cos(\frac{\pi}{180}(70))+22>13\)
15.16>13 this is true
and finally the third interval:
[296.73, 360] for a test value of 300
\(-20 cos(\frac{\pi}{180}(300))+22>13\)
12>13 this is false.
We only got one true outcome which belonged to the second interval:
[63.25,296.73]
so the total time spent above a height of 13m will be:
196.73-63.25=233.48s
which is the same as:
\(233.48(\frac{1min}{60s})=3.84 min\)
see attached picture for the graph of the situation. The shaded region represents the region where the passenger will be higher than 13 m.



PLEASE HELP WILL GIVE BRANLIEST

Answers
Suppose you draw one card, put it back (and re-shuffle), and then draw another. What is the probability that the cards are of different suits
Answers
The probability that the two cards drawn are of different suits is approximately 0.3744 or 37.44%.
The probability that the first card drawn is of a particular suit (say hearts) is 13/52, because there are 13 hearts in the deck. The probability that the second card drawn is of a different suit (say diamonds) is 39/52, because there are 13 cards in each of the three remaining suits.
So, the probability that the first card is a heart and the second card is a diamond is (13/52) × (39/52) = 507/2704.
Similarly, the probability that the first card is a diamond and the second card is a heart is also (13/52) × (39/52) = 507/2704.
The probability that the two cards are of different suits is the sum of these two probabilities:
(507/2704) + (507/2704) = 1014/2704 ≈ 0.3744
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Question
Assuming you are drawing from a standard deck of 52 cards with 13 cards in each of the 4 suits (hearts, diamonds, clubs, and spades), the probability that the two cards drawn are of different suits can be calculated as follows:
Find cos x if sin x =0.82.
Answers
Answer:
cosx= 35. Use Trignometrical identity cosx = √1−sin2x . cos x = √1−1625 = √925 = 35 to be the ...
Missing: =0.82 | Must include: =0.82
Step-by-step explanation:
Top Hat Soda has 300,000 milliliters of cola to bottle. Each bottle holds 500 milliliters. How many bottles will the cola fill?
Answers
Answer:600
Step-by-step explanation:
300,000/ 500 =600
For the equation shown below, solve for \( y \) as a function of \( x \) and express the result in function notation. Use \( f \) for the name of the function. \[ -12 x+4 y=32 \] The function is
Answers
The function that represents the given equation is:
f(x) = 3x + 8
The equation is -12x + 4y = 32. To solve for y as a function of x, we need to isolate y on one side of the equation.
Adding 12x to both sides, we get 4y = 12x + 32.
To solve for y, we divide both sides of the equation by 4. This gives us y = 3x + 8.
Hence, the function that expresses y as a function of x is:
f(x) = 3x + 8.
Using this function, we can determine the value of y corresponding to any given x value. For example, if we substitute x = 5 into the function, we have f(5) = 3(5) + 8 = 15 + 8 = 23. Therefore, when x is 5, y is 23 according to the function f(x) = 3x + 8.
In summary, the function f(x) = 3x + 8 represents the relationship between x and y in the given equation, allowing us to calculate the corresponding y value for any given x value.
Therefore, the function that represents the given equation is:
f(x) = 3x + 8
Learn more about function :
https://brainly.com/question/29633660
#SPJ11