Answers
Answer:
x represents the amount of burgers you order at a restaurant and they each cost $5 y represents your total in cost of $ so if you get 3 burgers for 5 dollars each y= $15
Step-by-step explanation:
Related Questions
Marcus found these three ordered pairs for the equation y = 52x + 150: (0, 150), (10,670), and (20,1190).
When he graphs these, what is the best range for the y-axis?
0 to 150
0 to 670
0 to 20
0 to 1190

Answers
brainliest would be great:))
If triangle DEF is congruent to triangle GJH, find each missing angle?
Answers
Answer
<F = 105°
<G = 41°
<J = 34°
GJ = 19m
JH =14m
GH = 16m
Step-by-step explanation:
Since triangle DEF is congruent to triangle GJH, the following are true
<D = <G
<E = <J
<F = <H
Given
<H = 105°
Hence <F = 105°
Also <E = 34° =<J
From ∆GHJ
<G+<H+<J = 180°
<G+105+34 = 180°
<G + 139 =180
<G= 180-139
<G = 41°
Get the sides. For the sides, the following are true
DE = GJ = 19m
Also EF =JH = 14m
DF =GH = 16m

Turn this equation into a sentence: 5x - 8 - 7
Answers
Answer:
5 times x minus 8 minus 7
Step-by-step explanation:
whenever you see an x right next to a number, it means that it's being multiplied for that number. For example: 2x mean 2 times x
This symbol - is a minus symbol. So when it's in front of a number, you say "minus" and then the number. For example: 4 - 3 means, Four minus three.
Plz I need help plz

Answers
A, D, and E would have a negative product.
When multiplying two negatives together, you get a positive so B and C wouldn't work.
A manufacturer drills a hole through the center of a metal sphere of radius R = 8. The hole has a radius r. What value of r will produce a ring whose volume is exactly half the volume of the sphere? (Round your answer to two decimal places.)
Answers
Answer:
New radius(r) = 3.65 (Approx)
Step-by-step explanation:
Given:
Radius of sphere(R) = 8
Find:
New radius(r)
Computation:
Volume of sphere = (4/3)πR³
Volume of sphere = (4/3)π(6)³
Volume of sphere = 288π
Volume of ring = (4/3)π(R²-r²)³/²
Half volume of sphere = Volume of ring
288π / 2 = (4/3)π(R²-r²)³/²
144 = (4/3)(6²-r²)³/²
108 = (6²-r²)³/²
New radius(r) = 3.65 (Approx)
A private resort installed 2 additional triangular pools, as an added attraction to their clients. triangular pool abc is congruent with the triangular pool pqr. two sides of triangular pool abc and pqr measures 56 ft. and 60ft. ,while the third side of pool abc measures ( 3x 2) ft. and pool pqr measures 20ft. how can you evaluate x value?
Answers
The value of x is 8.
Triangular pool ABC is congruent to triangular pool PQR, which means that the two triangles are identical in size and shape. This means that the sides of the two triangles are in the same ratio.
Since the ratio of the sides of a triangle is determined by the angles of the triangle, the angles of triangle ABC and triangle PQR are also congruent. This means that the measures of the angles of the two triangles are equal.
Since the sides of triangle ABC have lengths 3x and 2, the third side must have a length of x. Similarly, since the sides of triangle PQR have lengths 20 and x, the third side must have a length of 20 - x.
Since triangle ABC and triangle PQR are congruent, the ratio of the lengths of their sides is the same. Therefore, we can set up the following proportion: (3x)/(2) = (20 - x)/x
Solving this proportion for x gives us:
3x = 2*(20 - x)
3x = 40 - 2x
5x = 40
x = 8
Therefore, the value of x is 8.
To learn more about Congruent Triangle,
Visit; brainly.com/question/22062407
#SPJ4
im cant figure out how to do this one ((-3)^2)^-3
Answers
Answer:
\(\dfrac{1}{729}\)
Step-by-step explanation:
\(\left(\dfrac{}{}(-3)^2\dfrac{}{}\right)^{-3}\)
First, we should evaluate inside the large parentheses:
\((-3)^2 = (-3)\cdot (-3) = 9\)
We know that a number to a positive exponent is equal to the base number multiplied by itself as many times as the exponent. For example,
\(4^3 = 4 \, \cdot\, 4\, \cdot \,4\)
↑1 ↑2 ↑3 times because the exponent is 3
Next, we can put the value 9 into where \((-3)^2\) was originally:
\((9)^{-3}\)
We know that a number to a negative power is equal to 1 divided by that number to the absolute value of that negative power. For example,
\(3^{-2} = \dfrac{1}{3^2} = \dfrac{1}{3\cdot 3} = \dfrac{1}{9}\)
Finally, we can apply this principle to the \(9^{-3}\):
\(9^{-3} = \dfrac{1}{9^3} = \boxed{\dfrac{1}{729}}\)
You are the director of the customer service center in Company Alpha. You find that the mean time between calls to the center is 6 minutes with standard deviation of 4 minutes. The effective response time is 11 minutes with a standard deviation of 20 minutes. (a) Identify the following parameters: ta
tθ
∂a
∂θ
ra:
rθ:
Answers
The identified parameters are:
ta = 6 minutes
tθ = 11 minutes
∂a = 4 minutes
∂θ = 20 minutes
ra = 1/6 minutes^(-1)
rθ = 1/11 minutes^(-1)
ta: Mean time between calls to the center
tθ: Effective response time
∂a: Standard deviation of the time between calls to the center
∂θ: Standard deviation of the effective response time
ra: Rate of calls to the center (inverse of ta, i.e., ra = 1/ta)
rθ: Rate of effective response (inverse of tθ, i.e., rθ = 1/tθ)
Given information:
Mean time between calls to the center (ta) = 6 minutes
Standard deviation of time between calls (∂a) = 4 minutes
Effective response time (tθ) = 11 minutes
Standard deviation of effective response time (∂θ) = 20 minutes
Using this information, we can determine the values of the parameters:
ta = 6 minutes
tθ = 11 minutes
∂a = 4 minutes
∂θ = 20 minutes
ra = 1/ta = 1/6 minutes^(-1)
rθ = 1/tθ = 1/11 minutes^(-1)
So, the identified parameters are:
ta = 6 minutes
tθ = 11 minutes
∂a = 4 minutes
∂θ = 20 minutes
ra = 1/6 minutes^(-1)
rθ = 1/11 minutes^(-1)
Learn more about Standard Deviation here:
https://brainly.in/question/50665860
#SPJ11
A=1/2h(c+d) solve for h
Answers
The value of h in the expression A=1/2h(c+d) is h = 2A/(c+d)
What is subject of formula?The subject of an equation is the variable that is been solved for. When you've solved an equation for the subject, your subject is the variable by itself on either the left or right side of the equation.
for example, in the equation A=1/2h(c+d), A is the subject of formula. changing the subject to h, we have to evacuate all other terms associative with h
multiplying both sides by 2
2A= h(c+d)
dividing both sides by (c+d)
therefore h= 2A/(c+d)
learn more about subject of formula from
https://brainly.com/question/21140562
#SPJ1
i need help can u help me i will give brainlyiest.

Answers
Answer:
yes
Step-by-step explanation:
hope this helps! happy new year!
The second digit of a four digit number is "0". If you write the digits of this number backwards, you will get a number 9 times bigger than the original. What is the original number?
Answers
Answer:
1089
Step-by-step explanation:
The original number is A0CD, We have that DC0A = 9 x A0CD.
If A =1, then D = 9 and we have:
9C01 = 9 x 10C9
In order for this expression to be true, the following must also be true:
(C x 9) + 8 must be divisible by 10, which means that C x 9 must end in a 2.
The only multiple of 9 (from 9 to 81) that ends in a 2 is 72.
72 = 9 x 8.
Therefore, C must be 8 and the original number is 1089. Multiply it by 9 to check the answer:
1089 x 9 = 9,081
Therefore, 1089 is correct.
Please help. This is from Algebra 2, and the answer choices are below the ‘find the area’

Answers
Answer:
5x^2 - 20
Step-by-step explanation:
(x-2)(3x+5) --> 3x^2+5x-6x-10 = 3x^2 - 1x - 10
(x-2)(2x+5) --> 2x^2+5x-4x-10 = 2x^2 + 1x - 10
3x^2 - 1x - 10 + 2x^2 + 1x - 10 = 5x^2 - 20
use gram-schmidt process on the basis {(−1, 0, 1),(1, 2, −1),(1, −2, 1)} to find an orthonormal basis for r 3 .
Answers
Tthe orthonormal basis for R³ using the Gram-Schmidt process on the given basis {(1, 1, 2), (1, 0, 3), (2, 3, 0)} is:{(1/√6, 1/√6, 2/√6), (-1/√15, -7/√15, 5/√15), (1/√245, -23/√245, 35/√245)}.
To find an orthonormal basis using the Gram-Schmidt process, follow these steps:
Step 1: Start with the given basis vectors.
v₁ = (1, 1, 2)
v₂ = (1, 0, 3)
v₃ = (2, 3, 0)
Step 2: Normalize the first vector, v₁.
u₁ = v₁ / ||v₁||
u₁ = (1, 1, 2) / √(1² + 1² + 2²)
u₁ = (1/√6, 1/√6, 2/√6)
Step 3: Compute the projection of v₂ onto u₁.
proj(v₂, u₁) = (v₂ · u₁) * u₁
where "·" denotes the dot product.
(v₂ · u₁) = (1, 0, 3) · (1/√6, 1/√6, 2/√6)
= (1/√6) + (0/√6) + (6/√6)
= 7/√6
proj(v₂, u₁) = (7/√6) * (1/√6, 1/√6, 2/√6)
= (7/6, 7/6, 14/6)
Step 4: Compute the orthogonal vector, v₂ - proj(v₂, u₁).
w₂ = v₂ - proj(v₂, u₁)
w₂ = (1, 0, 3) - (7/6, 7/6, 14/6)
w₂ = (1 - 7/6, 0 - 7/6, 3 - 14/6)
w₂ = (-1/6, -7/6, 5/6)
Step 5: Normalize the orthogonal vector, w₂.
u₂ = w₂ / ||w₂||
u₂ = (-1/6, -7/6, 5/6) / √((-1/6)² + (-7/6)² + (5/6)²)
u₂ = (-1/√15, -7/√15, 5/√15)
Step 6 : Compute the projection of v₃ onto u₁ and u₂.
proj(v₃, u₁) = (v₃ · u₁) * u₁
proj(v₃, u₂) = (v₃ · u₂) * u₂
(v₃ · u₁) = (2, 3, 0) · (1/√6, 1/√6, 2/√6)
= (2/√6) + (3/√6) + (0/√6)
= 5/√6
(v₃ · u₂) = (2, 3, 0) · (-1/√15, -7/√15, 5/√15)
= (-2/√15) + (-21/√15) + (0/√15)
= -23/√15
proj(v₃, u₁) = (5/√6) * (1/√6, 1/√6, 2/√6)
= (5/6, 5/6, 10/6)
proj(v₃, u₂) = (-23/√15) * (-1/√15, -7/√15, 5/√15)
= (23/15, 161/15, -115/15)
Step 7: Compute the orthogonal vector, v₃ - proj(v₃, u₁) - proj(v₃, u₂).
w₃ = v₃ - proj(v₃, u₁) - proj(v₃, u₂)
w₃ = (2, 3, 0) - (5/6, 5/6, 10/6) - (23/15, 161/15, -115/15)
w₃ = (2 - 5/6 - 23/15, 3 - 5/6 - 161/15, 0 - 10/6 + 115/15)
w₃ = (1/30, -23/30, 35/30)
Step 8: Normalize the orthogonal vector, w₃.
u₃ = w₃ / ||w₃||
u₃ = (1/30, -23/30, 35/30) / √((1/30)² + (-23/30)² + (35/30)²)
u₃ = (1/√245, -23/√245, 35/√245)
u₃ = (1/√245, -23/√245, 35/√245)
Therefore, the orthonormal basis for R³ using the Gram-Schmidt process on the given basis {(1, 1, 2), (1, 0, 3), (2, 3, 0)} is:
{(1/√6, 1/√6, 2/√6), (-1/√15, -7/√15, 5/√15), (1/√245, -23/√245, 35/√245)}.
To know more about orthogonal check the below link:
https://brainly.com/question/31629623
#SPJ4
whats 4 1/12-1/2 ASAP PLEASE
Answers
Answer:
4
Step-by-step explanation:
4 1/2 - 1/2
4
You start with 4 + 1/2 but you subtract 1/2 so it just cancel's itself out leaving you with 4.
Hope this helps! If you have any additional questions please don't hesitate to ask me or your teacher to be sure you master the subject. Stay safe and please mark brainliest! :)
Answer:
\(3 \frac{7}{12}\)
Step-by-step explanation:
1 - multiply the 1/2 out to make the denominators the same (Ignore the 4 for now)
To make 2 equal 12 you multiply by 6 and what you do to the bottom you do to the top.
\(\frac{1}{2}(\frac{6}{6}) = \frac{6}{12}\)
2 - Now solve
Now we need to know what 4 1/12 - 6/12 equals.
1-6 is -5 so we will take out of the whole number to continue this subtraction
3 12/12 - 5/12
After subtracting that out we're left with
3 7/12
Hope this helps :)
$86 for 8 hours of babysitting. how much do u make for one hour?
unit rate :
plz help meee
Answers
50 POINTS!!!!! SPAM ANSWERS WILL BE REPORTED! GIVE ANSWER AND SHOW WORK PLEASE!!! THANKS!!!!!!!

Answers
Answer:
Question 12: Find the slope from these two points: (-3,-3) and (-4,-8)
The formula for finding the slope from two points is attached to this answer.
So if we plug in our values that correspond to the formula we get the following:
First pair: -3 is our x1, -3 is our y1,
Second pair: -4 is our x2, -8 is our y2
-8--3/-4--3
-8+3/-4+3
-5/-1=5, Our slope is 5 for question 12
Question 18: Find the area of a circle with a diameter of 31.
Area=\(\pi r^2\)
So we have \(15.5^{2} \pi\)
240.25 times 3.14 is 754.385, if we round to the nearest whole number we receive 754 as our answer for question 18
Question 21: Find the measurement of a missing leg in a right triangle when given the hypotenuse and another leg
We know that the hypotenuse is 8cm and one of the legs is 5cm
the formula would be \(a^{2} +b^{2}= c^{2}\) for the hypotenuse but this can be used to find the missing legs as well.
\(5^{2} +b^{2} =8^{2}\)
\(25+b^{2} =64\)
Subtract 25
\(b^{2} =39\)
b would equal 6.44 something but the question said to round to the nearest whole number which would be 6.
Question 23: Find the volume of a cone
Radius: 10, height: 7
Formula to find the volume of a cone: 1/3 times 3.14 times r^2 times the height
1/3 times 3.14 times 10^2 times 7
1/3 times 3.14 times 700
1.046 (the 46 is repeating) repeating times 700
732.06 repeating, the 6 is repeating.
The question also asks us to round to the nearest whole number so the answer to question 23 would be 733
Question 26: Find the volume of a sphere
Radius is 6 and pi is 3.14
Formula: \(4\pi \frac{r^3}{3}\)
So we have 4 times 3.14 times 6^3 divided by 3
4 times 3.14 times 108/3
4 times 3.14 times 36
12.56 times 36
452.16, I didn't see this answer listed on your worksheet, so please correct me if I'm wrong
Question 47: Probability of a number cube rolled many times to see how many times an even number is rolled.
Since this is a standard number cube there must be 6 sides, therefore half the numbers are even so
65 * 2 = 32.5, which rounds up to 33
33 is our answer to question 47
Hope I helped, have a nice day :)
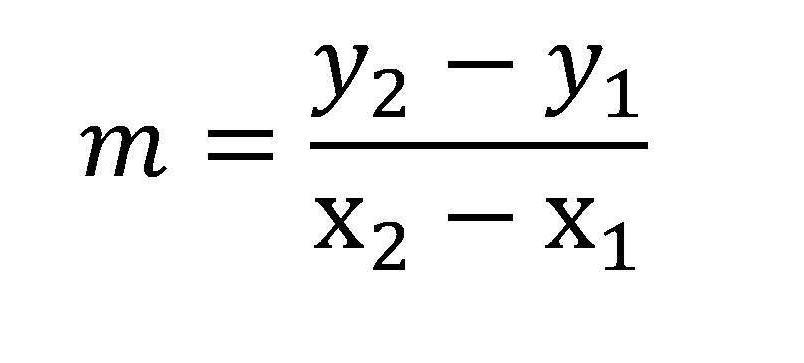
The measure of angle 1 is 65 degrees. What are the measures of the other seven angles? (Enter the
number only)
Help I need big brains for it and I need it fast please help please

Answers
Answer:
See solution below
Step-by-step explanation:
According to the diagram shown
m<1 = m<5 = 5=65 degrees (corresponding angle)
m<5 = m<4 - 65 degrees (alternate interior angle)
m<9 = m<8 = 65degrees (corresponding angle)
m<5 = m<8 = 65dgrees (vertically opposite angles)
m<6+m<8 = 180
m<6 + 65 = 180
m<6 = 180 - 65
m<6 = 115degrees
m<2 = m<6 = 115degrees (corresponding angles)
m<6 = m<7 = 115degrees (vertically opposite angles)
m<3 = m<7 = 115degrees(corresponding angle)
)
The measures of the other seven angles are evaluated as:
\(m\angle 1 = 65^\circ = m\angle 5\\m\angle 2 =115^\circ = m\angle 6\\m\angle 3 =65^\circ = m\angle 7\\m\angle 4 = 115^\circ =m\angle 8\)
What are supplementary angles?Two angels whose sum is 180° are called supplementary angles.
When they are added together graphically, they form a straight line.
What are vertical angles?Each of the pairs of the opposite angles made by two intersecting lines are called vertical angles. They are of same measurement.
What are corresponding angles?In literal sense, corresponding means pair wise angles. Like the right corner angles of two triangles etc. But usually we take them as:
For two similar figures, the pair by pair similar angles of those two similar figures are called corresponding angles. They are of same measurement.
For this case, we have:
Angle 1,2,3 and 4 corresponding to 5,6,7 and 8 angle respectively. It is because the two lines A and B are parallel and the traversing line intersects both of them. When single line intersect two parallel lines, it makes same corresponding angles on both of the sides. That means
\(m\angle 1 = m\angle 5\\m\angle 2 = m\angle 6\\m\angle 3 = m\angle 7\\m\angle 4 = m\angle 8\)
where that small 'm' denotes that we're taking about their measurements.
Thus, we will only find 1,2,3,and angle 4's measurements and rest four would be found.
Since angle 1 and angle 4 are vertical angles, they are same measurement. Since angle 1 is of 65 degrees, thus:
\(m\angle 1 = 65^\circ = m\angle 4\)
Now, since angle angle 3 is supplementary to angle 1 and so as angle 2 to angle 4, thus:
\(m\angle 2 + m\angle 4 = 180^\circ\\m\angle 2 = 180-m\angle 4= 115^\circ\\\\m\angle 3 + m\angle 1 = 180^\circ\\m\angle 3 = 180-m\angle 1= 115^\circ\)
Thus, we get the measurement of all angles as:
\(m\angle 1 = 65^\circ = m\angle 5\\m\angle 2 =115^\circ = m\angle 6\\m\angle 3 =65^\circ = m\angle 7\\m\angle 4 = 115^\circ =m\angle 8\)
Learn more about corresponding angles here:
https://brainly.com/question/23134162
subway sells foot long sandwiches that have a mean of 11 inches and a standard deviation of .5 inches. 20% of sandwiches are less than inches. (the cumulative standardized normal distribution table indicates a z value of -.84 for 20%) 11.500 11.42 10.58 cannot be determined from the information given
Answers
using standard z value, 20% of sandwiches are less than 10.58 inches.
In the given question,
Subway sells foot long sandwiches that have a mean of 11 inches and a standard deviation of 0.5 inches.
20% of sandwiches are less than...............inches.
The cumulative standardized normal distribution table indicates a z value of -0.84 for 20%.
From the question we know that
Mean(μ) = 11 inches
Standard Deviation(σ) = 0.5 inches
We have to find less than of 20% of sandwiches for z value of -0.84
P(ƶ<z) = 20%
We can write it as
P(ƶ<-0.84) = 20/100
P(ƶ<-0.84) = 0.20
Since z = -0.84
X-μ/σ = -0.84
Now putting the value
X-11/0.5 = -0.84
Multiply by 0.5 on both side
X-11/0.5 *0.5= -0.84*0.5
X-11= -0.42
Add 11 on both side
X-11+11= -0.42+11
X = 10.58
Hence, 20% of sandwiches are less than 10.58 inches.
To learn more about standard z value link is here
https://brainly.com/question/27315585
#SPJ4
Right question is here
Subway sells foot long sandwiches that have a mean of 11 inches and a standard deviation of 0.5 inches. 20% of sandwiches are less than ................. inches. (The cumulative standardized normal distribution table indicates a z value of -.84 for 20%)
(a) 11.500
(b) 11.42
(c) 10.58
(d) cannot be determined from the information given
Meghan has y dollars.
Joseph has half as much money as Meghan.
Which expression represents the amount of money Joseph has?
Answers
If Meghan has y dollars and Joseph has half as much money as Meghan then the expression y ÷ 2 represents the amount of money Joseph has. Thus, the most appropriate option which is the answer to the given question is B.
An expression is defined as a mathematical phrase with two or more variables with any of the mathematical operations between them. The following are a few examples of expressions: 3x + 45y, 9u, 55 - a, and so on.
In the given question, We are given,
Amount of money Meghan has = $y
Amount of money Joseph has = half as much as Meghan
Thus to calculate the money owned by Joseph, we have to divide the money of Meghan by 2.
And we get the amount of money Joseph has = y ÷ 2
Learn more about Expressions:
https://brainly.com/question/25968875
#SPJ4
The complete question might have been:
Meghan has y dollars. Joseph has half as much money as Meghan. Which expression represents the amount of money Joseph has?
A. y + 2
B. y * 2
C. y ÷ 2
D. y - 2
Given: -4x + 2y = 8
Prove: y = 4 + 2x
Answers
Answer:
Step-by-step explanation:
-4x+2y=8
2y=8+4x
y=\(\frac{8+4x}{2}\)
y=\(\frac{2(4+2x)}{2}\)
y=4+2x
proved
1/2 divided by blank = 1/8 because 1/8 x blank = 1/2
Answers
Answer:
blank is 4
Step-by-step explanation:
We can set up the equation:
\(\frac{1}{8} *x = \frac{1}{2}\)
To solve, multiply both sides by 8.
\(\frac{1}{2}*8 = 4\)
This checks out with the other statement.
This extreme value problem has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint.
f(x, y, z) = 6x + 6y + 5z; 3x2 + 3y2 + 5z2 = 29
Max value ________
Min value ____________
Answers
The max value and min value can then be determined from these critical points.
To find the extreme values of a function subject to a constraint, we can use Lagrange multipliers. First, we set up the Lagrangian equation by multiplying the constraint by a scalar λ and adding it to the original function.
Then, we take the partial derivatives of the Lagrangian equation with respect to each variable and set them equal to zero. This will give us a system of equations to solve for the critical points.
Once we have the critical points, we need to determine which ones are maximums and which are minimums.
To do this, we can use the second derivative test. If the second derivative is positive at a critical point, it is a minimum. If the second derivative is negative, it is a maximum.
In summary, to find the extreme values of a function subject to a constraint using Lagrange multipliers, we set up the Lagrangian equation, solve for the critical points, and then use the second derivative test to determine which ones are maximums and which are minimums.
To learn more about : max value
https://brainly.com/question/30236354
#SPJ11
The maximum value of f(x, y, z) is 26.5, and the minimum value is -29.
How did we get the values?To find the extreme values of the function f(x, y, z) = 6x + 6y + 5z subject to the constraint 3x² + 3y² + 5z² = 29 using Lagrange multipliers, set up the following system of equations:
1. ∇ f = λ∇g
2. g(x, y, z) = 3x² + 3y² + 5z² - 29
where ∇f and ∇g are the gradients of f and g respectively, and λ is the Lagrange multiplier.
Taking the partial derivatives, we have:
∇ f = (6, 6, 5)
∇g = (6x, 6y, 10z)
Setting these two gradients equal to each other, we get:
6 = 6λx
6 = 6λy
5 = 10λz
Dividing the first two equations by 6\(\lambda\), we obtain:
x = ¹/λ
y = ¹/λ
Substituting these values into the third equation, we have:
5 = 10λz
z = ¹/2λ
Now, substitute x, y, and z back into the constraint equation to find the value of λ:
3(¹/λ)² + 3(¹/λ)² + 5(1/2λ)² = 29
6(¹/λ²) + 5(⁴/λ²) = 29
24 + 5 = 116λ²
116λ² = 29
λ² = ²⁹/₁₁₆
λ = ±√²⁹/₁₁₆
λ = ± √²⁹/2√29
λ = ± ¹/₂
We have two possible values for λ, λ = ¹/₂ and λ = ¹/₂
Case 1: λ = ¹/₂
Using this value of λ, we can find the corresponding values of x, y, and z:
x = ¹/λ = 2
y =¹/λ = 2
z = 1/2 λ = ¹/₂
Case 2: λ = -1/2
Using this value of λ, find the corresponding values of x, y, and z:
x = 1/λ = -2
y = 1/λ = -2
z = 1/(2λ) = -1
Now that we have the values of x, y, and z for both cases, substitute them into the objective function f(x, y, z) to find the extreme values.
For Case 1:
f(x, y, z) = 6x + 6y + 5z
= 6(2) + 6(2) + 5(1/2)
= 12 + 12 + 2.5
= 26.5
For Case 2:
f(x, y, z) = 6x + 6y + 5z
= 6(-2) + 6(-2) + 5(-1)
= -12 - 12 - 5
= -29
Therefore, the maximum value of f(x, y, z) is 26.5, and the minimum value is -29.
learn more about Lagrange multipliers: https://brainly.com/question/4609414
#SPJ4
the perimeter of a right angle triangle is 24 cm and its area is 24 cm square if the hypotenuse is 13 cm find the remaining sides
Answers
Answer:
let the remaining sides be X and Y
perimeter = X + Y + 13
24 = X + Y + 13
11 = X + Y ---(1).
Area = 1/2 * base * height
24 = 1/2 * X * Y
XY = 48.-----(2)
solving eq 1 and 2
X + Y = 11
XY = 48
Xy + y² = 11y
Xy = 48
y²= 11y - 48
y² -11y + 48 = 0
no real solution of this equation.
Answer:
Step-by-step explanation:
the triangle is NOT a 3–4–5 or multiple,
so it is not a right triangle or your data is wrong.
At a town fair, everyone who wins one of the contests selects a prize. There are 14 prizes available, including 7 pies, 4 gift certificates, 2 fruit baskets, and 1 bicycle. (Suppose all prizes are equally valuable to each conestant.)
What is the probability that the first 3 winners will all select gift certificates?
What is the probability that the first winner will select either a pie or a fruit basket?
Answers
Problem 1
A = probability 1st winner picks gift certificate (no replacement)
A = 4/14 = 2/7
B = probability 2nd winner picks gift certificate (no replacement)
B = 3/13
C = probability 3rd winner picks gift certificate (no replacement)
C = 2/12 = 1/6
D = probability first 3 winners pick gift certificate (no replacement)
D = A*B*C
D = (2/7)*(3/13)*(1/6)
D = (2*3*1)/(7*13*6)
D = 6/546
D = 1/91 is the final answer
======================================================
Problem 2
A = probability 1st winner picks pie
A = 7/14
B = probability 1st winner picks fruit basket
B = 2/14
C = probability 1st winner picks pie OR fruit basket
C = A+B
C = 7/14 + 2/14
C = 9/14 is the final answer
About 80% of the precipitation that enters Crater Lake falls directly on the surface of the lake. Write this percent as a decimal.
80% =
Answers
Answer: 0.80
Step-by-step explanation:
Given
80% of the precipitation falls on the lake surface
The percentage can be written as
\(x\%=\dfrac{x}{100}\)
\(\therefore 80\%=\dfrac{80}{100}=0.80\)
I NEED HELP!!!!!!
Workers install 840 chairs at a constant rate. After 5 days, the workers still have to install 240 chairs. How much time does it take to install the chairs from start to finish?
Answers
Let's call the time it takes to install all the chairs from start to finish "t". The workers install 840 chairs per day, so in "t" days they will have installed 840 * t chairs.
At the end of 5 days, they still have 240 chairs to install, so they have installed 840 * 5 chairs so far. We can use this information to write an equation:
840 * t - 840 * 5 = 240
Expanding and simplifying the equation gives us:
840t - 4200 = 240
Adding 4200 to both sides gives us:
840t = 4440
Finally, dividing both sides by 840 gives us:
t = 5.2857142857...
So it takes approximately 5.29 days to install all the chairs from start to finish.
NEED HELP ASAP what function is this??

Answers
Answer:
linear
Step-by-step explanation:
the graph in the above equation is linear function
A student writes the equation for a line that has a slope of -6 and passes through the point (2, –8).
y -(-8) = -6(x - 2)
y -(-8) = -6x + 12
y -(-8) + 8 = -6x + 12 + 8
y = -6x + 20
Explain why the work is not correct.
(it has to be in a sentence or paragraph!)
Answers
Find measure of angles B, E, D and C and the length of BC.
Triangle ABC ~ Triangle DEF. Measure of angle A = 30 degrees and measure of angle F = 65 degrees. AB=20, DE = 35, EF= 28.

Answers
Answer:
< B = 180-30-65=85°
< E = 85°
< D = 30°
< C = 65°
BC = 20/35 × 28 = 16
Answer:
<D = 30
< C = 65
<B = <E = 85
16 = BC
Step-by-step explanation:
ABC ~ Triangle DEF
<A = <D = 30
< C = <F = 65
Since they are similar triangles
A+ C + B = 180 since the angles of a triangle = 180
30+65+B =180
95+ B = 180
<B = 180 -95 = 85
<B = <E = 85
The triangles are similar so the sides are proportional
AB BC
---- = ---------
DE EF
20 BC
---- = ---------
35 28
Using cross products
20*28 = 35 BC
Divide each side by 35
20*28/35 = 35/35 BC
16 = BC
is anyone expert here in data forecasting methods? I need some help in some topics like time series(holts, holts winter), naive method, regression, acf, pacf, arima, stl method and multivariate time series. please reply if you can help me with these topics
Answers
Yes, there are experts here in data forecasting methods who can help you with the topics you've mentioned including time series (holts, holts winter), naive method, regression, acf, pacf, arima, stl method and multivariate time series.
Below are brief explanations of each of these terms:
Time Series: A time series is a sequence of observations of a particular quantity measured over time. Holts Method: The Holt’s method is a forecasting method that forecasts the data by taking into account the trend component along with the level component. Holts Winter Method: Holt's winter model is used to forecast seasonal univariate time series.Naive Method: The naive method is a forecasting method that uses the most recent observation as a forecast for the next time period.Regression: Regression is a statistical method used to estimate the strength and direction of the relationship between two or more variables.ACF & PACF: Autocorrelation function (ACF) and partial autocorrelation function (PACF) are statistical tools used to determine the nature of the correlation between a variable and its lag.ARIMA: ARIMA stands for AutoRegressive Integrated Moving Average. ARIMA is a forecasting technique that uses past data points to predict future values.STL Method: STL is a time series decomposition method that separates a time series into three components: trend, seasonality, and random.Multivariate Time Series: Multivariate time series analysis deals with the analysis of time series data that involves more than one variable.Based on the topics you've mentioned, you may want to ask specific questions regarding these topics to get more detailed answers.To know more about data forecasting, visit
https://brainly.com/question/28431229
#SPJ11
