Answers
9514 1404 393
Answer:
c = 7d = 5Step-by-step explanation:
When a value is moved from outside the radical to inside, it gets an exponent equal to the index of the radical.
A) x³√x = √(x^(2·3+1)) = √(x^7) . . . . c = 7
__
B) x∛(x²) = ∛(x^(3·1+2)) = ∛(x^5) . . . . d = 5
_____
Alternate solution
You could use the fractional exponent equivalent of the radical and write the sum of exponents equation.
A) c/2 = 3+1/2 ⇒ c = 7 . . . . . exponents for x
B) d/3 = 1+2/3 ⇒ d = 5 . . . . . exponents for x
__
The exponent rules being used here are ...
√x = x^(1/2)
∛x = x^(1/3)
(x^a)(x^b) = x^(a+b)
(x^a)^b = x^(ab)
Related Questions
The table below represents a frequency distribution for the age (in years) of employees at a particular company.
Age (in years) Frequency
23-29
25
30-36
41
37-43
37
Use the table to answer the following questions.
Your answers should be exact numerical values
The class width used for the frequency distribution is
The class midpoint for the class 23-29 is
The class midpoint for the class 30-36 is
The class midpoint for the class 37-43 is
Check
Answers
The class width used for the frequency distribution is 6.
The class midpoint for the class 23-29 is 26.
The class midpoint for the class 30-36 is 33.
The class midpoint for the class 37-43 is 40.
To find the class width of the frequency distribution, we need to determine the range of each age class. The range is the difference between the upper and lower boundaries of each class. Looking at the table, we can see that the class boundaries are as follows:
23-29
30-36
37-43
For the class 23-29, the lower boundary is 23 and the upper boundary is 29. To find the class width, we subtract the lower boundary from the upper boundary:
Class width = 29 - 23 = 6
So, the class width for the frequency distribution is 6.
To find the class midpoint for each class, we take the average of the lower and upper boundaries of each class.
For the class 23-29:
Class midpoint = (23 + 29) / 2 = 52 / 2 = 26
For the class 30-36:
Class midpoint = (30 + 36) / 2 = 66 / 2 = 33
For the class 37-43:
Class midpoint = (37 + 43) / 2 = 80 / 2 = 40
So, the class midpoint for the class 23-29 is 26, for the class 30-36 is 33, and for the class 37-43 is 40.
For more such questions on class width visit:
https://brainly.com/question/30459609
#SPJ8
What ratio is equivalent to 3:9?
Answer choices:
24:54
18:54
36:81
Answers
Answer:
18 to 54
Step-by-step explanation: 3 times 6 is 18 and 9 times 6 is 54. These 2 are ratios equal to 3 to 9. I hope this helps brudda :D
A class contains 5 girls and 7 boys. Two are selected for a class committee. What is the probability that a girl and boy are selected?
Answers
The probability of selecting a girl and a boy for the class committee can be calculated by considering the total number of outcomes and the number of favorable outcomes.
Identify the number of girls and boys in the class. In this case, there are 5 girls and 7 boys.
Determine the total number of students in the class. That is 5 + 7 = 12.
Determine the number of ways to select two students from the class.
Here we can use the combination formula, which is written as C(n, r), where n is the total number of items and r is the number of items to be chosen.
In our case, n = 12 (total number of students) and r = 2 (number of students to be selected).
C(12, 2) = 12! / (2!(12-2)!) = 66.
Determine the number of favorable outcomes.
In this case, we want to select one girl and one boy. We multiply the number of girls by the number of boys: 5 x 7 = 35.
To find the probability, we divide the number of favorable outcomes (35) by the total number of outcomes (66):
Probability = Number of favorable outcomes / Total number of outcomes = 35 / 66 = 5/6.
So, the probability of selecting a girl and a boy for the class committee is 5/6.
Read more about probability,
https://brainly.com/question/30390037
Dominic has $0.88 worth of pennies and nickels. He has a total of 28 pennies and nickels altogether. Determine the number of pennies and the number of nickels that Dominic has.
Answers
Answer:
13 pennies and 15 nickels
Step-by-step explanation:
Let the number of pennies be p and the number of nickels be n.
\(n+p=28 \\ \\ 0.01p+0.05n=0.88 \implies p+5n=88 \\ \\ \implies 4n=60 \longrightarrow n=15 \\ \\ \therefore 15+p=28 \implies p=13\)
What is the standard form equation of an ellipse that has vertices (−2,−18) and (−2,8) and foci (−2,−14) and (−2,4)?
Answers
Answer:
Hello,
Step-by-step explanation:
All is in the picture.
B=(-2,8), O=(-2,-5)
b=BO=8+5=13
F_1=(-2,4) O=(-2,5) Focus distance=4+5=9
Horizontal half axis=√(b²-f²)=√88

What is the equation of the line?

Answers
Answer:
y=1/2x+2
Step-by-step explanation:
I found this out just by looking at the line
Helpp im being timedd

Answers
Which ones right ????

Answers
please help me answer the rest

Answers
The following are composite functions and their domains:
a. (f∘g)(1) = -1
b. (f∘g)(-1) = -1
c. (g∘f)(-1) = 2
d. (g∘f)(0) = 0
e. (g∘g)(-2) = 2
f. (f∘f)(-1) = -3
What is composite function?A function is composite when the co- domain of the first mapping is the domain of the second mapping
For the functions f(x) ang g(x) defined for the values of x in the table, we shall evaluate for the domain the composite functions as follows:
g(1) = 0, then (f∘g)(1) = -1
g(-1) = 0 ,then (f∘g)(-1) = -1
f(-1) = -2 , then (g∘f)(-1) = 2
f(0) = -1, then (g∘f)(0) = 0
g(-2) = 2, then (g∘g)(-2) = 2
f(-1) = -2 , then (f∘f)(-1) = -3
Therefore, the domain of the composite functions (f∘g)(1), (f∘g)(-1), (g∘f)(-1), (g∘f)(0), (g∘g)(-2), and (f∘f)(-1) are: -1, -1, 2, 0, 2, and -3 respectively.
Know more about composite function here:https://brainly.com/question/10687170
#SPJ1
Me ayudais por favor

Answers
Answer:
x= - 52
Step-by-step explanation:
we need to multiply both sides by 4 to leave the x alone
so
\(\frac{-x}{4} *4= 13*4\\-x= 52\\\frac{-x}{-1}=\frac{52}{-1}\\ x=-52\)
Divide. −3.52−2.2 What is the quotient
Answers
The quotient of - 3.32 / - 2.2 is 8 ÷5.
What is the quotient?Given fraction:
-3.32 / -2.2
First step is to re-write the given fraction which is - 3.52 / - 2.2
3.52 / 2.2
Second step is to convert the decimal to fraction
352 ÷ 100 / 22 ÷10
Third step is to reduce the fraction
reducing 352/100
=(2^5 × 11)/(2^2 × 5^2)
= [(2^5 × 11) ÷ 2^2] / [(2^2 × 5^2) ÷ 2^2]
= (2^3 × 11)/5²
= 88/25
Reducing 22/10
Divide the numerator and denominator by the greatest common divisor
= 22 ÷ 2 / 10 ÷ 2
= 11 /5
Now let determine or find the quotient
88 ÷ 25 × 11 ÷ 5
= 8 ÷ 5
Therefore we can conclude that 8 ÷ 5 is the quotient.
Learn more about quotient here: https://brainly.com/question/11418015
#SPJ1
Which table represents the graph of a logarithmic function in the form y = log, when b > 1?хV-31814-2-11102.1ху-1.9--2.096-1.75--1.262

Answers
The given equation is
\(\begin{gathered} y=log_bx \\ \text{where b > 1} \end{gathered}\)To know which of the options is the answer we substitute for x and y independently in the equation
For the graph, the values of the first option agrees with a value for b > 1
\(\begin{gathered} -3=1og_b\frac{1}{8} \\ b^{-3}=\frac{1}{8} \\ b^{-3}=2^{-3} \\ b\text{ =2} \end{gathered}\)Again
\(\begin{gathered} \text{if y=}1\text{ and x =}2 \\ 1=\log _b2 \\ b^1=2 \\ b\text{ =2} \end{gathered}\)So the answer is option A
Negative X to the power of three times negative X to the power four times negative X to the power five
Answers

I don't need lengthy details I just want the answer

Answers
Answer:
Sue rode 1885 miles total
Step-by-step explanation:
There are 31 days in March, 30 in April, and 30 in May.
31 * 12 + 30 * 12 + 30 * 12 = 1092
There are 30 days in June and 31 in august.
30 * 13 + 31 * 13 = 793
Now we find the total:
1092 + 793 = 1885
6. Journalise the following transactions
1. Bricks for Rs 60,000 and timber for Rs 35,000 purchased for
the construction of building. The payment was made by cheque.
2. Placed in fixed deposit account at bank by transfer from current
account Rs 13,000.
3. Appointed Mr. S.N. Rao as Accountant at Rs 300 p.m. and
Received Rs 1000 as security Deposit at 5% p.a. interest.
4. Sold goods to shruti for Rs 80,000 at 15% trade discount and
4% cash discount. Received 75% amount immediately through a
cheque.
5. Purchased goods from Richa for Rs 60,000 at 10% trade
discount and 5% cash discount. 60% amount paid by cheque
immediately.
6.
On 18th jan,Sold goods to shilpa at the list price of Rs 50,000
20% trade discount and 4% cash discount if the payment is made
within 7 days. 75% payment is received by cheque on Jan 23rd.
7. On 25th jan, sold goods to garima for Rs 1,00,000 allowed her
20% trade discount and 5% cash discount if the payment is made
within 15 days. She paid 1/4th of the amount by cheque on Feb 5th
and 60% of the remainder on 15th in cash.
8. Purchased land for Rs 2,00,000 and paid 1% as brokerage and
Rs 15,000 as registration charges on it. Entire payment is made by
cheque.
9. Goods worth Rs 25,000 and cash Rs 40,000 were taken away
by the proprietor for his personal use.
10. Sold goods costing Rs 1,20,000 to charu at a profit of 33% 3 %
on cost less 15% trade discount.
9
11. Paid rent of building Rs 60,000 by cheque. Half the building is
used by the proprietor for residential purpose.
12. Sold goods costing Rs 20,000 to sunil at a profit of 20% on
sales less 20% trade discount .
13. Purchased goods for Rs 1000 from nanda and supplied it to
helen for Rs 1300. Helen returned goods worth Rs 390, which in
turn were returned to nanda.
14. Received invoice at 10% trade discount from rohit and sons
and supplied these goods to madan, listed at Rs 3000.
Answers
1.Bricks and timber purchased for construction. (Debit: Bricks - Rs 60,000, Debit: Timber - Rs 35,000, Credit: Bank - Rs 95,000)
2.Transfer of Rs 13,000 to fixed deposit account. (Debit: Fixed Deposit - Rs 13,000, Credit: Current Account - Rs 13,000)
3.Appointment of Mr. S.N. Rao as Accountant. (Debit: Salary Expense - Rs 300, Debit: Security Deposit - Rs 1,000, Credit: Accountant - Rs 300)
4.Goods sold to Shruti with discounts. (Debit: Accounts Receivable - Shruti - Rs 80,000, Credit: Sales - Rs 80,000)
5.Goods purchased from Richa with discounts. (Debit: Purchases - Rs 60,000, Credit: Accounts Payable - Richa - Rs 60,000)
6.Goods sold to Shilpa with discounts and received payment. (Debit: Accounts Receivable - Shilpa - Rs 50,000, Credit: Sales - Rs 50,000)
7.Goods sold to Garima with discounts and received partial payment. (Debit: Accounts Receivable - Garima - Rs 1,00,000, Credit: Sales - Rs 1,00,000)
8.Purchase of land with additional charges. (Debit: Land - Rs 2,00,000, Debit: Brokerage Expense - Rs 2,000, Debit: Registration Charges - Rs 15,000, Credit: Bank - Rs 2,17,000)
9.Proprietor took goods and cash for personal use. (Debit: Proprietor's Drawings - Rs 65,000, Credit: Goods - Rs 25,000, Credit: Cash - Rs 40,000)
10.Goods sold to Charu with profit and discount. (Debit: Accounts Receivable - Charu - Rs 1,20,000, Credit: Sales - Rs 1,20,000)
11.Rent paid for the building. (Debit: Rent Expense - Rs 60,000, Credit: Bank - Rs 60,000)
12.Goods sold to Sunil with profit and discount. (Debit: Accounts Receivable - Sunil - Rs 24,000, Credit: Sales - Rs 24,000)
13.Purchased goods from Nanda and supplied to Helen. (Debit: Purchases - Rs 1,000, Debit: Accounts Payable - Nanda - Rs 1,000, Credit: Accounts Receivable - Helen - Rs 1,300, Credit: Sales - Rs 1,300)
14.Purchased goods from Rohit and Sons and supplied to Madan. (Debit: Purchases - Rs 2,700, Credit: Accounts Payable - Rohit and Sons - Rs 2,700, Debit: Accounts Receivable - Madan - Rs 3,000, Credit: Sales - Rs 3,000)
Here are the journal entries for the given transactions:
1. Bricks and timber purchased for construction:
Debit: Bricks (Asset) - Rs 60,000
Debit: Timber (Asset) - Rs 35,000
Credit: Bank (Liability) - Rs 95,000
2. Transfer to fixed deposit account:
Debit: Fixed Deposit (Asset) - Rs 13,000
Credit: Current Account (Asset) - Rs 13,000
3. Appointment of Mr. S.N. Rao as Accountant:
Debit: Salary Expense (Expense) - Rs 300
Debit: Security Deposit (Asset) - Rs 1,000
Credit: Accountant (Liability) - Rs 300
4. Goods sold to Shruti:
Debit: Accounts Receivable - Shruti (Asset) - Rs 80,000
Credit: Sales (Income) - Rs 80,000
5. Goods purchased from Richa:
Debit: Purchases (Expense) - Rs 60,000
Credit: Accounts Payable - Richa (Liability) - Rs 60,000
6. Goods sold to Shilpa:
Debit: Accounts Receivable - Shilpa (Asset) - Rs 50,000
Credit: Sales (Income) - Rs 50,000
7. Goods sold to Garima:
Debit: Accounts Receivable - Garima (Asset) - Rs 1,00,000
Credit: Sales (Income) - Rs 1,00,000
8.Purchase of land:
Debit: Land (Asset) - Rs 2,00,000
Debit: Brokerage Expense (Expense) - Rs 2,000
Debit: Registration Charges (Expense) - Rs 15,000
Credit: Bank (Liability) - Rs 2,17,000
9. Goods and cash taken away by proprietor:
Debit: Proprietor's Drawings (Equity) - Rs 65,000
Credit: Goods (Asset) - Rs 25,000
Credit: Cash (Asset) - Rs 40,000
10. Goods sold to Charu:
Debit: Accounts Receivable - Charu (Asset) - Rs 1,20,000
Credit: Sales (Income) - Rs 1,20,000
Credit: Cost of Goods Sold (Expense) - Rs 80,000
Credit: Profit on Sales (Income) - Rs 40,000
11. Rent paid for the building:
Debit: Rent Expense (Expense) - Rs 60,000
Credit: Bank (Liability) - Rs 60,000
12. Goods sold to Sunil:
Debit: Accounts Receivable - Sunil (Asset) - Rs 24,000
Credit: Sales (Income) - Rs 24,000
Credit: Cost of Goods Sold (Expense) - Rs 20,000
Credit: Profit on Sales (Income) - Rs 4,000
13. Goods purchased from Nanda and supplied to Helen:
Debit: Purchases (Expense) - Rs 1,000
Debit: Accounts Payable - Nanda (Liability) - Rs 1,000
Credit: Accounts Receivable - Helen (Asset) - Rs 1,300
Credit: Sales (Income) - Rs 1,300
14. Goods received from Rohit and Sons and supplied to Madan:
Debit: Purchases (Expense) - Rs 2,700 (after 10% trade discount)
Credit: Accounts Payable - Rohit and Sons (Liability) - Rs 2,700
Debit: Accounts Receivable - Madan (Asset) - Rs 3,000
Credit: Sales (Income) - Rs 3,000
for such more question on journal entries
https://brainly.com/question/28390337
#SPJ8
How can I factor the following expression by grouping:
a) 4x^3 - 2x^2 + 8x - 4
Answers
The factored expression of 4x³ - 2x² + 8x - 4 is (2x² + 4)(2x - 1) by grouping
How to factor the expression by groupingFrom the question, we have the following parameters that can be used in our computation:
4x³ - 2x² + 8x - 4
Group the expression in 2's
So, we have
(4x³ - 2x²) + (8x - 4)
Factorize each group
2x²(2x - 1) + 4(2x - 1)
So, we have
(2x² + 4)(2x - 1)
Hence, the factored expression is (2x² + 4)(2x - 1)
Read more about expression at
https://brainly.com/question/31819389
#SPJ1
Jasmine drew a rectangle with an area of 4 square inches. Jasmine drew a new scaled version of the original rectangle using a scale factor of 5. What is the area, in square inches, of the new rectangle?
Answers
Answer:
the answer is 10 im pretty sure
Step-by-step explanation:
Find the indicated limit, if it exists. (2 points) limit of f of x as x approaches negative 1 where f of x equals 4 minus x when x is less than negative 1, 5 when x equals negative 1, and x plus 6 when x is greater than negative 1
Answers
Answer:
5
Step-by-step explanation:
The limit of f(x) at x=-1 is 5 when approached from the left or right. Since those limits are the same, the limit exists and is ...
\(\boxed{\lim\limits_{x\to-1}f(x)=5}\)

saif made 60 runs in 5 over and anus made 72 runs in 8 over whose performance was better
Answers
Saif's performance was better.
What is an expression?An expression contains one or more terms with addition, subtraction, multiplication, and division.
We always combine the like terms in an expression when we simplify.
We also keep all the like terms on one side of the expression if we are dealing with two sides of an expression.
Example:
1 + 3x + 4y = 7 is an expression.
3 + 4 is an expression.
2 x 4 + 6 x 7 – 9 is an expression.
33 + 77 – 88 is an expression.
We have,
We will compare the run rates of Saif and Anus.
The run rate is the average number of runs scored per over.
Now,
The run rate of Saif.
= 60 / 5
= 12 runs per over
And,
The run rate of Anus
= 72 / 8
= 9 runs per over
Therefore,
Saif's performance was better.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
What is the equation of the line through (2,3) and (-1,-12)
Answers
Answer:
slope intercept: y=5x-7
Step-by-step explanation:
first you need slope: y2-y1/x2-x1
-12-3/-1-2=
-15/-3=
5
then plug into this formula: y-y1=m(x-x1)
y-3=5(x-2)
y-3=5x-10
y=5x-7
Calculate the distance between the points and in the coordinate plane.

Answers
Step 1
State the formula for the distance between 2 points
\(D(EN)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)}\)where
\(\begin{gathered} x_2=-2 \\ x_1=3 \\ y_2=2 \\ y_1=-3 \end{gathered}\)Step 2
Find the distance between the points E and N
\(\begin{gathered} D(EN)=\sqrt[]{(-2-3)^2+(2-(-3))^2} \\ D(EN)=\sqrt[]{(-5)^2+(5)^2} \\ \end{gathered}\)\(\begin{gathered} D(EN)=\sqrt[]{25+25} \\ D(EN)=\sqrt[]{50} \\ D(EN)=7.071067812 \\ D(EN)\approx\text{ 7.07 to the nearest hundredth} \end{gathered}\)The distance between the points E and N approximately to the nearest hundredth= 7.07 units
the function has zeros at -1 and -11, and a minimum at -5
Answers
The minimum point on the graph is \((-6,25)\), which confirms that the function has a minimum at\(-6\).
What is graph?In mathematics, a graph is a diagram that shows the relationship between different sets of data. It is made up of points, which are also called vertices or nodes, that are connected by lines or curves called edges or arcs.
In mathematics, a function is a relation between two sets of data, such that each input in the first set corresponds to exactly one output in the second set. In other words, a function maps each input value to exactly one output value.
According to given information:
Let's start by writing the quadratic function in factored form, given that it has zeros at \(-1\) and \(-11\):
\(f(x) = a(x- (-1))(x- (-11))\)
Simplifying, we get:
\(f(x) = a(x+1)(x+11)\)
To find the value of a, we need to use the fact that the function has a minimum at \(-5\). Since the vertex of the parabola is at the minimum point, we know that the x-coordinate of the vertex is \(-5\). Therefore, we can use this information to find the value of a as follows:
\(-5 = (-1+(-11))/2\\-5 = -6\)
This tells us that the axis of symmetry of the parabola is \(x =-5\). Since we know that the function has zeros at \(-1\) and \(-11\), we can deduce that the vertex must lie halfway between these two zeros, at\(x = -6\). Therefore, the value of a is:
\(f(-6) = a((-6)+1)(-6) +11) = a(5) (-1) = -5a\)
We also know that the function has a minimum at this point, so we can use this to find the value of a:
\(f(-6) = -5\\-5= -5a\\\\a = 1\)
Therefore, the quadratic function that satisfies these conditions is:
\(f(x) = (x+1) (x+11)\)
We can check that this function has zeros at \(-1\) and \(-11\), and that it has a minimum at\(x =-6\) by finding its vertex:
x-coordinate of vertex = \((-1 +(-11))/2 =-6\)
y-coordinate of vertex =\(f(-6) = (-6+1)(-6+11) = 25\)
Therefore, the minimum point on the graph is \((-6,25)\), which confirms that the function has a minimum at -6.
Which of the following function has zeros at \(-1\) and\(-11\) and a minimum of \(-5\) ?
To know more about graph visit:
https://brainly.com/question/19040584
#SPJ1
A pail of water that holds 4 gallons (gal) needs to be filled with water from a swimming pool. How many times you will get a water from the pool using the a dipper that can hold 1 pint (pt) of water? (Use the conversion of 1 gal = 8 pt
Answers
Answer:
32 pints
Step-by-step explanation:
4 gallons * 8 pints/1 gallon = 32 pints
WILL GIVE BRAINLIEST + MAX POINTS!!!
Sara is working on a Geometry problem in her Algebra class. The problem requires Sara to use the two quadrilaterals below to answer a list of questions. Part A: For what one value of are the perimeters of the quadrilaterals the same? (Hint: The perimeter of a quadrilateral is the sum of its sides.) Part B: For what one value of are the areas of the quadrilaterals the same? (Hint: The area of a quadrilateral is the product of its base and height.) Please help me outtt!
Answers
HELLO
I NEEDED HELP WITH THE SAME QUESTION SO I PUT IT UP WITH A PIC SO U CAN ALSO GET AN ANSWER FROM THERE
HERE YA GO <3
https://brainly.com/question/24188218?referrer=searchResults
Answer:
heyy i did this problem a while ago and got kinda stuck on it

ill give brainly HURRY PLEASE

Answers
A hypothesis test was used to test the hypothesis that men drive faster on average than women. The p-value was 0.16 and the level of significance used was 0.1. Then there is sufficient evidence to conclude that, on average, men drive faster then women O false O true
Answers
On average, men drive faster then women
The statement is true.
What is p-value?
The p-value, used in null-hypothesis significance testing, represents the likelihood that the test findings will be at least as extreme as the result actually observed, assuming that the null hypothesis is true.
We are given a statement that,
A hypothesis test was used to test the hypothesis that men drive faster on average than women.
The p-value in that case was 0.16 and the level of significance used was 0.1
As the p value is greater than level of significance we can say that the null hypothesis is correct
Hence we can say that on average men drive faster than women
The statement is correct
To learn more about the hypothesis testing please refer the following link
https://brainly.com/question/15980493
#SPJ4
Can someone help me please

Answers
Answer:
7⅞
Step-by-step explanation:
NO.OF HATS TO BE MADE= 9
YARD OF YARN NEEDED TO MAKE EACH HAT= 7/8
THEN,
TOTAL YARDS OF YARN= 9*7/8
= 63/8
Given to write answer in mixed form= 7⅞
ThankYouPlease mark me as brainliest
Which is an infinite arithmetic sequence? a{10, 30, 90, 270, …} b{100, 200, 300, 400} c{150, 300, 450, 600, …} d{1, 2, 4, 8}
Answers
Answer:
C
Step-by-step explanation:
An arithmetic sequence has a common difference d between consecutive terms.
Sequence a
30 - 10 = 20
90 - 30 = 60
270 - 90 = 180
This sequence is not arithmetic
Sequence b
200 - 100 = 100
300 - 200 = 100
400 - 300 = 100
This sequence is arithmetic but is finite, that is last term is 400
Sequence c
300 - 150 = 150
450 - 300 = 150
600 - 450 = 150
This sequence is arithmetic and infinite, indicated by ........ within set
Sequence d
2 - 1 = 1
4 - 2 = 2
8 - 4 = 4
This sequence is not arithmetic
Thus the infinite arithmetic sequence is sequence c
find the quadratic polynomial, the sum of whose zeroes is 8 and their product is 12. hence, find the zeroes of the polynomial.
Answers
The required quadratic polynomial is \(x^{2} - 8x + 12 =0\) and roots of this quadratic polynomial are 2 and 6.
Let the roots of the quadratic equation be \(\alpha\) and \(\beta\) .
Given,
Sum of zeroes, \(\alpha +\beta = 8\)
Product of Zeroes, \(\alpha *\beta = 12\)
we know that,
Quadratic Equation can be written as :
\(x^{2} - (\alpha + \beta )x + \alpha \beta =0\)
Substituting the values in the above Equation,
\(x^{2} - (8)x + (12) =0\)
\(x^{2} - 8x + 12 =0\)
Hence, The required quadratic equation is \(x^{2} - 8x + 12 =0\) .
Now, let's factorize the equation to find its root:
\(x^{2} - 8x + 12 =0\)
\(x^{2} - 6x -2x+ 12 =0\)
\(x(x-6) -2(x-6)=0\)
\((x-6)(x-2)=0\)
⇒ \(x= 2,6\)
Therefore roots of the quadratic equation \(\alpha ,\beta\) are \(2,6\) .
Learn more about Quadratic Equation:
https://brainly.com/question/30098550
#SPJ4
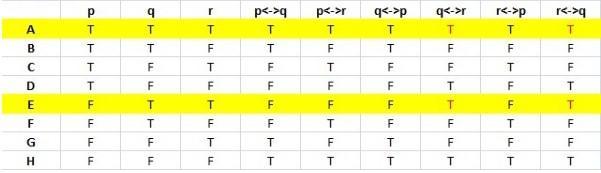
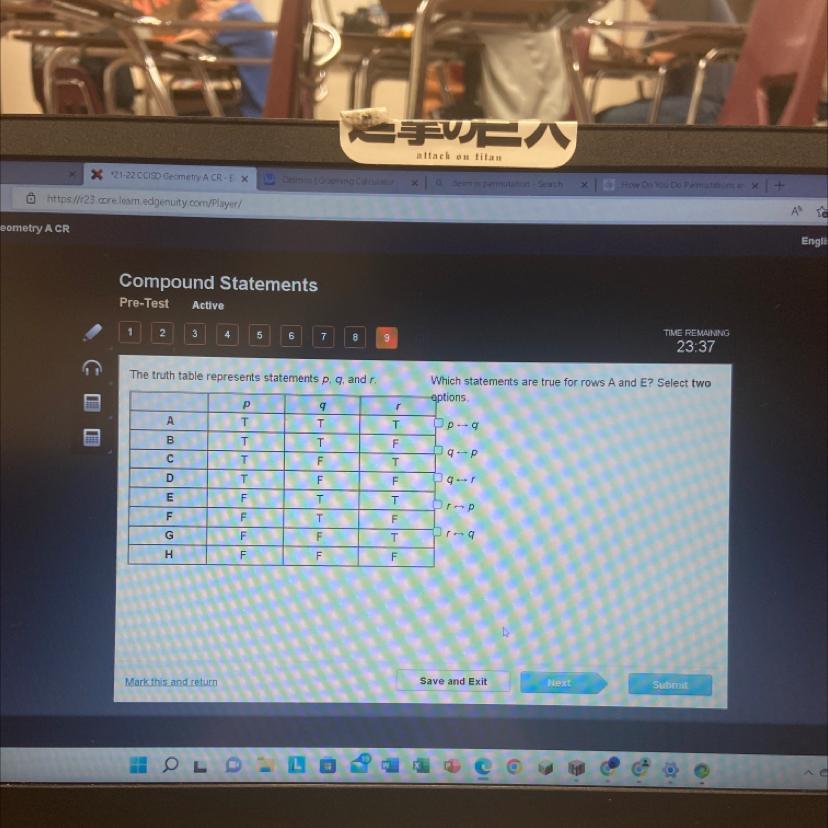
The truth table represents statements p, q, and r.
Р
9
r
A
T
T
B
T
F
C
T
T
F
F
T
F
F
F
T
F
F
DEFGH
Mark this and return
T
T
TE
F
T
T
F
F
Which statement is true for rows A, C, and E?
r- (p^q)
r- (pvq)
(q^r) → p
(avr)-p
Save and Exit
Next
Answers
The truth tables for the three variables p, q, and r have been provided to us as depicted below.
p q r
A T T T
B T T F
C T F T
D T F F
E F T T
F F T F
G F F T
H F F F
We must now determine which of the following propositions is true for rows A and E:
p ↔ q p ↔ r q ↔ p q ↔ r r ↔ p r ↔ q
In order to determine that, we must use the P -> Q table depicted in the image.
We are aware that only P <-> Q will be true if both propositions for P and Q are true. Therefore, using that approach, we can observe that the final answers are merely q <-> r and r <-> q.
Learn more about truth table here:
brainly.com/question/14458200
#SPJ9