Answers
Part a:
Let's express this as a fraction, where the rise is the numerator and the run is the denominator. The rise is 1 unit of height, and the run is 10 units of distance. Therefore, the gradient can be expressed as: 1/10
To find the angle that the road makes with the horizontal using trigonometry is: tan θ = 1/10
Solving for θ, we get:
θ = tan^(-1)(1/10) ≈ 5.7 degrees
Therefore, the road makes an angle of approximately 5.7 degrees with the horizontal.
Part b:
If the car drives 2 km along the road, we can use the angle calculated in part a to find the vertical height that the car has climbed. We know that the distance covered along the road is the run, which is 2 km or 2000 meters.
Using trigonometry again, we can find the vertical height climbed by the car, which is the opposite side. The tangent of the angle is: tan θ = 1/10
Let's rearrange this to solve for the opposite side, which is the vertical height climbed:
opposite side = adjacent side x tan θ
opposite side = 2000 x tan (5.7 degrees)
opposite side ≈ 200 meters
Therefore, the car has climbed approximately 200 meters vertically along the inclined road.
Related Questions
find two functions f and g
a. f(x) =
b. f(x) =

Answers
The functions f and g are:
a. f(x) = 1/x
b. g(x) = x + 2
a) To find two functions f and g such that (fog)(x) = 1/(x + 2), we need to determine how the composition of the two functions f and g produces the given expression.
Let's start by assuming g(x) = x + a, where a is a constant. This means that g(x) adds the constant a to the input x.
Next, let's determine the function f(x) such that (fog)(x) results in the desired expression. We have:
(fog)(x) = f(g(x)) = f(x + a)
b) To simplify the expression 1/(x + 2) and make it match f(g(x)), we can consider f(x) = 1/x.
Substituting the expressions for f(x) and g(x) into (fog)(x), we have:
(fog)(x) = f(g(x)) = f(x + a) = 1/(x + a)
Comparing this with the desired expression 1/(x + 2), we see that a = 2. Therefore, the functions f and g are:
a. f(x) = 1/x
b. g(x) = x + 2
Using these functions, we can verify the composition (fog)(x):
(fog)(x) = f(g(x)) = f(x + 2) = 1/(x + 2)
Thus, (fog)(x) = 1/(x + 2), which matches the desired expression.
For more such question on functions. visit :
https://brainly.com/question/11624077
#SPJ8
The question is in the image below

Answers
\(A \cup B = \{2,4,5,7,8, 9\}\)
Answer:
2,4,5,7,8,9 [final answer]
Step-by-step explanation:
Given that,
→ A = {2,4,5}
→ B = {5,7,8,9}
The union of two sets A and B is a set that contains all elements of A and B.
→ A∪B = {2,4,5,7,8,9}
The answer is 2,4,5,7,8,9.
A circle has radius 29.5 cm. What is the diameter?
Answers
Answer:
\(\huge\boxed{\sf D = 59 cm}\)
Step-by-step explanation:
Radius = 29.5 cm
We know that
Diameter = 2(Radius)
D = 2(29.5)
D = 59 cm
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807Can someone solve this Quadratic Equation using the formula (x=-b+and minus under the plus, then square root b^2-4ac divide in the bottom with 2a)
1. x^2=-5x+2
2.x^2+4x+17=8-2x

Answers
Step-by-step explanation:
We need to solve the given quadratic equations.
1.
\(x^2=-5x+2\\\\x^2+5x-2=0\)
Using the formula to find solutions.
We have, a = 1, b = 5 and c = -2
So,
\(x=\dfrac{-5\pm \sqrt{5^2-4(1)(-2)} }{2}\\\\x=0.37,-5.37\)
2.
\(x^2+4x+17=8-2x\\\\x^2+4x+17-8+2x=0\\\\x^2+6x+9=0\)
We have,
a = 1, b = 6 and c = 9
\(x=\dfrac{-6\pm \sqrt{6^2-4(1)(9)} }{2}\\\\x=-3,-3\)
Hence, this is the required solution.
A test was given to a group of students. The grades and gender are summarized below
A B C Total
Male 3 10 12 25
Female 14 2 13 29
Total 17 12 25 54
If one student is chosen at random from those who took the test,
Find the probability that the student got a 'A' GIVEN they are male.
Answers
The probability that the student got an 'A' given they are male is approximately 0.12 or 12%.
To find the probability that a student got an 'A' given they are male, we need to use Bayes' theorem:
P(A | Male) = P(Male | A) × P(A) / P(Male)
We can find the values of the terms in the formula using the information given in the table:
P(Male) = (25/54) = 0.46 (the proportion of all students who are male)
P(A) = (17/54) = 0.31 (the proportion of all students who got an 'A')
P(Male | A) = (3/17) = 0.18 (the proportion of all students who are male and got an 'A')
Therefore, plugging these values into the formula:
P(A | Male) = 0.18 × 0.31 / 0.46
P(A | Male) ≈ 0.12
So the probability that the student got an 'A' given they are male is approximately 0.12 or 12%.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
I just need to know the answer quick because I have to go somewhere
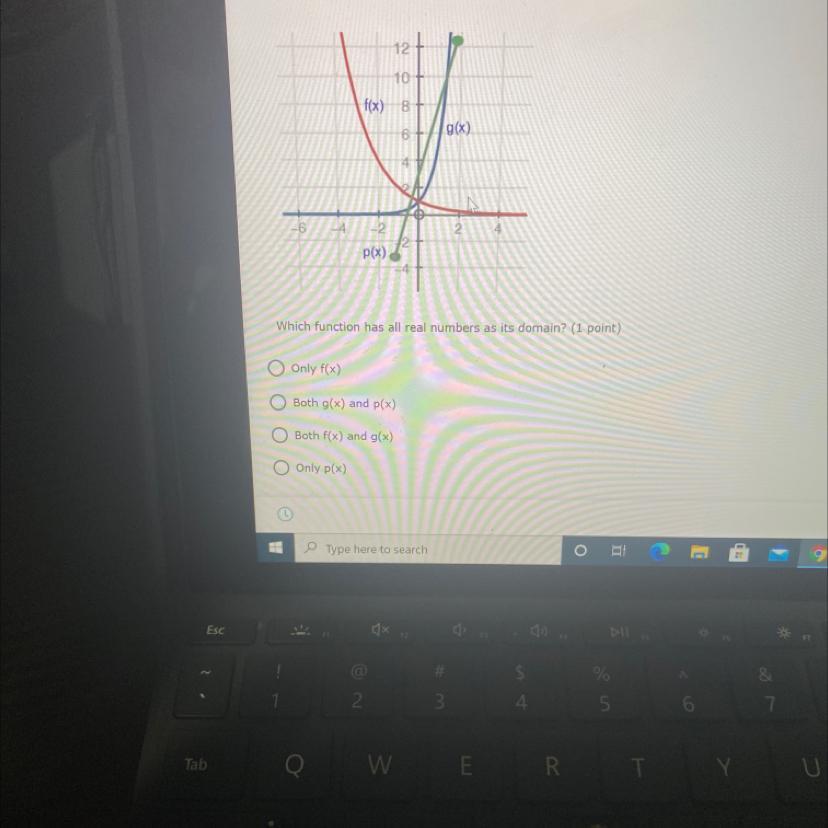
Answers
From the given graph, it is seen that f(x) is not defined for x<-4. The function g(x) is not defined for x>2
But the function p(x) represents a straight line which is defined for all real x.
Hence, the function p(x) has all real numbers as its domain.
Thus, the correct option is (D)
I need help with number 12

Answers
The solution is: equation of the parabola is:
y = 0.1(x + 5)² + 1.5
Equation of a parabola having vertex at (h, k) is given by,
y = a(x - h)² + k
From the given graph, vertex of the parabola is (-5, 1.5)
Therefore, equation of the parabola will be,
y = a(x + 5)² + 1.5
Since, this parabola passes through a point (0, 4)
4 = a(0 + 5)² + 1.5
4 = 25a + 1.5
25a = 2.5
a = 0.1
By substituting the value of 'a' in the equation of the parabola,
y = 0.1(x + 5)² + 1.5
learn more on parabola:
https://brainly.com/question/1615961
#SPJ1
complete question:
Write an equation of the parabola shown.
PLEASEEEE HURRY Which of the following constructions were never accomplished by the Greeks, with only a straight edge and compass
A trisecting any angle
B trisecting a line segment
C tripling a square
D doubling a cube
Answers
Therefore , the solution of the given problem of angles comes out to be Greeks failed to demonstrate that tripling a square with only a straight edge and compass was also unachievable.
An angle meaning is what?The highest and lowest walls of a skew are used to split the curved lines that make up its ends using Cartesian measurements. A collision between two poles at an intersection is a potential. Angle is another outcome of two things interacting. They resemble dihedral forms the most closely. A two-dimensional curve can be created by placing two line beams in various configurations between their ends.
Here,
The Greeks were unable to trisect a line section using only a straight edge and compass.
The Greeks proved that using only a straight edge and compass, it is impossible to trisect any angle or double a cube.
The Greeks failed to demonstrate that tripling a square with only a straight edge and compass was also unachievable.
To know more about angles visit:
https://brainly.com/question/14569348
#SPJ1
The perimeter of a rectangle is 12cm the area is 5cm square what is the length of the sides
Answers
Answer:
???
Step-by-step explanation:
Hope this helps

Given that 5 x : 9 = 8 : 3 Calculate the value of x . Give your answer in its simplest form.
Answers
In an certain species of newt, offspring are born either green or black. Suppose that 60% of these newts are born green. If we sample 133 of these newts at random, the probability distribution for the proportion of green newts in the sample can be modeled by the normal distibution pictured below. (Find the mean and two standard deviations away on each side)
Answers
The mean of the normal distribution is 0.6, and two standard deviations away on each side are:
Mean - 2 * Standard deviation = 0.6 - 2 * 0.051 = 0.498
Mean + 2 * Standard deviation = 0.6 + 2 * 0.051 = 0.702
What is probability distribution ?A probability distribution is a function that describes the likelihood of different outcomes or events in a particular scenario. It is often used in statistics and probability theory to analyze and model random phenomena. A probability distribution can be represented in various forms, including graphs, charts, and mathematical equations. The most common types of probability distributions are the normal distribution, binomial distribution, Poisson distribution, and exponential distribution.
According to given information :Given that the probability distribution for the proportion of green newts in the sample can be modeled by the normal distribution. We know that the normal distribution is characterized by its mean and standard deviation.
Since we have a large sample size of 133 newts, we can use the central limit theorem to approximate the distribution of the sample proportion of green newts to be normal with a mean of 0.6 (the population proportion) and a standard deviation of:
sqrt((0.6 * 0.4) / 133) = 0.051
Therefore, the mean of the normal distribution is 0.6, and two standard deviations away on each side are:
Mean - 2 * Standard deviation = 0.6 - 2 * 0.051 = 0.498
Mean + 2 * Standard deviation = 0.6 + 2 * 0.051 = 0.702
To know more about probability distribution visit :
https://brainly.com/question/23286309
#SPJ1
Find 10x+y when x= 10 and y = 3.
The answer is
Answers
Answer:
\(10x + y \\ 10(10) + 3 \\ 100 + 3 = 103\)
I hope I helped you^_^
which of the following is equivalent to x^2 -5x +6
Answers
Hello!
x² - 5x + 6
= (x² - 2x) + (-3x + 6)
= x(x - 2) - 3(x - 2)
= (x - 2)(x - 3)
What is (123
) ÷ (18
)?
Answers
Answer:
6.8333333333 or 41/6
Step-by-step explanation:
Please Help Really stuck

Answers
Answer:
4 2/3 mph
Step-by-step explanation:
A boat travels 15 miles upstream and 19 miles downstream.
If the boat travels 8 mph in still water, find the speed of the current if the total trip takes 6 hours.
Let c = the speed of the current
then
(8+c) = effective speed downstream
and
(8-c) = effective speed upstream
Write a time equation: time = dist/speed
Upstream time + downstream time = 6 hrs
\(\frac{15}{8-c} +\frac{19}{8+c}=6\)
120+15c+152-19c=384-6c²
6c²-4c-112=0
c=4 2/3
HELP! Please explain

Answers
Answer:
∠1 = 110
Step-by-step explanation:
Vertically Opposite angles, means that when you have two parrallel lines, The angles opposite of each other are equal. So 4 = 2 on the bottom line.
This means angle 1 is equal to it's opposite angle, 110'.
Answer:
110 degrees
Step-by-step explanation:
Since completing the known angle is 70 degrees, angle 1 must be 70 degrees. It is also adjacent to 110, which means it equals the same.
calculate the value of:
1+3+5+....+43
Answers
Answer 52
Represent 2x + 3y = 6 by a graph. Write the coordinates of the point where it meets: (a) x-axis
Answers
The point where the line 2x + 3y = 6 intersects the x-axis is (3, 0). This means that when x is equal to 3, y is equal to 0.
To graph the equation 2x + 3y = 6, we can rewrite it in the slope-intercept form, y = mx + b, where m represents the slope and b represents the y-intercept.
Starting with the given equation, we isolate y to one side:
3y = -2x + 6
y = (-2/3)x + 2
Now, we have the equation in slope-intercept form, y = (-2/3)x + 2. The slope is -2/3, and the y-intercept is (0, 2).
To find the point where the graph intersects the x-axis, we need to determine the coordinates where y is equal to zero. This occurs when the line crosses the x-axis.
Setting y = 0 in the equation, we have:
0 = (-2/3)x + 2
(-2/3)x = -2
x = (-2)(-3/2) = 3
Therefore, the point where the line 2x + 3y = 6 intersects the x-axis is (3, 0). This means that when x is equal to 3, y is equal to 0, indicating the point of intersection with the x-axis on the graph.
To more on Graph:
https://brainly.com/question/19040584
#SPJ8
Drag each number to a box to complete the table. Each number may be used once or not at all
Answers
Each number should be dragged to a box to complete the table as follows;
Kilometers Meters
1 1,000
2 2,000
3 3,000
5 5,000
8 8,000
What is a conversion factor?In Science and Mathematics, a conversion factor can be defined as a number that is used to convert a number in one set of units to another, either by dividing or multiplying.
Generally speaking, there are one (1) kilometer in one thousand (1,000) meters. This ultimately implies that, a proportion or ratio for the conversion of kilometer to meters would be written as follows;
Conversion:
1 kilometer = 1,000 meters
2 kilometer = 2,000 meters
3 kilometer = 3,000 meters
4 kilometer = 4,000 meters
5 kilometer = 5,000 meters
6 kilometer = 6,000 meters
7 kilometer = 7,000 meters
8 kilometer = 8,000 meters
Read more on conversion factor here: brainly.com/question/28308386
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

45 POINTS PLEASE BE FAST 18-22 !! <33 (sorry if its blurry)

Answers
Answer:
18. Aileen
19. Edward
20. 25 seconds
21. 40 seconds
22. 55 seconds or 3 minutes, 20 seconds - 4 minutes, 15 seconds
Step-by-step explanation:
Hello! Alright, let's start breaking down the answers one by one!
18.
To begin with 18, we just have to simply compare everyone's time to the actual time! (3 minutes and 46 seconds). To make this easier for us, we should convert everyone's time into the form of minutes/seconds. So it would be:
Aileen: 3 minutes, 50 secondsAlejandra: 4 minutesChris: 3 minutes, 20 secondsDavina: 3 minutes, 40 secondsEdward: 4 minutes, 15 secondsAs you can compare here, the closest person here would be Aileen being 4 seconds off from the actual time.
19.
Based off of what we did in 18, we can use that chart to compare, we just have to find the time differences to see who is more off from the actual time and that would be:
Aileen: +4 secondsAlejandra: +14 secondsChris: -26 secondsDavina: -6 secondsEdward: +29 secondsHere in this case, Edward's estimate would be the farthest away with +29 seconds.
20.
To calculate the time difference between these two, we simply just take the data from 18 and compare Aileen and Edward. In this case, it would be a difference of 25 seconds.
21.
Again, we take a look at Alejandra and Chris's estimate and compare the time difference. In this case, it would be 40 seconds.
22.
Finally, to figure out the range, we essentially just need to figure out the time difference between the lowest time and the highest time estimated. So that would be Chris's time (3 minutes, 20 seconds) and Edward's time (4 minutes, 15 seconds) and that would be 55 seconds.
In the diagram below of circle O, chords AD and BC intersect at E, and chords AB and CD are drawn.
Which statement must always be true?
PLEASE HELP!

Answers
The correct answer is (C) \(\angle B \cong \angle C.\) when In the diagram below of circle O, chords AD and BC intersect at E.
What is a circle ?
A circle is a two-dimensional geometric shape that consists of all the points in a plane that are at a fixed distance from a given point, called the center.
In the given diagram, we have a circle O with chords AB, CD, AD, and BC. The chords AD and BC intersect at point E.
Based on the diagram, we can see that the opposite angles in the quadrilateral AEDC are supplementary (i.e., they add up to 180 degrees). Therefore, we have:
\(\angle A + \angle C = 180^\circ\)
Similarly, the opposite angles in the quadrilateral BEFC are supplementary. Thus,
\(\angle B + \angle C = 180^\circ\)
We can rewrite the second equation as:
\(\angle C = 180^\circ - \angle B\)
Substituting this value of \angle C into the first equation, we get:
\(\angle A + 180^\circ - \angle B = 180^\circ\)
Simplifying, we get:
\(\angle A = \angle B\)
Therefore, the correct answer is (C) \(\angle B \cong \angle C.\)
To learn more about chords visit the link :
https://brainly.com/question/1654080
#SPJ1
Choose the equation that represents the solutions of 0 = 0.25x² - 8x. 0.25± √(0.25)² - (4)(1)(-8) 2(1) O O X = X = X = X = -0.25± √√(0.25)² – (4)(1)(-8) 2(1) 8± √(-8)²-(4)(0.25) (0) 2(0.25) -8± √(-8)²-(4)(0.25)(0) 2(0.25)
Answers
The given equations represent the solutions of 0 = 0.25x² - 8x
What is an equation?An equation is a mathematical statement that shows the equality of two expressions, typically separated by an equal sign. Equations are used to solve problems and model real-world situations in many fields, including physics, engineering, and finance.
Redirecting to answer:
The equation 0 = 0.25x² - 8x can be rewritten as:
0.25x² - 8x = 0
Factoring out x gives:
x(0.25x - 8) = 0
So the solutions are x = 0 and 0.25x - 8 = 0, which gives x = 32.
Therefore, none of the given equations represent the solutions of 0 = 0.25x² - 8x
To know more about equation:
brainly.com/question/29657983
#SPJ1
a water snake in a well is 30 M below the ground level its lights 20 m upward and then slips down 10 M how far it is from the ground level
\( - 30 - + 20 - - 10\)
Answers
If the water snake is initially 30 meters below the ground level and then climbs 20 meters upward, it will be 30 - 20 = 10 meters below the ground level. However, if it then slips down 10 meters, it will be 10 + 10 = 20 meters below the ground level.
A lighthouse is located on a small island 5 km away from the nearest point P on a straight shoreline and its light makes six revolutions per minute. How fast is the beam of light moving along the shoreline when it is 1 km from P? (Round your answer to one decimal place.)
Answers
Answer:
The beam of light is moving along the shoreline at a velocity of approximately 196 kilometers per second.
Step-by-step explanation:
The statement is described geometrically in the image attached below by means of a right triangle. All variables are described below:
\(OP\) - Minimum distance between lighthouse and the straight shoreline, in kilometers.
\(PP'\) - Distance along the straight shoreline, in kilometers.
\(\theta\) - Angle of rotation of the lighthouse, in sexagesimal degrees.
To find the rate of change of distance along the straight shoreline (\(\frac{dPP'}{dt}\)), in kilometers per minute, we use the following trigonometric relationship:
\(PP' = OP \cdot \tan \theta\) (1)
Then, we differentiate this expression in time:
\(\frac{dPP'}{dt} = OP\cdot \dot \theta \cdot \sec^{2}\theta\) (2)
Where \(\dot \theta\) is the rate of change of the angle of rotation of the lighthouse, in radians per minute.
The angle at the given instant is calculated by (1): \(OP = 5\,km\), \(PP' = 1\,km\)
\(\theta = \tan^{-1} \left(\frac{PP'}{OP} \right)\)
\(\theta \approx 11.310^{\circ}\)
If we know that \(\dot \theta = 37.699\,\frac{rad}{min}\), \(\theta \approx 11.310^{\circ}\) and \(OP = 5\,km\), then the rate of change is:
\(\frac{dPP'}{dt} \approx 196,035\,\frac{km}{min}\)
The beam of light is moving along the shoreline at a velocity of approximately 196 kilometers per second.

Cassie has a total of 110 coins in her piggy bank. All the coins are quarters and dimes. The coins have a total value of $20.30. How many quarters and how many dimes are in the piggy bank?
Answers
Answer:
48 dimes and 62 quarters
Step-by-step explanation:
Last week, Maria bought k pounds of cherries at the regular price of $2.75 per pound. This week, cherries were on sale for 20 percent off, and maria bought twice as many pounds as she bought last week, which of the following is the total in dollar, Maria paid for the cherries last week and this week
Answers
Answer:
$7.15k
Step-by-step explanation:
So the first week, she used $2.75k
Then, you can calculate the amount for one pound the next week by doing 0.8 * 2.75 = 2.2
So the second week she used 2 * 2.2 * k = $4.4k
$4.4k + $2.75k = $7.15k
Might be wrong so check it.
pls answer me thus question

Answers
Answer:
iii is the correct answer (the third one)
Step-by-step explanation:
additive inverse is the same as the reciprocal
It is when the denominator and numerator are swapped around
So the inverse of 3/9 is 9/3
Brainliest would be appreciated
At a certain conference the information technology session and the social media session occur at the same time so it is impossible for an attendee to sit in on both sessions. If the probability that an attendee sits in on the information technology session is 0.11, and the probability that an attendee sits in on the social media session is 0.62, what is the probability that an attendee sits in on the information technology session or the social media session?
Answers
Answer:
0.73 = 73% probability that an attendee sits in on the information technology session or the social media session.
Step-by-step explanation:
What is the probability that an attendee sits in on the information technology session or the social media session?
They cant be in both sections simultaneously, so this probability is the sum of each probability.
0.11 = 11% probability that an attendee sits in on the information technology session
0.62 = 62% probability that an attendee sits in on the social media session
0.11 + 0.62 = 0.73
0.73 = 73% probability that an attendee sits in on the information technology session or the social media session.
Is 0.03<0.1 correct?
Answers
Answer:
yes
Step-by-step explanation:
This is correct because 0.1 or 0.10 is greater than 0.03
Find the numbers whose sum is 9, if
three times the first number increased
by two times the second number
equals 22.
Answers
Therefore , the solution of the given problem of linear equation comes out to be the numbers are -2 and 14.
A linear equation definition.The equation y=mx+b is the basis of a linear regression model. The y-intercept is m, and the slope is B. Although y and x are different elements, the previous sentence is frequently alluded to as a "maths problem with two variables. In bivariate linear equations, there are only two variables. The solutions of the application domains of linear equations are always zero.
Here,
Let x and y be the first and second numbers, respectively. The information provided lets us know that:
=> 3x + 2y = 22
Additionally, we are aware that the two numbers add up to 9, therefore
=> x + y = 9
We can employ a strategy like substitution to discover the values for x and y. One equation with one variable can be solved, and the solution can then be used as an expression in the other equation.
The first equation for y can be solved as follows:
=> y = (22 - 3x)/2
After that, change y in the second equation to the following expression:
=> x + (22 - 3x)/2 = 9
When we simplify and find x, we obtain:
=> 2x + 22 = 18
=> x = -2
Knowing that x = -2, we may re-apply it to the initial equation to determine the y :
=> y =28/2 =14.
To know more about linear equation visit:
https://brainly.com/question/11897796
#SPJ1
