PLEASE HELP ME
i need to bring my grade up so it would mean a lot if you helped out and answered
(please don't put something random for the points)
(if you don't know PLEASE dont answer)
20 points :)

Answers
Answer:
D
Step-by-step explanation:
25/100 simplifies to 1/4
Answer:
1/4
Step-by-step explanation:
Turning 0.25 into a fraction:
0.25 = 25/100
Simplify:
25/100 = 1/4
1/4 is your answer
Hope this helps!
Related Questions
17.
Peter transports metal bars in his van.
The van has a safety notice: "Maximum Load 1200 kg".
Each metal bar has a label: "Weight 60 kg".
For safety reasons, Peter assumes that:
1200 is rounded correct to 2 significant figures, and
60 is rounded correct to 1 significant figure.
Calculate the greatest number of bars that Peter can safely put into the van if his assumptions are
correct.
Answers
Answer:
17 bars
Step-by-step explanation:
Peter wants to compute the maximum number of bars he can load safely if the load limit of 1200 kg and the bar weight of 60 kg are each rounded to the number of significant digits those numbers have.
Range of valuesThe error in a rounded number is assumed to be as much as half of the least significant digit of the number.
Peter's load limit may actually be as low as ...
1200 kg - (1/2)(100 kg) = 1150 kg . . . . . . . 1200 is rounded to nearest 100
Peter's bar weight might be as high as ...
60 kg + (1/2)(10 kg) = 65 kg . . . . . . . . . . . 60 is rounded to nearest 10
Safe loadingIf Peter has maximum-weight bars and does not want to exceed the minimum his load limit might be, the number of bars he can load is ...
(1150 kg) / (65 kg/bar) ≈ 17.7 bars
The greatest number of bars Peter can load safely is 17.
Two different students decide to compare their businesses. Scooter makes his own t-shirts,
while Karissa does computer repairs. For both models, x represents the number of sales made
each month and f(x) represents total money for each individual. The two functions below model
their respective businesses:
Scooter: f(x) = 200 + 15x
Karissa: f(x) = 80 + 35x
a. Describe what the slope and y intercept represent for both models based on the context.
Compare the two functions. What is one statement you could say about each?
b.
C.
In one month, Scooter sells 20 shirts. That same month, Karissa does 12 repairs. Who had
the better month?
Answers
a) Comparing the two functions, Scooter's business has a lower slope of 15 compared to Karissa's business with a slope of 35. b) Both Scooter and Karissa earned a total of $500 in that month. Therefore, they had an equal month in terms of total money earned.
How to Describe what the slope and y intercept represent for both models based on the contexta) In the context of Scooter's business, the slope of the function f(x) = 200 + 15x represents the rate at which the total money earned increases with each additional sale. Each unit increase in x (number of sales) results in an increase of $15 in total money earned. The y-intercept of 200 represents the initial amount of money Scooter already had before making any sales.
In the context of Karissa's business, the slope of the function f(x) = 80 + 35x represents the rate at which the total money earned increases with each additional repair job. Each unit increase in x (number of repairs) results in an increase of $35 in total money earned. The y-intercept of 80 represents the initial amount of money Karissa already had before doing any repair jobs.
Comparing the two functions, Scooter's business has a lower slope of 15 compared to Karissa's business with a slope of 35. This means that Karissa's business earns more money per repair job compared to Scooter's business per t-shirt sale.
b) To determine who had the better month, we need to calculate the total money earned by each individual based on the given sales/repairs.
For Scooter, with x = 20 (number of shirts sold):
f(x) = 200 + 15x
f(20) = 200 + 15 * 20
f(20) = 200 + 300
f(20) = 500
For Karissa, with x = 12 (number of repairs):
f(x) = 80 + 35x
f(12) = 80 + 35 * 12
f(12) = 80 + 420
f(12) = 500
Both Scooter and Karissa earned a total of $500 in that month. Therefore, they had an equal month in terms of total money earned.
learn more about functions at https://brainly.com/question/11624077
#SPJ1
Please give me the correct answer.

Answers
Step-by-step explanation:
4n = - 6
n = - 6/4
n = - 3/2
And that it
Answer:
n = 1.5
Step-by-step explanation:
So, you left off on where we subtracted 40 from both sides.
34 - 40 = -6
4n = -6
Now, divide both sides by 4 to ultimately isolate the variable:
4n/4 = -6/4
Therefore your answer is -1.5
Please answer this correctly

Answers
The right answer is 40 cm
please see the attached picture for full solution
Hope it helps
Good luck on your assignment

HELP PLEASE I’m having troubles!!!
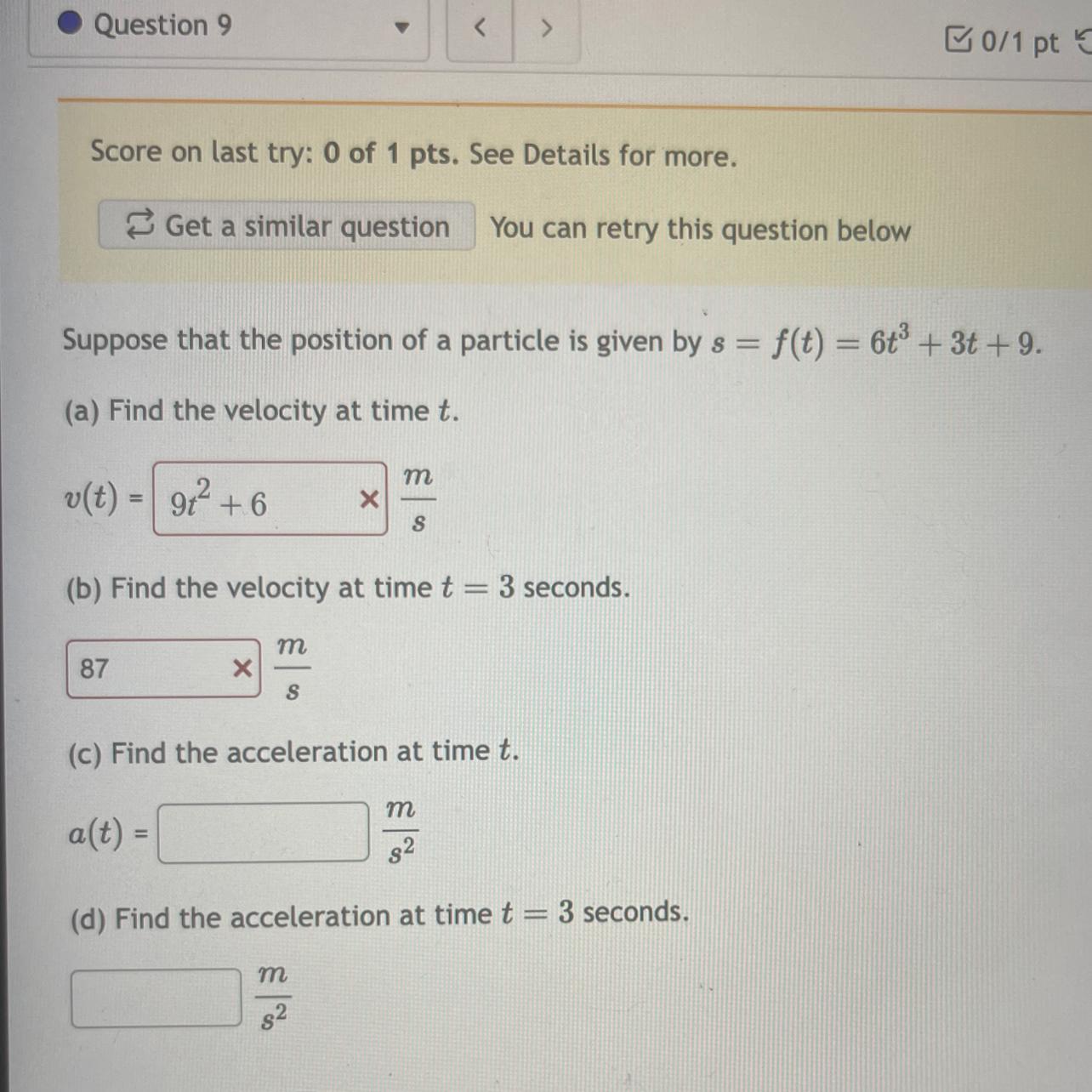
Answers
1. The velocity at time t , v(t) = (18t² + 3 ) m/s
2. The velocity at time t = 3 seconds = 165 m/s
3. The acceleration at time t, a(t) =( 36t )m/s²
4. The acceleration at time t = 3 seconds = 108 m/s²
What is instateanou velocity and acceleration?The quantity that tells us how fast an object is moving anywhere along its path is the instantaneous velocity.
Instantaneous acceleration is defined as the ratio of change in velocity during a given time interval such that the time interval goes to zero.
1. s(t) = 6t³ + 3t +9
to find the velocity at time t, we differentiate s(t)
= 18t² + 3
2. at t = 3s
= 18(3)² +3
= 165 m/s²
3. v(t) = 18t² + 3
to get the acceleration at time t, we differentiate v(t)
= 36t
4. when t = 3
a = 36 × 3
= 108 m/s²
learn more about instantaneous velocity and acceleration from
https://brainly.com/question/2234298
#SPJ1
A direct variation includes the points (2,18) and (n,9). Find n?
Answers
The value of the n is 1
In a direct variation, the relationship between two variables is of the form y = kx, where k is a constant of proportionality.
To find the constant of proportionality k in this problem, we can use the fact that the given points satisfy the equation for direct variation.
(2,18) is one of the given points, so we can substitute these values into the equation y = kx and solve for k:
18 = k(2)
k = 18/2
k = 9
Now that we have found the value of k, we can use it to find n when y = 9:
9 = 9n
n = 1
Therefore, the value of n is 1.
Learn more about coordinates here:
https://brainly.com/question/20282507
#SPJ1
If y is 9, what is x?
Answers
Answer:
Ima just steal the points
Step-by-step explanation:
Scott invested a total of $5400 at two separate banks. One bank pays simple interest of 10% per year while the other pays simple interest at a rate of 8% per year. If Scott eamed $492.00 in interest during asingle year, how much did he have on deposit in each bank?
Answers
Given:
Total principal = $5400
Interest rate of bank A = 10% = 0.10
Interest rate of bank B = 8% = 0.08
Total interest = $492
Let's find how much he deposited in each bank.
Equation for total principal:
A + B = 5400
Equation for total interest:
0.10A + 0.08B = 492
Hence, we have the system of equations:
A + B = 5400
0.10A + 0.08B = 492
Where A and B represents the amount deposited in each bank.
Let's solve the system simultaneously using substitution method:.
Rewrite the first equation for A:
A = 5400 - B
Substitute (5400 - B) for A in equation 2:
\(\begin{gathered} 0.10(5400-B)+0.08B=492 \\ \\ 540-0.1B+0.08B=492 \\ \\ -0.1B+0.08B=492-540 \\ \\ -0.02B=-48 \end{gathered}\)Divide both sides by -0.02:
\(\begin{gathered} \frac{-0.02B}{-0.02}=\frac{-48}{-0.02} \\ \\ B=2400 \end{gathered}\)Now, substitute 2400 for B in either of the equations:
\(\begin{gathered} A=5400-B \\ \\ A=5400-2400 \\ \\ A=3000 \end{gathered}\)Therefore, we have the following:
Amount deposited in the bank that pays 10% interest = $3000
Amount deposited in the bank that pays 8% interest = $2400
• ANSWER:
Amount deposited in the bank that pays 10% interest = $3000
Amount deposited in the bank that pays 8% interest = $2400
40=3x+x^2
How do I find the answer to this
Answers
Answer:
x = -8, x = 5
Step-by-step explanation:
This can be solved using Factorization method:
\( 40 = 3x + {x}^{2} \\ \\ \implies \: {x}^{2} + 3x - 40 = 0 \\ \\ \implies \: {x}^{2} + 8x - 5x- 40 = 0 \\ \\ \implies \: x({x} + 8) - 5(x + 8) = 0 \\ \\ \implies \: ({x} + 8) (x - 5) = 0 \\ \\ \implies \: ({x} + 8) = 0 \: \: or \: \: (x - 5) = 0 \\ \\ \implies \: x = - 8 \: \: or \: \: x = 5 \\ \\ x = - 8, \: \: 5\)
Please help!
Whoever answers right gets brainliest!!!!

Answers
Answer:
\(y - 4 = - 3(x - 2)\)
The table shows a function.
ху
2 20
3 10
40
Part A: Is the function linear or nonlinear?
Part B: How did you determine if the function was linear or nonlinear?
Answers
Part A: The function is nonlinear.
Part B: We determined the function to be nonlinear because the corresponding y-values do not change by a constant rate as the x-values increase, indicating a lack of a linear relationship.
Part A: The given function is nonlinear.
Part B: To determine whether the function is linear or nonlinear, we need to examine the relationship between the x-values and the corresponding y-values in the table.
In a linear function, there is a constant rate of change between the x and y values.
This means that for every increase in x by a fixed amount, the corresponding y value will change by a constant amount.
If we look at the x-values in the given table (2, 3, 4), we can see that they are increasing by a fixed amount of 1 each time.
However, when we examine the corresponding y-values (20, 10, 40), we don't see a constant rate of change.
The y-values are not changing by the same amount for each increase in x.
For instance, when x increases from 2 to 3, the y-value decreases from 20 to 10.
This indicates a non-linear relationship as the change in y is not constant for each unit increase in x.
Additionally, when x increases from 3 to 4, the y-value jumps significantly from 10 to 40, which further confirms the nonlinear nature of the function.
Based on these observations, we can conclude that the given function is nonlinear.
For similar question on nonlinear.
https://brainly.com/question/2030026
#SPJ8
Evaluate (–1)8 + (–1)7 – 16 – 14 – (–1)2. Pay attention to the placement of the parentheses and negative signs. Question 1 options: A) 5 B) –3 C) –4 D) –23
Answers
Original Expression: (-1)8+(-1)7-16-14-(-1)2.
Evaluating: -8-7-16-14+2
-8-7=-15-16=-31-14=-45+2=-43.
The answer is -43 according to PEMDAS.
Suppose that the lifetimes of a certain kind of light bulb are normally distributed with a standard deviation of 110 hours. If exactly 90% of the bulbs die before 930 hours, find the mean lifetime of the bulbs. Carry your intermediate computations to at least four decimal places.
Answers
Answer:
sorry bro
Step-by-step explanation:
i really need the points
classify the following differential equation s given in both standard and differential form. Q5 only

Answers
y' = 2xy + x
Rewriting it in differential form, we get:
(2xy + x)dx - dy = 0
This is a first-order linear differential equation, which can be written in the form:
y' + P(x)y = Q(x)
where P(x) = -2x and Q(x) = x.
Therefore, the differential equation is a first-order linear differential equation.
A stained-glass window is shaped like a right triangle. The hypotenuse is 15feet. The length of one leg is three more than the other. Find the lengths of the legs.
Answers
let us build equation for unknown legs
If we keep the length pf one leg as x
the other leg would be x +3
so we can build a relationship using pythagoras theorem
x^2 + (x+3)^2 = 15^2
x^2 + x^2 + 6x + 9 = 225
2x^2 + 6x + 9 = 225
2x^2 + 6x+ 9-225 = 0
2x^2 + 6x - 216 = 0
x^2 + 3x - 108 = 0 dividing whole equation by 2
x^2 + 12x - 9x - 108 = 0
x ( x + 12 ) - 9 (x + 12) = 0
(x -9) ( x +12) = 0
solutions for x are
x = 9 or x = -12
as lengths cannot be negative
one side length is 9cm
and other which is( x + 3)
9 + 3
12cm
The lengths of the legs of the right angled triangle is 9 feet and 12 feet.
Pythagoras theorem is used to show the relationship between the sides of a right angled triangle. It is given by:
Hypotenuse² = First Leg² + Second leg²
Let x represent the length of one leg. The other leg is three more = x + 3, hypotenuse = 15 ft. Hence:
15² = x² + (x + 3)²
x² + 6x + 9 + x² = 225
2x² + 6x - 216 = 0
x² + 3x - 108 = 0
x = - 12 or x = 9
Since the length cant the negative hence x= 9, x + 3 = 12
The lengths of the legs of the right angled triangle is 9 feet and 12 feet.
Find out more at: https://brainly.com/question/10040532
PLEASE HELP!!! 20 POINTS AND WILL MARK BRAINLIEST
[A] state which becomes progressively more and more a unity will cease to be a state at all. Plurality of numbers is natural in a state; and the further it moves away from plurality towards unity, the less of a state it becomes.
Aristotle believed that the citizens of a successful state must
share the same beliefs.
follow the leadership of a dictator.
hold annual elections.
allow for a diversity of opinions.
Answers
Answer:
allow for a diversity of opinions
Step-by-step explanation:
Graph the line whose y-intercept is -1 and whose x- intercept is 1
Answers
Solution
- The formula for finding the equation of a line given its x and y-intercepts is:
\(\begin{gathered} -\frac{y_c}{x_c}=\frac{y-0}{x-x_c}=\frac{y-y_c}{x} \\ \\ where, \\ (0,y_c)\text{ is the y-intercept} \\ (x_c,0)\text{ is the x-intercept} \end{gathered}\)- Thus, we can solve the question as follows:
\(\begin{gathered} -\frac{-1}{1}=\frac{y-0}{x-1} \\ \\ 1=\frac{y}{x-1} \\ \\ \therefore y=x-1 \end{gathered}\)Final Answer
The equation of the line is
\(y=x-1\)- The graph of the equation is given below:

To rationalize a denominator that has more than one term, you multiply the
fraction by B+ B, where B is the conjugate of the denominator.

Answers
Answer:
False.
Explanation:
To rationalize a denominator that has more than one term, you multiply the fraction by \(\frac{b}{b}\), where "b" is the conjugate of the denominator not the numerator.
false
you multiply both the denominator and the numerator not just the fraction.
What is an equation of the line that passes through the point (-8,0) and is perpendicular to the line x+2y=14
Answers
Step-by-step explanation:
let eqn be y = mx + b.
Since perpendicular, m = - 1/(-0.5) = 2
sub (-8, 0):
0 = 2(8) + b
b = - 16
therefore equation is y = 2x - 16
Topic: coordinate geometry
If you like to venture further, feel free to check out my insta (learntionary). I'll be constantly posting math tips and notes! Thanks!
you can make one of the following investments:
Option 1: $50 initial investment with an average annual growth rate of 9% starting at age 30
Option 2: $50 initial investment with an average annual growth rate of 8% starting at age 20
Option 3: $100 initial investment with an average annual growth rate of 7% starting at age 25

Answers
Based on these calculations, Option 3 yields the highest future value at age 35.
How to solveTo compare the investment options at different ages, we can use the future value formula:
FV = PV * (1 + r)^t
where:
FV = future value of the investment
PV = present value or initial investment
r = annual growth rate (as a decimal)
t = number of years the investment grows
Here are the general equations for each option:
Option 1: FV1 = 50 * (1 + 0.09)^(t - 10)Option 2: FV2 = 50 * (1 + 0.08)^tOption 3: FV3 = 100 * (1 + 0.07)^(t - 5)To compare the options at ages 20, 25, 30, and 35, calculate the future value for each option at those ages by plugging in the corresponding value of t.
Age 20:
FV1 = N/A (Option 1 hasn't started yet)
FV2 = 50 * (1 + 0.08)^0 = $50
FV3 = N/A (Option 3 hasn't started yet)
Age 25:
FV1 = N/A (Option 1 hasn't started yet)
FV2 = 50 * (1 + 0.08)^5 ≈ $73.86
FV3 = 100 * (1 + 0.07)^0 = $100
Age 30:
FV1 = 50 * (1 + 0.09)^0 = $50
FV2 = 50 * (1 + 0.08)^10 ≈ $107.95
FV3 = 100 * (1 + 0.07)^5 ≈ $140.26
Age 35:
FV1 = 50 * (1 + 0.09)^5 ≈ $77.16
FV2 = 50 * (1 + 0.08)^15 ≈ $157.46
FV3 = 100 * (1 + 0.07)^10 ≈ $196.72
Based on these calculations, Option 3 yields the highest future value at age 35.
Read more about investment here:
https://brainly.com/question/27717275
#SPJ1
my father bought a robot for 670 2.50 and a toy car for 300 19.25 how much change did he get for his 1000.00
A.7.25 B.15.75cm C.27.75cm D.10.25
Answers
Answer:
Step-by-step explanation:
If it is supposed to be 672.50 and 319.25 then you can just go 1000 minus 672.50 which is 327.50 and then subtract 319.25 to get 8.25. But your answers show cm and none show the right answer. So, if it's rounding then choose A.
Use las propiedades de numeros reales para escribir la expresion sin parentesis
3(x+y)
4(2m)
-5/2(2x-4y)
Answers
Answer:
3x+3y
8m-5x
-5x+10y
Step-by-step explanation:
Algebra 1
Find the x and y intercepts for the following equation. 4x - 2y = 16
Answers
Answer:
( 4, 0 ) and ( 0,-8 )
Step-by-step explanation:
→ Rearrange into y = mx + c format
4x - 2y = 16
→ Minus 4x from both sides
-2y = -4x + 16
→ Divide everything by 2
-y = -2x + 8
→ Multiply everything by -1
y = 2x - 8
→ Substitute x = 0 to find the y-intercept and y = 0 to find the x intercept
x = 0 then y = -8 so ( 0,-8 )
y = 0 then x = 4 so ( 4, 0 )
Find the length of the third side. If necessary, round to the nearest tenth.
4.
2

Answers
Formula:
C^2 =a^2 + b^2
Answer = 4.47
Nearest tenth= 4.5

The length of the third side of the triangle is 4.5 units.
What is Pythagoras Theorem?
The Pythagorean theorem, or Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle.
Here, sides of triangle is AB = 4 , BC = 2
By Pythagoras Theorem,
AC² = AB² + BC²
AC² = 4² + 2²
AC² = 20
AC = √20
AC = 4.47
AC = 4.5
Thus, the length of the third side of the triangle is 4.5 units.
Learn more about Pythagoras Theorem from:
https://brainly.com/question/343682
#SPJ2
Angles E and F are vertical angles. If angle E has a measure of (4x+2)∘, and angle F has a measure of 70∘, what is the value of x?
Answers
Answer:
x=17
Step-by-step explanation:
since vertical angles are equal to each other and E=F
(4x+2)=70⁰
4x=70-2
4x=68
4x*¼=68*¼
which give us x=17
Given f(x) = 3x² + 9x - 16, find f(-8)
Answers
Answer:
To find f(-8), we need to substitute -8 for x in the expression for f(x) and evaluate:
f(-8) = 3(-8)² + 9(-8) - 16
Simplifying this expression, we get:
f(-8) = 3(64) - 72 - 16
f(-8) = 192 - 72 - 16
f(-8) = 104
Therefore, f(-8) = 104 when f(x) = 3x² + 9x - 16.
Learn more about Graphing Functions here:
https://brainly.com/question/23945486
#SPJ5
In ΔQRS, s = 2.3 inches, ∠S=51° and ∠Q=44°. Find the area of ΔQRS, to the nearest 10th of an square inch.
Answers
Answer:
Area of ΔQRS = 2.3 square inches
Step-by-step explanation:
From the given information,
<S + <Q + <R = \(180^{o}\)
51 + 44 + <R = \(180^{o}\)
95 + <R = \(180^{o}\)
<R = \(180^{o}\) - 95
= \(85^{o}\)
<R = \(85^{o}\)
Applying the Sine rule, we have;
\(\frac{q}{SinQ}\) = \(\frac{r}{SinR}\) = \(\frac{s}{SinS}\)
Using \(\frac{r}{SinR}\) = \(\frac{s}{SinS}\)
\(\frac{r}{Sin 85}\) = \(\frac{2.3}{Sin51}\)
r = \(\frac{2.3*Sin85}{sin51}\)
= 2.9483
r = 2.9 inches
Also, \(\frac{q}{SinQ}\) = \(\frac{s}{SinS}\)
\(\frac{q}{Sin44}\) = \(\frac{2.3}{Sin51}\)
q = \(\frac{2.3*Sin44}{Sin51}\)
= 2.0559
q = 2.0 inches
From Herons formula,
Area of a triangle = \(\sqrt{s(s-q)(s-r)(s-s)}\)
s = \(\frac{2.3 + 2.0 + 2.9}{2}\)
= 3.6
Area of ΔQRS = \(\sqrt{3.6(3.6-2.0(3.6-2.9)(3.6-2.3)}\)
= 2.2895
Area of ΔQRS = 2.3 square inches
Answer:
2.4
Step-by-step explanation:
9. Joseph is 2 meters 30 centimeters tall. How tall is Joseph in millimeters?
O23,000 millimeters
O2,300 millimeters
O230 millimeters
O23 millimeters
Answers
Answer:
Step-by-step explanation:
372 Millimeters
Answer:
2,300 millimeters
Step-by-step explanation:
when you convert 30 centimeters it’s 300 millimeters. When you convert 2 meters it’s 2,000 millimeters so…. That is the correct answer plus I just did the quiz and got it correct with that answer.
Question 2 The current report quantitatively analyzes three variables - load factors, revenue passenger mile, and available seat miles for American Airlines. The data retrieved for the analysis was extracted from the Bureau of Transportation Statistics, focusing on domestic flights from January 2006 to December 2012. The quantitative analysis focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. Table 2: Summary Statistics of American Airlines (Domestic) Revenue Passenger Miles Mean 6,624,897 Median 6,522,230 Mode NONE Minimum 5,208,159 Maximum 8,277,155 Standard Dev 720,158.571 Variance 518,628,367,282.42 Load Factors Mean 82.934 Median 83.355 Mode 84.56 Minimum 74.91 Maximum 89.94 Standard Dev 3.972 Variance 15.762 Revenue Passenger Miles 9000000 8000000 7000000 6000000 5000000 4000000 3000000 2000000 1000000 0 0 10 American Airlines (Domestic) Performance 20 30 ● Revenue Passenger Miles 40 50 Load Factors Available Seat Miles 60 Mean 7,984,735 Median 7,753,372 Mode NONE Minimum 6,734,620 Maximum 9,424,489 Standard Dev 744,469.8849 Variance 554,235,409,510.06 70 80 Linear (Revenue Passenger Miles) 90 100 Figure 1: American Airlines (Domestic) Performance Write a report based on the given data. Please include additional tests such as hypothesis testing, skewness, z statistic, level of significance, and other necessary tests, as well as a discussion of the results obtained.
Answers
The z-statistic test was conducted to determine the Deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
Report on the Analysis of American Airlines (Domestic) PerformanceThe quantitative analysis focused on three variables- load factors, revenue passenger miles, and available seat miles for American Airlines.
The Bureau of Transportation Statistics data for domestic flights from January 2006 to December 2012 was retrieved for the analysis. The quantitative analysis also focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. The results of the data are summarized in Table 2. Revenue Passenger Miles (RPM) mean is 6,624,897, the median is 6,522,230, and mode is NONE. The minimum is 5,208,159 and the maximum is 8,277,155. The standard deviation is 720,158.571, and the variance is 518,628,367,282.42.
Load Factors (LF) mean is 82.934, the median is 83.355, and mode is 84.56. The minimum is 74.91, and the maximum is 89.94. The standard deviation is 3.972, and the variance is 15.762. The Available Seat Miles (ASM) mean is 7,984,735, the median is 7,753,372, and mode is NONE. The minimum is 6,734,620, and the maximum is 9,424,489. The standard deviation is 744,469.8849, and the variance is 554,235,409,510.06.Figure 1 above displays the performance of American Airlines (Domestic).
The mean RPM is 7,984,735, and the linear regression line is y = 50584x - 2.53E+8. The linear regression line indicates a positive relationship between RPM and year, with a coefficient of determination, R² = 0.6806. A coefficient of determination indicates the proportion of the variance in the dependent variable that is predictable from the independent variable. Therefore, 68.06% of the variance in RPM is predictable from the year. A one-way ANOVA analysis of variance test was conducted to determine the equality of means of three groups of variables; RPM, ASM, and LF. The null hypothesis is that the means of RPM, ASM, and LF are equal.
The alternative hypothesis is that the means of RPM, ASM, and LF are not equal. The level of significance is 0.05. The ANOVA results indicate that there is a significant difference in means of RPM, ASM, and LF (F = 17335.276, p < 0.05). Furthermore, a post-hoc Tukey's test was conducted to determine which variable means differ significantly. The test indicates that RPM, ASM, and LF means differ significantly.
The skewness test was conducted to determine the symmetry of the distribution of RPM, ASM, and LF. The test indicates that the distribution of RPM, ASM, and LF is not symmetrical (Skewness > 0).
Additionally, the z-statistic test was conducted to determine the deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
For more questions on Deviation .
https://brainly.com/question/24298037
#SPJ8
A line segment has end points V (-4, -4) and W (11, 2). What is the x-coordinate of the point that is 2/5 of the way from V to W on this line segment?
Answers
After answering the presented question, we can conclude that We only coordinates need the positive solution, so t = 1.259
what are coordinate ?A coordinate in mathematics is a number or combination of integers that indicates the position of a point or object in space. Coordinates are often used to define the position of a point or object in a certain coordinate system, such as the Cartesian or polar coordinate systems. A point, for example, is located in the Cartesian coordinate system by its distance from the origin along the x-axis and its distance from the origin along the y-axis. These distances are denoted by two numbers, the x-coordinate and the y-coordinate, respectively. The two coordinates specify the point's position in the plane.
To find the point that is 2/5 of the way from V to W, w
\(d = \sqrt((x2 - x1)^2 + (y2 - y1)^2)\\\)
where (x1, y1) = (-4, -4) and (x2, y2) = (11, 2).\\
\(d = \sqrt((11 - (-4))^2 + (2 - (-4))^2)\\= \sqrt(15^2 + 6^2)\\= \sqrt(225 + 36)\\= \sqrt(261)\\\)
\(d1 = (2/5) * \sqrt(261)\\x = -4 + t * (11 - (-4))\\d1 = s\qrt((x - (-4))^2 + (y - (-4))^2)\\= \sqrt((x + 4)^2 + y^2 - 8x - 8y + 32)\\\)
\(d1^2 = (x + 4)^2 + y^2 - 8x - 8y + 32\\d1^2 = (x + 4)^2 + y^2 - 8x - 8y + 32\\= (x + 4)^2 + y^2 - 8(x + 4) - 8y + 64 \\d1^2 = (x + 4)^2 + y^2 - 8(x + 4) - 8y + 64\\= (x + 4)^2 + (y - 4)^2 + 4 )\\(2/5)^2 * 261 = (x + 4)^2 + (y - 4)^2 + 4\\\)
\(52.2 = (x + 4)^2 + (y - 4)^2 + 4\\(x + 4)^2 + (y - 4)^2 = 48.2\\(x + 4)^2 + y^2 - 8x - 8y + 32 = 48.2 \\(x + 4)^2 + (-4 + 6t)^2 - 8x + 48t - 32 = 48.2\\(x + 4)^2 + 36t^2 - 48t + 32 = 48.2\\(x + 4)^2 + 36t^2 - 48t - 16.2 = 0\\\)
Using the quadratic formula:
\(t = (48 + sqrt(48^2 - 4 * 36 * (-16.2))) / (2 * 36)\\= (48 + sqrt(2596.8)) / 72\\= (48 + 50.956) / 72\\t = 1.259 or t = -0.705\\\)
We only need the positive solution, so t = 1.259
To know more about coordinates visit:
https://brainly.com/question/27749090
#SPJ1