Answers
Answer:
-1/12
Step-by-step explanation:
change divide sign to multiply by reciprocating

Related Questions
What determines where the graph will cross the x-axis?.
Answers
The graph will cross the x-axis if the multiplicity of the real root is odd.
What is polynomial?
In arithmetic, a polynomial is an expression consisting of indeterminates and coefficients, that involves solely the operations of addition, subtraction, multiplication, and positive-integer powers of variables.
Main body:
For polynomials, the graph will cross the x-axis if the multiplicity of the real root is odd, and just touch the x-axis if the multiplicity of the real root is even. (The multiplicity of the root is the number of times it occurs as a root)
(a) y=(x+1)^2(x-2) The graph crosses at x=2 (multiplicity 1) but touches at x=-1 (mulitplicity 2)
(b) y=(x-4)^3(x-1)^2 The graph crosses at x=4 (multiplicity 3) but touches at x=1 (m=2)
(c) y=(x-3)^2(x+4)^4 The graph touches at x=3 and x=-4 as the multiplicities are both even.
The graphs: (a) black, (b) red, (c) green
To know more about polynomial , visit:
https://brainly.com/question/4142886
#SPJ4

so uh this is due tomorrow

Answers
The point P = (-5/3 squared, y) lies on the unit circle shown below. What is the value of
y in simplest form?

Answers
The required value of y for the unit circle is: 2/3
How to find the point on the unit circle ?The circle is defined as the locus of a point whose distance from a fixed point is constant i.e center (h, k).
The equation of the circle is given by:
(x - h)² + (y - k)² = r²
where:
h, k is the coordinate of the center of the circle on coordinate plane.
r is the radius of the circle.
Here,
Equation of the unit circle is given as,
x² + y² = 1
Now substitute the given value in the equation,
5/9 + y² = 1
y² = 1 - 5/9
y² = 4/ 9
y = √(4/9)
y = 2/3
Thus, the required value of y for the unit circle is 2/3
Read more about Unit Circle at: https://brainly.com/question/26284611
#SPJ1
Determine the equation of the parabola with focus
(
2
,
5
)
(2,5) and directrix
�
=
18
x=18.
Answers
The equation of the parabola with focus (2,5) and directrix x=18 is (x - 18)² + (y - 5)² = (y - (5 + (18 - 2) / 2))².
A parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating
straight line of that surface.
The focus of a parabola is a fixed point on the interior of a parabola used in the formal definition of the curve.
The directrix is a straight line perpendicular to the axis of symmetry and placed symmetrically with respect to the focus.
The axis of symmetry is the line through the focus and perpendicular to the directrix.
The vertex of a parabola is the point where its axis of symmetry intersects the curve. It is the point where the parabola changes direction or "opens
up" or "opens down.
The directrix is a fixed straight line used in the definition of a
parabola. It is placed such that it is perpendicular to the axis of symmetry and at a distance from the vertex equal to the
distance between the vertex and focus. It is the line that is equidistant to the focus and every point on the curve.Here's
the solution to the given problem:
The distance between the directrix and the focus is equal to p = 16 (since the directrix is x = 18, the parabola opens to the left, so the distance is measured horizontally)
The vertex is (h,k) = ((18+2)/2,5) = (10,5)
Then we can use the following formula: (x - h)² = 4p(y - k)
Substitute the vertex and the value of p. (x - 10)² = 64(y - 5)
Expand and simplify. (x - 10)² + (y - 5)² = 64(y - 5)
The equation of the parabola is (x - 10)² + (y - 5)² = 64(y - 5).
for such more question on parabola
https://brainly.com/question/17987697
#SPJ11
Six kids and two adults are going to the circus. Kid's tickets are on sale for only half the price of adult tickets. The total cost is $48. How much is one kids ticket? -how much is one adult ticket
Answers
Answer:
One kids ticket is $4.80 and one adult ticket is $9.60
Step-by-step explanation:
Create a system of equations where k is the cost of a kids ticket and a is the cost of an adult ticket:
6k + 2a = 48
k = 1/2a
Solve by substitution by substituting the second equation into the first one:
6k + 2a = 48
6(1/2a) + 2a = 48
Simplify and solve for a:
3a + 2a = 48
5a = 48
a = 9.6
Find the cost of a kids ticket by dividing this by 2, since they are on sale for half the price of adult tickets.
9.6/2
= 4.8
One kids ticket is $4.80 and one adult ticket is $9.60
find the points on the ellipse 3x2 2y2=1 where f(x,y)=xy has its extreme values.
Answers
The extreme values of f(x, y) = xy occur at the points (2, 1) and (-2, -1) on the ellipse \(3x^{2} +2y^{2} =1\).
To find the extreme values of f(x, y) = xy on the ellipse \(3x^{2} +2y^{2} =1\), we can use the method of Lagrange multipliers.
Define the function g(x, y) = \(3x^{2} +2y^{2} -1\). We need to find points (x, y) where the gradient of f is proportional to the gradient of g:
∇f = λ∇g
The gradient of f is ∇f = (y, x), and the gradient of g is ∇g = (6x, 4y). Therefore, we have the following system of equations:
y = 6λx
x = 4λy
Substitute the second equation into the first:
y = 6λ(4λy)
y = \(24λ^{2y}\)
If y ≠ 0, then 1 = \(24λ^{2}\), and λ = ±1/2. Plugging this value into the second equation gives x = ±2. Thus, we have two potential extreme points: (2, 1) and (-2, -1).
Now consider the case when y = 0. The constraint equation becomes \(3x^{2} =1\), and x = ±1/√3. However, these points correspond to f(x, y) = 0, which is not an extreme value.
Therefore, the extreme values of f(x, y) = xy occur at the points (2, 1) and (-2, -1) on the ellipse \(3x^{2} +2y^{2} =1\).
Know more about Extreme values here:
https://brainly.com/question/29667439
#SPJ11
Factor the quadratic expression completely.
8x^2-18x-5=8x
2
−18x−5=
Answers
The quadratic equation is `8x² - 18x - 5 = (8x - 5)(x - 1)`.Explanation: Here's how to factor the quadratic equation completely: 8x² - 18x - 5 is a quadratic equation.
Step 1: Multiply 8 and -5 together to get -40.Step 2: Find two numbers that have a product of -40 and a sum of -18. Since -20 and 2 have a product of -40 and a sum of -18, they're the two numbers we need.Step 3: Break the -18x term into -20x + 2x. Step 4: Rewrite the quadratic equation as follows: 8x² - 20x + 2x - 5 Step 5: Group the first two terms and the last two terms: 4x(2x - 5) + 1(2x - 5)Step 6: Factor out the (2x - 5) factor:(2x - 5)(4x + 1).
Therefore, the quadratic equation is factored completely into (8x - 5)(x - 1)
To know more about Quadratic visit-
https://brainly.com/question/22364785
#SPJ11
Consider two independent continuous random variables X1, X2 each uniformly distributed over [0, 2]. Let Y = max (X1, X2), i.e., the maximum of these two random variables. Also, let Fy (y) be the cumulative distribution function (CDF) of Y. Find Fy (y) where y = 0.72.
Answers
The CDF of Y evaluated at y = 0.72 is 0.1296.
Since X1 and X2 are independent and uniformly distributed over [0, 2], their joint density function is:
f(x1, x2) = 1/4, for 0 ≤ x1 ≤ 2 and 0 ≤ x2 ≤ 2
To find the CDF of Y, we can use the fact that:
Fy(y) = P(Y ≤ y) = P(max(X1, X2) ≤ y)
This event can be split into two cases:
X1 and X2 are both less than or equal to y:
In this case, Y will be less than or equal to y.
The probability of this occurring can be calculated using the joint density function:
P(X1 ≤ y, X2 ≤ y) = ∫0y ∫0y f(x1, x2) dx1 dx2
= ∫0y ∫0y 1/4 dx1 dx2
\(= (y/2)^2\)
\(= y^2/4\)
One of X1 or X2 is greater than y:
In this case, Y will be equal to the maximum of X1 and X2.
The probability of this occurring can be calculated as the complement of the probability that both X1 and X2 are less than or equal to y:
P(X1 > y or X2 > y) = 1 - P(X1 ≤ y, X2 ≤ y)
\(= 1 - y^2/4\)
Therefore, the CDF of Y is:
Fy(y) = P(Y ≤ y) = P(max(X1, X2) ≤ y)
= P(X1 ≤ y, X2 ≤ y) + P(X1 > y or X2 > y)
\(= y^2/4 + 1 - y^2/4\)
= 1, for y ≥ 2
\(= y^2/4,\)for 0 ≤ y ≤ 2
To find Fy(0.72), we simply substitute y = 0.72 into the expression for Fy(y):
\(Fy(0.72) = (0.72)^2/4 = 0.1296\)
For similar question on probability.
https://brainly.com/question/30403935
#SPJ11
Since X1 and X2 are uniformly distributed over [0, 2], their probability density functions (PDFs) are:
fX1(x) = fX2(x) = 1/2, for 0 <= x <= 2
To find the CDF of Y = max(X1, X2), we need to consider two cases:
1. If y <= 0, then Fy(y) = P(Y <= y) = 0
2. If 0 < y <= 2, then Fy(y) = P(Y <= y) = P(max(X1, X2) <= y)
We can find this probability by considering the complementary event, i.e., the probability that both X1 and X2 are less than or equal to y. Since X1 and X2 are independent, this probability is:
P(X1 <= y, X2 <= y) = P(X1 <= y) * P(X2 <= y) = (y/2) * (y/2) = y^2/4
Therefore, the CDF of Y is:
Fy(y) = P(Y <= y) =
0, y <= 0
y^2/4, 0 < y <= 2
1, y > 2
To find Fy(0.72), we substitute y = 0.72 into the CDF:
Fy(0.72) = 0.72^2/4 = 0.1296
Therefore, the value of Fy(y) at y = 0.72 is 0.1296.
Learn more about cumulative distribution function (CDF) here: brainly.com/question/31961014
#SPJ11
Symbolization in predicate logic. Put the following statements into symbolic notation, using the given letters as predicates. Existential quantifier and logical symbols are here for you to copy and paste: ∃x, ,V, ~, ,
Px: x is a strictly physical thing
Cx: x has consciousness
Sx: x has subjectivity
Mx: x is a mind
1. Nothing strictly physical has consciousness.
2. Minds exist.
3. All minds have consciousness and subjectivity.
4. No minds are strictly physical things.
Answers
The statements with symbolic notation using the given predicates logic are:
1. Nothing strictly physical has consciousness. ∀x(Px → ¬Cx)
2. Minds exist. ∃x(Mx)
3. All minds have consciousness and subjectivity. ∀x(Mx → (Cx ∧ Sx))
4. No minds are strictly physical things. ∀x(Mx → ¬Px)
What is a predicate logic and it's symbols?Predicate logic is a formal system of symbolic logic that extends propositional logic by introducing variables, predicates, quantifiers, and quantified statements. It allows for the representation and manipulation of relationships between objects, properties, and relations.
In predicate logic, symbols are used to represent various components:
1. Variables: Variables are used to represent individual elements or objects in a domain of discourse. They are typically denoted by lowercase letters such as x, y, z, and so on.
2. Predicates: Predicates are used to express properties or relations between objects. They are represented by uppercase letters followed by parentheses, such as P(x), Q(x, y), R(x, y, z), where x, y, z are variables.
3. Quantifiers: Quantifiers are used to express the scope of variables in a logical statement. The two main quantifiers are:
- Universal quantifier (∀): It is used to express that a statement holds for all elements in the domain. For example, ∀x P(x) means "For all x, P(x)."
- Existential quantifier (∃): It is used to express that there exists at least one element in the domain for which a statement holds. For example, ∃x P(x) means "There exists an x such that P(x)."
4. Logical symbols: Predicate logic uses logical symbols to represent logical connectives, negation, implication, and equivalence. The main logical symbols are:
- Conjunction (∧): Represents logical "and."
- Disjunction (∨): Represents logical "or."
- Negation (¬): Represents logical "not."
- Implication (→): Represents logical "if-then."
- Equivalence (↔): Represents logical "if and only if."
These symbols are used to construct complex logical statements by combining predicates, variables, and quantifiers. The goal is to provide a precise and formal language for reasoning about relationships and properties within a domain of discourse.
learn more about predicate logic: https://brainly.com/question/14914987
#SPJ4
SS ZONE
Block 5> Topic 3> Applications of Percent
Dre is painting a mural for his school.
Each can of spray paint costs $5 before
sales tax. The sales tax rate is 10%.
Plot a point that represents how Dre can
spend money on spray paint.
Cost Including Sales Tax (5)
132
88
44
20
40
60
Cost Before Sales Tax ($)

Answers
A point that represents how Dre can spend money on spray paint is plotted on the proportional relationship graphed at the end of the answer.
How to model the money spent?The money spent after sales tax is obtained multiplying the money spent before sales tax by a constant, hence a proportional relationship models the situation.
The general format of a proportional relationship is given as follows:
y = kx.
In which k is the constant of proportionality.
In this problem, the sales tax rate is of 10%, meaning that the total amount paid is composed as follows:
Cost before sales tax.10% of the cost before sales tax.Considering x as the cost before sales tax, the equation is given as follows:
y = x + 0.1x
y = 1.1x.
Meaning that one point is given as follows:
(5,5.5).
Meaning that when the cost before sales tax is of $5, the cost including sales tax is of $5.5.
More can be learned about proportional relationships at https://brainly.com/question/10424180
#SPJ1

a woman saw oranges and mangoes at the market. She bought some oranges at 35 cents each and some mangoes at $1.00 each. If she bought a total of 25 fruits which had a total cost of $12.00. How much of each fruits did she buy?
Answers
The number of oranges and the number of mangoes that she bought will be 20 and 5.
What is the linear system?A linear system is one in which the parameter in the equation has a degree of one. It might have one, two, or even more variables.
A woman saw oranges and mangoes at the market.
She bought some oranges at 35 cents each and some mangoes at $1.00 each.
If she bought a total of 25 fruits which had a total cost of $12.00.
Let x be the number of oranges and y be the number of mangoes.
Then the equations will be
x + y = 25 ...1
0.35x + y = 12 ...2
By solving equations 1 and 2, we have
x = 20 and y = 5
More about the linear system link is given below.
https://brainly.com/question/20379472
#SPJ1
3. Celine is knitting a scarf. The finished length will be 1.2 meters. So far
she has knitted 0.8 meters. How many more meters does Celine
need to knit? Draw a number line to solve.
Answers
Celine has already knitted 0.8 meters. Her final result should be 1.2 meters.
To calculate how many meters Celine has to knit we should subtract the already knitted length of scarf from the entire length. This give the equation:
\(x=1.2m-0.8m\)
x is the unknown
x = 0.4 meters
Simplify the following expression.
(-12x³-48x²)+ -4x
A. -3x*- 12x³
B. 3x² + 12x
C. 16x² +52x
D. -16x* - 52x³
Please select the best answer from the choices provided
Answers
Answer:
Step-by-step explanation:
To simplify the expression (-12x³ - 48x²) + (-4x), we can combine like terms by adding the coefficients of the same degree of x.
The like terms in the expression are the terms with x³, x², and x. Let's combine them:
-12x³ + (-4x) = -12x³ - 4x
-48x² + 0 = -48x²
Now, combining these two results, we have:
(-12x³ - 4x) + (-48x²) = -12x³ - 4x - 48x²
Therefore, the simplified expression is -12x³ - 4x - 48x².
None of the provided choices match the simplified expression.
Please Helppppppppppp

Answers
Answer:
The width of the actual pool is 12 meters
Step-by-step explanation:
You can put Kiara's scale into a ratio or fraction to help visualize it better: 13/6. Now, let's put what we do know for the other ratio into a fraction. we know that the pool is 26 centimeters wide, and since the 26 matches with the 13, that goes in the numerater. since we don't know the denominator, we can just put 26/x (you can use whatever letter you like but I'll use x here)
So in order to get 13/6 to 26/x, we need to find how to figure out what we are doing to the original fraction. Since 13 x 2= 26, it looks like we are multiplying the ratios by 2. Now that we know that, we can multiply the denominator (6) by 2 to equal 12, our answer.
Hope this helps :)
Alan and Bree are taking a keyboarding test. The tables show the number of words they type over time, and the numbers of mistakes they make
Mistakes
Alan's Typed
Words
5
10
Time
(seconds)
6
12
2
4
6
18
15
20
8
Mistakes
Bree's Typed
Words
9
Time
(seconds)
8
3
6
18"
16
9
27
36
24
32
12
Who makes mistakes at a faster rate? Explain using ratios.
Select the answers from the drop-down lists to correctly complete the sentences.
Answers
Answer:
Bree does
Step-by-step explanation:
Find the surface area of the portion S of the cone z^2 = x^2 + y^2 where z>/ 0 contained within the cylinder y^2 + z^2 < 1
Answers
The surface area of the portion S of the cone z^2 = x^2 + y^2 where z>/ 0 contained within the cylinder y^2 + z^2 < 1 is 8π.
The cone is defined by the equation z^2 = x^2 + y^2.
The cylinder is defined by the equation y^2 + z^2 < 1.
The intersection of the cone and the cylinder is a surface that is part of a cone and part of a cylinder.
The surface area of the cone is given by the formula A = πr^2h, where r is the radius of the base and h is the height of the cone.
The radius of the base of the cone is equal to 1, and the height of the cone is equal to √2. Therefore, the surface area of the cone is π(1)^2(√2) = √2π.
The surface area of the cylinder is given by the formula A = 2πrh, where r is the radius of the base and h is the height of the cylinder.
The radius of the base of the cylinder is equal to 1, and the height of the cylinder is equal to 1. Therefore, the surface area of the cylinder is 2π(1)(1) = 2π.
The surface area of the intersection of the cone and the cylinder is equal to the surface area of the cone minus the surface area of the cylinder. Therefore, the surface area of the intersection is √2π - 2π = 8π.
To learn more about cones click here: brainly.com/question/32148386
#SPJ11
the length of a vegetable garden is 3 feet longer than its width. if the area of the garden is 154 square feet, find its dimensions.
Answers
The dimensions of the vegetable garden are :
Length = 14 feet
Width = 11 feet
Let's start by using the formula for the area of a rectangle:
Area = Length x Width
We know that the area of the vegetable garden is 154 square feet, so we can plug that in:
154 = Length x Width
Next, we're given that the length is 3 feet longer than the width, so we can write:
Length = Width + 3
We can substitute that expression for Length into the area formula:
154 = (Width + 3) x Width
Expanding the brackets:
154 = Width^2 + 3Width
Now we have a quadratic equation, which we can solve by either factoring or using the quadratic formula. I'll use the quadratic formula here:
First, we need to put the equation into standard form (ax^2 + bx + c = 0):
Width^2 + 3Width - 154 = 0
a = 1, b = 3, c = -154
Plugging those values into the quadratic formula:
Width = (-b ± sqrt(b^2 - 4ac)) / 2a
Width = (-3 ± sqrt(3^2 - 4(1)(-154))) / 2(1)
Width = (-3 ± sqrt(625)) / 2
We can simplify the square root:
Width = (-3 ± 25) / 2
So we have two possible solutions:
Width = 11 or Width = -14
Since we're dealing with a physical garden, the width can't be negative, so we'll discard that solution.
Now we can use the expression for Length that we found earlier:
Length = Width + 3
Length = 11 + 3 = 14
So the dimensions of the vegetable garden are 11 feet by 14 feet.
To learn more about area of a rectangle visit : https://brainly.com/question/2607596
#SPJ11
The table below shows the number of
different drinks ordered at a coffee morning.
One of the drinks is chosen at random.
a) Work out P(small coffee).
b) Work out P(coffee small).
Give each answer as a fraction in its
simplest form.
Small
Large
Total
Tea
16
5
21
Coffee
6
7
13
Total
22
12
34

Answers
a) The conditional probability is: 6/13
b) The conditional probability is: 6/22
Given data ,
a)
To find P(small | coffee), we use the formula for conditional probability or the Bayes theorem.
P(small | coffee) = P(small and coffee) / P(coffee)
where the likelihood that an event will occur based on the likelihood that a comparable outcome will occur in the future.
And , P ( A | B ) = [ P ( B | A ) P ( B ) ] / P ( A )
P ( small | coffee ) = ( 6/34 )
P(coffee) = ( 13/34 )
So, P(small | coffee) = 6/13
b)
The conditional probability is:
P ( coffee | small ) = P(coffee and small) / P(small)
P ( coffee | small ) = 6/22
Hence , the Bayes theorem is solved.
To learn more about Bayes theorem click :
https://brainly.com/question/29598596
#SPJ1
If a watch costs $40 and you must pay 6.5 % sales tax, how much will the tax be?
A
$16.50
B
$6.50
C
$26.00
D
$2.60
I'M SO CONFUSED :( PLZ HELP ME
Answers
Answer:
D $2.60
Step-by-step explanation:
because 6.5% of 40 is 2.6
hope this helps
plz can i get brainliest
Consider the surface f(x,y,z)=x5z6 sin(y4z6) 2=0. Find the following partial derivatives
Answers
The partial derivatives are:
∂ z / ∂ x = − [ 5x⁴z⁶ ] / [ 6x⁵z⁵ + 6z⁵y⁴cos ( y⁴z⁶ )]
∂ z / ∂ y = − [ 4y³z⁶ cos ( y⁴ z⁶ ) ] / [ 6x⁵z⁵ + 6z⁵y⁴cos ( y⁴z⁶ )]
We have,
f(x, y, z) = x⁵z⁶ + sin (y⁴z⁶) + 2 = 0
Now, partially differentiating we get
∂ z / ∂ x
= - [ ∂ F / ∂ x ] / [ ∂ F / ∂ z ]
= − [ 5x⁴z⁶ ] / [ 6x⁵z⁵ + 6z⁵y⁴cos ( y⁴z⁶ )]
and,
∂ z / ∂ y
= - [ ∂ F / ∂ y ] / [ ∂ F / ∂ z ]
= − [ 4y³z⁶ cos ( y⁴ z⁶ ) ] / [ 6x⁵z⁵ + 6z⁵y⁴cos ( y⁴z⁶ )]
Learn more about Partial derivative Here:
https://brainly.com/question/31397807
#SPJ4
Which graph represents a relation that is NOT a function
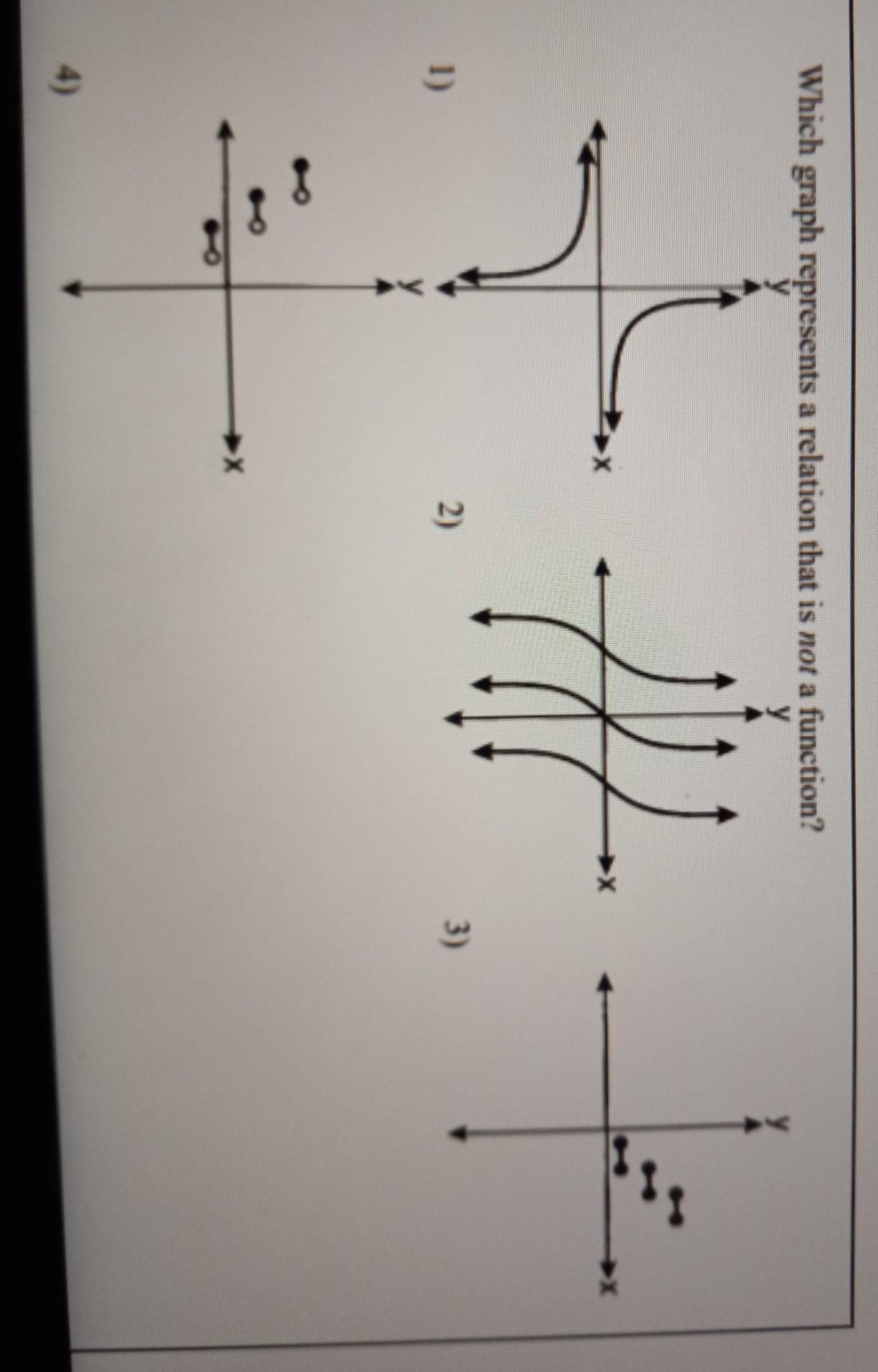
Answers
Answer:
3) if you were to draw vertical lines through this graph you would have instances where an 'x' value would have more than one unique 'y' value
Step-by-step explanation:
functions must have one unique 'y' value for each 'x' value
The third graph represent a relation that is not a function
What is a function?A relation is a function if it has only One y-value for each x-value.
The third one doesn't represent a function, because for some values of "x", you get two different values for "y" (which should not happen, if that were a function).
In order to see it better, you can trace a vertical line onto that graph.
If that line and the graph intersects in more than one point, then that graph doesn't represent a function.
In every function, you must have a single "y" value for each "x" in the domain.
Hence, the third graph represent a relation that is not a function
To learn more on Functions click:
https://brainly.com/question/21145944
#SPJ2
A party planner organized a dinner party. The party planner recorded the height of the candlesticks over time and graphed the relationship.
graph with the x axis labeled time in hours and the y axis labeled height of candlestick in inches and a line going from the point 0 comma 8 through the point 3 comma 6
Find and interpret the slope and y-intercept in this real-world situation.
A. The slope is 8, and the y-intercept is negative two thirds. The candle starts at a height of two thirds of an inch and decreases 8 inches every hour.
B. The slope is 8, and the y-intercept is negative three halves. The candle starts at a height of three halves of an inch and decreases 8 inches every hour.
C. The slope is negative two thirds, and the y-intercept is 8. The candle starts at a height of 8 inches and decreases two thirds of an inch every hour.
D. The slope is negative three halves, and the y-intercept is 8. The candle starts at a height of 8 inches and decreases three halves of an inch every hour.
Answers
C. The slope is negative two-thirds, and the y-intercept is 8. The candle starts at a height of 8 inches and decreases two-thirds of an inch every hour.
What are lines and their slopes?We know lines have various types of equations, the general type is
Ax + By + c = 0, and the equation of a line in slope-intercept form is
y = mx + b.
Where slope = m and b = y-intercept.
the slope is the rate of change of the y-axis with respect to the x-axis and the y-intercept is the (0,b) where the line intersects the y-axis at x = 0.
The relationship of the candlestick between height and time is represented by a straight line passing through the points (0, 8) and (3, 6).
Slope(m) = (6 - 8)/(3 - 0).
Slope(m) = - 2/3.
Taking any of the points we have,
6 = - (2/3)×3 + b.
6 = - 2 + b.
b = 8.
y = - (2/3)x + 8.
learn more about lines and slopes here :
https://brainly.com/question/3605446
#SPJ1
3x1 + 2x2 = 5 5x1 + x2 = 8 Solve the set of linear algebraic equations using the "Gauss-Seidel Method" by X1(0) = x2(0) = 0 taking with an accuracy of & < 0,03
Answers
In the first iteration, we obtained approximate values of x1(1) ≈ 1.67 and x2(1) = 8. In the second iteration, we updated the values to x1(2) ≈ -3.67 and x2(2) ≈ 26.35. In the third iteration, the values were further updated to x1(3) ≈ -38.77 and x2(3) ≈ 198.85.
To solve the set of linear algebraic equations using the Gauss-Seidel method with the given initial values and accuracy requirement, we can follow these steps:
Step 1: Rearrange the equations in terms of x1 and x2:
Equation 1: 3x1 + 2x2 = 5
Equation 2: 5x1 + x2 = 8
Step 2: Write the equations in iterative form:
Equation 1: x1(k+1) = (5 - 2x2(k)) / 3
Equation 2: x2(k+1) = (8 - 5x1(k)) / 1
where x1(k) and x2(k) represent the initial values and x1(k+1) and x2(k+1) represent the updated values in the kth iteration.
Step 3: Initialize the values and set the desired accuracy:
Let x1(0) = 0 and x2(0) = 0 (given initial values)
Set the desired accuracy as ε = 0.03
Step 4: Perform iterations until the desired accuracy is reached:
Iterate the following steps until the condition |x1(k+1) - x1(k)| < ε and |x2(k+1) - x2(k)| < ε are satisfied:
- Calculate the updated values using the iterative equations:
x1(k+1) = (5 - 2x2(k)) / 3
x2(k+1) = (8 - 5x1(k)) / 1
- Calculate the differences:
Δx1 = |x1(k+1) - x1(k)|
Δx2 = |x2(k+1) - x2(k)|
- Check if the differences are less than ε:
If Δx1 < ε and Δx2 < ε, exit the iteration.
Step 5: Output the solution:
The solution will be the values of x1 and x2 obtained in the final iteration.
Let's perform the iterations:
Iteration 1:
x1(1) = (5 - 2x2(0)) / 3 = (5 - 2(0)) / 3 ≈ 1.67
x2(1) = (8 - 5x1(0)) / 1 = (8 - 5(0)) / 1 = 8
Iteration 2:
x1(2) = (5 - 2x2(1)) / 3 = (5 - 2(8)) / 3 ≈ -3.67
x2(2) = (8 - 5x1(1)) / 1 = (8 - 5(-3.67)) / 1 ≈ 26.35
Iteration 3:
x1(3) = (5 - 2x2(2)) / 3 = (5 - 2(26.35)) / 3 ≈ -38.77
x2(3) = (8 - 5x1(2)) / 1 = (8 - 5(-38.77)) / 1 ≈ 198.85
To know more about Gauss-Seidel Method related question visit:
https://brainly.com/question/13567892
#SPJ11
Distribute and simplify these radicals.

Answers
Answer:
D) \(6+2\sqrt{6}\)
Step-by-step explanation:
\(2\sqrt{3} *(\sqrt{2} +\sqrt{3} )\\\\6+2\sqrt{6}\)
Without multiplying, order the following products from least to greatest.
1 1/6 x 310 8/8x310 4/7x310
Answers
One of the factors is present in all of the items mentioned. The order of the value of the other factor will match the order of the value of the product.
A multiplication comparison: What does that mean?When two amounts are compared, a multiplicative comparison determines which can be created when the other is multiplied by a specific number. Like Sam, who has twice as many balloons than Sid. Three balloons are in Sid's possession.Every single one of the previously named things contains one of the elements. Both the order of the other factor's value and the order of the product's value will be the same. A fraction that is equal to 1 multiplied by a number produces a number as the result. A positive whole number can be multiplied by a fraction greater than one, and the resulting number will always be larger than the initial whole number.To learn more about Multiplicative comparison refer to:
https://brainly.com/question/171046
#SPJ1
please help me......
write in y=mx+b form

Answers
Answer:
What?
Step-by-step explanation:
D.
Kierston needs to paint a wall of the youth center. She knows that 1 can of paint covers an area of 2.2 square meters. Kierston measures the wall using a meter stick as shown below. How many cans of paint must kierston buy to paint the wall of the youth center?
Answers
Answer:
See Explanation
Step-by-step explanation:
Given
\(1\ can = 2.2m^2\)
Required
Determine the number of cans for the wall
The dimension of the wall is not given. So, I will use the following assumed values:
\(Length=20m\)
\(Width = 44m\)
First, calculate the area of the wall
\(Area = Length * Width\)
\(Area = 20m * 44m\)
\(Area = 880m^2\)
If \(1\ can = 2.2m^2\)
Then \(x = 880m^2\)
Cross Multiply:
\(x * 2.2m^2 = 1 * 880m^2\)
\(x * 2.2m^2 = 880m^2\)
\(x * 2.2 = 880\)
Make x the subject
\(x = \frac{880}{2.2}\)
\(x = 400\)
400 cans using the assume dimensions.
So, all you need to to is, get the original values and follow the same steps
2 3/4 is between the whole number_____and_____
Answers
Answer: 2 and 3
Step-by-step explanation:
Let (G₁, +) and (G2, +) be two subgroups of (R, +) so that Z+ C G₁ G₂. If : G₁ G₂ is a group isomorphism with o(1) = 1, show that o(n) = n for all ne Zt. Hint: consider using mathematical induction.
Answers
To prove that o(n) = n, we will use mathematical induction to show that φ(n) has an order of n for any positive integer n.
We proceed with mathematical induction.
Base Case: For n = 1, φ(1) = 1, and since φ(1) = 1, the order of φ(1) is indeed 1.
Inductive Step: Assume that for some k ≥ 1, the order of φ(k) is k. We need to prove that the order of φ(k+1) is k+1.
Since φ is a group isomorphism, φ(k+1) = φ(k) + φ(1). By the induction hypothesis, the order of φ(k) is k. Additionally, φ(1) = 1, so the order of φ(1) is 1.
Now, suppose the order of φ(k+1) is m. This means that (φ(k+1))^m = e, where e is the identity element in G₂.
Expanding this, we have (φ(k) + φ(1))^m = e. By applying the binomial theorem, we can show that (φ(k))^m + m(φ(k))^(m-1)φ(1) + ... = e.
Since φ(k) has an order of k, (φ(k))^k = e, and all other terms in the expansion have an order higher than k. Thus, we can simplify the equation to (φ(k))^k + m(φ(k))^(m-1)φ(1) = e.
Since φ(1) = 1, the term m(φ(k))^(m-1)φ(1) reduces to m(φ(k))^(m-1). But φ(k) has an order of k, so (φ(k))^(m-1) has an order of k. Hence, m(φ(k))^(m-1) = 0. Since e is the identity element, this implies m = 0.
Therefore, the order of φ(k+1) is k+1, which completes the inductive step.
By mathematical induction, we have proven that for all positive integers n, the order of φ(n) is n.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ11
what are important of mountain ?
Answers
Answer:
hlw its jess
your answer is here
Mountains are particularly important for their biodiversity, water, clean air, research, cultural diversity, leisure, landscape and spiritual values.Step-by-step explanation:
hope it may help you
mark as brainlist please