Answers
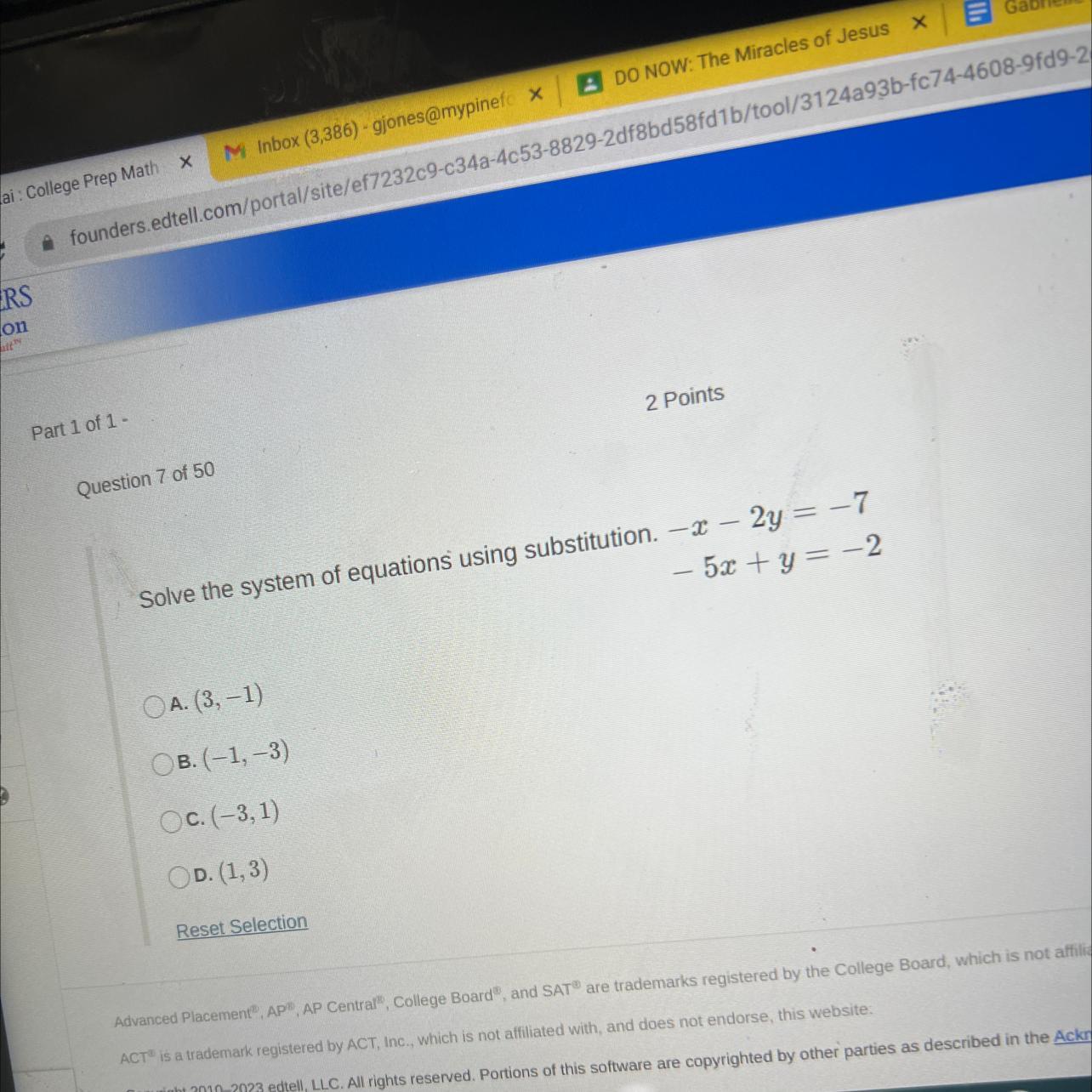
The value of x and y using substitution method is (1, 3).
How to find the system of equation?System of equation can be solved using different method such as substitution method, elimination method and graphical method.
Let's solve the system of equation by substitution method.
Therefore,
-x - 2y = - 7
-5x + y = - 2
Hence,
x = -2y + 7
substitute the value of x in equation(ii)
-5(-2y + 7) + y = - 2
10y - 35 + y = -2
11y = -2 + 35
11y = 33
divide both sides by 11
y = 33 /11
y = 3
Hence,
x = -2(3) + 7
x = -6 + 7
x = 1
Therefore,
x = 1
y = 3
learn more on system of equation here: https://brainly.com/question/29263329
#SPJ1
Related Questions
URGET PLEASE HELP!!!!!!!!!!!!!!!!!

Answers
It is the bottom left one
It is an absolute value graph, so the line should be a y = x graph but all y values are positive.
the bottom left one shows the same line with the y increased by 5
let r=(x2 y2)1/2 and consider the vector field f→=ra(−yi→ xj→), where r≠0 and a is a constant. f→ has no z-component and is independent of z.
Answers
The vector field F → = r a ( -y i → + x j → ) has no z-component and is independent of z, indicating that it lies entirely in the xy-plane and does not vary along the z-axis.
The vector field is given by:
F → = r a ( -y i → + x j → )
where \(r = \sqrt{(x^2 + y^2)}\) and a is a constant.
We can rewrite this vector field in terms of its components:
F → = ( r a ( -y ) , r a x )
To show that the vector field F → has no z-component and is independent of z, we can take the partial derivatives with respect to z:
∂ F x / ∂ z = 0
∂ F y / ∂ z = 0
Both partial derivatives are zero, which means that the vector field F → does not depend on z and has no z-component. Therefore, it is independent of z.
This indicates that the vector field F → lies entirely in the xy-plane and does not vary along the z-axis. Its magnitude and direction depend on the values of x and y, as determined by the expressions \(r = \sqrt{(x^2 + y^2)}\)) and the constant vector a.
In summary, the vector field F → = r a ( -y i → + x j → ) has no z-component and is independent of z, indicating that it lies entirely in the xy-plane and does not vary along the z-axis.
Learn more about vector calculus here:
brainly.com/question/10164701
#SPJ4
for a vector space v and a finite set of vectors s = {v1, · · · , vn} in v , copy down the definitions for a) span(
Answers
(a) Span (s) = {a₁v₁+a₂v₂+.........aₙvₙ} \(a_i\) ∈ field.
(b) A basic for V is linearly independent spanning set of V.
(c) A subset of V which its self is a vector space is called subspace of V.
Let V be a vector space and S be a set of vectors on i. e.
s{V₁,V₂,V₃..........Vₙ} then,
(a) Span (S) is set of all possible linear combinations of vector in S i.e.
Span (s) = {a₁v₁+a₂v₂+.........aₙvₙ} \(a_i\) ∈ field
i. e. \(a_i\) are scalars from field on which vector space V is defined.
(b) A basic for V is linearly independent spanning set of V i.e.
Let B be set of vectors in V. then B is a Basic of V if
(i) B is linearly independent set
(ii) Span (B) = V
(C) A subset of V which its self is a vector space is called subspace of V.
Therefore, Span (s) = {a₁v₁+a₂v₂+.........aₙvₙ} \(a_i\) ∈ field.
Learn more about vector here:
https://brainly.com/question/32510686
#SPJ4
Incomplete Question:
for a vector space v and a finite set of vectors s = {v1, · · · , vn} in v , copy down the definitions for
a) span(S).
b) a basis of b.
c) a subspace of V.
Clase de estadistica la moda es una medida de tendencia central que: ¿por que? a) tiene muchos datos b) tiene la mayor frecuencia c) tiene poca frecuencia d) al ordenar los datos de menor a mayor es el dato que se ubica en el centro
Answers
Answer:
b) tiene la mayor frecuencia
Step-by-step explanation:
Las medidas de tendencia central se refieren a un centro alrededor del cual se encuentran todos los datos y estas medidas son: la media, la moda y la mediana. La media es el valor promedio de un grupo de datos, la moda es el dato que se repite más veces y la mediana es el valor que se encuentra en el centro cuando los datos se ubican de menor a mayor. De acuerdo a esto, la respuesta es que la moda es una medida de tendencia central que tiene la mayor frecuencia.
Los otras opciones no son correctas porque el tamaño del conjunto de datos no depende de las medidas de tendencia central, esto depende de cada situación y pueden ser muchos o pocos datos. Además la opción "al ordenar los datos de menor a mayor es el dato que se ubica en el centro" se refiere a la mediana.
A group of friends were working on a student film. They spent $504 on props, which was 42% of their total budget. What was the total budget for their student film?
Answers
In how many ways can the numbers 3, 4, 5, 6, 7, 8, 9, and 10 be divided into two sets A and B such that the sum of the numbers in B is three times the sum of the numbers in A?
Answers
Answer:
4 ways
Step-by-step explanation:
3+4+5+6+7+8+9+10=52
1/4×52=13
13×3=39
3+10=13
4+9=13
5+8=13
6+7=13
so there are 4 ways to divide in two parts.
1.
A={3,10}
B={4,5,6,7,8,9}
2.
A={4,9}
B={3,5,6,7,8,10}
3.
A={5,8}
B={3,4,6,7,9,10}
4.
A={6,7}
B={3,4,5,8,9,10}
what are the vertices of this ellipse? graph (-4, 2) and (4, 2) (2 , 2) and (2 , 2) (-5, 5) and (-5, -1) (-9, 2) and (-1, 2)
Answers
The vertices of the ellipse are (-4,2) and (4,2), since these points lie on the major axis of the ellipse which is horizontal.
Two of the focuses given in the issue, (−4,2) and (4,2), are both situated on a similar even line. This implies that the significant hub of the oval should be level. Two different focuses given in the issue, (2,2) and (- 9,2), are likewise situated on this level line. Thusly, the focal point of the oval is the midpoint between the focuses (- 4,2) and (4,2), which is (0,2).
The other two focuses given in the issue, (−5,5) and (−5,−1), are situated on an upward line that goes through the focal point of the oval. This implies that the minor pivot of the oval should be vertical.
The vertices of the oval are the places where the significant hub meets the circle. Since the significant hub goes through the focuses (−4,2) and (4,2), the vertices of the oval are (- 4,2) and (4,2).
In this way, the vertices of the oval are (- 4,2) and (4,2).
To learn more about vertices of ellipse, refer:
https://brainly.com/question/9525569
#SPJ4
tyler can type twice as many words wpm as kyla
define variable=
Expression to represent problem=
if kyla can type 3 wpm how many wpm can Tyler type
Answers
Answer:
Your answer is: 6 wpm
Step-by-step explanation:
If Tyler types twice as fast as Kyla, you multiply the amount of wpm Kyla writes by 2. 3 multiplied by 2 equals 6. Therefore, Tyler writes 6 wpm.
a) A circular channel section has diameter of 6m and it is running half. Calculate the discharge through the channel if the bed slope is 1 in 600 and manning’s co efficient is equal to 0.014.
Answers
To calculate the discharge through the circular channel, we can use Manning's equation, which relates the flow rate (Q) to the channel properties and flow conditions. Manning's equation is given by:
Q = (1/n) * A * R^(2/3) * S^(1/2)
where:
Q is the discharge (flow rate)
n is Manning's coefficient (0.014 in this case)
A is the cross-sectional area of the channel
R is the hydraulic radius of the channel
S is the slope of the channel bed
First, let's calculate the cross-sectional area (A) of the circular channel. The diameter of the channel is given as 6m, so the radius (r) is half of that, which is 3m. Therefore, the area can be calculated as:
A = π * r^2 = π * (3m)^2 = 9π m^2
Next, let's calculate the hydraulic radius (R) of the channel. For a circular channel, the hydraulic radius is equal to half of the diameter, which is:
R = r = 3m
Now, we can calculate the slope (S) of the channel bed. The given slope is 1 in 600, which means for every 600 units of horizontal distance, there is a 1-unit change in vertical distance. Therefore, the slope can be expressed as:
S = 1/600
Finally, we can substitute these values into Manning's equation to calculate the discharge (Q):
Q = (1/0.014) * (9π m^2) * (3m)^(2/3) * (1/600)^(1/2)
Using a calculator, the discharge can be evaluated to get the final result.
To learn more about coefficient : brainly.com/question/1594145
#SPJ11
PLZ HELP THIS ONE THERES A PIC DOWN BELOW. plz :)

Answers
it's pretty simple 678910 are greater and -4 -3 -2 -1 are too because they are closer to the whole than 5 is
Answer:
Open circle at 0 arrow to the left
Open circle at 5 arrow to the right
Step-by-step explanation:
numbers that are negative is asking for everything to the left of 0. not inclusive though because 0 is not negative.
Open circle at 0 arrow to the left
Numbers greater than 5 will be to the right of five. Not inclusive because it doesn't ask for numbers equal to 5 too.
Open circle at 5 arrow to the right
If quadrilateral JKLM had a translation where all the vertices were in the second quadrant, what would be the vertices?

Answers
3. The range of (x) = 2(x - 1) - 6 is
a. {YER/y > -6}
b. {YER/y
c. {YER/y < -6}
d. {YER/y > -1}
e. {YER}
Answers
Answer:d
Step-by-step explanation:
PLS HELP ASAP FOR BRAINLIEST

Answers
Answer: x=45
Step-by-step explanation:
Solve for c get 20 c=b so b+115 =135 180-135=x
Answer:
x=45
Step-by-step explanation:
160=115+x (use vertical angles)
subtract 115 from both sides
160-115=45
x=45
The estimated product of 20.7 and 9.18, after rounding both factors to the nearest whole number, is . The exact product of 20.7 and 9.18 has decimal places.
Answers
Answer:
Estimated=189
Exact=190.026
Step-by-step explanation:
Estimated values
20.7 to nearest whole number= 21
9.18 to nearest whole number= 9
Product means multiplication
Estimated product of 20.7 and 9.18
=21×9
=189
Exact product of 20.7 and 9.18
=20.7 × 9.18
=190.026
It has 3 decimal places
Answer:
The estimated product of 20.7 and 9.18, after rounding both factors to the nearest whole number,
is
✔ 189
.
The exact product of 20.7 and 9.18 has
✔ 3
decimal places.
Step-by-step explanation: Hope this helps(:
3(-4/7) I don’t know how to get the answer
Answers
Answer:
Step-by-step explanation:
if its 3 - 4/7 then it = 2 3/7
if its 3*-4/7 then it = -12/7 = - 1 5/7
Carlisle Transport had $4,520 cash at the beginning of the period. During the period, the firm collected $1,654 in receivables, paid $1,961 to supplier, had credit sales of $6,916, and incurred cash expenses of $500. What was the cash balance at the end of the period?
Answers
To calculate the cash balance at the end of the period, we need to consider the cash inflows and outflows.
Starting cash balance: $4,520
Cash inflows: $1,654 (receivables collected)
Cash outflows: $1,961 (payments to suppliers) + $500 (cash expenses)
Total cash inflows: $1,654
Total cash outflows: $1,961 + $500 = $2,461
To calculate the cash balance at the end of the period, we subtract the total cash outflows from the starting cash balance and add the total cash inflows:
Cash balance at the end of the period = Starting cash balance + Total cash inflows - Total cash outflows
Cash balance at the end of the period = $4,520 + $1,654 - $2,461
Cash balance at the end of the period = $4,520 - $807
Cash balance at the end of the period = $3,713
Therefore, the cash balance at the end of the period is $3,713.
To learn more about cash : brainly.com/question/31754110
#SPJ11
6 A cube has a surface area of 54 mm². The length of its sides is: A 3 mm B 4 mm C 5
mm D 6 mm E 7 mm
Answers
Answer:
A
Step-by-step explanation:
A cube has 6 square faces
given surface area = 54 mm² , then
area of one face = 54 mm² ÷ 6 = 9 mm²
the area (A) of a square is calculated as
A = s² ( s is the side length ) , so
s² = 9 ( take square root of both sides )
s = \(\sqrt{9}\) = 3 mm
Can someone please explain this to me?

Answers
Answer:
62°
Step-by-step explanation:
Angle KPO = 90°. If you add angles KPN and NPO together, you will get 90°. Set up an equation and solve for x.
2x + x - 3 = 90
3x - 3 = 90
3x - 3 + 3 = 90 + 3
3x = 93
3x/3 = 93/3
x = 31
Now solve for the measure of KPN by substituting 31 for x.
KPN = 2x
KPN = 2(31)
KPN = 62°
Answer:
D 62
Step-by-step explanation:
Good luck
Fawn ran a 5-kilometer race in 66 minutes. To the nearest hundredth, what was her speed in meters per second?
A.
1.26
B.
0.08
C.
0.13
D.
75.76
Answers
5 km = 5000 meters
66 minutes = 3960 seconds
Meters per second = 5000/3960 = 1.26
The answer is A.1.26
Use ratios to convert each measurement.
1. 3 yards = _____ feet
2. _____ cups= 5 gallons
3. 72 inches =_____ yards
4. ______ ounces = 5 pounds
5. ______ inches =7 feet
6. 24 feet = _____ yards
7. 40 pints = ______ gallons
8. 16 cups = ______ quarts and
9. ________ inches = 4 yards
10. 48 ounces = ________ Pounds
Answers
Answer:
1. 3 yards= 9 feet
2. 78 cups=5 gallons
3. 72 inches = 2 yards
4. 80 ounces = 5 pounds
5. 84 inches = 7 feet
6. 24 feet = 8 yards
7. 40 pints = 5 gallons
8. 16 cups = 5 quarts
9. 144 inches = 4 yard
10. 48 ounces = 3 pounds
Which of the following expressions are equivalent to 6 + (-4) - 5?
Choose 2 answers
A. −(−6+4)−5
B. 6−4−(−5)
C. 6−(4+5
D.6+4−5
E. −(−6)+(−4)−(−5)
Answers
What is the value of x? enter your answer in the box. x = cm
Answers
The value of x in the given equation will be 2/5
From the data,
We have to determine the value of x.
The given equation is: 18x-16=-12x-4
For determining the value of x, we will first shift the like terms on one side of the equation.
So, for solving the value of x we will shift the terms containing x and the constant on both sides of the equation.
So, shifting -12x from the right-hand side of the equation to the left-hand side of the equation,
We will get it as:
18x+12x = -4+16
30x=12
Now for solving the value of x we will shift x from the left side of the equation to the right side of the equation.
So, the value of x will be = 12/30 = 2/5
For more questions on Equation
https://brainly.com/question/25678139
#SPJ4
The correct question may be:
What is the value of x
18x-16=-12x-4
Enter your answer in the box.
HELP ME!!! 20 points!!

Answers
I don’t know helppp
Me

Answers
\(f(x) = -2(x - 0.5)^2 + 6\) is the equation of the quadratic function that passes through the points (-1, 14), (0, 8), (1, 6), and (2, 8).
What is quadratic function?
f(x) = ax2 + bx + c, where a, b, and c are numbers with a not equal to zero, is a quadratic function.
To find the equation of the quadratic function that passes through the points (-1, 14), (0, 8), (1, 6), and (2, 8), we can use the vertex form of the quadratic function, which is:
\(f(x) = a(x - h)^2 + k\)
\(f(1) = a(1 - h)^2 + k\\\\6 = a(1 - h)^2 + k\)
We can use a second point to find a relationship between h and k. Let's use the point (0, 8):
\(f(0) = a(0 - h)^2 + k\\\\8 = a(-h)^2 + k\\\\6 - 8 = a(1 - h)^2 + k - (a(-h)^2 + k)\\\\-2 = a(1 - h)^2 - a(h)^2\\\\-2 = a(1 - 2h + h^2) - a(h^2)\\\\-2 = a - 2ah + ah^2 - ah^2\\\\-2 = a - 2ah\\\\a = -2/(2h - 1)\)
Let's use the second equation:
\(8 = a(-h)^2 + k\\\\8 = (-2/(2h - 1))(h^2) + k\\\\8(2h - 1) = -2h^2 + k(2h - 1)\\\\16h - 8 = -2h^2 + k(2h - 1)\\\\-2h^2 + 16h - 8 = k(2h - 1)\\\\k = (-2h^2 + 16h - 8)/(2h - 1)\)
Now we can substitute this value of h into our expressions for a and k to get:
\(a = -2/(2(0.5) - 1) = -2\\\\k = (-2(0.5)^2 + 16(0.5) - 8)/(2(0.5) - 1) = 6\)
So the equation of the quadratic function is:
\(f(x) = -2(x - 0.5)^2 + 6\)
Therefore, \(f(x) = -2(x - 0.5)^2 + 6\) is the equation of the quadratic function that passes through the points (-1, 14), (0, 8), (1, 6), and (2, 8).
To know more about quadratic function visit,
https://brainly.com/question/25841119
#SPJ1
Find f.
f '(t) = sec(t)(sec(t) + tan(t)), − π /2 < t < π /2 , f π 4 = −6
f(t) =
Answers
To find f, we need to integrate f '(t) with respect to t. Using the formula ∫sec(t)dt = ln|sec(t) + tan(t)| + C, we can rewrite f '(t) as:
f '(t) = sec(t)(sec(t) + tan(t)) = sec(t)sec(t) + sec(t)tan(t)
= sec^2(t) + sec(t)tan(t)
Now we can integrate:
∫f '(t)dt = ∫sec^2(t)dt + ∫sec(t)tan(t)dt
Using the formula ∫sec^2(t)dt = tan(t) + C, we get:
∫sec^2(t)dt = tan(t)
For the second integral, we can use u-substitution with u = sec(t), du/dt = sec(t)tan(t), so:
∫sec(t)tan(t)dt = ∫u du = 1/2 u^2 + C
= 1/2 sec^2(t) + C
Putting it all together:
f(t) = ∫f '(t)dt = tan(t) + 1/2 sec^2(t) + C
To find C, we can use the initial condition f(π/4) = -6:
-6 = tan(π/4) + 1/2 sec^2(π/4) + C
-6 = 1 + 1/2(2) + C
C = -10
Therefore, the solution is:
f(t) = tan(t) + 1/2 sec^2(t) - 10
Learn more about integrate here:
https://brainly.com/question/18125359
#SPJ11
What is the answer I need help!

Answers
Answer:
B
Step-by-step explanation:
y³=64
\(y=(64)^{\frac{1}{3} } =\sqrt[3]{64} \)
Answer:
B and F
Step-by-step explanation:
If we solve the equation \(y^3=64\), we get \(y=\sqrt[3]{64} \). Therefore, B and F are the only correct answers since \(4^3=64\) and \(\sqrt[3]{64}=4 \)
How do you Simplify 10-(-2)
Answers
Mr. Edwards purchased 3 bags of potatoes. He bought 36 potatoes in all. Each bag contains the same number of potatoes. How many potatoes are in each bag?
Answers
Answer:
12
Step-by-step explanation:
36 divided by 3 = 12
Hope This Helps
Answer:
39 or 12
Step-by-step explanation:
i got 39 by 36+3=39
i got 12 by 3 divided by 36= 12
Estimate the diameter of the cylindrical swimming pool that uses one-half of the amount of vinyl liner used to cover the larger pool. Round your answer to the nearest whole number. Assume the height of the pool is 4 feet.
Answers
The volume of the cylinder is the amount of vinyl liner it can contain.
The diameter of the swimming pool is 4 feet.
Given that:
\(h = 4\) --- height
The volume (V) of a cylinder is:
\(V = \pi r^2 h\)
The amount of vinyl liner used for the large pool is not given. So, I will make an assumption.
Assume the amount used for the large pool is 35 cubic feet.
From the question, we understand that 1.5 of this amount is used for the new pool.
So:
\(V = 1.5 \times 35ft^3\)
\(V = 52.5ft^3\)
The volume equation becomes
\(V = \pi r^2 h\)
\(52.5 = \pi r^2 h\)
Substitute 4 for h and 3.143 for \(\pi\)
\(52.5 = 3.143 \times r^2 \times 4\)
Solve for \(r^2\)
\(r^2 = \frac{52.5}{3.143 \times 4}\)
\(r^2 = \frac{52.5}{12.572}\)
\(r^2 = 4.1759\)
Take positive square roots
\(r = 2.0435\)
Multiply both sides by 2 to calculate diameter (d)
\(2r = 2 \times 2.0435\)
\(2r = 4.087\)
Rewrite as:
\(d = 4.087\)
\(d = 4\) -- approximated
Hence, the diameter of the pool (using the assumed volume) is approximately 4 feet
Read more about volumes at:
https://brainly.com/question/3010040
y varies inversely with x if y = 7 when x =-4, find y when x = 5
Answers
Answer:
y = - \(\frac{28}{5}\)
Step-by-step explanation:
Given y varies inversely with x then the equation relating them is
y = \(\frac{k}{x}\) ← k is the constant of variation
To find k use the condition y = 7 when x = - 4, then
7 = \(\frac{k}{-4}\) ( multiply both sides by - 4 )
- 28 = k
y = \(\frac{-28}{x}\) ← equation of variation
When x = 5 , then
y = \(\frac{-28}{5}\) = - \(\frac{28}{5}\)