Answers
Answer:
20 square units
Step-by-step explanation:
Area of the parallelogram= bh
b= 5 units
h= 4 units
bh= 4×5
= 20 square units
Related Questions
HELPPPP ASAP
A robber stole some jewelry in New York, sold it for $10,000.00, and put the money in a bank account in London that earns 4% interest compounded monthly. 9 years later, he was caught and found guilty of grand theft. How much had he earned in interest by then?
Round your answer to the nearest cent.
Answers
The robber earned approximately $4,824.22 in interest over the 9-year period.
To calculate the interest earned by the robber, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount,
P is the principal amount (initial investment),
r is the interest rate (expressed as a decimal),
n is the number of times interest is compounded per year,
and t is the number of years.
In this case, the robber sold the stolen jewelry for $10,000 and deposited it in a bank account in London. The interest rate is 4% per year, compounded monthly (n = 12). The time period is 9 years (t = 9). Substituting these values into the formula, we get:
A = 10,000(1 + 0.04/12)^(12*9)
Calculating this expression, we find that A is approximately $14,824.22.
To find the interest earned, we subtract the initial principal from the final amount:
Interest earned = A - P
= $14,824.22 - $10,000.00
= $4,824.22.
For more such questions on Interest:
https://brainly.com/question/25720319
#SPJ8
In the diagram, the parallel lines are cut by transversal BC−→−.If BD−→− bisects ∠ABC and m∠3 = 80, what is m∠ABD?

Answers
The value of m ∠ABD will be;
⇒ ∠ ABD = 50°
What are Parallel lines?Parallel lines are those lines that are equidistance from each other and never intersect each other.
Given that;
In the diagram, the parallel lines are cut by transversal BC.
And, BD bisects ∠ABC and m∠3 = 80.
Now,
Since, The parallel lines are cut by transversal BC.
Hence, We get;
⇒ ∠ 3 + ∠ 2 = 180°
⇒ 80° + ∠ 2 = 180°
⇒ ∠ 2 = 180 - 80
⇒ ∠ 2 = 100
And, We have;
⇒ ∠ 2 = ∠ ABC
⇒ ∠ ABC = 100°
Since, BD bisects ∠ABC.
Hence, We get;
⇒ ∠ ABD = 100 / 2
⇒ ∠ ABD = 50°
Thus, The value of m ∠ABD = 50°
Learn more about the parallel lines visit:
https://brainly.com/question/26961508
#SPJ1
Which values of x are solutions to this equation? -1/2x^2 + 5x = 8
A) -2
B) 2
C) -8
D) -1.5
E) 11.5
F) 8
Answers
Answer:
2, 8
Step-by-step explanation:
-1/2x^2 + 5x = 8
-x^2 + 10x = 16 (Multiplying both sides of the equation by 2)
-x^2 + 10x - 16 = 0
x^2 - 10x + 16 = 0 (changing the signs)
x^2 -2x -8x +16 = 0
x (x-2) -8 (x-2) = 0
(x-2) (x-8)
x-2 = 0
x = 2
or
x -8 = 0
x = 8
Answer from Gauthmath
The values of x are solutions to this equation that is 2, 8
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
We are given that the equation as;
-1/2x² + 5x = 8
-x² + 10x = 16
Now Multiplying both sides of the equation by 2;
-x² + 10x - 16 = 0
Or
x² - 10x + 16 = 0
x² -2x -8x +16 = 0
x (x-2) -8 (x-2) = 0
(x-2) (x-8)
The solution are;
x-2 = 0
x = 2
or
x -8 = 0
x = 8
Learn more about equations here;
https://brainly.com/question/25180086
#SPJ2
Solve the system by the addition method. x + 3y = 6 3x + 4y = −2
Answers
The solution to the system is x = -6 and y = 4.
To solve the system by the addition method, we want to add the equations together in a way that will eliminate one of the variables.
Let's start by multiplying the first equation by -3 to get -3x - 9y = -18, and then add the second equation to it:
-3x - 9y = -18
+ 3x + 4y = -2
-------------
-5y = -20
Now we can solve for y by dividing both sides by -5:
y = 4
We can substitute y=4 into one of the original equations, say x+3y=6, to solve for x:
x + 3(4) = 6
x + 12 = 6
x = -6
So the solution to the system is x = -6 and y = 4.
for such more question on variables.
https://brainly.com/question/19803308
#SPJ11
Please help me i am not downloading anything
Answers
Answer:
on what
Step-by-step explanation:
A circle has the equation (x - 7)2 + (y + 6)2 = 121. Which of thefollowing statements is NOT true?O The diameter of the circle is 22.O The y coordinate of the center is 6.O The y coordinate of the center is 6.O The x coordinate of the center is 7.
Answers
A circle has the following equation
\(\mleft(x-7\mright)^2+(y+6)^2=121\)graph the function y less than or equal to x^2-3x-1
Answers
Answer: y <= x^(2) - 3x - 1
How to: Graph the inequality by finding the boundary line, then shading the appropriate area.
Have a great day and stay safe !
Claim: Fewer than 91% of adults have a cell phone. In a reputable poll of 1072 adults, 85% said that they have a cell phone. Find the value of the test statistic. (Round to two decimal places as needed.)
Answers
Answer:
911.20
Step-by-step explanation:
Adults that have a cell phone = 85% of 1072
= 0.85 x 1072
= 911.20
Find the height of the tower using the information given in the illustration.

Answers
using SOH CAH TOA
Tan 85.144 =h/130
h=tan 85.144*130
h=1530.19 fr

A moving company charges a flat rate of $150, and an additional $5 for each box. if a taxi service would charge no flat rate and $15 for each box, how many boxes would you need for it to be cheaper to use the moving company? (do not label your answer)
Answers
Answer:
16 boxes
Step-by-step explanation:
16x5=80+150=230>15x16=240
which of the following is equivalent to x^2 -5x +6
Answers
Hello!
x² - 5x + 6
= (x² - 2x) + (-3x + 6)
= x(x - 2) - 3(x - 2)
= (x - 2)(x - 3)
write an equation in slope intercept form that passes through the given point and is perpendicular to the graph of given equation (1,-2) y=5x+4
Answers
The equation of the line perpendicular to y = 5x + 4, passing through the point (1, -2), is y = (-1/5)x - 9/5.
To find an equation in slope-intercept form that passes through the point (1, -2) and is perpendicular to the given equation y = 5x + 4, we need to determine the slope of the perpendicular line.
The given equation y = 5x + 4 is already in slope-intercept form (y = mx + b), where m represents the slope. In this case, the slope of the given line is 5.
To find the slope of a line perpendicular to this, we use the fact that the product of the slopes of two perpendicular lines is -1. So, the slope of the perpendicular line can be found by taking the negative reciprocal of the slope of the given line.
The negative reciprocal of 5 is -1/5.
Now that we have the slope (-1/5) and a point (1, -2), we can use the point-slope form of the equation:
y - y1 = m(x - x1)
Substituting the values:
y - (-2) = (-1/5)(x - 1)
Simplifying:
y + 2 = (-1/5)(x - 1)
To convert the equation into slope-intercept form (y = mx + b), we need to simplify it further:
y + 2 = (-1/5)x + 1/5
Subtracting 2 from both sides:
y = (-1/5)x + 1/5 - 2
Combining the constants:
y = (-1/5)x - 9/5
Therefore, the equation of the line perpendicular to y = 5x + 4, passing through the point (1, -2), is y = (-1/5)x - 9/5.
For more question on perpendicular visit:
https://brainly.com/question/1202004
#SPJ8
Select the correct answer. The square of z varies inversely as the square root of e. If z=36 when w=16, what is the value of z when w=81?
a. 54
b. 24
c. 182 1/4
d. 7 1/9
Answers
The square of z varies inversely as the square root of e. If z=36 when w=16, then value of z is 24 when w=81.
What is Ratio?A ratio is an ordered pair of numbers a and b, written a / b where b does not equal 0.
The square of z varies inversely as the square root of e.
If z=36 when w=16
The value of z when w is 81 we need to find
z²=k/√e
where k is a proportionality constant
36²=k/√16
36²=k/4
Apply cross multiplication
1296(4)=k
5184=k
Now let us find when k is 5184 and w is 81
z²=5184/9
z²=576
Take square root on both sides
z=24
Hence, the value of z is 24 when w is 81.
To learn more on Ratios click:
https://brainly.com/question/13419413
#SPJ2
Please awnser asap I will brainlist
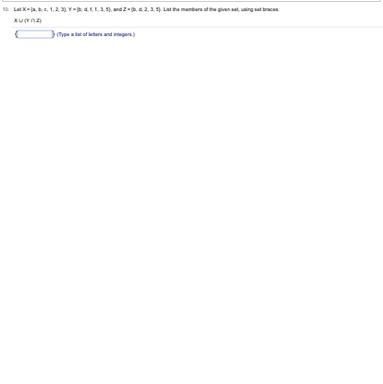
Answers
The members of the given set in this problem are given as follows:
X U (Y ∩ Z) = {p, q, r, 0, 6, 21, 22, 23, 26}
How to obtain the union and intersection set of two sets?The union and intersection sets of multiple sets are defined as follows:
The union set is composed by the elements that belong to at least one of the sets.The intersection set is composed by the elements that belong to at all the sets.The intersection of the sets Y and Z for this problem is given as follows:
Y ∩ Z = {0, 6, 23, 26}
(which are the elements that belong to both of the sets).
The union of the above set with the set X is given as follows:
X U (Y ∩ Z) = {p, q, r, 0, 6, 21, 22, 23, 26}
(elements that belong to at least one of the sets).
More can be learned about union and intersection at brainly.com/question/4699996
#SPJ1
A residential community was polling households to find out whether they wanted to get their TV signal from a satellite or cable. The results are shown in the Venn diagram.
A circle labeled satellite 55 overlaps a circle labeled cable 75. Overlap is labeled 12. 4-column table with 3 rows. First column has no label with entries satellite, not satellite, total. Second column is cable with entries blank, 51%, blank. Third column is not cable with entries a, b, blank. Fourth column is labeled total with entries blank, blank, 100%.
What are the values of a and b in the relative frequency table for the survey results? Round answers to the nearest percent.
a = 82%, b = 3%
a = 38%, b = 50%
a = 38%, b = 3%
a = 93%, b = 19
Answers
The correct answer is:
a = 43%
b = 88%
To determine the values of a and b in the relative frequency table, we need to analyze the information provided in the Venn diagram and the given table.
From the Venn diagram, we can gather the following information:
The circle labeled "satellite" has a value of 55.
The circle labeled "cable" has a value of 75.
The overlap between the two circles is labeled as 12.
Using this information, we can complete the table:
First column - "Satellite":
Entries: Satellite, Not satellite, Total
Total: 55 (as given in the Venn diagram)
Second column - "Cable":
Entries: Blank, 51%, Blank
To find the value for the "Cable" entry, we need to subtract the overlap (12) from the total number of cable users (75).
Cable: 75 - 12 = 63
Therefore, the entry becomes: Blank, 51%, Blank
Third column - "Not Cable":
Entries: a, b, Blank
To find the value for "a," we subtract the overlap (12) from the total number of satellite users (55).
a: 55 - 12 = 43
To find the value for "b," we subtract the overlap (12) from the total number of households (100).
b: 100 - 12 = 88
Therefore, the entries become: 43, 88, Blank
Fourth column - "Total":
Entries: Blank, Blank, 100%
The total number of households is given as 100% (as stated in the question).
Therefore, the values of a and b in the relative frequency table are:
a = 43% (rounded to the nearest percent)
b = 88% (rounded to the nearest percent)
Hence, the correct answer is:
a = 43%
b = 88%
for such more question on values
https://brainly.com/question/27746495
#SPJ8
What is the unit rate if you drove a go-kart 9 miles in 36 minutes?
Answers
Answer:
Step-by-step explanation:
To find the unit rate, we need to divide the distance traveled by the time taken.
In this case, the distance traveled is 9 miles, and the time taken is 36 minutes.
Unit rate = distance/time
Unit rate = 9 miles / 36 minutes
Simplifying the above expression by dividing both numerator and denominator by 9, we get:
Unit rate = 1 mile / 4 minutes
Therefore, the unit rate at which the go-kart is traveling is 1 mile per 4 minutes.
Use the ray tool to graph f(x) = |-x – 5|.
First plot the endpoint of the ray, then any point on the ray.
Answers
The graph of the given absolute function is attached below and the end points (-5,0) (0, 5) of the rays are marked in it.
Absolute value function:
The function that contains an algebraic expression within absolute value symbols is called as absolute value function.
Given,
Here we have the absolute value function f(x) = |-x - 5|
Now, we have to plot the graph for this function and we have to mark the end point of the rays.
Here the given function is written as,
=> f(x) = | -x - 5|
In order to plot the graph for the function we need the table of values to point it on the graph,
For that we have to take following sample values,
When x = -5, then f(-5) = |-5 -5| = 0
When x = 0, then f(0) = |0 - 5| = 5
Therefore, the end points of the rays are (-5,0) and (0,5)
Now, we have to plot these values on the graph.
Then we get the graph like the following.
To know more about Absolute value function here.
https://brainly.com/question/10664936
#SPJ1

How much time, in seconds, did the vehicle in this diagram spend STOPPED?

Answers
Answer:
like 10 i think
Step-by-step explanation:
the flat line is the time it spends stopped im pretty sure so that would be 10 seconds
through: (0, 3) and (-4, -1)
Answers
Answer:
\(m = 1\) -- Slope
\(y = x + 3\) --- Equation
Step-by-step explanation:
Given
\((x_1,y_1) = (0,3)\)
\((x_2,y_2) = (-4,-1)\)
Required
The slope and the equation
The slope (m) is calculated using:
\(m=\frac{y_2 - y_1}{x_2 - x_1}\)
\(m=\frac{-1-3}{-4- 0}\)
\(m=\frac{-4}{-4}\)
\(m = 1\)
The equation is calculated using:
\(y = m(x - x_1) + y_1\)
This gives:
\(y = 1(x - 0) + 3\)
\(y = 1(x) + 3\)
\(y = x + 3\)
ANSWER THE QUESTION FOR BRAINLIEST

Answers
In Exercises 5-8, use the graph which shows the right-hand and left-hand behavior of a polynomial function f.
Answers
The other information required while using the intermediate value theorem to show the existence of zero for the polynomial function plotted is
f(x₁) < 0 and f(x₂) > 0
What is intermediate value theorem?The intermediate value theorem says that if "f" is a continuous function across a closed interval [a, b] with values f(a) and f(b) at its endpoints, then the function takes any value at a point inside the interval that is between the values of f(a) and f(b).
The root of a polynomial is the value of y when x is zero. hence to show that there is a zero between the points x₁ and x₂ there is a need to show there was a change of sign in the output value
Using the graph
f(x₁) is less than 0 which shows negative values f(x₂) is greater than 0 which shows positive valuesAt the point of change of sign is the required zero
Learn more about intermediate value theorem at:
https://brainly.com/question/21793689
#SPJ1

Which pair of expressions are equivalent?
A
3x+2+2x and 7x
B
8(x−3) a
nd 8x−24
C
4(x+1) and 4x+1
D
3(5x) and 8x
Answers
if it is given that "x" is 23.5 - proof that it is a point of intersection at y= 1/2(x) - 25 if y is equal to 11. been trying but not working out.
Answers
When substituting y = 11 into the equation y = 1/2(x) - 25, we find that x = 72, confirming that (23.5, 11) is a valid point of intersection.
Given that x is 23.5, it is required to prove that it is an intersection point for the equation y = 1/2(x) - 25 when y is equal to 11.
The equation is given as y = 1/2(x) - 25
When y = 11, we can substitute the value of y in the equation to obtain 11 = 1/2(x) - 25
This can be simplified as 11 + 25 = 1/2(x)36 = 1/2(x)
On solving, x = 72Thus, when y is equal to 11 and x is equal to 72, the given point of intersection is valid.
Therefore, it can be concluded that x = 23.5 is a point of intersection for the equation y = 1/2(x) - 25 when y is equal to 11.
In summary, when given an equation with two variables, we can find the point of intersection by setting one of the variables to a given value and solving for the other variable. In this case, when y is equal to 11, we can solve for x and obtain the point of intersection as (72,11).
For more questions on intersection
https://brainly.com/question/30429663
#SPJ8
Let D = D(R), where Þ(u, v) = (u², u + v) and
R = [1, 8] × [0, 6].
Calculate
y dA.
Note: It is not necessary to describe D.
Joyda
=
![Let D = D(R), where (u, v) = (u, u + v) andR = [1, 8] [0, 6].Calculatey dA.Note: It is not necessary](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/kXU0XdQfL262QE4gZDOxcOqjtmzz7YTd.png)
Answers
The region \(D\) is essentially parameterized in three dimensions by
\(\Phi(u,v) = (u^2, u+v, 0)\)
with \(1\le u\le8\) and \(0\le v\le6\).
The normal vector to \(D\) is
\(\vec n = \dfrac{\partial\Phi}{\partial u} \times \dfrac{\partial\Phi}{\partial v} = (0,0,2u)\)
with norm \(\|\vec n\| = 2u\).
Then the surface integral is
\(\displaystyle \iint_D y \, dA = 2 \int_0^6 \int_1^8 (u+v)u \, du \, dv \\\\ = 2 \int_0^6 \left(\frac{1022}3 + 63 v\right) \, dv = \boxed{3178}\)
1 a tobacco company produces blends of tobacco, with each blend containing various proportions of turkish, domestic, and other tobaccos. the proportions of turkish and domestic in a blend are random variables with joint density function (x
Answers
(a) 0.5, (b) f_Y(y) = 12y(1-y), (c) 9/128, (d) 7/36 - Probability calculations using joint density function.
(a) To find the Probability that the Turkish tobacco represents over a portion of the mix, we want to incorporate the joint thickness capability over the district where x > 0.5 and y < 1 - x. This gives:
P(X > 0.5) = ∫[0.5,1]∫[0,1-x] 24xy dy dx = 0.5
Consequently, the Probability that the Turkish tobacco represents over around 50% of the mix is 0.5.
(b) To find the negligible thickness capability for the extent of homegrown tobacco, we really want to incorporate the joint thickness capability over all potential upsides of Turkish tobacco:
f_Y(y) = ∫[0,1-y] 24xy dx = 12y(1-y) ; 0 < y < 1
Thusly, the peripheral thickness capability for the extent of homegrown tobacco is f_Y(y) = 12y(1-y).
(c) To find the Probability that the extent of Turkish tobacco is under 1/8 given that the mix contains 3/4 homegrown tobacco, we really want to utilize Bayes' standard:
P(X < 1/8 | Y = 3/4) = P(X < 1/8 ∩ Y = 3/4)/P(Y = 3/4)
We can find the numerator by coordinating the joint thickness capability over the district where x < 1/8 and y = 3/4:
∫[0,1/8] 24xy dx = 27/128
To find the denominator, we coordinate the joint thickness capability over all potential upsides of Turkish tobacco when y = 3/4:
∫[0,1/4] 24xy dx = 3
Thusly, the contingent Probability is:
P(X < 1/8 | Y = 3/4) = (27/128)/3 = 9/128
(d) To find the likelihood that the extent of homegrown tobacco is over two times the extent of the Turkish tobacco, we want to incorporate the joint thickness capability over the area where y > 2x and x + y < 1. This gives:
P(Y > 2X) = ∫[0,1/3]∫[2x,1-x] 24xy dy dx + ∫[1/3,1/2]∫[2x,1-x] 24xy dy dx
= 7/36
Accordingly, the likelihood that the extent of homegrown tobacco is over two times the extent of the Turkish tobacco is 7/36
To learn more about marginal density function and probability, refer:
https://brainly.com/question/15109814
#SPJ4
The complete question is:
A tobacco company produces blends of tobacco, with each blend containing various proportions of Turkish, domestic, and other tobaccos. The proportions of Turkish and domestic in a blend are random variables with joint density function (X = Turkish and Y = domestic) 24xy ;0< x, y < 1, x +y<1 fx.y(1,7) (2) ; otherwise (a) (1 point) Find the probability that in a given box the Turkish tobacco accounts for over half the blend. Page 2 (b) (1 point) Find the marginal density function for the proportion of the domestic tobacco. (c) (1 point) Find the probability that the proportion of Turkish tobacco is less than 1/8 if it is known that the blend contains 3/4 domestic tobacco. (d) (2 points) Find the probability that the proportion of domestic tobacco is more than twice the proportion of the Turkish tobacco.
Please answer these 3 questions

Answers
The Volume of the box is 12 cubic unit.
We have,
Height = 1 unit
Width = 2 unit
Length = 6 unit
So, Volume of box
= l w h
= 1 x 2 x 6
= 12 cubic unit
Learn more about Volume here:
https://brainly.com/question/13338592
#SPJ1
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
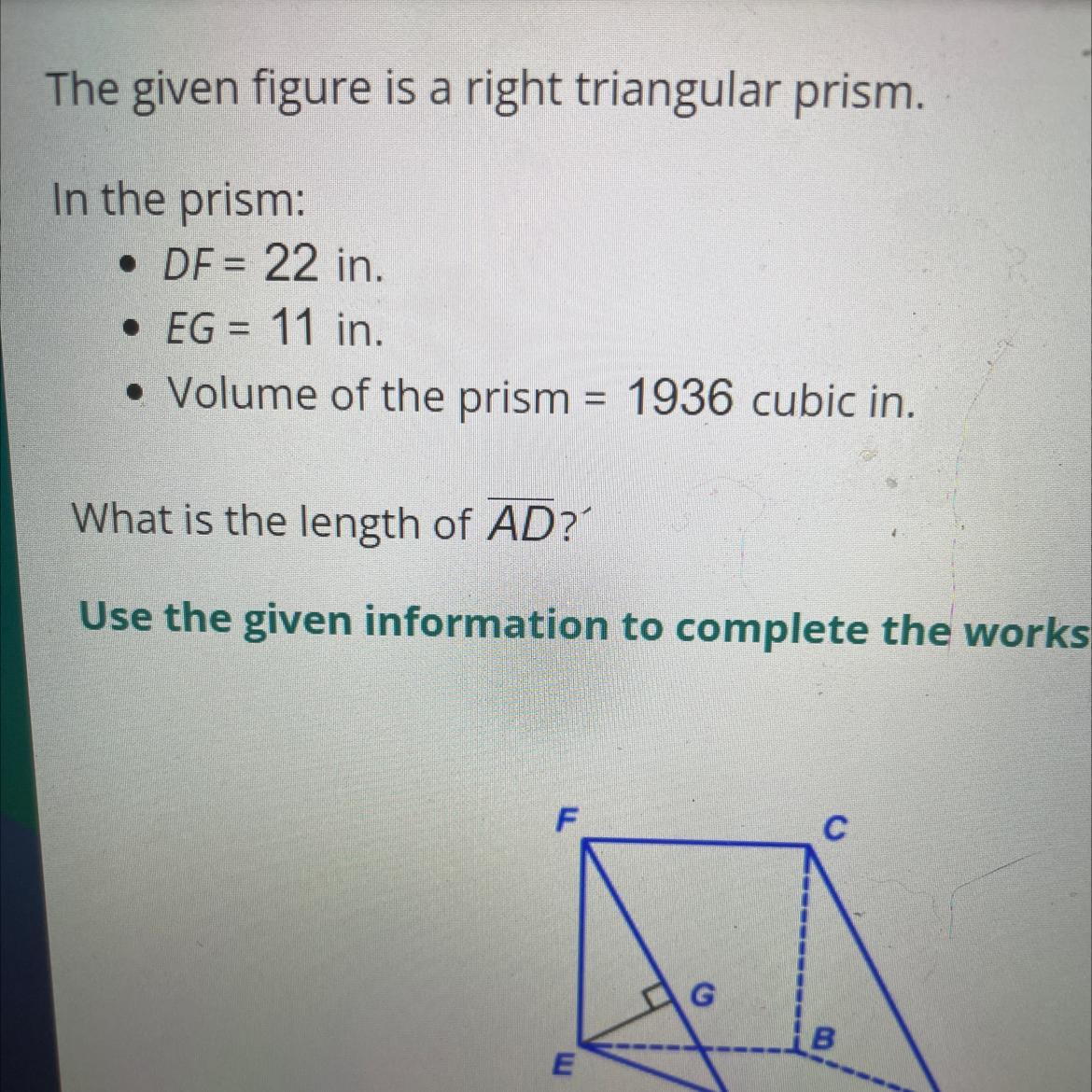
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Find the constant term in the expansion of (2x+1/x)8
Answers
Answer:
the constant term in this problem is 8
For all x≠±y , x/(x+y)+y/(x−y)= ?
Answers
The value of the equation is A = ( x² + y² ) / ( x² - y² )
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Substituting the values in the equation , we get
A = x / ( x + y ) + y / ( x - y )
On simplifying the equation , we get
Multiply by the LCM , we get
x / ( x + y ) + y / ( x - y ) = [ x ( x - y ) + y ( x + y ) ] / ( x + y ) ( x - y )
where the denominator ( x + y ) ( x - y ) = ( x² - y² )
Substituting the values in the equation , we get
x / ( x + y ) + y / ( x - y ) = [ x² - xy + xy + y² ] / ( x² - y² )
On further simplification , we get
A = ( x² + y² ) / ( x² - y² )
Hence , the equation is A = ( x² + y² ) / ( x² - y² )
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Please solve the missing parts

Answers
Answer:
34 28 37 56 34 37 28 20 43 15
