Answers
Answer:
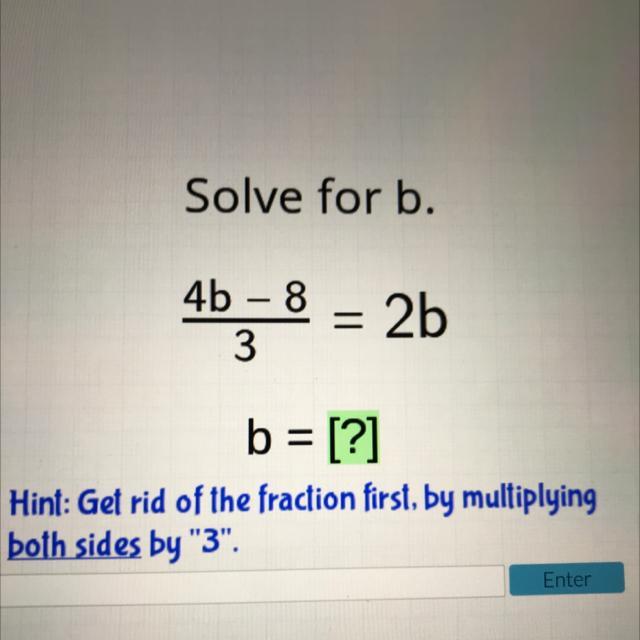
.3 repeating
Step-by-step explanation:
Answer:
b=-4/21
Step-by-step explanation:
Related Questions
Find the critical point(s) of the function. (x,y)=6^(x2−y2+4y) critical points: compute the discriminant D(x,y) D(x,y):
Answers
The critical point of the function is (0, 2). The discriminant D(x,y) to be -256*(2-y)^3*6^(2(x+2y)).
The function is given as (x,y) = 6^(x2−y2+4y) and we are required to find the critical points of the function.
We will have to find the partial derivatives of the function with respect to x and y respectively.
We will then have to equate the partial derivatives to zero and solve for x and y to obtain the critical points of the function.
Partial derivative of the function with respect to x:
∂/(∂x) (x,y) = ∂/(∂x) 6^(x2−y2+4y) = 6^(x2−y2+4y) * 2xln6... (1)
Partial derivative of the function with respect to y
:∂/(∂y) (x,y) = ∂/(∂y) 6^(x2−y2+4y) = 6^(x2−y2+4y) * (-2y+4)... (2)
Now, equating the partial derivatives to zero and solving for x and y:
(1) => 6^(x2−y2+4y) * 2xln6 = 0=> 2xln6 = 0=> x = 0(2) => 6^(x2−y2+4y) * (-2y+4) = 0
=> -2y + 4 = 0
=> y = 2
Therefore, the critical point of the function is (0, 2).
Next, we will compute the discriminant D(x, y):
D(x, y) = f_{xx}(x, y)f_{yy}(x, y) - [f_{xy}(x, y)]^2 = [6^(x2−y2+4y) * 4ln6][6^(x2−y2+4y) * (-2) + 6^(x2−y2+4y)^2 * 16] - [6^(x2−y2+4y) * 4ln6 * (-2y+4)]^2= -256*(2-y)^3*6^(2(x+2y))
Hence, the discriminant D(x,y) to be -256*(2-y)^3*6^(2(x+2y)).
Learn more about discriminant here:
https://brainly.com/question/32434258
#SPJ11
when to use the one mean Z test for small samples of size less than 15
Answers
The one mean Z test can be used for small samples of size less than 15 when the population standard deviation is known.
The one-mean z-test is a hypothesis test that is used to test a hypothesis about the mean of a population when the population standard deviation is known, and the sample size is large (typically greater than 30).
When the sample size is small (less than 15), the one-mean z-test is not appropriate because the assumptions of the test may not be met.
When the sample size is small, we typically use a t-test instead of a z-test to test a hypothesis about the population mean.
Specifically, we use a one-sample t-test when the population standard deviation is unknown, and the sample size is small (typically less than 30).
The one-sample t-test uses a t-distribution to calculate the p-value and test the null hypothesis about the population mean.
It is important to note that the sample size of 15 is not a hard and fast rule for when to switch from the z-test to the t-test.
The decision of which test to use depends on the specific context and the assumptions of the test.
In general, if the population standard deviation is unknown and the sample size is small (less than 30), then we use the t-test. If the population standard deviation is known and the sample size is large (greater than 30), then we use the z-test.
For similar question on Z test:
https://brainly.com/question/15683598
#SPJ11
the study of hypnosis and its relationship to hysteria was the starting point for
Answers
The study of hypnosis and its relationship to hysteria was the starting point for the development of psychoanalysis by Sigmund Freud.
The study of hypnosis and hysteria in the late 19th century by Sigmund Freud and his contemporaries led to the development of psychoanalysis, a form of psychotherapy that emphasizes the role of unconscious thoughts and feelings in shaping behavior. Through his work with patients suffering from hysteria, Freud became interested in the idea that psychological conflicts could be traced back to early childhood experiences, and that these conflicts could be resolved through the exploration of unconscious thoughts and feelings. This eventually led to the development of psychoanalysis as a theory and practice for the treatment of psychological disorders.
To know more about hypnosis,
https://brainly.com/question/14375336
#SPJ11
I NEED HELP ASAP
Write the slope-intercept form of the equation with the given characteristics: Slope: 3/2 Point: (-4,7)
Answers
Answer:
\(y = \frac{3}{2} x + 13\)
Step-by-step explanation:
1) Use point-slope formula \(y-y_1 = m (x-x_1)\) to find the slope-intercept form (or y = mx + b form) of the equation. m represents the slope, and \(x_1\) and \(y_1\) represent the x and y values of a point the line intersects. So, substitute \(\frac{3}{2}\) for m, -4 for \(x_1\), and 7 for \(y_1\). Then, simplify and isolate y on the left side like so:
\(y-(7) = \frac{3}{2} (x - (-4)) \\y -7 = \frac{3}{2} (x + 4) \\y - 7 = \frac{3}{2} x + 6\\y = \frac{3}{2} x + 13\)
.The seventh grade math classes are going on a field trip. The field trip will cost $5 per student. Write an expression to find the cost of the field trip for s students. What is the total cost if 25 students go on the trip?
Answers
Answer:
5 x S = M (S=Students, M = money); 5 x 25 = 100
y= 3x + a / 2x -5
express x in terms of a and y
Answers
The equation y = 3x +a / 2x - 5 can be expressed in terms of a and y as x = (a - 5y) / (2y-3)
Given equation y = 3x + a / 2x - 5
= y(2x - 5) = 3x + a
= 2xy - 5y = 3x + a
= 2xy - 3x = a - 5y
= x(2y-3) = a - 5y
Hence, x = (a - 5y) / (2y - 3)
First, we will move the denominator 2x-5 and multiply it by y giving us 2xy-5y. Next, we will move all the terms which contain only a and y to one side and the rest remaining to another side, giving us 2xy - 3x = a - 5y. Since we need to express the equation in terms of x we take it as common from left-hand side of the equation and the remaining part we move to the right-hand side as the denominator. Hence we get our equation in terms of a and y as x = (a - 5y) / (2y - 3).
To learn more about polynomial equations,
https://brainly.com/question/20121808
Need help really fast pleasessssssssssss

Answers
Answer:
1/2x plus 1/3
Step-by-step explanation:
Answer:
the guy above me is correct
Step-by-step explanation:
A manufacturer sent free boxes of tissue to 100 random homes in Miami at the beginning of January. At the end of January, a representative found an average of 3 boxes of tissues had been used in each home. The representative concluded that the average home in the United States uses 36 boxes of tissue per year. Is his conclusion correct
Answers
Answer:
conclusion of representative is incorrect
Step-by-step explanation:
The total random samples of 200 homes in Miami uses 3 boxes of tissues per home.
This is true only for Miami. Miami's population is not the correct representation of the population of USA.
Also, there are several other factors such as population group residing in Miami, their education level, heath etc. plays a major role as a variable. These variables in case of USA will be entirely different.
Hence, conclusion of representative is incorrect
a necklace is made from 164 purple and blue beads. there are 8 more purple beads and blue beads how many of each colour bead are there.
Answers
Answer:74 blue beads and 90 purple beads
Step-by-step explanation:
first you need to take the total number of beads 164 divide by the 2 colors so 164÷2=86 then you subtract the 8 more purple from 1/2 of 86 and you get 74 then you add 8 more to the other half of 82 and get 90 purple and 74 blue.
can someone please help me find the slope on khan academy? and please provide an explanation if possible

Answers
Answer: 7/4
Step-by-step explanation: To find the slope of a line, pick any two integer points, in this scenario the only two are (3,4) and (-1,-3). The slope is the rise over run, so think about it. To get from (-1,-3) to )3,4) you need to rise 7 units (difference in y coordinates) and from there you need to run 4 units, so it is 7/4. Keep in mind that rising up is positive for y and running to the right is positive for x.
Answer:
\(\frac{7}{4}x\)
Step-by-step explanation:
How do you find slope on a graph? The slope is "rise/run" where "rise" is how much y spaces are moved to the next point and "run" is the how much spaces are moved to the next x point.
Step One: In this case, the point moves up 7 spaces to the next point, so that's the "rise" and then it moves 4 spaces to the right to the next point, so that's the "run"
Step Two: When we put it together, it is 7/4x. The x is just an indication that this is slope, and you don't have to worry about it until you learn how to plug it in.
20 applicants from a pool of 90 applications will be hired. How many ways are there to select the applicants who will be hired?
Answers
The ways are the \(C_{20} ^{90}\) which are we there to select the applicants who will be hired with the help of combination.
According to the statement
we have to find that the number of ways are there to select the applicants who will be hired.
So, For this purpose, we know that the
A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter.
Here we use the combination.
And from the given information:
20 applicants from a pool of 90 applications will be hired.
And according to this the combination becomes:
\(C_{20} ^{90}\)
then solve it
\(C_{20} ^{90} = \frac{90!}{20! (70!)}\)
\(C_{20} ^{90} = \frac{90*89*88*87*86*85*84*83*82!}{20*19*18*17*16*15*14!}\)
Then after solve it
\(C_{20} ^{90} = \frac{89*11*87*43*14*83*82!}{19*14!}\)
Now open another factorial
\(C_{20} ^{90} = \frac{89*11*87*43*14*83*82*81*80*79*78*77*76*75*74*73*72*71}{19*14*13*12*11*10*9*8*7*6*5*4*3*2*1}\)
Now solve this then
\(C_{20} ^{90} = {89*11*87*43*83*82*79*15*74*73*71}\).
So, The ways are the \(C_{20} ^{90}\) which are we there to select the applicants who will be hired with the help of combination.
Learn more about combination here
https://brainly.com/question/11732255
#SPJ4
Suppose the total benefit derived from a given decision, Q is B(Q)=40Q−2Q^2 , and the corresponding total cost is C(Q)=4+2Q^2. What level of Q will yield the maximum net benefits? How much is the maximum level of benefits? o 4,96 o 4. 92 o 5,92 o 5,96
Answers
The level of Q that will yield the maximum net benefits is 4.92, and the maximum level of benefits is 96.
To find the level of Q that maximizes net benefits, we need to calculate the difference between the total benefits (B(Q)) and the total costs (C(Q)). In this case, the net benefits (NB) can be represented as NB(Q) = B(Q) - C(Q).Given B(Q) = 40Q - 2\(Q^2\) and C(Q) = 4 + 2\(Q^2\), we can substitute these expressions into the net benefits equation:
NB(Q) = (40Q - 2\(Q^2\)) - (4 + 2\(Q^2\))
Simplifying, we get:
NB(Q) = 40Q - 2\(Q^2\) - 4 - 2\(Q^2\)
NB(Q) = -4\(Q^2\) + 40Q - 4
To find the level of Q that maximizes net benefits, we need to find the value of Q that maximizes NB(Q). This can be done by finding the maximum point of the quadratic function. In this case, the maximum point occurs at the vertex of the quadratic.
The formula for the x-coordinate of the vertex of a quadratic function of the form a\(x^2\) + bx + c is given by x = -b / (2a). In our case, a = -4 and b = 40.
Calculating the x-coordinate of the vertex:
Q = -40 / (2 * -4)
Q = 40 / 8
Q = 5
Therefore, the level of Q that yields the maximum net benefits is Q = 5. Plugging this value back into the net benefits equation, we can calculate the maximum level of benefits:
NB(5) = -4\((5)^2\) + 40(5) - 4
NB(5) = -4(25) + 200 - 4
NB(5) = -100 + 200 - 4
NB(5) = 96
Hence, the maximum level of benefits is 96.
Learn more about quadratic function here:
https://brainly.com/question/18958913
#SPJ11
Rick and Jon start walking from the same location. Rick starts 15 seconds before Jon and walks at a rate of 3 feet per second. Jon walks at a rate of 4 feet per second in the same direction as Rick. Which equation could you solve to find how long it will take Jon to catch up with Rick?
Answers
Answer:
hfjf fnnc v jud dbhj ejem emd jfbf
Step-by-step explanation:
Which expression is equivalent to (60)2 – (12)?? (60 – 12)
(60 - 12) (60 - 12)
(60 + 12)(60 – 12)
(60 + 12)
Answers
Answer:(60 + 12)(60 – 12)
Step-by-step explanation:
Your teacher asked your class to describe a real world situation in which a y-intercept is 100 and the slope is 5. Your partner gave the following description: My younger brother originally had 100 small building blocks, but he has lost 5 of them every month since. What mistake did your partner make?
Answers
Answer:
He should have said that his small brother had 100 small building bricks, but lost 5 in total now.
A survey was given to a random sample of 400 residents of a town to determine whether they support a new plan to raise taxes in order to increase education spending. Of those surveyed, 168 respondents said they were in favor of the plan. Determine a 95% confidence interval for the proportion of people who favor the tax plan, rounding values to the nearest thousandth.
Answers
The standard error of the sample proportion is sqrt[(0.42)(0.58)/400] = 0.032.
Using a 95% confidence level, the critical value is 1.96.
The margin of error is 1.96 * 0.032 = 0.063.
The 95% confidence interval is 0.42 ± 0.063, which is (0.357, 0.483).
Therefore, we can be 95% confident that the true proportion of people who favor the tax plan is between 0.357 and 0.483.
Question content area top
Part 1
Write an equivalent expression without parentheses. Then simplify the result.
m−(8−3m)
Answers
using exponents, On simplifying the equation, we get =4m+8.
The PEMDAS order of operations must be followed when you want to simplify a mathematical equation without using parenthesis (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). There are no parenthesis in the expression, so you may start looking for exponents. If it does, first make that simpler.
What is the main objective of simplification?Work simplification is to develop better work processes that boost output while cutting waste and costs.
What does simplifying mean in algebra?Simplifying an expression is the same as solving a mathematical issue. When you simplify an equation, you essentially try to write it as simply as you can. There shouldn't be any more multiplication, dividing, adding, or deleting to be done when the process is finished.
Given equation,
m-(8-3m)
=m-8+3m
=4m+8
To know more about exponents visit:-
brainly.com/question/11709654
#SPJ1
what is the quotient of the expression
\( \frac{21a {}^{3} b - 14ab {}^{2} + 7ab}{7ab} \)
Answers
A car dealership has been keeping detailed records of the colors of
cars sold during the current year. This chart shows the probabilities
for each color.
Colors of Cars Sold
silver = 23% white = 18% black = 15% other = 44%
What is the probability that a customer will purchase a silver or white car?
Answers
Answer:
41% or 41/100
Step-by-step explanation:
Since percentage (%) means out of 100 using fractions would be the easiest
18/100 + 23/100 = 41/100 or 41%
41/100 is non-reducible.
to check you did the right math, all percentages should equal 100
44/100 + 15/100 = 59/100
59/100 + 41/100 = 100/100
your answer is 41% or 41/100
hope this helps:)
Solve: (a + 11)9
plz help ill give the first person brainliest i need it in 10 minutes
Answers
Answer:
See below
Step-by-step explanation:
(a+11)9
a*9=9a
11*9=99
a+11 is the simplified version.
-hope it helps
Solve 2(x+3)=-4(x + 1) for x.
Answers
Answer:
The answer is x = \(\frac{-5}{3}\).
Step-by-step explanation:
First, we expand the brackets. Therefore:
\(2x+6 = -4x+(-4)\)
\(2x+6 = -4x -4\)
Then, we separate the like terms:
\(2x+4x = -4-6\)
Then we add the like terms up and solve for x:
\(6x = -10\)
Therefore:
\(x = \frac{-10}{6}\)
which, simplified, is:
\(x = \frac{-5}{3}\).
7.50x30 help i hate math
Answers
Answer:
225
Step-by-step explanation:
Answer:
225
Step-by-step explanation:
7.50 times 30 = 225
The Blue Shell's flight path is modeled by the equation:
y = -10x2 + 100x + 750
a) Fill in the table below. The points will be used to plot on the below graph to create a
parabola.
b) Based on the table, what is the maximum
Y у
height the blue shell reaches?

Answers
Answer:
1. I assume you just pick some arbitrary x and y numbers to plug in the equation. but if you answer part b and c first, part a might be easier for what values to choose.
2. if you do a quick browser search for how to find the max height of a parabola, then you can learn how to.
3. research on Browser. you can also just make y = 0.
vertex is max height, both zeros is just solving the equation for the x values. axis of symmetry is just the vertex point with a line through it.
For the demand function q=D(p)= (p+2) 2
500
, find the following. a) The elasticity b) The elasticity at p=9, stating whether the demand is elastic, inelastic or has unit elasticity c) The value(s) of p for which total revenue is a maximum (assume that p is in dollars) a) Find the equation for elasticity. E(p)= b) Find the elasticity at the given price, stating whether the demand is elastic, inelastic or has unit E(9)= (Simplify your answer. Type an integer or a fraction.) Is the demand elastic, inelastic, or does it have unit elasticity? A. elastic B. inelastic C. unit elasticity c) The value(s) of for which total revenue is a maximum (assume that is in dollars). $ (Round to the nearest cent as needed. Use a comma to separate answers as needed.)
Answers
a) The equation for the elasticity is\(\frac{1000p}{p^2 + 4p + 4}\).
b) The elasticity at p = 9 is approximately 74.38, indicating elastic demand.
c)\(\frac{d(TR) }{dp } =\frac{3p^2 + 8p + 4}{500 }\)the value(s) of p for which total revenue is a maximum.
a) To find the elasticity of the demand function, we use the formula:
E(p) =\(\frac{ p }{q}\)* (\(\frac{dq }{dp}\))
where p is the price and q is the quantity demanded.
Given the demand function q = D(p) = \(\frac{(p + 2)^2}{ 500}\), we can find the derivative of q with respect to p:
\(\frac{dq }{dp}\) = \(\frac{2(p + 2) }{ 500}\)
Now we can substitute the values into the elasticity formula:
E(p) =\(\frac{ p }{q}\)* (dq / dp)
= (\(\frac{p }{\frac{((p + 2)^2 )}{500} }\)) * \(\frac{2(p + 2) }{ 500}\)
= \(\frac{(p * 2(p + 2)) }{ ((p + 2)^2) * 500}\)
Simplifying further, we get:
E(p) =\(\frac{ (1000p) }{ (p^2 + 4p + 4)}\)
b) To find the elasticity at p = 9, we substitute the value of p into the elasticity equation:
E(9) =\(\frac{ (1000(9)) }{((9^2 + 4(9) + 4))}\)
= \(\frac{9000 }{ (81 + 36 + 4)}\)
=\(\frac{ 9000}{ 121}\)
= 74.38
Since the elasticity at p = 9 is greater than 1, the demand is elastic. Elasticity greater than 1 means that a percentage change in price leads to a larger percentage change in quantity demanded.
c) To find the value(s) of p for which total revenue is a maximum, we need to find the maximum of the total revenue function.
Total revenue (TR) is given by the product of price (p) and quantity demanded (q):
TR = p * q
Substituting the given demand function into the total revenue equation:
TR = \(\frac{p * ((p + 2)^2}{500}\)
=\(\frac{ (p^3 + 4p^2 + 4p) }{500}\)
To find the maximum, we take the derivative of TR with respect to p and set it equal to zero:
\(\frac{d(TR) }{dp } =\frac{3p^2 + 8p + 4}{500 }\)
Solving this equation for p will give us the value(s) of p for which total revenue is a maximum.
Unfortunately, the equation is not factorable, so we can use numerical methods such as graphing or approximation techniques to find the value(s) of p for which total revenue is a maximum.
In summary, the equation for the elasticity is E(p) = \(\frac{1000p}{p^2 + 4p + 4}\). The elasticity at p = 9 is approximately 74.38, indicating elastic demand. To find the value(s) of p for which total revenue is a maximum, further calculations or approximation methods are needed.
for more such question on elasticity visit
https://brainly.com/question/14274996
#SPJ8
1. Let the distribution of X be the normal distribution N (μ, σ2) and let Y = aX + b. Prove that Y is distributed as N (aμ + b, a2σ2).
2. Let X and Y be two independent random variables with E|X| < [infinity], E|Y| < [infinity] and E|XY| < [infinity]. Prove that E[XY] = E[X]E[Y].
Answers
1 Y is distributed as N(aμ + b, a^2σ^2), as desired.
2 We have shown that under these conditions, E[XY] = E[X]E[Y].
To prove that Y is distributed as N(aμ + b, a^2σ^2), we need to show that the mean and variance of Y match those of a normal distribution with parameters aμ + b and a^2σ^2, respectively.
First, let's find the mean of Y:
E(Y) = E(aX + b) = aE(X) + b = aμ + b
Next, let's find the variance of Y:
Var(Y) = Var(aX + b) = a^2Var(X) = a^2σ^2
Therefore, Y is distributed as N(aμ + b, a^2σ^2), as desired.
We can use the definition of covariance to prove that E[XY] = E[X]E[Y]. By the properties of expected value, we know that:
E[XY] = ∫∫ xy f(x,y) dxdy
where f(x,y) is the joint probability density function of X and Y.
Then, we can use the fact that X and Y are independent to simplify the expression:
E[XY] = ∫∫ xy f(x) f(y) dxdy
= ∫ x f(x) dx ∫ y f(y) dy
= E[X]E[Y]
where f(x) and f(y) are the marginal probability density functions of X and Y, respectively.
Therefore, we have shown that under these conditions, E[XY] = E[X]E[Y].
Learn more about distributed here:
https://brainly.com/question/29664127
#SPJ11
Whats the answer and how do i show work

Answers
The measure of <1 is 147 degree.
Given:
m∠2 = 12x - 15
m∠7 = 3x + 21
Since angles 2 and 7 are alternate Exterior angles, they are congruent.
So, 12x - 15 = 3x + 21
12x - 3x = 21 + 15
9x = 36
x = 4
So, <2 = 12x - 15= 48 - 15 = 33
Now, <1 + <2 = 180 (Linear Pair)
<1 + 33 = 180
<1 = 147 degree
Thus, the measure of <1 is 147 degree.
Learn more about Parallel line here:
https://brainly.com/question/16701300
#SPJ1
You are trying to build a logistic regression classifier which predicts whether the price of a house is less than 100K USD (class 0: cheap house) or greater than or equal to 100K USD (class 1: expensive house). The training examples given to you have two features: the depth and the frontage of the house and the associated class (0 or 1) for each training example. Assume that the price of a house is linearly dependent upon the area of the house. How would you make logistic regression work in this case? Write down the full hypothesis. (8 points)
Answers
To make logistic regression work in this case, we would need to formulate the hypothesis and apply it to the given training examples.
The hypothesis for logistic regression can be written as follows:
hθ(x) = g(θ^T * x)
Where:
- hθ(x) is the predicted probability that the house is expensive (class 1) given the features x.
- θ is the vector of coefficients that we want to estimate.
- x is the vector of features, in this case, the depth and frontage of the house.
The function g(z) is the sigmoid function, which maps any real-valued number to a value between 0 and 1. It is defined as follows:
g(z) = 1 / (1 + e^(-z))
To apply this hypothesis to the training examples, we would calculate the predicted probabilities for each example and compare them to the actual class labels. We can then use a cost function, such as the cross-entropy loss function, to measure the error between the predicted probabilities and the actual class labels. The goal is to find the values of θ that minimize this error.
By using an optimization algorithm, such as gradient descent, we can iteratively update the values of θ to minimize the cost function and find the optimal parameters for our logistic regression model.
Overall, the full hypothesis for logistic regression in this case is:
hθ(x) = g(θ₀ + θ₁ * depth + θ₂ * frontage)
Where θ₀, θ₁, and θ₂ are the coefficients that we need to estimate.
Learn more about the logistic regression here: https://brainly.com/question/27785169
#SPJ11
what do you think of france
Answers
Answer:
Baguette is very important
Step-by-step explanation:
they don't have bidet but baguette
Answer:
honestly i think its a pretty country, its pretty nice and wish i could go.
Step-by-step explanation:
What is force? O Push O Pull O Neither O Both
Answers
Answer:
Both
Step-by-step explanation:
both???????????????????????????
Seven years ago, Richard was 2/5 his father's age. Richard's father is now 47 years old. How old is Richard now?
Answers
Answer:
23
Step-by-step explanation:
seven years ago his father is 40yrs old and Richard is 16 so add seven for his present age it will be 23
Answer:
18-19
Step-by-step explanation: