Answers
Answer:
4(7+y) and 4·7+4·y
Step-by-step explanation:
4(7+y)= 28+4y
4·7+4·y= 28+4y
Related Questions
I need help on this one to sorry
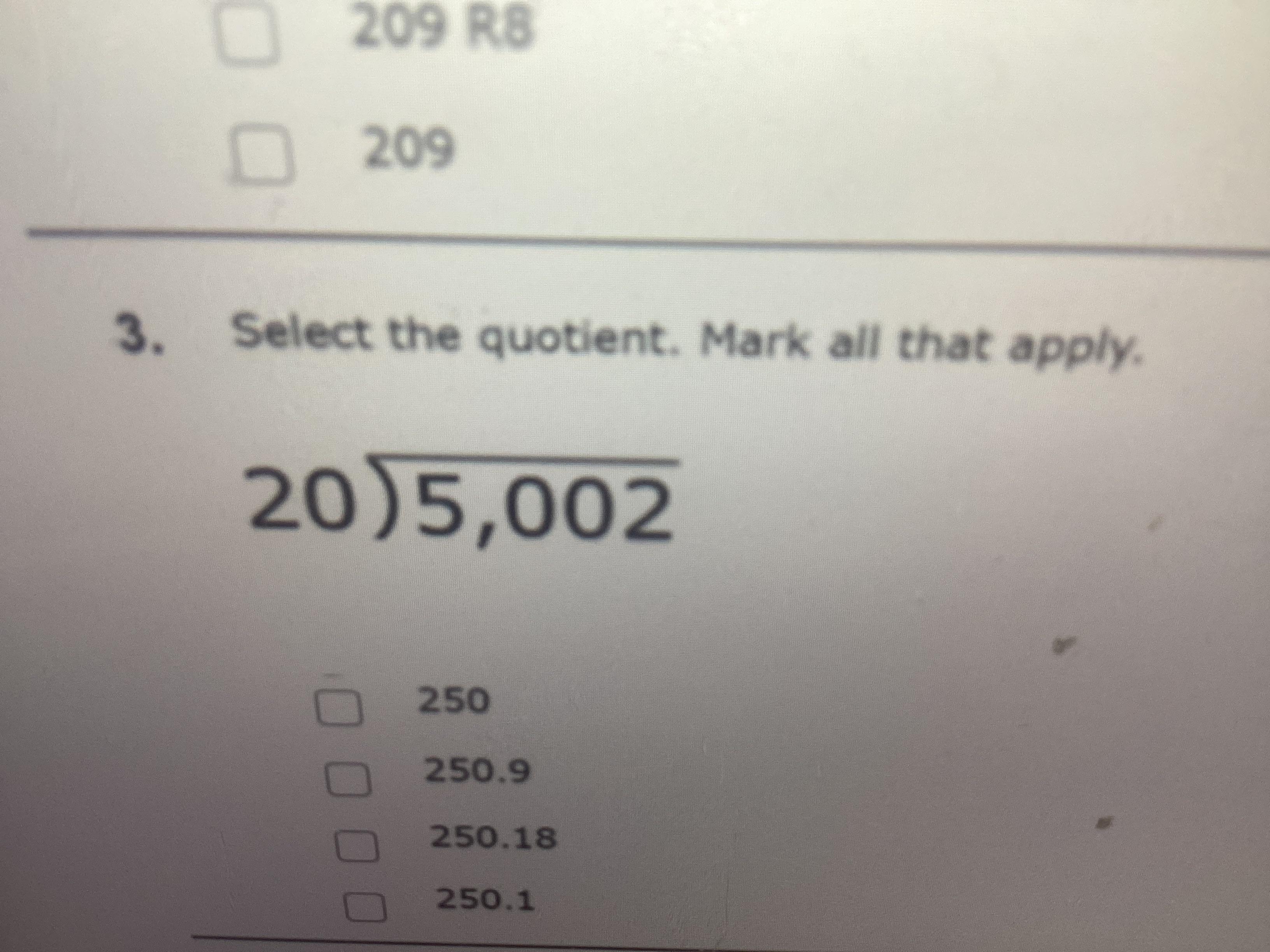
Answers
Answer:
250 and 250.1
Answer:
250.1
Step-by-step explanation:
5002 divided by 20 equals 250.1
What are the unknown angles?

Answers
A= 53°
B= 53°
C=127°
Explanation:
To find angle a, it is the same as the 53° angle given because they are corresponding angles. (Same place but on different lines)
To find angle b, we know that it is across from angle a. These types of angles are called alternate interior angles and they are always equal just like corresponding angles. So, therefore, angle b must equal angle a which is 53°.
To find angle c we know that a straight line equals 180°. Subtract the known 53 from 180 to figure out the degree of angle c.
180-53=127
Angle c=127°
You can always check your answer by making sure the line adds up to 180°
b is 53
c is 127
Select the correct answer. What is this expression in simplified form? √32×5√2
the square root of 32 multiplied by 5 to square root of 2
\( \sqrt{32 \times 5 \sqrt{2} } \)
Answers
I'm not sure but I think it's the right answer.
15.0424123723
Answer:
15.04
Step-by-step explanation:
What is an equation of the line that passes through the points (0, -2) and (6,6)
Answers
Answer:
y= 4/3x -2 or y=1\(\frac{1}{3}\) -2
Step-by-step explanation:
PLEASE PLEASE HELP Solve and explain the method you chose to use (distributive property, FOIL, multiplying special cases): (c+3)^2
Answers
After solving (c+3)², the procedure is an illustration of the distributive property of equations, and c = -3.
What is equations?Perhaps the most basic form has just been assumed to represent the fraction with the least process. How or when to decide mostly on fundamental form. Look for components that are present in both the denominator and the numerator. Sometimes it is possible to determine if a fractional integer is a power of two.
A algebraic theorem is a statement with two equal sides and an equal sign in the center. The degrees earned by each variable are stated in descending order, similar to an equation's general form. A linear equation has the formula x + b = 0. A three distinct linear function has the general form x + b y + c = 0. (or something similar). Mathematics can be categorized as identities or conditioned equations.
given:
\(( c+ 3 ) ^ 2\)
= by using formulas of \(( a+ b ) ^2\)
by distributive property
\(c^2 + 3^2 + 6c\)
\(= c^2 + 9 + 6c\)
\(c^2 + 3c + 3c + 9 = 0\)
= (c + 3 )(c+ 3)
c = -3
After solving (c+3)², the procedure is an illustration of the distributive property of equations, and c = -3.
To know more about equation visit:
brainly.com/question/649785
#SPJ1
The radius of a circle is 16 meters. What is that circle’s area?
Answers
Answer:
256pi or 804.248 m sq
Step-by-step explanation:
the formula for the area of a circle is pi*r^2 and we know the radius. so the area is pi*16^2=256pi. if you want the decimal answer it's around 804.248
Which line segments have a positive slope PLS FAST!! THANKS!!

Answers
a-b
it’s the ones where it’s pointing up to the right!
what's 6 to the power of 900?
Answers
Answer:
5400
Step-by-step explanation:
6x900 =5400 this is the correct answer
what is -2 x 3 i do not understand this and this is my last problem
Answers
Answer:
-6
Step-by-step explanation:
if they were both positive numbers, it would be 6. But when you multiply a negative by a positive, the answer is negative.
Answer:
-6
Step-by-step explanation:
When you multiply a positive number by another positive number, you will always get a positive number as your answer. Same thing for negative. If you multiply a negative by a negative, you will always get a positive. However, when you multiply a negative by a positive, you will always get a negative number.
Since you know this, you can multiply 2 by 3, which is 6. Because 2 is negative and 3 is positive, you know that the answer must be negative. Therefore, you add the negative symbol to 6, giving you -6.
I hope this isn't too confusing. Please let me know if you have any more questions. Good luck!
Solve with substitution
X=-3y-8
X-2y=-3

Answers
Answer:
x=-5, y=-1
Step-by-step explanation:
Please explain your answer to the question in the picture with steps

Answers
Answer:
x = 31.2
Step-by-step explanation:
You want the solution to the proportion 12/x = 5/13.
Rational equationYou can eliminate the fractions by multiplying this equation by the least common denominator. That value is 13x, the product of these denominators. Multiplying by 13x, we have ...
\(\dfrac{12}{x}\times13x=\dfrac{5}{13}\times13x\\\\\\12\cdot13=5\cdot x\qquad\text{simplified}\)
Now, the value of x is found by dividing both sides by its coefficient.
\(\dfrac{12\cdot13}{5}=\dfrac{5x}{5}\\\\\\\dfrac{156}{5}=x\\\\\boxed{31.2=x}\)
__
Additional comment
The first step we did, multiplying by 13x, is also sometimes called "cross multiplication." The result of that step is that each numerator is multiplied by the opposite denominator.
Multiplying both sides of the equation by the same value (13x) is supported by the multiplication property of equality. The term "cross multiplication" is descriptive of the result, but is not a recognized property of equality. It is a good idea to keep the math operations you do grounded in the properties of equality.
You will notice that the steps we did were "multiply by 13x" and "divide by 5". These can be done at once by "multiply by 13x/5". Of course, that operation is done to both sides of the equation.
Any proportion can be written 4 ways:
\(\dfrac{12}{x}=\dfrac{5}{13}\qquad\dfrac{x}{12}=\dfrac{13}{5}\qquad\dfrac{x}{13}=\dfrac{12}{5}\qquad\dfrac{13}{x}=\dfrac{5}{12}\)
These can be thought of as "upside down" and "sideways." We like the versions with the variable on top of a fraction, because the solution to that is simply multiplication by the variable's denominator.
<95141404393>
Which of the following is not a solution of the equation y=3x-4?
A. 2,2
B. 0,-4
C. 4,8
D. -1,-1
Answers
2 = 3(2) - 4, true
-4 = 3(0) - 4, true
8 = 3(4) - 4, true
-1 = 3(-1) - 4, false
Solution: D
2x+3≤x−5 solve for x
Answers
Answer:
x≤−8
Step-by-step explanation:
2x+3≤x−5
Step 1: Subtract x from both sides.
2x+3−x≤x−5−x
x+3≤−5
Step 2: Subtract 3 from both sides.
x+3−3≤−5−3
Answer is
x≤−8
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8
What are the dependent and independent
variables?
Answers
Answer:
The dependent variable depends on the value of some other number also known as the independent variable. Another way to put it is the dependent variable is the output value and the independent variable is the input value. So for y=x+3, when you input x=2, the output is y = 5.
The images are some examples.


11. Check for Reasonableness Santiago wants to display categorical data
in a circle graph. He divides the circle graph into 5 equal sections because
the data set has 5 groups. Do you agree? Justify your answer,
Answers
Answer: Not necessarily. Dividing the pie chart into 5 equal sections might be a way to display categorical data if the number of categories is 5. However, dividing it into 5 sections might not be the best way to display the data if the number of categories is different than 5 or if any category has a significantly higher or lower proportion than the others. In this case, it may be more appropriate to use a different scale to display the correct ratio. It is important to consider data distribution and visualization clarity before choosing how to display categorical data.
If a driver uses of a tank of gas every day, what fraction of a tank will he use in a) 3 days? b) 1 week?
Answers
Answer:
Step-by-step explanation:
a) If a driver uses a full tank of gas every day, the fraction of a tank he will use in 3 days is 3/1, or 3/1 of a tank.
b) If a driver uses a full tank of gas every day, the fraction of a tank he will use in 1 week is 7/1, or 7/1 of a tank.
It's worth noting that tanks of gas come in different sizes, so the amount of gas consumed in a day, week, or any other period of time will depend on the size of the tank, and the consumption of the car, so this answer is based on the assumption that a full tank is used every day.
1 year insurance policy covering its equipment was purchased for 6,144. The date purchased was June 14 but it doesn't go into effect until June 16th, How much is paid for that
month?
Year?
Answers
1 year insurance policy covering its equipment was purchased for 6,144. The date purchased was June 14 but it doesn't go into effect until June 16th, the amount paid for the month of June is approximately $252.75, and the amount paid for the entire year is approximately $6,144.
To calculate the amount paid for the month and the year, we need to consider the number of days covered by the insurance policy. Let's break it down step by step:
Step 1: Determine the number of days covered in June.
Since the policy doesn't go into effect until June 16th, there are 15 days remaining in June that will be covered by the insurance policy.
Step 2: Calculate the daily rate.
To find the daily rate, we divide the total cost of the insurance policy by the number of days in a year:
Daily rate = 6,144 / 365
Step 3: Calculate the amount paid for June.
The amount paid for June can be found by multiplying the daily rate by the number of days covered:
Amount paid for June = Daily rate * Number of days covered in June
Step 4: Calculate the amount paid for the year.
To calculate the amount paid for the year, we simply multiply the daily rate by 365 (the total number of days in a year):
Amount paid for the year = Daily rate * 365
Now let's perform the calculations:
Step 2: Daily rate
Daily rate = 6,144 / 365 ≈ 16.85 (rounded to two decimal places)
Step 3: Amount paid for June
Amount paid for June = 16.85 * 15 ≈ 252.75 (rounded to two decimal places)
Step 4: Amount paid for the year
Amount paid for the year = 16.85 * 365 ≈ 6,144 (rounded to two decimal places)
For more such information on: amount
https://brainly.com/question/25720319
#SPJ8
Jan plans to tell two people each day and will ask that person to tell two other people each day through the day of the opening, and so on. Assume that each new person who hears about the soft opening is also asked to tell two other people each day through the day of the opening and that each one starts the process of telling their friends on the day after he or she first hears. When should Jan begin telling others about the soft opening in order to have at least 700 people know about it by the day it occurs?

Answers
Explanation:
From the given question, we can sketch the pattern observed
The figure above helps show how the number of people increases
Initially, Jan tells 2 more people, then the two people tell two more people, then they also tell two more people
Thus
we can see that the model is given by
\(\begin{gathered} (2)^n \\ where\text{ n is the number of days} \end{gathered}\)In order to have at least 700 (it also means a minimum of 700), we will have the equation
\(2^n\ge700\)We then solve for n
Taking the log of both sides
\(n\text{ }log2\ge log700\)\(n\ge\frac{log700}{log2}\)So that
\(\begin{gathered} n\ge\frac{2.845}{0.301} \\ \\ n\ge9.451 \end{gathered}\)So, the number of days will be at least 10 days (Rounded to the nearest whole day )

I'm not good at math, but i really, really need help, what's the exact steps of 2+1(-1-3)?
Answers
Answer:
Step-by-step explanation:
2+1(-1-3)
= 2+1[-(1+3)]
= 2+1(-4)
= 2+(-4)
=-(4-2)
=-2
Answer:
i think it's like this
2-1-3
=-2
create a matrix. use a graphing calculator to solve the system using the rref function.
-11x-4y=36
5x+5y=-10
Answers
Answer:
\(x=-\dfrac{44}{7}\)
\(y=\dfrac{58}{7}\)
Step-by-step explanation:
Arrange the equations so that all the variables are in columns (x as the first column, y as the second, equals a number as the third):
-11x - 4y = 36
5x + 5y = -10
Define and edit Matrix A. We need a 3 x 2 matrix. Input the coefficients and constant:
\(\left[\begin{array}{ccc}-11&-4&36\\5&5&-10\end{array}\right]\)
Find rref function, enter matrix A: rref([A]) (press enter)
This gives you:
\(\left[\begin{array}{ccc}1&0&-\frac{44}{7}\\0&1&\frac{58}{7}\end{array}\right]\)
which means:
\(x=-\dfrac{44}{7}\)
\(y=\dfrac{58}{7}\)
Find sin(2x), cos(2x), and tan(2x) from the given information.
sin(x) = \(-\frac{3}{5}\) for \(\frac{3\pi }{2}\) < x < 2
Answers
I assume 3π/2 < x < 2π, so that x is in the 4th quadrant. For angles x terminating in Q4, we have sin(x) < 0 and cos(x) > 0, so tan(x) = sin(x)/cos(x) < 0.
This means that, using the Pythagorean identity,
cos(x) = + √(1 - sin²(x)) = 4/5
tan(x) = (-3/5) / (4/5) = -3/4
Recall the double angle identities:
sin(2x) = 2 sin(x) cos(x) = 2 (-3/5) (4/5) = -24/25
cos(2x) = 2 cos²(x) - 1 = 2 (4/5)² - 1 = 7/25
tan(2x) = 2 tan(x) / (1 - tan²(x)) = 2 (-3/4) / (1 - (-3/4)²) = -24/7
Would someone help ? Thank you ! :)

Answers
Answer:
Transitive Property of Congruence
Step-by-step explanation:
If angle 1 is = to angle 2 and angle 2 = angle 3, then angle 1 has to equal angle 3.
The solution of the equation 3x + 4 =1 is a) 1 b) 0 c) -1 d) 2
Answers
Hello!
3x + 4 = 1
3x + 4 - 4 = 1 - 4
3x = -3
3x/3 = -3/3
x = -1
The solution of the equation 3x + 4 = 1 is -1.
The answer is:
C) x = -1
Work/explanation:
To solve this equation, I subtract 4 from each side:
\(\sf{3x+4=1}\)
Subtract :
\(\sf{3x=-3}\)
Divide each side by 3:
\(\sf{x=-1}\)
Hence, C is correct.
Suppose that P(n) is a propositional function. Determine for which improper subset of the domain of n the statement P(n) must be true if a) P(0) is true; for all nonnegative integers n, if P(n) is true, then P(n 2) is true. b) P(0) and P(1) are true; for all nonnegative integers n, if P(n) and P(n 1) are true, then P(n 2) is true
Answers
Answer:
a) P(n) is true for all 'n' in the set ; { 0,2,4,6,8 ….. }
b) P(n) is true for all 'n' in the set ; { 0,1,2,3,4,5 ............ }
Step-by-step explanation:
a) As P(0) is true
we will assume that
P(2) is trueP(4) is true P(6) is truethis simply means that ; P(n) is true for all 'n' in the set
{ 0,2,4,6,8 ….. }
b) since P(0) and P(1) are true
we will assume that
P( 0+2 ) = P(2) is truealso P(1) and P(2) are true
we will assume that
P(1+2) = P(3) is trueAlso from the previous answers it can be seen that P(2) + P(3) is true
we will assume
P(2+2) = P(4) is trueThis simply means that P(n) is true for all 'n' in the set
{ 0,1,2,3,4,5 ............ }
A commuter train travels 51 in minutes. What is its speed in 26 per hour?
Answers
The speed of the commuter train in kilometre per hour is 30.59 kilometres per hour
How to determine the speed in kilometres per hour?The given parameters are
Distance = 26 kilometres
Time = 51 minutes
Convert the number of minutes to hour
So, we have
Time = 51/60 hour
The speed of the commuter train in kilometre per hour is calculated as
Speed = Distance/Time
So, we have
Speed = 26 kilometres/(51/60 hour)
Evaluate the quotient
Speed = 30.59 kilometres per hour
Hence, the speed of the commuter train in kilometre per hour is 30.59 kilometres per hour
Read more about speed at
https://brainly.com/question/6504879
#SPJ1
Which is the graph of g(x) = 2^(x – 1) + 3?
Answers
Hope this helps!

Solve the equation 2/3x - 1/5x = x - 1
Answers
Answer:
To solve the equation:
2/3x - 1/5x = x - 1
First, we need to find a common denominator for 2/3 and 1/5, which is 15. So we can rewrite the equation as:
(10/15)x - (3/15)x = 15/15 x - 1
Simplifying the left side:
(7/15)x = 15/15 x - 1
Multiplying both sides by 15:
7x = 15x - 15
Subtracting 7x from both sides:
-8x = -15
Dividing both sides by -8:
x = 15/8 or 1.875
Therefore, the solution to the equation is x = 1.875.
hich linear function has the steepest slope?
y = negative 8 x + 5
y minus 9 = negative 2 (x + 1)
y = 7 x minus 3
y + 2 = 6 (x + 10)
Answers
The function with the steepest slope is \(y = 7x - 3\).
The correct answer is C.
The linear function with the steepest slope is the one with the highest absolute value for the coefficient of x.
Let's compare the coefficients of x in each of the given functions:
\(y = -8x + 5\)
Slope: -8
\(y - 9 = -2(x + 1)\)
Simplifying, we get \(y - 9 = -2x - 2\)
Rearranging, we have \(y = -2x + 7\)
Slope: -2
\(y = 7x - 3\)
Slope: 7
\(y + 2 = 6(x + 10)\)
Simplifying, we get \(y + 2 = 6x + 60\)
Rearranging, we have \(y = 6x + 58\)
Slope: 6
Therefore, the steepest slope is the \(y = 7x - 3\).
For such more questions on steepest slope
https://brainly.com/question/10726891
#SPJ8
IS THIS RIGHT? (28 points easy!!)

Answers
Step-by-step explanation:
yes, the step is correct.
a² = cx | multiply by c
ca² = c²x
I am just not sure how that simplified the equation.
what do you want to achieve ? what's the goal here ?
to solve the equation for x it would be to divide both sides by c, which gives
a²/c = x
